非定常流场的分区计算方法
傅翔, 李高华, 王福新
(上海交通大学 航空航天学院,上海 200240)
0 引言
计算流体力学方法即指用数值手段来求解描述流场运动的N-S方程,它是获取流场详细数据的最简单直接的方法,被广泛用于航空航天设计、汽车外形设计、化学工业处理、生物医学工程以及仿生学研究等领域[1]。
计算流体力学方法起源于20世初60年代,Lax等人提出了N-S方程差分逼近的稳定性理论[2],为计算流体力学发展打下了良好的基础。1971年,美国的弗鲁姆和哈洛利用计算机第一次成功的计算出了二维长方柱体的绕流,并对卡门涡街的形成做了细致的分析[3]。此后,随着一大批先进数值计算理论的提出[4,5]以及电子计算机的快速发展,计算流体力学方法进入了飞速发展的时代。到20世纪80年代之后,计算流体力学方法在网格生成、方程离散、湍流理论以及迭代方法等方面已经基本完善,在科学研究以及工程应用方面的应用也越来越多[6]。
即便计算流体力学方法在最近几十年取得了巨大的进步,但依然还存在着一个很大的缺点,就是需要耗费非常多的计算时间。这一缺点在面对复杂的非定常流场计算时得到了放大。以计算旋翼非定常流场为例,通常计算一个完整的旋转周期就需要几个月的时间[7],这还是在采用大规模并行处理的前提下。
为了减少计算时间,提高研究效率,本文基于速度-涡形式的N-S方程,提出了新的分区计算方法。该方法将整个流场计算域分为势流域、边界层域和N-S方程域3个区域,由于势流域占据了绝大部分流场且不需要求解涡量输运方程,所以能够在保证精度的情况下极大的减少计算时间。进一步的,用该方法计算了震荡翼型所产生的非定常流场,计算结果清晰的显示了前缘涡和尾缘涡的脱落过程。
1 数值计算方法
1.1 基本控制方程
流体的运动是由N-S方程决定的,N-S方程可以通过变换写成很多种形式,比如速度-压力形式、速度-压力形式以及涡量-流函数形式等。其中速度-涡形式的N-S方程可表示为[8]式(1)—式(3)。

(1)

(2)
(3)
其中v和ω分别是速度和涡量,ν是流体的动粘性系数。
式(1)和式(2)是描述涡量和速度关系的涡量运动学方程。式(3)为涡量传输方程,它描述了流场中涡量的演化方式,即流场中的涡量变化率是由涡的传输、拉伸旋转以及耗散决定的。联立涡量传输方程和式(1)、式(2)即可求得流场中每个时刻的涡量分布。
1.2 非定常气动力计算方法
由于速度-涡形式的N-S方程没有出现压力项,所以直接采用涡量矩定理[9]进行面积分来计算物体所受到的非定常气动力为式(4)。
∭RSvdR
(4)
其中ρ是流体密度,r是矢径。式(4)表明物体所受气动力与流场内所有涡量的涡量矩的时间变化率相关,即只要知道流场内的涡量分布,就可以得到相应的气动力。
将式(4)分别向x和y方向投影即可得物体的阻力和升力为式(5)、(6)。
∭RSvdR
(5)

(6)
1.3 计算步骤
分区计算方法的核心在于将整个流场分为势流域、边界层域和N-S方程域。在每个时刻,该方法将涡量为0的流场区域定义为势流域,将物体表面的区域定义为边界层域,将脱落涡区域设为N-S方程域。
由于势流域内不需要求解涡量输运方程而且势流域占据了绝大部分流场,所以这样的设置能够极大的减少计算量。
分区计算方法的具体求解步骤如下:
1)在n+1时刻,更新物体边界上的速度。
2)设置迭代步数k=1。
3)在N-S方程域内求解涡量输运方程,在边界层域内求解边界层方程,得到n+1时刻流体内部的涡量预估值。
4)利用第三步求出的n+1时刻流体内部的涡量预估值和物体边界上的速度求出n+1时刻物体边界上的涡量预估值。
5)更新迭代步数,k=k+1。
6)重复第三步到第五步,直到算出的n+1时刻物体边界上的涡量预估值满足收敛准则。
7)用式(2)求出全域的速度场。
8)利用式(5)和式(6)计算阻力和升力。
9)回到第一步,进入下一个时刻。
3 计算结果分析
用该方法计算了俯仰震荡翼型绕流流场。翼型为NACA0012对称翼型,雷诺数设为1×106。用商业软件生成绕翼型的O型网格,网格外边界的半径为翼型长度的25倍,整个网格及翼型附近的网格结构,如图1所示。

(a)及翼型附近网格(b)示意图
图1 整个网格
为了避免每个时间步都要生成网格,故在翼型运动的过程中,网格跟随翼型一起运动。将转动轴取在四分之一弦长处,翼型攻角的变化规律为式(7)。
(7)
其中αm是翼型的最大攻角,k是缩减频率,c是翼型弦长,U∞是无穷处来流速度。
设f为震荡频率,则k和f存在以下关系式为式(8)。
(8)
为了得到强烈的非定常流场,将翼型最大攻角设为αm=20°,将缩减频率设为k=2.9。
由于在翼型震荡的过程中,涡量主要集中在翼型背风方向,所以将翼型背风附近区域设置为N-S方程域,将翼型迎风附近区域设置为边界层域,将其它部分设为势流域,如图2所示。
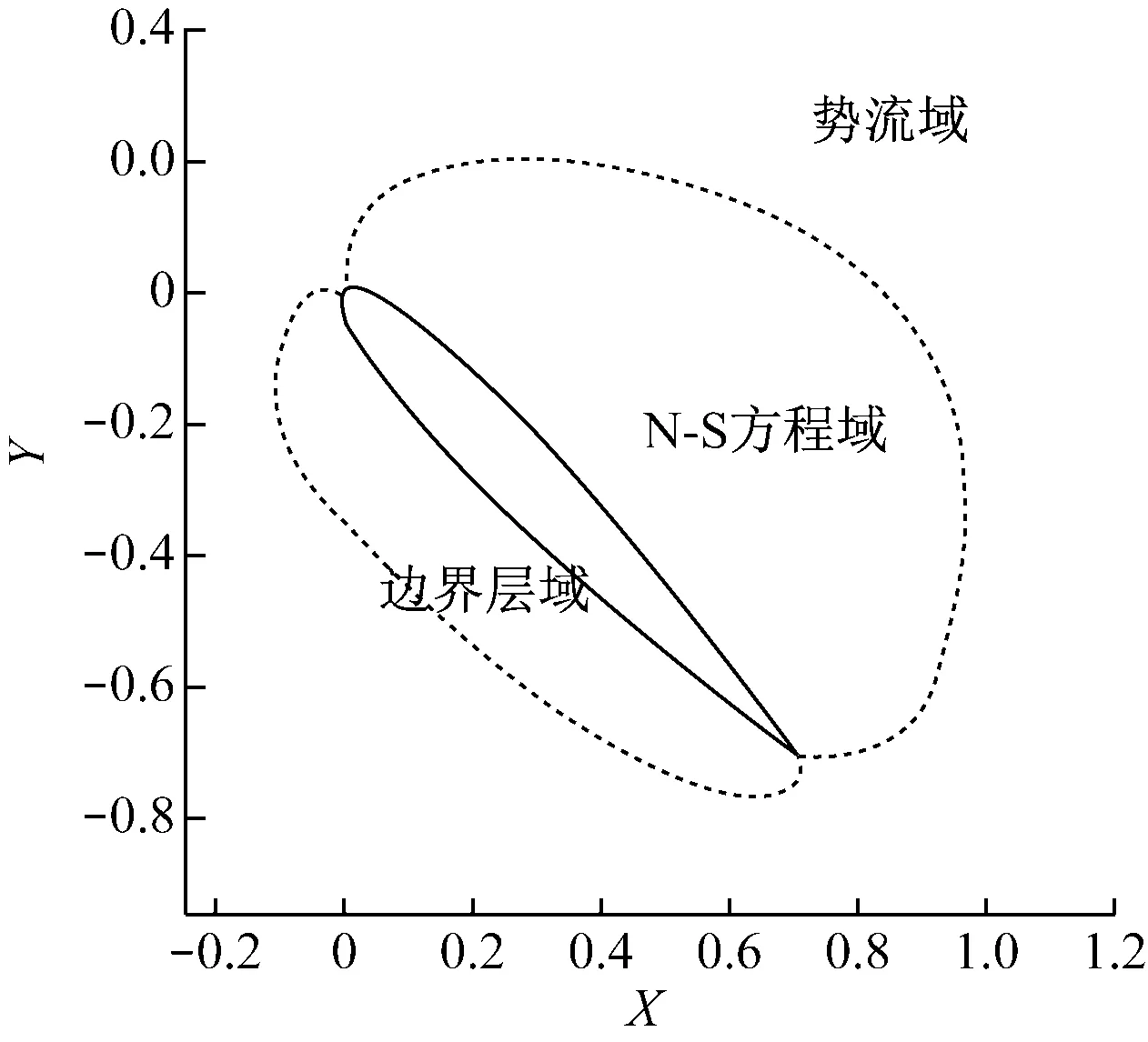
图2 势流域、边界层域及N-S方程域示意图
分别用本文提出的分区计算方法和计算流体力学商业软件Fluent计算一个周期T的震荡翼型非定常流场,将计算所耗用时间,如表1所示。
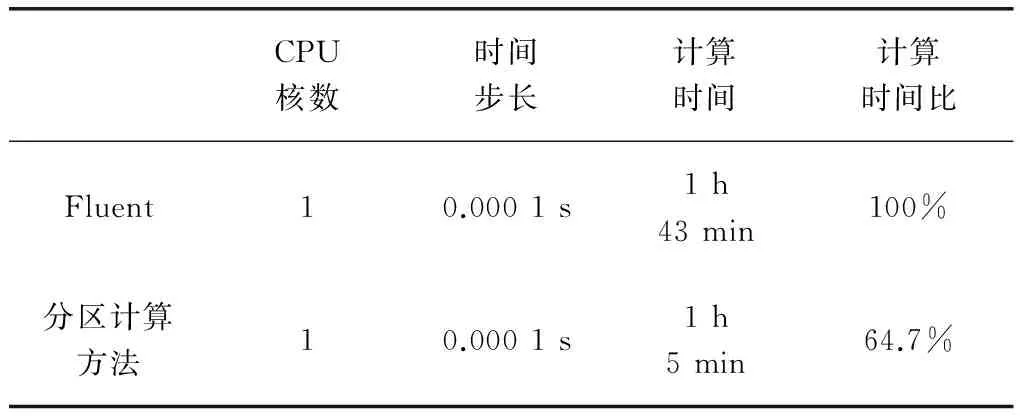
表1 一个震荡周期T所需要的计算时间
由表1可知,在相同的计算条件下,分区计算方法比Fluent能够减少三分之一的计算时间,大大提高了计算效率。
分区计算方法计算出的一个震荡周期内翼型附近的瞬时涡量云图,如图3所示。

(a)t=0T(b)t=0.143T(c)t=0.286T(d)t=0.429T(e)t=0.571T(f)t=0.714T(g)t=0.857T(h)t=T
图3 一个震荡周期内翼型附近的瞬时涡量云图
从图3中可以看出分区计算方法准确的计算出了前缘涡和尾缘涡的脱落过程。在俯仰运动的初始时刻(t=0T),翼型正在由0攻角位置向上抬起,一个逆时针方向的尾缘涡逐渐在翼型尾缘的右后方形成,同时,一个顺时针方向的前缘涡也在翼型上表面形成。当t=0.143T时,尾缘涡吸收了从尾缘脱落的涡量并逐渐变大,而前缘涡则保持了原来的大小并沿着翼型表面向下游运动。当t=0.286T时,翼型的攻角几乎已经达到最大,尾缘涡开始从尾缘脱落,前缘涡则运动到翼型尾缘位置。当t=0.429T时,翼型开始向下低头,已脱落的尾缘涡顺着来流向下游运动,而前缘涡则与新生成的顺时针方向的尾缘涡融合在一起。当t=0.571T时,新生成的尾缘涡逐渐变大,同时一个新的逆时针方向的前缘涡又在翼型下表面形成。当t=0.714T时,翼型几乎已达到负的最大攻角,新生成的尾缘涡继续从尾缘吸收涡量并逐渐变大,而新生成的前缘涡则沿着翼型下表面向下游运动。当t=0.857T时,翼型又开始做抬头运动,新生成的尾缘涡从尾缘处脱落并顺着来流向下游运动。如此反复,就形成了以对涡形式存在的反卡门涡街。由于设置的缩减频率比较高,流动的不稳定性也比较大,所以脱落的涡街并不是水平的,而是向上方偏离的。
翼型在一个震荡周期内所受到的升力和阻力,如图4所示。
从图4中可以看出,翼型所受的升力在翼型抬头的过程中缓慢上升,至尾缘涡从尾缘脱落的时刻达到最大。在此之后,升力开始逐渐下降,并在新生尾缘涡从尾缘脱落的时刻达到负的最大值。最后,由于翼型重新开始抬头运动,升力又逐渐上升。而翼型所受到的非定常阻力均为负值且呈现出正弦函数分布,即说明了在高频率震荡情况下,翼型受到的是推力。这与鱼类通过快速摆动尾巴向前游动现象吻合。
4 总结
本文基于涡-速度形式的N-S方程,提出一种分区计算非定常流场的方法,将整个计算流场划分为势流域、边界层域以及N-S方程域三个部分。利用该方法计算了高频俯仰震荡翼型的非定常流场,发现该方法比商业计算软件Fluent节省近三分之一的计算时间。此外,利用该方法计算出的非定常流场,对高频震荡翼型反卡门涡街的形成以及非定常力的演化过程进行了详细的研究。
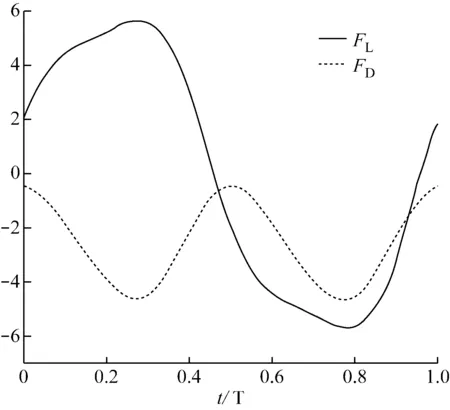
图4 一个震荡周期内翼型的升力和阻力(N)
[1] Versteeg H K, Malalasekera W. An introduction to computational fluid dynamics-The finite volume method[M]. Singapore: World Scientific, 1995.
[2] Reddy S C, Trefethen L N. Lax-stability of fully discrete spectral methods via stability regions and pseudo-eigenvalues [J]. Computer Methods in Applied Mechanics & Engineering, 1990, 80(1-3):147-164.
[3] Anderson, John David. Computational fluid dynamics: the basics with applications[M]. Beijing: Tsinghua Press, 2002.
[4] Blazek J, Blazek J. Computational Fluid Dynamics: Principles and Applications, Second Edition[J]. Computational Fluid Dynamics Principles & Applications, 2001, 55(2):1-4.
[5] Oberkampf W L, Trucano T G. Verification and validation in computational fluid dynamics[J]. Progress in Aerospace Sciences, 2002, 38(3):209-272.
[6] Al-Baali A G, Farid M M. Fundamentals of Computational Fluid Dynamics[J]. 2002, 55(4):33-44.
[7] Gupta R, Biswas A. Computational fluid dynamics analysis of a twisted three-bladed H-Darrieus rotor[J]. Journal of Renewable & Sustainable Energy, 2010, 2(4):691-694.
[8] Davies C, Carpenter P W. A Novel Velocity-Vorticity Formulation of the Navier-Stokes Equations with Applications to Boundary Layer Disturbance Evolution[J]. Journal of Computational Physics, 2001, 172(1):119-165.
[9] Wu J C. Theory for aerodynamic force and moment in viscous flows[J]. AIAA Journal, 1981, 19(4): 432-441.

