K均值聚类-粒子群优化多目标定位算法

廖延娜，李梦君，张婧琪

（1.西安邮电大学理学院，陕西西安710121；2.西安邮电大学电子工程学院，陕西西安710121；3.中国兵器工业第二0三研究所陕西西安710065）

随着海洋开发、国防建设和智能交通等应用领域的快速发展，多目标识别技术[1]受到越来越多的重视，同时对多目标的识别能力和分辨精度的要求日益提高[2]。目标的准确定位对于目标识别以及图像的理解与分析都起着重要的作用[3]。目标定位多应用于无人飞行器定位[4]、遥感及医学图像分析[5]、零部件识别与定位、产品检验、摄影测量和车辆识别[6]等应用中。常见的单目标定位方法，如灰度特性法[7]、hough变换法[8]、数学形态学法[9]、纹理特征分析法[10]、彩色分割法[11]等，已经被充分的研究和讨论。而对多个目标进行定位研究的内容却不多见。

针对目前多目标定位和识别的实际需要，文中提出一种K均值聚类-粒子群优化的多目标定位算法。算法以粒子群优化为核心，结合K均值聚类保持种群的多样性[12]，从而实现图片中多个目标的准确、自动定位。

1 粒子群优化算法原理

粒子群算法（ParticleSwarm Optimization，PSO）[13-14]是一种群体智能优化算法[15]：在一个D维搜索空间内，n个粒子组成的种群（粒子群）不断调整速度和位置；通过若干次迭代搜索，到达最优位置，即得到算法最优解。在迭代搜索的过程中，每个粒子跟踪比较两个极值：个体极值P_best，即单个粒子自身找到的最优解；全局极值G_best，即整个粒子群体找到的最优解；从而实现粒子个体位置与速度的更新。

粒子群算法位置与速度更新公式如下：

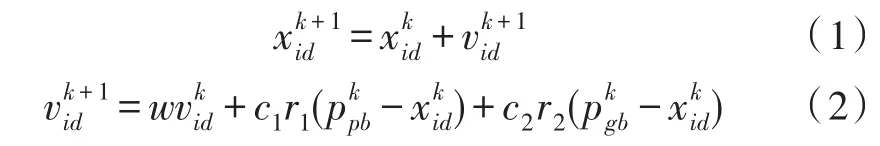
其中，wmin为最小权重；wmax为最大权重；runMax为算法的最大迭代次数；run为当前迭代次数。

2 排挤机制K均值聚类

为了保持目标粒子种群[16]的多样性，引入K均值聚类算法[17]。K均值聚类是一种以距离为判定条件的聚类算法，根据目标粒子的编码设计，定义目标粒子i与j之间的距离dij的度量函数。

为避免算法收敛缓慢或陷入局部最优解，初始质心的位置对K均值聚类算法来说十分重要。本文根据目标粒子的适应度Fitness[18]，采用基于排挤机制的初始聚类质心产生法，其思想如下：

根据粒子编码生成表示目标的粒子种群后，将种群中的n个元素按照适应度Fitness_S的大小由高到低进行排序，记为{p1,p2,…,pn}，令初始聚类质心C1=p1。

计算距离矩阵Dn×n={dij}，预设距离门限DisT，若d12＞DisT，则认为p1和p2距离甚远，可作为两个不同的初始聚类质心，即令C2=p2；反之，则认为p1和p2距离过近，舍去p2，继续比较d1i和DisT，直至选出C2=pi。

根据选出的C1=p1和C2=pi，继续考察粒子pj(j＞i)：若d1j＞DisT且dij＞DisT，则令初始聚类质心C3=pj。

以此类推，直至选出全部M个初始聚类质心。

3 K均值聚类-粒子群优化联合算法

K均值聚类-粒子群优化联合算法的思想设计为：利用K均值聚类将目标粒子种群划分为若干个子群，在每个子群中，用粒子群算法进行优化；然后再重复进行聚类、优化，直到各个目标子群得到最优解。K均值聚类-粒子群优化交错算法实现多目标定位的具体步骤如下：

Step 1：随机初始化目标种群粒子速度与位置；

Step 2：计算每个目标粒子的适应度Fitness；

Step 3：采用基于排挤机制的K均值聚类算法确定聚类质心并对种群进行分类，得到M个子群；

Step 4：根据目标粒子的适应度，确定每个子群的全局极值和个体极值，并根据粒子速度和位置更新公式对子群中的粒子进行更新；

Step 5：重新计算每个子群的质心，根据排挤机制的预设距离门限，判断是否需要重新聚类，若需要则返回Step 3，否则算法继续向下运行；

Step 6：判断是否达到粒子群算法预设的迭代次数，若达到则结束算法输出结果，若没达到则返回步骤2重新执行。

算法流程图如图1所示。

4 仿真实验

4.1 目标粒子编码设计

文中以多车牌定位为例，对多目标定位算法进行仿真了实验。粒子编码是粒子群算法重要部分。本文设计车牌目标粒子编码为4维粒子pi={Xi,Yi,Li,Wi}；该目标粒子中的各维分量分别代表车牌左上角坐标X，左上角坐标Y，车牌长L和车牌宽W。

图1 算法流程图

目标粒子编码时若不加任何限制，可能出现粒子初始位置离最优解较远，极大的影响粒子寻优的速度，并可能导致算法无法收敛。在实际应用中，监控摄像机位置相对固定，所摄图像中车牌的大小只在一定范围内变化。因此文中根据图像的大小对车牌目标粒子编码进行如下限制：

其中xmax和ymax分别代表图片的最大长和宽；l和w为实际车牌长宽参考值；a和b为相应的调整量。

4.2 目标粒子特征提取

在灰度二值化后的图像中，车牌区域在水平方向呈现有一定疏密度的黑白间隔的纹理分布，这是车牌目标粒子的一大特征。本利用多尺度滤波技术，采用一组反映不同疏密度的高斯差分滤波器L1、L2、L3对图像进行滤波，即将车牌目标粒子区域T(x,y)与滤波模板卷积：

根据车牌纹理特征空间分布的均匀性，使用Di(x,y)的标准差来表示车牌目标粒子纹理特征值σi和特征描述向量T：

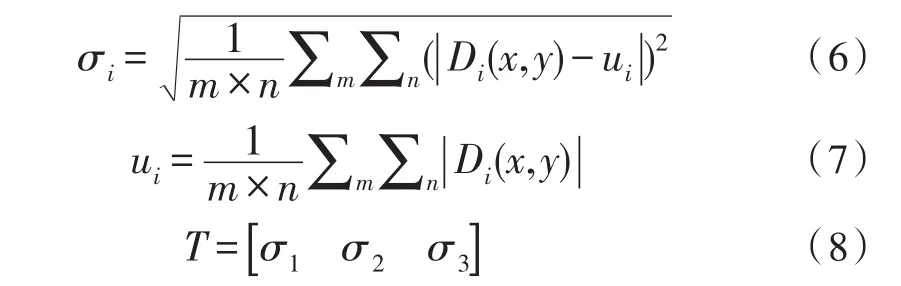
其中m、n为车牌目标粒子区域的大小。

由于车牌由各种字符组成，与其他位置相比纹理变化较剧烈，可以认为车牌目标粒子特征向量T的模越大，则越有可能是车牌目标区域。故设计适应度函数如下：

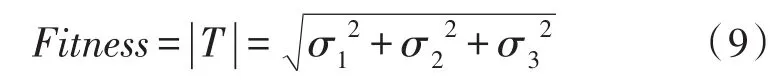
鉴于σi＞0，也可以简化设计适应度函数Fitness_S=σ1+σ2+σ3。

4.3 仿真结果

算法仿真环境为matlab2012a，仿真测试图片样本来源于在某单位停车场一个月时间范围内随机拍摄的近三百副图片，图片大小为640×300。图片拍摄时模拟固定摄像头位置，根据实际图片，设置则车牌长、宽度调整量a=32，b=8。粒子大小为50，粒子最大速度限制为vmax=[vXmaxvYmaxvLmaxvWmax]=[20 10 4 2]，wmin=0.1，wmax=0.9，学习因子c1=c2=1；粒子群算法最大迭代次数设为50。

以包含两辆车和三辆车的图片为例，图2为初始粒子种群经过聚类过后的车牌目标分布状态。

图2 聚类后车牌目标分布图

图2中不同的虚、实型线分别代表不同类的车牌目标。由图可见，通过排挤机制的K均值聚类算法能够有效将待定目标区域分类，且分布在实际目标的周围。

图3为粒子群算法中，每个子群最优全局极值，即最优目标粒子的适应度变化趋势图。

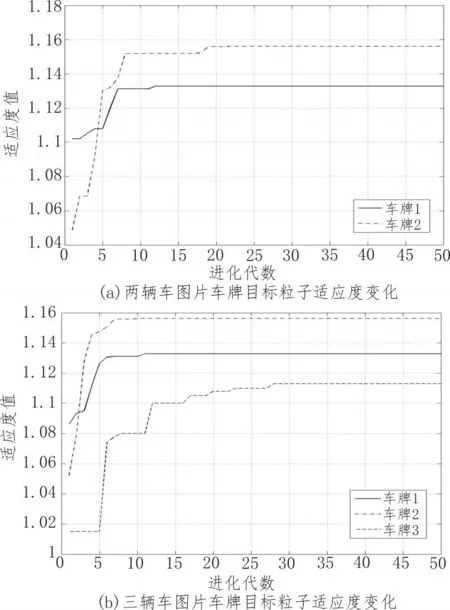
图3 车牌目标粒子适应度变化趋势

由图3可见，粒子群进化过程中，最优车牌目标粒子的适应度随进化代数增加而增大，并渐趋稳定，50代以内粒子群算法基本收敛。

图4为最终的车牌目标定位结果。可见针对包含两辆车和三辆车的图片，最终的车牌目标定位结果准确。

图4 车牌目标定位最终结果

分别以包含两辆车的100幅两车图片和包含3辆车100幅三车图片作为测试样本，重复运行50次进行测试，目标定位成功率统计结果如表1所示。

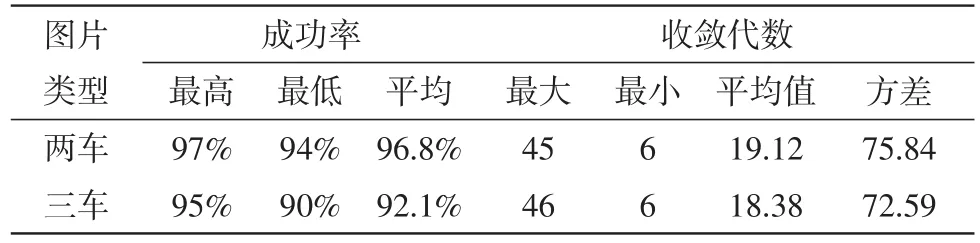
表1 多车牌定位结果统计

仿真实验统计结果表明：两车图片的车牌目标定位的平均成功率在96.8%；随着图片复杂性的增加，三车图片的车牌目标定位成功率略低于两车图片。粒子群算法最快6代内即达到收敛，最慢46代达到收敛。为了更好的说明算法的收敛代数分布，图5对粒子群算法收敛代数进行了分段统计。

图5 粒子群算法收敛代数统计

由图5可见，对于两车图片和三车图片，粒子群算法的收敛代数分布基本一致，主要集中在11～20代内收敛，图5的统计结果表明：对于不同类型的图片，算法的收敛性能是稳定的。

但是，K均值聚类算法需要预先指定聚类数目，实际应用中很难确定图片中车牌目标数，针对这一局限性，文中进行了如下测试：在两车图片中，将聚类数目指定为3，此时可以成功定位出2个车牌的正确位置，第3个子群的进化较为随机，一般收敛在图片中纹理变化较明显的非车牌区域，本文称之为误判区。在三车图片中，将聚类数目指定为2，可以成功定位出其中随机2个车牌的正确位置，会遗漏一个车牌目标区域。因此在实际应用中，可以适当放大聚类数目，以免遗漏；对于误判区，可通过后续的车牌字符识别进行剔除。

5 结 论

通过针对实际拍摄图片进行的仿真实验可见，结合K均值聚类和粒子群优化，可实现多目标优化。算法不需要对图片中目标的大致位置有先验经验，通过粒子群迭代可自动搜索定位到准确的多个目标区域，算法性能稳定、收敛，其定位的准确率能够满足实际的应用需求。

值得说明的是，K均值聚类方法需要人为设置所需的聚类个数，这在一定程度上限制了算法的应用范围。在下一步的研究中，可以考虑优化聚类算法，根据粒子特征自动设置、调整聚类个数，以提高算法的灵活性。

[1]范梅梅，廖东平.基于WLS-TIR的多目标识别认知雷达波形自适应方法[J].电子学报，2012（1）:73-77.

[2]秦洪峰.水下多目标定位关健技术研究[D].西安：西北工业大学，2002.

[3]高希报.图像中几种实用的目标定位方法研究与应用[D].南京：南京理工大学，2005.

[4]Y Qu，J Zhang.Cooperative localization based on the azimuth angles among multiple VAVs[C]//2013 International Conference on Unmanned Aircraft Systems（ICUAS），2013:818-823.

[5]曾雪，胡春华.帕金森病脑深部刺激疗法中STN靶点定位方法综述[J].北京:生命科学仪器，2014（3）:12-16.

[6]Ashtari A H，Nordin M J，Fathy M.An Iranian license plate recognition system based on color features[J].IEEE Transactions on Intelligent Transportation Systems，2014，15（4）：1690-1750.

[7]马永杰，云文霞.遗传算法研究进展[J].计算机应用研究，2012，29（4）:1201-1206.

[8]林俊，杨峰，林凯.Hough变换与先验知识在车牌定位中的新应用[J].计算机与数字工程，2009，37（8）:138-140.

[9]赵军伟.基于数学形态学和HSI颜色空间的人头检测[J].山东大学学报，2013（4）:6-10.

[10]周铁平，王庆.一种新的汽车牌照快速定位方法[J].网络新媒体技术，2007，28（4）:343-348.

[11]曾庆渝.视频分割算法研究及实践[D].杭州：浙江大学，2005.

[12]邢小红，罗军刚等.基于改进多目标粒子群算法的水库防洪调度[J].计算机工程与应用，2012，48（30）:33-39.

[13]冯琳，毛志忠等.一种改进的多目标粒子群优化算法及其应用[J].控制与决策，2012，27（9）:1313-1319.

[14]张岭军.基于多目标免疫算法的动态网络社区检测[D].西安：西安电子科技大，2012.

[15]Wickramasinghe U K，Li Xiaodong.Integrating User Preferences with Particle Swarms for Multiobjective Optimization[C]//Proc.Of the 10th Annual Conference on Genetic and Evolutionary Computation.Atlanta，USA:ACM Press，2008.

[16]陈东辉，刘志镜，王纵虎.一种基于粒子群优化的可能性C均值聚类改进方法[J].计算机科学，2012（11）:122-126.

[17]M.Baydoun，M.Dawi and H.Ghaziri，"Enhanced parallel implementation of the K-Means clustering algorithm，"2016 3rd International Conference on Advances in Computational Tools for Engineering Applications（ACTEA），Beirut，2016：7-11.

[18]李丹煜，杨庆山，田玉基.基于K-means聚类的风压系数快速分区方法[J].工程力学，2014（12）:164-172.