基于RGB三分量亮度法线相似度的立体匹配算法

高凯

（长春理工大学 电子信息工程学院，长春 130022）

稠密双目立体匹配是计算机视觉领域中广泛研究的问题之一。稠密立体匹配是三维重建、立体导航、非接触测距等技术的关键步骤，并且广泛应用于无人驾驶汽车（测距，导航）、机器人智能控制、遥感图像分析、安防监控、工业生产自动化、流水线控制等方面。立体匹配的目的就是找到在同一个场景中，两个摄像机采集到的图片之间的相应的匹配点，而这些相应点之间的位置差异就构成了视差图。一般来说，立体匹配算法包含四步[1］：匹配代价计算，代价聚合，视差计算和视差修正。第一，计算所有可能视差范围内的匹配代价；第二，计算每个像素支持区域内的代价聚合，而支持区域由局部匹配算法和全局匹配算法进行选择；第三，视差通过局部或者全局优化计算；第四，通过各种后处理方法进行视差结果修正。

根据能否得到基于区域的解，匹配算法可以分为全局算法和局部算法。一般来说，全局算法可以得到更精确的视差图。典型的全局算法是图割法[2］，置信度传播法[3，4］和动态规划法[5，6］，这些算法需要在能量函数中包含平滑因子。典型的局部算法是基于窗的代价聚合。基于自适应权值的局部立体匹配算法[7］提出了通过计算支持窗中像素值相似度和几何空间相似度来获得每个像素的权值。相比于全局方法，局部方法具有简单高效的特点，并获得了较好的视差结果。为了减少由Lab空间到RGB空间的信息损失，Geng等提出了RGB矢量空间中的立体匹配算法，其应用像素值相似度、空间几何距离相似度和梯度相似度来计算像素权值，获得了较精确的结果。受到Geng等的思想的启示，前期工作中提出了亮度法线的概念[9］，继而提出了基于亮度法线相似度、梯度相似度、像素值相似度和空间几何距离相似度的立体匹配方法，因为亮度法线反映了图像的高频信息，因此算法改进了视差图的边缘精度。本文在前期研究的基础上，分析了RGB三分量的特性，并提出了基于RGB三分量亮度法线矢量的局部立体匹配算法来改进视差图的精度。算法从RGB三分量亮度法线矢量反映的各分量的高频信息入手，分析其影响了立体匹配环节中的图片边缘的匹配精度，经与文献[8］比较，实验结果显示，本文提出的算法提高了图像边缘位置的匹配精度。

1 RGB三分量亮度法线的概念

在前期工作中[9］，提出了二维灰度图像的亮度法线矢量的概念。而对于RGB彩色空间的彩色图像，可以视为三个灰度图像的叠加，每一个分量都有一个亮度法线矢量，因此，提出了RGB三分量亮度法线矢量的概念。如图1所示，点A是含有RGB彩色分量的当前点，R平面代表R分量，G平面代表G分量，B平面代表B分量。

图1 计算RGB三分量亮度法线矢量示意图

例如，A可以表示为A（AR，AG，AB），其中AR，AG和AB分别为RGB空间中A点的红、绿、蓝彩色分量。B（BR，BG，BB）和C（CR，CG，CB）分别是计算A点法线矢量的临近点。A点到C点和A点到B点的矢量分别为：

A点的R，G和B分量的法线矢量通过矢量vec1i和vec2i的叉乘获得：

归一化A点的R，G和B分量亮度法线矢量：

其中，i∈{R，G，B}。

图2 RGB三分量法线相关结果

图2显示了彩色图像对的红绿蓝三分量的法线图像相关结果。图2（a）（b）分别是立体彩色图像的左右图像。图2（c）（d）（e）的第一行分别是左图像对应的红绿蓝成分，图2（f）（g）（h）的第一行分别是右图像对应的红绿蓝成分。图2（c）的第二行是红色分量的法线图像，图2（c）的最底一行是法线图像的模图像。其他图像依次类推。

根据图2显示，相同图像的RGB分量的灰度值是不同的，但立体图像对之间的R（BC）平面的灰度值确是相近的。图 2（c）（d）（e）（f）（g）（h）的第二行图像显示了法线矢量图像，其反映了第一行图像的高频信息，而高频信息对于立体匹配算法是有重要意义的，因此本文将RGB分量的法线矢量应用于立体匹配算法当中。

2 算法模型

本文提出通过计算彩色图像像素值相似度、空间几何距离相似度、梯度相似度和RGB亮度法线相似度的多相似度测量方法来计算支持窗权值。

2.1 支持权值计算

支持窗内像素的权值计算通过如下公式：

2.2 聚合与视差计算

参考图像与目标图像之间的窗内像素的权值计算用差异点函数E表示：

其中，Δcq→q→d，Δ gradxq→q→d，Δ gradyq→q→d和 Δnq，qd分别通过（9）（10）（11）（12）获得，λc，λgradx，λgrady，λn是常数。

其中D={dmin，…，dmax}是视差搜索范围。

2.3 视差修正

将左右两幅原图像分别作为目标图像和参考图像，进行两次匹配运算。会存在遮挡问题，因此为了修正视差，对两幅视差图进行一致性检测：

其中，dL(x，y)和dR(x，y)分别是左图像和右图像作为参考图像得出的视差。在一致性检测当中，如果失败，则视为是坏点，则用重新计算后的最大支持权重的像素的视差作为坏点位置的新视差。图3显示了修正后的视差结果。图3（e）是修正后的结果优于图3（b）初始结果.

图3 视差图修正

图4 实验比较结果

3 实验结果及讨论

立体图像对‘tsukuba’，‘venus’，‘teddy’，‘cones’由Middlebury测试平台提供。支持窗尺寸为35×35，常数τc=30，λc=40，τd=10，λgradx=20，λgrady=10 ，τg=30[8］，τn=40 ，λn=1对于测试图像对都是一致的。为了评价提出的算法，采用了Ground truth[1］和文献[7］中结果进行比较，图4为主观比较结果。图4（a）和图4（b）分别是彩色图像和ground truth。图4（c）和图4（d）分别是文献[8］和本文提出的视差图。本文实验中的误差门限Th=1.灰色和黑色区域越少，视差图精度越高，从图4（c）和图4（d）可以看出，本文提出的方法得到的结果优于文献[8］。特别强调的是，本文结果的边缘位置匹配精度明显提高。

为了获得客观的评价，Middlebury测试平台给出了相应的结果，视差图可以分为三个部分：所有像素，非遮挡区域，和深度不连续区。当生成的视差图和Groundtruth之间的绝对差小于Th，生成的视差图被认为是正确的。表1和表2分别是Th=1和Th=0.5对应的结果。为了评价提出算法的客观性，将提出的算法与其他局部自适应权值方法[7，8，10，11-13］进行比较。比较结果如表1和表2所示。提出的算法（ASW-N）提高了匹配精度，结果显示提出的算法得到的误匹配点低于其他方法，尤其是Th=0.5时，更为明显。提高的精度归功于RGB法线矢量相似度，也验证了其高频信息影响立体图像对的匹配精度的猜想。

4 结论

本文中，提出了基于彩色像素值相似度、空间距离相似度、梯度相似度和RGB三分量亮度法线矢量相似度的改进型自适应权值算法，通过对RGB三分量法线的分析，凸显了法线信息反映了图像的高频信息分量。通过增加法线信息来改进自适应权值计算方法。实验结果显示，相比于其他自适应权值算法，本文提出的算法可以提高匹配精度，尤其在含有纹理区域更为明显。从总体上来看，平均提高误匹配率达到0.4%。在今后的研究当中，会进一步根据图像的特点，研究相应的光学特性来改进算法。

表1 提出方法在Middlebury stereo benchmark中的特性比较（误差门限为1.0）

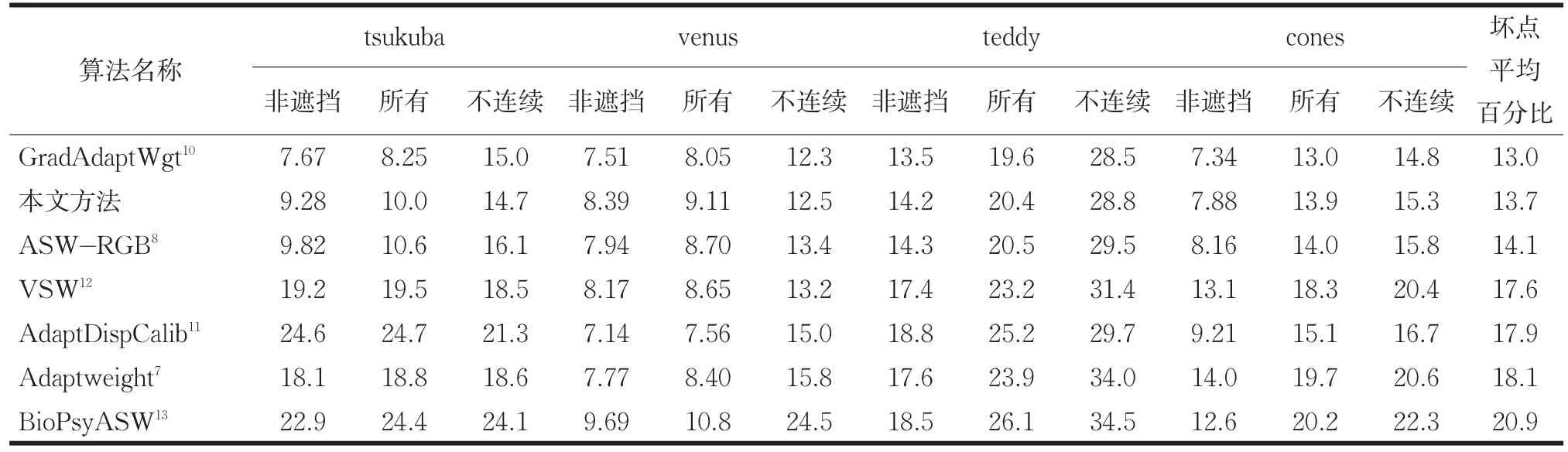
表2 提出方法在Middlebury stereo benchmark中的特性比较（误差门限为0.5）

[1]Scharstein D，Szeliski R.A taxonomy and evaluation of dense two-frame stereo correspondence algorithms[J］.InternationalJournal of ComputerVision，2002.47（1-3）：7-42.

[2]Hong L，Chen G.Segment-based stereo matching using graph cuts[C］.in Proceedings of IEEE Conference on Computer Vision and Pattern Recognition.2004.1（1）：74-78.

[3]Yang Q，Wang L，Ahuja N.A constant-space belief propagation algorithm forstereo matching[C］.in Proceedings of IEEE Conference Computer Vision and Pattern Recognition，2010：1458-1465.

[4]Sun J，Zheng N.-N.，Shum H.-Y..Stereo matching using beliefpropagation[J］.IEEE Trans.Pattern Anal.Machine Intell，2003，25（7）：787-800.

[5]Lei C，Selzer J，Yang Y.Region-tree based stereo using dynamic programming optimization[J］.ComputerVision and Pattern Recognition，2006（2）：2378-2385.

[6]Chang X，Zhou Z，Wang L，et al.Real-time accurate stereo matching using modified two-pass aggregation and winner-take-all guided dynamic programming[C］.International Conference on 3D Imaging，Modeling，Processing，Visualization and Transmission，2011：73-79.

[7]Yoon K.-J.，Kweon I.-S..Adaptive support-weight approach for correspondence search[J］.IEEE Trans.Pattern Anal.Mach.Intell，2006，28（4）：650-656.

[8]Yingnan Geng，Yan Zhao，Hexin Chen.Stereo matching based on adaptive support-weightapproach in RGB vectorspace[J］.Applied Optics，2012，51（16）：3538-3545.

[9]Kai Gao，Yan Zhao，He-xin Chen，et al.Stereo matching algorithm based on illumination normal similarity and adaptive support-weight[J］.Optical Engineering，2013.52（2）：027201-1--027201-7.

[10]De-MaeztuL，VillanuevaA，CabezaR.Stereo matching using gradient similarity and locally adaptive support-weight[J］.Pattern Recognition Letters，2011，32（13）：1643-1651.

[11]Gu Z，Su X，Liu Y，et al.Local stereo matching with adaptive support-weight，rank transform and disparity calibration[J］.Pattern Recogn.Lett，2008，29（9）：1230-1235.

[12]Hu W，Zhang K，Sun L，et al.Virtual support window for adaptive-weight stereo matching[J］.Visual Communications and Image Processing，2011（8）：1-4.

[13]L.Nalpantidis，A.Gasteratos.Biologically and psychophysically inspired adaptive support weights algorithm for stereo correspondence[J］.Robot.Auton.Syst，2010（58）：457-464.