光场强度分布对鬼成像成像质量的影响

王志峰，姚治海，高超，王晓茜

（长春理工大学 理学院，长春 130022）

鬼成像，又称为关联成像，是近些年兴起的新型成像技术[1-4］。传统的鬼成像系统中，光束被分束器分为相同性质的两束光，一束光通过待测物体后，被一个桶探测器接收，另外一路直接由一个具有空间分辨能力的探测器探测，对获得的光强信息进行关联计算，就可以恢复出物体的空间信息。鬼成像实验最早是利用自发参量下转换产生的纠缠光子实现的[5］，不久，人们发现使用热光源同样可以实现鬼成像[6-10］。相比于纠缠光，热光更容易获得，为鬼成像在实际应用奠定基础。因此，鬼成像的成像机理[11］及改善鬼成像的方案也就成了研究的热点问题[12-15］。

2008年，美国研究人员Shapiro提出了计算鬼成像方案[16］。相比传统鬼成像，计算鬼成像只需一条探测光路，即可恢复图像。计算鬼成像利用空间光调制器产生已知的光场，照射到物体上，并用桶探测器记录，桶探测器记录的总强度信号与已知的光场进行关联计算就可以恢复物体信息。罗春伶等人[17］利用空间光调制器，通过双曲余弦函数对高斯光源进行调制，改善了鬼成像的成像质量。吴令安等人[18］从理论上分析了光场的强度涨落对鬼成像成像质量的影响，通过数值模拟和理论计算发现光场的强度涨落影响了成像的对比度，当光场强度涨落更为剧烈时，对比度会有很大的提高。

本文中，把光场的强度分布分成两个部分来讨论，分别是光场的空间结构分布与一阶统计分布。光场的空间结构分布表现为散斑图中各个位置上的强度随空间坐标的变化情况，而光场的一阶统计分布则是考虑空间中一点散斑强度的统计特性[19-22］。并通过模拟与实验，验证了相比于光场的空间结构分布，其一阶统计性质对成像质量的影响更为明显。

1 理论模型

计算鬼成像实验系统如图1所示，计算机生成散斑图照射在物体上，通过探测器采集，并记录到计算机中，作为物臂的光场信息。同时，这些散斑图也可以作为参考臂的光场信息直接被存储到计算机中。对物臂和参考臂的光场信息进行二阶关联函数计算，从而恢复出物体的图像。

图1 计算鬼成像实验结构示意图

二阶关联函数可以表示为：

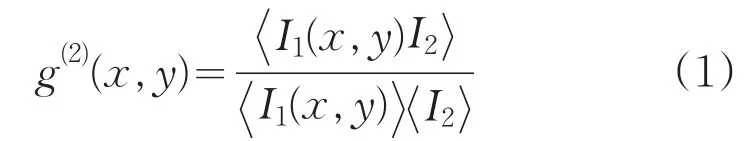
其中，I1(x，y)、I2分别代表两路的光场强度，...表示求系综平均。为了更好地研究光场的强度分布与二阶关联函数的关系，对二阶关联函数进行变换。

鬼成像的归一化二阶关联函数可以表示如下：

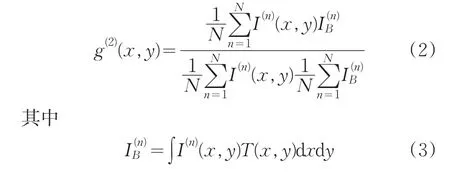
为了更客观地衡量光源强度分布对鬼成像成像质量的影响，引入对比度和衬噪比来评价所恢复图像的质量，其定义分别为[12，13］：

其中，Go和Gb分别为待测物体透光区和背景区关联函数值的系综平均，分别为对应位置关联函数值的方差。

2 数值模拟

通过数值模拟来验证光场强度分布的不同与鬼成像成像质量的关系。为了便于分析，将光场的空间结构分布与统计分布分别调制成高斯分布与均匀分布。用gg表示空间结构分布和一阶统计分布均为高斯分布的散斑图，用gu表示空间结构的分布为高斯分布，一阶统计分布为均匀分布的散斑图，用ug表示空间结构的分布是均匀分布，一阶统计分布是高斯分布的散斑图，用uu表示空间结构的分布和一阶统计分布均为均匀分布的散斑图。

如图所示，从图2（a）～（d）这4张散斑图可以明显的看出，当空间结构的分布为高斯分布时，散斑图的中心区域较亮且周围较暗，空间结构的分布为均匀分布时，整个散斑图的亮暗是相对均匀的。

为了区分其统计性质的差异，分别对四种散斑图进行了30000次的采样，从而得到了四种散斑图中某一点随时间变化的一阶统计分布，如图2（e）～（h）所示，分别对应了不同空间分布下的一阶统计性质，两组数据相结合，验证了实验中所使用的散斑图符合预期。

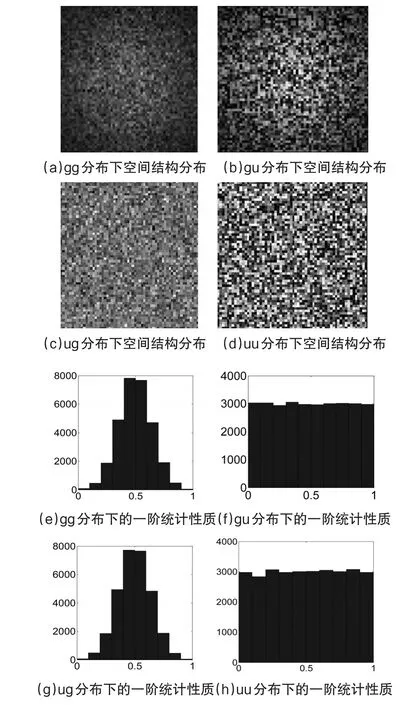
图2 不同强度分布下的空间结构分布（a～d）及其一阶统计性质（e～h）

图3为不同强度分布的光源下30000次采样的数值模拟结果，图3（a）为模拟时所使用的物像。图3（b）为空间分布和统计分布都是高斯分布的光场，图3（c）统计分布为均匀分布，空间分布为高斯分布的光场，图3（d）统计分布为高斯分布，空间分布为均匀分布的光场，图3（e）空间分布和统计分布皆为均匀分布的光场。从图3可以得出，在相同采样次数的情况下，光源空间分布与统计分布的不同，会对鬼成像的成像质量产生明显的影响。

通过图3（b）～（e）这四幅图的对比，可以发现，当只改变光源的一阶统计分布时，鬼成像的成像质量有了显著的提高，当只改变光源的空间分布时，其成像质量的变化并不是很明显。为了更好地评估成像质量，利用（4）、（5）式来计算不同强度分布下，对比度和衬噪比随采样次数的关系变化曲线，如图所示：

图3 物像图（a）和光场强度分布不同的情况下鬼成像模拟结果图（b～e）

如图4和图5所示，n为模拟时的采样次数，n=1000开始统计，从图4、图5可以得出，所恢复图像的对比度和衬噪比会随着采样次数的增加而增大。在相同的采样次数下，当光源的一阶统计分布由高斯分布变为均匀分布时，图像的对比度和衬噪比有了非常显著的提高。当只改变光源的空间结构分布，将空间分布为高斯分布的光源变为均匀分布时，成像质量也有细微的差别，但影响并不是很大。

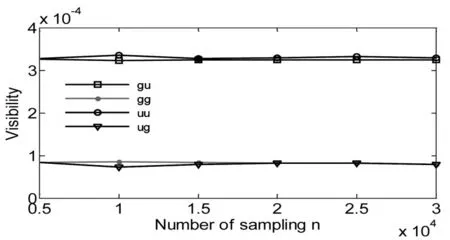
图4 不同强度分布与采样次数下对比度的变化曲线

图5 不同强度分布与采样次数下CNR的变化曲线

综上数值模拟的结果，发现光源强度分布的不同会对鬼成像的成像质量产生影响。其中，光源的一阶统计分布的改变对成像质量的影响尤为明显，而空间结构的分布的变化则会产生较小的作用。

3 实验验证

实验中所使用的实验系统是以计算鬼成像为基本架构搭建的，与传统计算鬼成像不同的是，光源为投影仪光源而非激光光源。利用计算机生成光场分布不同的随机散斑，将散斑图以投影仪光源为载体，照射在待测透射物体上。

图6 不同强度分布下鬼成像实验结果图

图6（a）～（d）为采样次数是20000次的情况下，不同强度分布的光源的成像图。图6（a）的一阶统计分布和空间结构的分布皆为高斯分布；图6（b）的一阶统计分布为高斯分布，空间结构的分布为均匀分布；图6（c）的一阶统计分布为均匀分布，空间结构的分布为高斯分布；图6（d）的一阶统计分布和空间结构的分布皆为均匀分布。

由上述成像的结果表明，当改变光场的一阶统计分布时，鬼成像的成像质量有了显著的提高。而仅仅改变光场空间结构的分布对成像质量的影响则不是那么的明显。为了更客观地评价成像质量的变化，通过计算恢复图像后的对比度和衬噪比来进行比较。

图7和图8分别描述了强度分布不同的光源，其对比度和衬噪比随采样次数增加的变化趋势。如图可知，当光源的一阶统计分布为均匀分布时，成像质量相比于高斯分布有了明显的提高，而空间结构的分布的不同对成像质量的影响相对比较微弱。

图7 不同强度分布与采样次数下对比度的变化曲线

图8 不同强度分布与采样次数下CNR的变化曲线

4 结论

本文从光场的强度分布入手，分别考虑了光场的空间结构分布与一阶统计分布，利用计算机生成空间结构分布与一阶统计分布不同的散斑来模拟不同强度分布的光场，通过数值模拟和实验结果表明：相比于光场的空间结构分布，其一阶统计性质会对成像质量产生较大的影响。为了更客观地评价成像质量的变化，引入了对比度和衬噪比这两个衡量图像质量的指标，验证了在相同的采样次数下，改变光场的一阶统计性质会对图像的对比度和衬噪比会产生更大的影响，并发现了当光场的一阶统计分布为均匀分布时，其成像质量有了显著的提高，因此可以只通过调节光场的一阶统计分布而提高鬼成像的成像质量。

[1]Bennink RS，Bentley SJ，Boyd RW."Two-Photon"coincidence imaging with a classicalsource[J］.Phys Rev Lett，2002，89（11）：113601-1-113601-3.

[2]Gatti A，Brambilla E，Bache M，et al.Ghost imaging with thermal light：comparing entanglement and classical correlation[J］.Phys Rev Lett，2004，93（9）：093602-1-093602-4.

[3]Wang K，Cao D Z.Subwavelength coincidence interference with classicalthermallight[J］.Phys Rev Lett，2004，70（4）：628-628.

[4]Zhang D，Zhai YH，Wu LA，et al.Correlated twophoton imaging with true thermallight[J］.Opt Lett，2005，30（18）：2354-2356.

[5]Pittman T B，Shih Y H，Strekalov D V，et al.Optical imaging by means of two-photon quantum entanglement[J］.Phys Rev A，1995，52（5）：R3429-R3432.

[6]Ferri F，Magatti D，Gatti A，et al.High-resolution ghost image and ghost diffraction experiments with thermallight[J］.PhysRevLett，2005，94（18）：183602-1-183602-4.

[7]Meyers R，Deacon KS，Shih Y.Ghost-imaging experiment by measuring reflected photons[J］.Phys Rev A，2008，77（4）：1912-1917.

[8]Liu Q，Chen X H，Luo K H，et al.Role of multiphoton bunching in high-order ghost imaging with thermal light sources[J］.Phys Rev A，2009，79（5）：1744-1747.

[9]Chen X H，Agafonov I N，Luo K H，et al.Highvisibility，high-orderlensless ghostimaging with thermal light[J］.Opt Lett，2010，35（8）：1166-1168.

[10]KandjaniS A，KheradmandR，DadashzadehN.Ghostimaging with pseudo-thermallight[C］.TransparentOpticalNetworks（ICTON），2011 13th International Conference on.IEEE，2011：1-4.

[11]Gao C，Wang X，Wang Z，et al.Optimization of computationalghostimaging[J］.PhysRev A，2017，96（2）.

[12]刘雪峰，姚旭日，李明飞，等.强度涨落在热光鬼成像中的作用[J］.物理学报，2013，62（18）：184205-1-184205-7.

[13]Chan K W C，O'Sullivan M N，Boyd R W.Optimization of thermal ghost imaging：high-order correlations vs.background subtraction[J］.Optics Express，2010，18（6）：5562-5573.

[14]于佳意，常锋，姚治海，等.三阶鬼成像的可见度研究[J］.长春理工大学学报：自然科学版，2016，39（3）：124-127.

[15]董博，姚治海，李喆，等.压缩感知OMP算法与IRLS算法在计算鬼成像中的对比分析[J］.长春理工大学学报：自然科学版，2016（1）：21-27.

[16]Shapiro J H.Computational ghost imaging[J］.Phys.Rev.A，2008，78（6）：061802-1-061802-2.

[17]Luo C L，Xu H，Cheng J.High-resolution ghost imaging experiments with cosh-Gaussian modulated incoherent sources[J］.J Opt Soc Am A，2015，32（3）：482-485.

[18］Arecchi F T.Measurement of the statistical distribution of Gaussian and laser sources[J］.Physical Review Letters，1965，15（24）：912-916.

[19]Zhang M H，Wei Q，Shen X.et al.Statistical opticsbased numericalmodeling ofghostimaging and its experimental approval[J］.Acta Optica Sinica，2007，27（10）：1858-1866.

[20]姚银萍，万仁刚，薛玉郎，等.基于统计光学的正负热光非定域成像[J］.物理学报，2013，62（15）：162-169.

[21]Bo Z W，Gong W L，Yan Y.et al.Experimental research of ghost imaging based on photon counting[J］.Chinese Journal of Lasers，2016，43（11）：3510-3515

[22]Goodman J W.Speckle phenomena in optics：theory and applications[M］.America：Roberts&company，2007.