初窥考点 直击中考

李兆龙 范大阳

生活中，数据是一种重要的信息资源，收集、整理、描述数据是数据处理的一个基本过程.下面就让我们初窥中考真题，探究解题切入点，获得解题技法，以便举一反三.

考点一 概念的考查

1.调查方式的采用.

例1 （2017·贵州黔南）下列调查中，适宜采用全面调查（普查）方式的是（ ）.

A.了解我国民众对乐天集团“萨德事件”的看法

B.了解湖南卫视《人民的名义》反腐剧的收视率

C.调查我校某班学生喜欢上数学课的情况

D.调查某类烟花爆竹燃放的安全情况

【解析】A、B选项进行全面调查，工作量太大，D选项存在破坏性，都不适合全面调查，故选C.

【方法小结】当调查的对象不需要花费太多的时间，而且不具有破坏性时，可采用普查.有些情况下，必须采用普查，如对载人飞船的零部件的检查，因为对安全要求高，在科学知识等方面不能出现任何差错.当问题中个体数较多，普查的工作量大，或受客观条件的限制，不适合用普查时，可采用抽样调查的方法.

2.总体、个体、样本、样本容量.

例2 （2015·山东聊城）电视剧《铁血将军》在我市拍摄，该剧展示了抗日英雄范筑先的光辉形象.某校为了了解学生对“民族英雄范筑先”的知晓情况，从全校2400名学生中随机抽取了100名学生进行调查.在这次调查中，样本是（ ）.

A.2400名学生

B.100名学生

C.所抽取的100名学生对“民族英雄范筑先”的知晓情况

D.每一名学生对“民族英雄范筑先”的知晓情况

【解析】首先判断出这次调查的总体是什么，然后根据样本的含义——从总体中取出的一部分个体叫作这个总体的一个样本，可得在这次调查中，样本是所抽取的100名学生对“民族英雄范筑先”的知晓情况，据此解答即可.答案选C.

【方法小结】此题主要考查了总体、个体、样本、样本容量的含义和应用，要熟练掌握.解答此题的关键是要明确总体、个体、样本、样本容量等的概念.

3.频数和频率.

例3 （2016·贵州毕节）为了提高学生书写汉字的能力，增强保护汉字的意识，某校举办了首届“汉字听写大赛”，学生经选拔后进入决赛，测试同时听写100个汉字，每正确听写出一个汉字得1分.本次决赛，学生成绩为x（分），且50≤x＜100，将其按分数段分为五组，绘制出以下不完整表格：

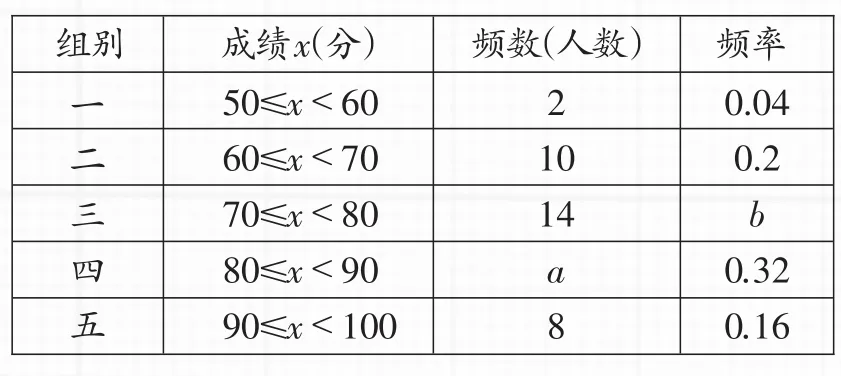
组别2 0.04 0.2 b 0.32 0.16一二三四五成绩x（分） 频数（人数） 频率50≤x＜60 60≤x＜70 70≤x＜80 80≤x＜90 90≤x＜100 10 14 a 8

请根据表格提供的信息，解答以下问题：

（1）本次决赛共有____名学生参加；

（2）直接写出表中a=_____，b=______.

【解析】（1）频率等于频数除以总数，除了第三组和第四组外，其他任意一组的频数除以频率后均可得到参加学生的总数为50；（2）总数求出来后，就可以求出a为16，b为0.28.

考点二 样本的代表性和广泛性

例4 （2017·四川内江）为了解某市老人的身体健康状况，需要抽取部分老人进行调查，下列抽取老人的方法最合适的是（ ）.

A.随机抽取100位女性老人B.随机抽取100位男性老人C.随机抽取公园内100位老人D.在城市和乡镇各选10个点，每个点任选5位老人

【解析】为了解某市老人的身体健康状况，A、B、C样本不具有代表性，故选D.

例5（2015·浙江嘉兴）质检部门为了检测某品牌电器的质量，从同一批次共10000件产品中随机抽取100件进行检测，检测出次品5件.由此估计这一批次产品中的次品件数是（ ）.

A.5 B.100 C.500 D.10000

【解析】先求出次品所占的百分比，再根据生产这种零件的数量10000件，直接相乘得出答案即可.答案选C.

【方法小结】在样本合理的前提下，某一项目（比如本题中的次品）在样本中所占的比值可以认为与在总体中所占的比值是相等的，从而用这样的比值去估计总体.

考点三 统计图表

例6 （2017·北京）下面的统计图反映了我国与“一带一路”沿线部分地区的贸易情况.2011-2016年我国与东南亚地区和东欧地区的贸易额统计图如下.

（以上数据摘自《“一带一路”贸易合作大数据报告（2017）》）根据统计图提供的信息，下列推理不合理的是（ ）.

A.与2015年相比，2016年我国与东欧地区的贸易额有所增长

B.2011-2016年，我国与东南亚地区的贸易额逐年增长

C.2011-2016年，我国与东南亚地区的贸易额的平均值超过4200亿美元

D.2016年我国与东南亚地区的贸易额比我国与东欧地区的贸易额的3倍还多

【解析】由折线统计图可得2011-2014年我国与东南亚地区的贸易额逐年增长，2015年有所下降，故此选项错误，故选B.

例7 （2017·江西）为了解某市市民“绿色出行”方式的情况，某校数学兴趣小组以问卷调查的形式，随机调查了某市部分出行市民的主要出行方式（参与问卷调查的市民都只从以下五个种类中选择一类），并将调查结果绘制成如下不完整的统计图.

种类出行方式A C E共享单车B 步行公交车D 的士私家车

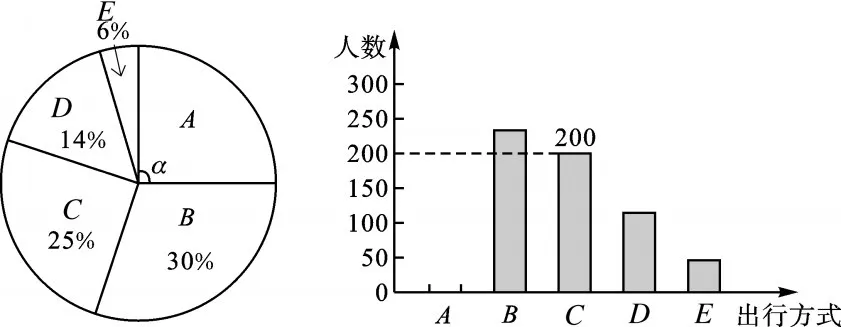
根据以上信息，回答下列问题：

（1）参与本次问卷调查的市民共有____人，其中选择B类的人数有______人；

（2）在扇形统计图中，求A类对应扇形圆心角α的度数，并补全条形统计图；

（3）该市约有12万人出行，若将A、B、C这三类出行方式均视为“绿色出行”方式，请估计该市“绿色出行”方式的人数.

【解析】（1）200÷25%=800（人），所以参与本次问卷调查的共有800人，其中选择B类的共有800×30%=240人.（2）A类人数所占百分比为1-（30%+25%+6%+14%）=25%，A类对应扇形圆心角α的度数为360×25%=90°，A类人数为800×25%=200，补全条形统计图见下图.（3）12×（25%+30%+25%）=9.6（万）.

例8 （2016·河南）在一次社会调查活动中，小华收集到某“健步走运动”团队中20名成员一天行走的步数，记录如下：

5640 6430 6520 6798 7325 8430 8215 7453 7446 6754 7638 6834 7326 6830 8648 8753 9450 9865 7290 7850

对这20个数据按组距1000进行分组，并统计整理，绘制了如下尚不完整的统计图表：

请根据以上信息解答下列问题：

（1）填空：m=_____，n=______；

（2）补全频数统计图；

（3）若该团队共有120人，请估计其中一天行走步数不少于7500步的人数.

【解析】（1）根据题目中所给的数据，确定在7500≤x＜8500这个范围内数据的个数即可，得m的值为4，由在9500≤x＜10500这个范围内数据的个数得n的值为1.

（2）根据（1）所得的数据补全统计图如下：

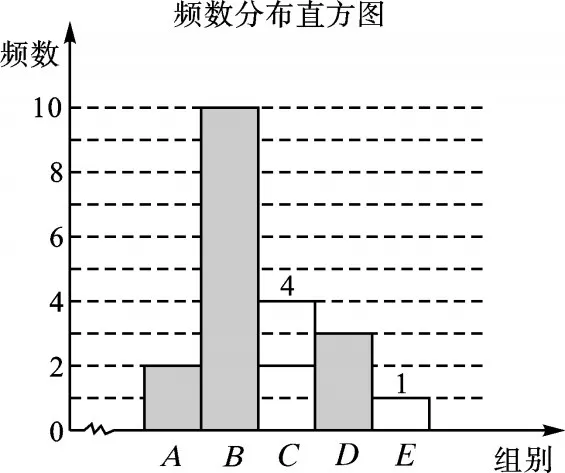
（3）用该团队的总人数乘一天行走步数不少于7500步的人数所占的比重即可得答案为48人.

解决关于数据的题目时，要能正确读懂题意，理解相关概念，能通过数据的收集、描述、分析做出合理决策.希望同学们通过典型题目进行训练，能够真正适应中考题.