利用多岛遗传算法的侧式进/出水口体型优化研究
高学平,李建国,孙博闻,田 野,张 翰
(天津大学 水利工程仿真与安全国家重点实验室,天津 300350)
1 研究背景
抽水蓄能电站进/出水口具有双向水流的特点,其体型设计应同时考虑进流和出流两种工况下的水力特性要求,包括出流时水流均匀扩散、拦污栅断面避免反向流速,以及进/出流时应尽可能减少水头损失等[1]。
针对抽水蓄能电站侧式进/出水口,国内学者通过物理模型试验和数值模拟方法,较全面地分析了进/出水口扩散段体型变化对孔口流速分布[2]、水头损失[3]、流量分配[4]等的影响,所得到的规律为进/出水口体型优化奠定了基础。例如,高学平等[5-6]指出侧式进/出水口扩散段对水头损失和孔口流态具有决定性作用,研究了扩散段体型参数对孔口间流量分配的影响。张兰丁[7]等通过调整扩散段体型分析了侧式进/出水口出流时流速分布不均匀与水头损失系数偏大的问题。蔡付林等[8]通过水工模型试验,指出扩散段分流墩布置形式对流速分布有一定的影响。杨小亭等[9]总结现有模型试验资料,指出扩散段顶板扩散角、流速分布、各孔口流量分配等均对水头损失产生重要影响。沙海飞等[10]通过数值模拟优化扩散段改善了进/出水口的流速不均匀系数偏大等现象。上述研究均是从水力特性的角度寻求较优的进/出水口体型,即通过物理模型试验或数值模拟对设定体型进行水力特性研究,针对不利的水力指标调整体型再进行研究,直至获得满意的体型。该类体型优化方法属于传统的研究方法,其缺点是对研究者的经验依赖性强,重复性操作多;对于数值模拟方法,建模效率低、CFD计算耗时长;对于模型试验方法,试验周期长、试验成本高。
实际上,大多数体型优化问题都可以看成多目标优化问题,而多目标优化问题存在多个最优解集,因此在工程中往往将其转化为各目标之加权和,然后采用单目标优化技术进行分析求解[11]。多岛遗传算法(multi-island genetic algorithm,MIGA)是一种典型的单目标优化算法,由于其寻优能力好、鲁棒性强等特点,在水下航行器[12]、机翼形建筑物[13]、管道[14]、无人机进气道[15]等多种研究对象得到广泛应用。上述体型优化研究均是在单向流动条件下进行的,而抽水蓄能电站侧式进/出水口为双向水流,需要综合考虑进流和出流两种工况下可能存在如水头损失系数过大、断面流速不均匀系数偏大及孔口间流量分配不均匀等水力学问题,因此双向水流条件下的体型优化问题更复杂。
围绕双向水流条件下的侧式进/出水口体型优化这一多目标优化问题,本文采用加权法将其转化为单目标优化问题,利用多岛遗传算法进行体型优化。优化时以加权后的进流和出流两种工况下的水头损失系数为目标函数,以孔口断面流速不均匀系数和孔口间流量不均匀系数为约束条件。鉴于扩散段体型对进/出水口水力特性有很大影响,本文将扩散段作为优化的重点,选择扩散段长度、孔口高度和分流墩尾墩中孔宽度等作为优化变量,对进/出水口体型进行水力优化研究。为提高建模速度与优化效率,采用参数化建模的方法和基于CFD的响应面模型进行优化计算。
2 模型建立与验证
2.1 参数化建模对于侧式进/出水口,沿进流方向依次为防涡梁段、调整段、扩散段和渐变段。由于扩散段体型对其水力特性有决定性影响,因此重点优化该段体型。侧式进/出水口体型及扩散段体型参数如图1所示,主要体型参数有:孔口高度HO,孔口宽度WO,扩散段长度LDS,扩散段末端高度HDS,宽度WDS,尾墩处中孔宽度WDSM,边孔宽度WDSS,水平扩散角θ和垂直扩散角α。在优化过程中,各体型参数满足的几何关系如下:
(1)进/出水口体型对称,各孔口尺寸一致:

(2)为保证拦污栅断面流速相当,单孔过流面积保持不变:

(3)分流墩尾墩处断面尺寸不变:

(4)扩散段水平扩散角θ,竖直扩散角α:
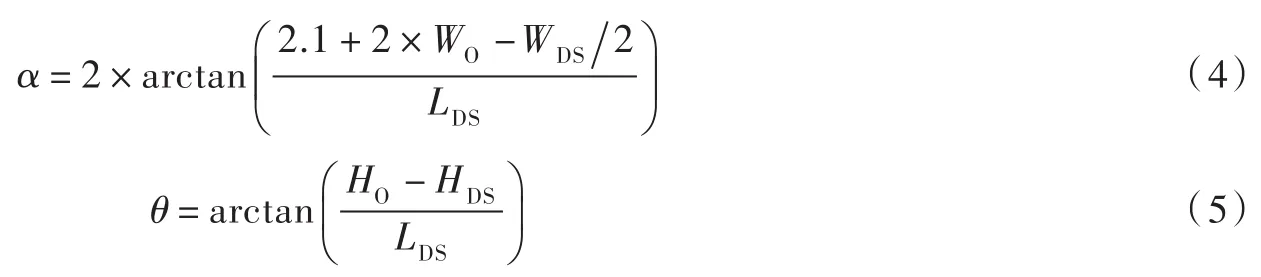
本文以某抽水蓄能电站下水库侧式进/出水口为例进行研究。以往对进/出水口数值模拟与体型优化研究大多依据工程经验调整扩散段体型,任一几何尺寸的调整都需要重新建立模型。为实现自动寻优的优化设计[16],因此本文采用UG®进行参数化建模。由于扩散段长度(LDS)、孔口高度(HDS)和分流墩尾墩中孔宽度(WDS)对进/出水口水力特性影响较大[3,7],因此本文选取这3个体型参数作为优化变量,给定其取值范围;进/出水口其他部位根据扩散段的变化做出相应调整。扩散段各体型参数取值范围列于表1。
计算区域如图2所示,包括部分下水库、尾水明渠、进/出水口和部分尾水隧洞。进流时,水体由库区流向隧洞;出流时,水体由隧洞段流向库区。库区边界,距进/出水口140 m的库区断面,给定水库水位;隧洞边界,距事故闸门井渐变段末端20倍洞径(20D)的隧洞断面,按流量给定流速;固壁边界采用无滑移条件。进/出水口体型采用六面体网格,孔口附近网格尺寸为0.3 m,其余部位0.3~1.0 m不等,不同体型参数下进/出水口总网格数110万~130万不等。
2.2 控制方程包括连续性方程和动量方程,并利用Realizablek-ε模型对其封闭。
(1)连续性方程
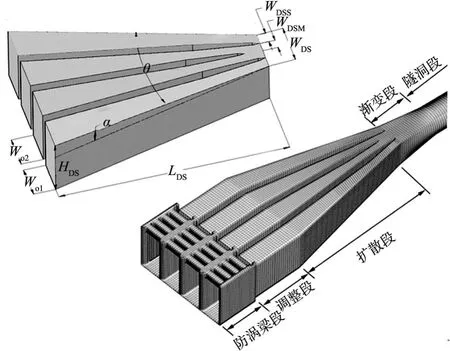
图1 侧式进/出水口体型及扩散段体型参数

表1 扩散段各体型参数取值范围
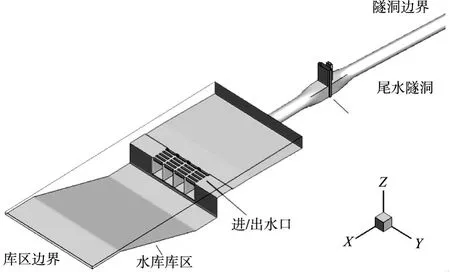
图2 计算区域

(2)动量方程
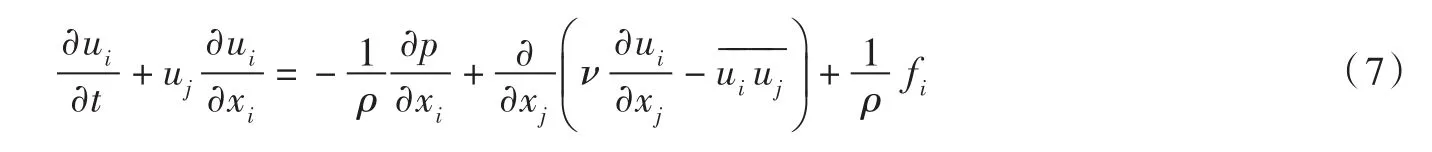
(3)k方程
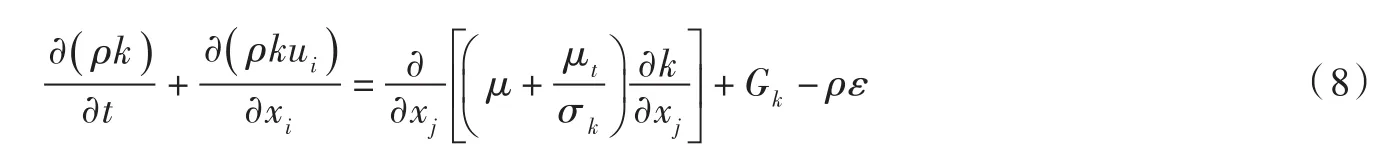
(4)ε方程
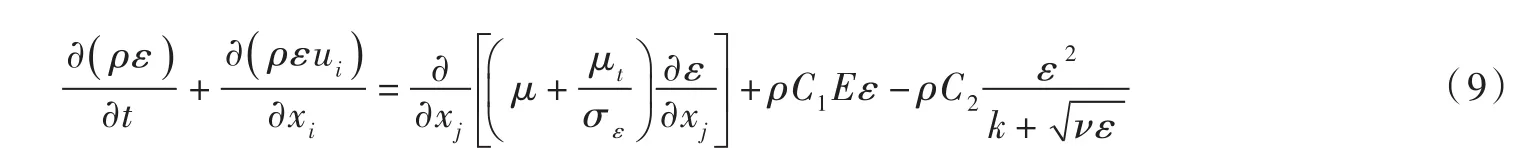
本文采用商业软件Fluent®进行计算,方程求解采用有限体积法,空间离散采用二阶迎风格式,压力—速度耦合采用SIMPLE算法。
2.3 模型验证利用建立的数学模型对该侧式进/出水口体型进行了数值模拟,研究进/出水口拦污栅断面流速分布和流量分配,并与该侧式进/出水口的模型试验结果进行了比较。进流和出流工况下拦污栅断面中边孔流速分布绘于图3,孔口间流量分配列于表2。图3流速分布的数值模拟和试验基本一致,但断面中部流速数值模拟值略大,数值模拟网格大小和试验测量精度均可能造成这种偏差。表2流量分配数值模拟与试验基本吻合。总体而言,数值模拟结果值与试验值吻合较好,该数学模型能够应用于体型优化研究。
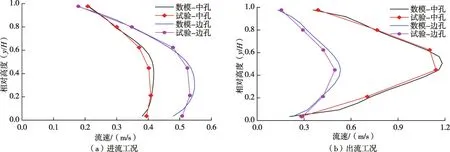
图3 拦污栅断面中边孔中垂线的流速分布
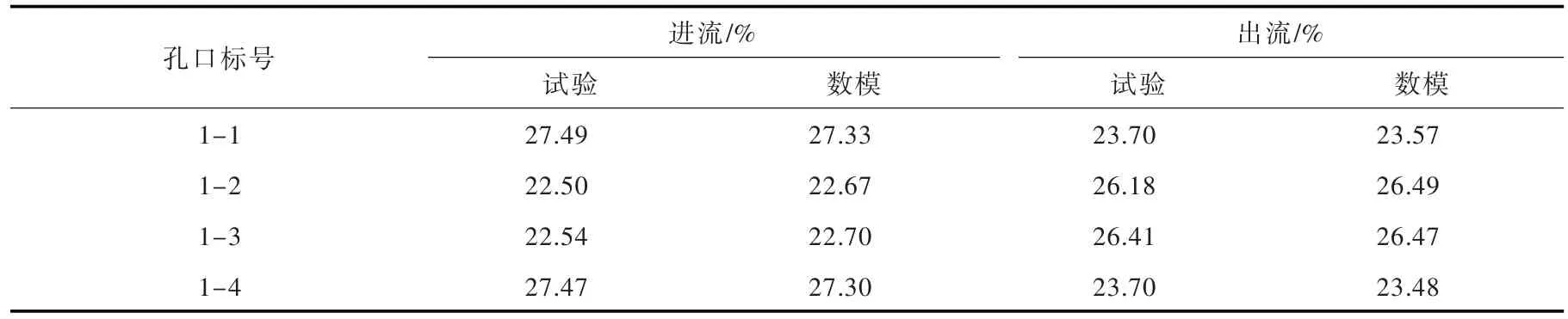
表2 孔口间流量分配
3 优化设计方法
首先,在原体型的基础上,对孔口高度、扩散段长度和分流墩尾墩处中孔宽度等优化变量进行调整,得到一系列不同的式进/出水口体型,形成侧式进/出水口体型样本空间。然后从样本空间选取侧式进/出水口体型样本点,并采用Fluent软件进行流场计算,得到进/出流条件下水头损失系数、流速不均匀系数和流量不均匀系数等水力指标。为减少后续寻优计算时对CFD计算程序的调用,提高优化计算的有效性,本文利用响应面模型,通过函数关系式描述水力指标值与优化变量的关系。针对侧式进/出水口体型优化这一多目标优化问题,本文通过水力指标进行体型寻优,将加权后水头损失系数作为优化的目标函数。同时,将以孔口流速不均匀系数和孔口间流量不均匀系数作为约束条件。多岛遗传算法是一种全局优化算法,优化效率高,本文采用该优化算法进行体型优化。
3.1 响应面模型优化变量任意组合才能保证得到侧式进/出水口最佳体型,即优化过程需要覆盖优化变量调整而形成的整个样本空间。为达到这一目标本文采用响应面模型[17],通过足够的样本点数据模拟出整个响应曲面,并利用函数关系式描述水力特性指标与优化变量的关系。改良的拉丁超立方实验设计方法[18]是一种多维分层抽样方法,具有速度快、样本空间覆盖均匀的特点,故将其用于本文侧式进/出水口的空间抽样。响应面模型的应用可以减少后续优化中对CFD计算程序的调用,极大地节约计算时间,提高优化效率。响应面模型的精度由相关系数R2进行评定[19],经计算本文所采用的响应面模型R2=0.97>0.9,可满足精度要求。
3.2 多岛遗传算法遗传算法是借鉴生物在自然状态下的遗传和进化过程而发展形成的一种全局优化算法[20]。多岛遗传算法是在传统遗传算法的基础上形成的一种基于群体分组的并行性遗传算法。不同于传统遗传算法,多岛遗传算法将初始种群划分为多个子群,并将各子群在不同的“岛屿”上互相隔离,使各个子群能够独立地进化,并非整个种群采用相同的进化方法,同时各个“岛屿”之间通过一定时间内的“迁移”操作进行信息交换。多岛遗传算法能够显著地提高运算速度,同时若干子群独立进化可以提高整个种群的遗传多样性,所以还可以避免传统遗传算法的早熟现象,进而寻找全局最优解[21]。表3为本文采用的多岛遗传算法参数设置。

表3 多岛遗传算法参数设置
3.3 目标函数及约束条件侧式进/出水口水头损失大小直接影响抽水蓄能电站运行效益。为获得最大经济效益,本文将进流和出流工况下水头损失系数作为目标函数进行优化计算,以期得到水头损失系数最小时的进/出水口设计体型。同时,选取孔口流速不均匀系数和孔口间流量不均匀系数作为约束条件,以满足设计对水力特性的要求。
3.3.1 目标函数 为综合考虑侧式进/出水口进流和出流两种工况下水头损失系数,为协调各目标获得整体优化体型,本文采用线性加权法对多目标函数进行处理[22],通过指定权重系数将多目标优化问题转化为单一目标优化问题[23],进而通过多岛遗传算法进行求解。
线性加权法的好处在于可以通过调整目标函数中权重系数ω1、ω2的值来体现进流或出流的重要性[24]。经计算发现,当进流和出流权重系数分别为0.33和0.67,即比值为1∶2时,综合水头损失系数(进流与出流工况水头损失系数之和)有最小值,此时得到体型可作为推荐体型。利用权重系数构建双向水流条件下水头损失目标函数F为:

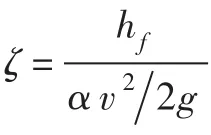
在遗传算法中,往往将目标函数进行变换得出适应度函数。在构造适应度函数时应尽量减小计算量,且各点适应度函数的值与解的优劣性成反比[25],本文适应度函数为:

式中b取目标函数中最小值。
3.3.2 约束条件 侧式进/出水口拦污栅处流速不均匀系数指过栅最大流速与过栅平均流速的比值。《抽水蓄能电站设计导则》[26]并未对流速不均匀系数做出明确要求,结合工程经验[4,9],一般要求出流工况该值小于2,因此本文设定出流工况流速不均匀系数上界为1.8。
流量不均匀系数指相邻孔口流量相差的百分比,规范推荐小于10%,但研究表明该推荐值难于满足,而小于20%更符合工程实际[3],因此本文设定进/出流工况下流量不均匀系数取值上界为20%。
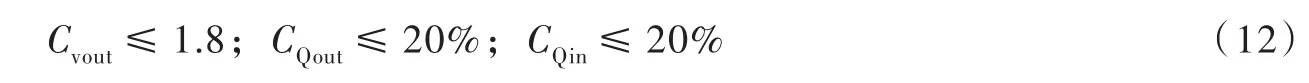
式中:Cvout为出流工况的孔口流速不均匀系数;CQout、CQin为进流和出流工况的流量不均匀系数。
4 优化结果分析
本文采用CFD对侧式进/出水口进行水力计算,得到进/出流条件下水头损失系数、流速不均匀系数和流量不均匀系数等水力指标,利用响应面模型得到水力指标和优化变量的函数关系。针对双向水流条件下侧式进/出水口体型优化的多目标问题,通过水力指标进行体型寻优,将加权后水头损失系数作为优化的目标函数。同时,将以孔口流速不均匀系数和孔口间流量不均匀系数作为约束条件。为获得水力指标最优的体型,采用多岛遗传算法作为优化算法进行全局优化。
4.1 优化结果分析图4为适应度随进化代数的变化过程。由图4看出,种群适应度在第5代急速增加,之后保持平稳增长,系统优良性一直在改善;在第35代时适应度值0.8973,接近于1,认为此时适应度函数有最优解[22]。图5为目标函数值与扩散段体型参数的关系,图中三维曲面代表目标函数值的分布,由图5看出目标函数值存在多个局部最优解,而多岛遗传算法能够避免早熟现象,从而利于获得全局最优解。
从计算效率而言,本次侧式进/出水口体型优化共进行100代总计10 000次迭代,同等的数量的CFD计算在常规的计算机配置下是难以实现的。本文所采用的参数化建模方法和基于CFD的响应面模型,加快了方案比选中的建模与数值模拟速度、提高了设计精度以及减少了研究者经验的依赖度,从而提高了全局优化效率。
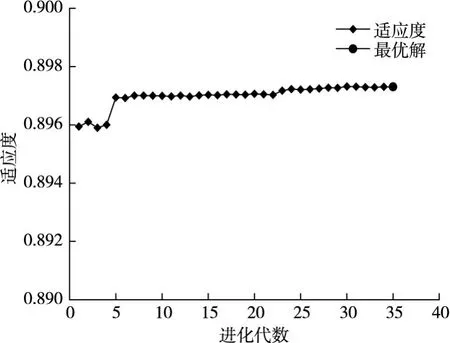
图4 适应度与进化代数的关系曲线
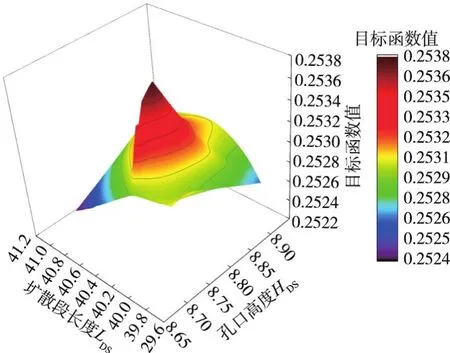
图5 目标函数值与扩散段体型参数关系
4.2 推荐体型水力特性图6为原体型与推荐体型的扩散段尺寸。相对于原体型,推荐体型的孔口高度由9.80 m降低为8.91 m,为保证过流面积不变,相应的孔口宽度由5.60 m增加到6.17 m;扩散段长度由36.00 m延长至40.89 m;分流墩尾墩处中孔宽度由1.58 m减小到1.51 m,边孔宽度由2.02 m增至2.09 m。
表4为推荐体型与原体型的各项水力指标的对比。推荐体型的各项水力指标较原体型有明显改善,水头损失系数ζ,出流工况的ζ降低7.51%;进/出流总水头损失系数(进流与出流水头损失系数之和)降低3.35%。流速不均匀系数Cv,进流工况的Cv两种体型相差不大且均较优,但出流工况的Cv得到明显改善,减小了14.50%(推荐体型1.799,原体型2.104)。孔口间流量不均匀系数CQ,原体型出流工况的流量较为均衡,但进流工况的孔口间流量分配极不均匀(大于20%);推荐体型出流工况有所变差,但进流工况的孔口间流量分配趋于均匀,且进/出流时差别较小(1%),双向水流条件下得到整体优化,且CQ均小于20%。
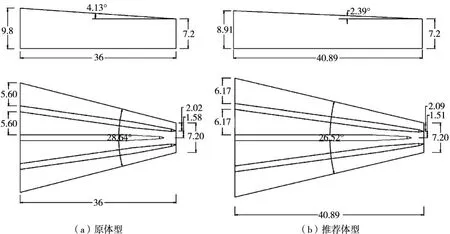
图6 原体型与推荐体型的扩散段尺寸(单位:m)

表4 原体型与推荐体型进/出水口的水力特性
图7为出流工况原体型与推荐体型的中边孔拦污栅断面的中垂线的流速分布。图8为进/出水口4孔口拦污栅断面流速云图。由图看出,原体型中孔顶部存在明显的反向流速区,且流速不均匀系数偏大;推荐体型在拦污栅处没有反向流速,流态得到改善。
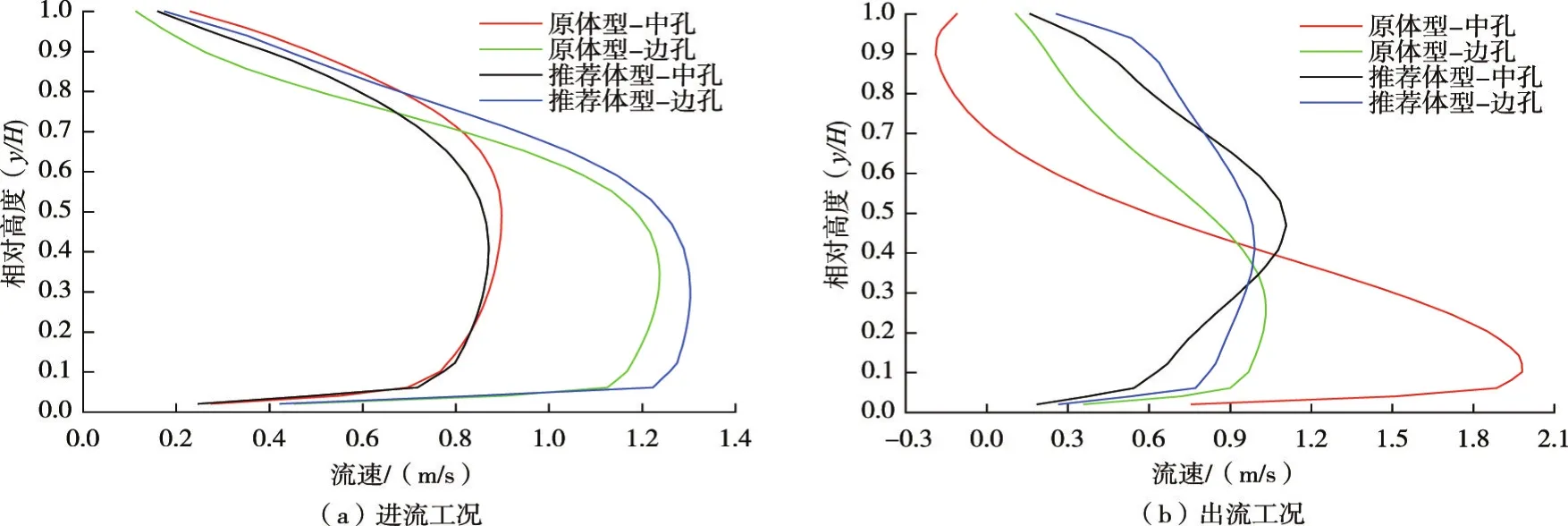
图7 原体型与推荐体型拦污栅断面中垂线的流速分布对比

图8 出流工况原体型与推荐体型4孔口拦污栅断面流速云图
5 结论
水工建筑物体型优化一般通过物理模型试验或数值模拟对设定体型进行水力特性研究,针对不利的水力指标调整体型再进行研究,直至获得满意的较优体型,这是传统的做法。双向水流条件下的侧式进/出水口的体型优化为多目标优化问题,本文将水力指标作为目标函数来得到最优体型。
(1)本文采用线性加权的方法将进流和出流工况下的水头损失系数合成为单一目标函数,即转化为单目标优化问题。同时选取流速不均匀系数和孔口间流量不均匀系数作为约束条件。多岛遗传算法具有较高的优化效率,对侧式进/出水口进行体型优化时能够得到最优体型。此外,参数化建模方法和基于CFD流场计算的响应面模型的应用,加快了方案比选中的建模与数值模拟速度。
(2)利用本文优化方法得到的推荐体型的各项水力指标较原体型有明显改善,双向水流条件下总水头损失系数降低3.35%,出流工况的孔口断面流速不均匀系数降低了14.50%,双向水流条件下的孔口间流量分配基本均匀,流量不均匀系数均小于20%。
[1]陆佑楣,潘家铮.抽水蓄能电站[M].北京:水利电力出版社,1992.
[2]孙双科,柳海涛,李振中,等.抽水蓄能电站侧式进/出水口拦污栅断面的流速分布研究[J].水利学报,2007,38(11):1329-1355.
[3]章军军,毛欣炜,毛根海,等 .侧式短进出水口水力试验及体型优化[J].水力发电学报,2006,25(2):38-41.
[4]张从联,朱红华,钟伟强,等.抽水蓄能电站进出水口水力学试验研究[J].水力发电学报,2005,24(2):60-63.
[5]高学平,叶飞,宋慧芳.侧式进/出水口水流运动三维数值模拟[J].天津大学学报,2006,39(5):518-522.
[6]高学平,李岳东,田野,等.抽水蓄能电站侧式进/出水口流量分配研究[J].水力发电学报,2016,35(6):87-94.
[7]张兰丁.响水涧抽水蓄能电站上、下库进(出)水口分流特性研究[J].水利水电科技进展,2010,30(6):48-52.
[8]蔡付林,胡明,张志明,等.双向水流侧式进出水口分流墩研究[J].河海大学学报(自然科学版),2000,28(2):74-77.
[9]杨小亭,张强,邓朝晖 .抽水蓄能电站进出水口模型试验[J].武汉大学学报(工学版),2007,40(1):66-68.
[10]沙海飞,周辉,黄东军.抽水蓄能电站侧式进/出水口数值模拟[J].水力发电学报,2009,28(1):84-88.
[11]陈南祥,李跃鹏,徐晨光 .基于多目标遗传算法的水资源优化配置[J].水利学报,2006,37(3):308-313.
[12]GAO Ting,WANG Yaxing,PANG Yongjie,et al.Hull shape optimization for autonomous underwater vehicles using CFD[J].Engineering Applications of Computational Fluid Mechanics,2016,10(1):601-609.
[13]孙斌,吕宏兴,宋晨光,等.基于Hicks-Henne型函数和MIGA的机翼形建筑物多目标水力优化[J].四川大学学报(工程科学版),2013,45(4):13-20.
[14]SERGIO Galvan,CARLOS Rubio,PACHECO Jesus,et al.Optimization methodology assessment for the inlet ve⁃locity profile of a hydraulic turbine draft tube:part II—performance evaluation of draft tube model[J].Journal of Global Optimization,2013,55(4):729-749.
[15]张乐,周洲,许晓平.飞翼布局无人机保形非对称S弯进气道设计及优化[J].航空动力学报,2016,31(11):2682-2690.
[16]马铁林,马东立,张朔.分析模型参数化建模在飞机多学科优化设计中的应用[J].航空学报,2008,29(6):1576-1580.
[17]倪计民,刘越,石秀勇,等.基于Doe分析的增压器涡轮叶形优化设计方法[J].农业机械学报,2016,47(7):361-367.
[18]JOURDAN Adrian,FRANCO Jonathan.Optimal Latin hypercube designs for the Kullback-Leibler criterion[J].Asta-advances in Statistical Analysis,2010,94(4):341-351.
[19]汪怡平,王涛,黎帅.基于自由变形技术的汽车气动减阻优化[J].机械工程学报,2017,53(9):35-143.
[20]ZHOU Liang,HAGHIGHAT Fariborz.Optimization of ventilation system design and operation in office environ⁃ment,Part I:Methodology[J].Building and Environment,2009,44(4):651-656.
[21]CHEN Hong,RYOZO Ooka,SHINSUKE Kato.Study on optimum design method for pleasant outdoor thermal en⁃vironment using genetic algorithms and coupled simulation of convection,radiation and conduction[J].Building and Environment,2008,43(1):18-31.
[22]WANG Kuowei,CHANG Lichiu,CHANG Fijohn.Multi-tier interactive genetic algorithms for the optimization of long-term reservoir operation[J].Advances in Water Resources,2011,34(10):1343-1351.
[23]KHALESI Nasrin,REZAEI Nazanin,HAGHIFAM Mahmoud-Reza.DG allocation with application of dynamic programming for loss reduction and reliability improvement[J].International Journal of Electrical Power and Ener⁃gy Systems,2011,33(2):288-295.
[24]赵德建,王延奎,周平,等.基于多岛遗传算法的二维翼型吸气减阻优化[J].北京航空航天大学学报,2015,45(5):941-946.
[25]辛馡,朱鳌鑫.遗传算法的适应度函数研究[J].系统工程与电子技术,1998(11):58-62.
[26]DL/T5208-2005抽水蓄能电站设计导则[S].北京:中国电力出版社,2005.

