数字激光散斑照相技术测金属杨氏模量

房 鑫，刘成森，张囡囡，赵琳琳，杨 瑶，孙娇月，彭金金，于国辉，宋嘉琦

(辽宁师范大学 物理与电子技术学院，辽宁 大连 116029)

在普通物理实验中，测量金属杨氏模量普遍采用光杠杆法. 该方法使用的光路较长，易受外界不稳定因素的影响，同时望远镜的小视场使实验调整比较困难. 一些研究人员提出用激光散斑照相技术测量金属杨氏模量，利用全息干板记录2次曝光的激光散斑图，干板在暗室下进行湿处理(显影、定影)[1-2]，然后用平行激光束照明干板记录的散斑图像，在夫琅禾费衍射区域获得干涉条纹，实验过程繁杂，无法进行自动化测量；同时由于条纹间距只能由米尺测量，测量费时、精度不高. 本文利用数字记录器件(电荷耦合元件CCD)连续拍摄激光散斑图像，经计算机处理得到2次曝光的散斑干涉条纹，从而计算出相应的金属细丝伸长量，实现了计算机控制下的自动化测量，该方法光路简单、仪器紧凑、实验过程稳定连续.

1 实验原理

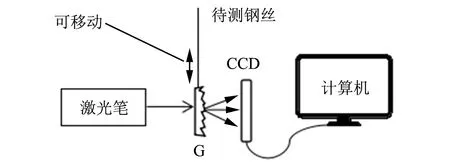
图1 实验原理图

当激光照射物体的漫射表面(如纸张、未抛光的金属表面、混凝土表面等)，或通过透明的漫射体时，会在其表面以及附近空间产生无规则分布的亮暗斑纹，即激光散斑[3]. 将毛玻璃作为漫射体，建立图1的光路(G为毛玻璃)，设毛玻璃与CCD之间的距离为f，调整f找到最佳像平面，用CCD接收并用计算机记录，得到1张散斑图像，在其他条件不变的前提下，给钢丝加重，毛玻璃随着钢丝的变化而移动，用计算机记录，得到第2张散斑图，缓慢均匀地给钢丝加重，得到一系列连续变化的散斑图，依次选取相邻的2张散斑图，用计算机模拟夫琅禾费衍射，分别得到几组等间距的干涉条纹[3-5]. 条纹间距为x(其中ΔL′为钢丝的微小位移量),有

(1)

根据杨氏模量公式

(2)

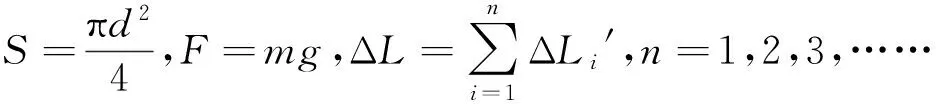
(3)

式中,F为钢丝产生形变时所加的外力，m为钢丝产生形变时所加的质量，L为钢丝原长度，S为钢丝横截面积，ΔL为钢丝伸长量,d为钢丝直径.

2 实验内容及实验结果

实验时，将杨氏模量测定仪(加重范围为0～30.0 kg)置于稳定的光学平台上，如图2所示，激光束打在毛玻璃上用CCD承接，先给钢丝加重10.0 kg使钢丝拉直，用米尺量取此时钢丝的长度作为钢丝原长,用螺旋测微仪量取钢丝直径d,在10.0 kg的基础上给钢丝加重，同时用CCD连续采集移动的散斑图，共采集7张连续变化的激光散斑图. 图3分别为采集到的加重为13.0 kg和16.0 kg的数字激光散斑图.

图2 实验实物图

图3 数字激光散斑图

用计算机选取加重为13.0 kg和16.0 kg的数字激光散斑图，将2张散斑图像的光强叠加，做傅里叶变换得到如图4的夫琅禾费衍射图，将图4中干涉条纹光强沿着横向叠加得到条纹强度分布曲线，对其进行中值滤波处理[7]，获得如图5的光滑的条纹分布曲线图(图中ξ轴为沿着移动方向频谱平面的坐标轴)，在图5上选取2个连续的峰值，峰值横坐标之差即为2个条纹的间距x,根据式(1)计算出金属细丝相应的微小位移量ΔL′，依次用计算机选取相邻的激光散斑图像，重复上述处理过程，得到表1的实验数据.

图4 夫琅禾费衍射图

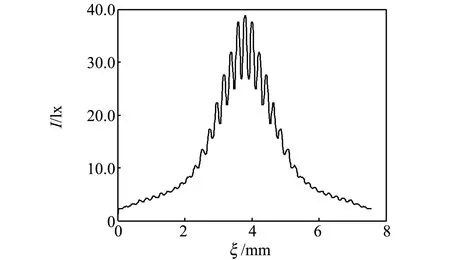
图5 条纹强度分布曲线

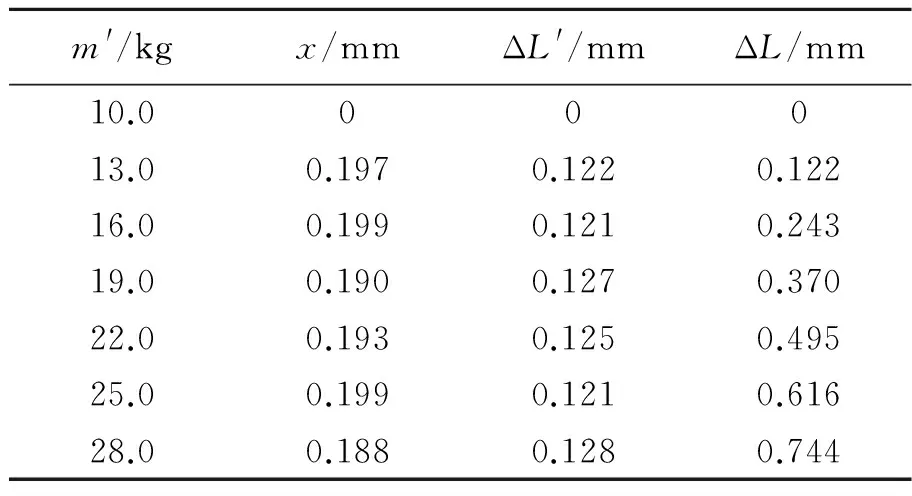
m'/kgx/mmΔL'/mmΔL/mm10.000013.00.1970.1220.12216.00.1990.1210.24319.00.1900.1270.37022.00.1930.1250.49525.00.1990.1210.61628.00.1880.1280.744

实验中的相关参量为：L=40.50 cm,d=0.800 mm,f=3.80 cm,λ=635 nm,CCD像素尺寸Δ=10.0 μm.m为钢丝产生形变时加的质量

m=m′-10.0 kg

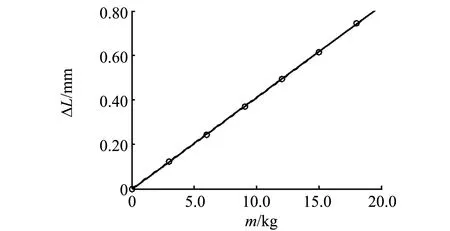
图6 m-ΔL关系图

用计算机对m和ΔL数据进行线性拟合，拟合斜率k=0.041 3,得到图6. 根据式(3)可得

(4)

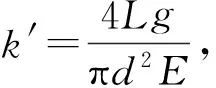
ΔL=k′m,

(5)

由k′=k=0.041 3求得

E=1.95×105N/mm2.

由式(3)和式(5)结合不确定度的传递公式得到杨氏模量的不确定度[6]为

(6)

xj={L,d,k}，uj为对应变量的不确定度，L和d只测量了1次，因此选取L和d的B类不确定度

其中米尺和螺旋测微仪的仪器误差限分别为ΔL=0.5 mm，Δd=0.004 mm，结合图6得到uk≈0，代入式(6)得杨氏模量的不确定度uE≈0.01×105N/mm2. 故实验测得的杨氏模量值为

E=(1.95±0.01)×1011N/m2.

3 结束语

该测量杨氏模量的方法，利用CCD和计算机快速自动的采集和处理数字激光散斑图，保证了测量过程的连续稳定. 利用光学干涉技术的高精度的特点，提高了测量精度. 数字激光散斑技术操作简单，受外界因素影响小，在实验教学中体现了现代的科技手段，具有广泛的应用前景和实用性，这种原理还可用于其他微小位移量的测量.

[1] 张存恕，李德宽. 用激光散斑法测金属的杨氏模量[J]. 物理实验，1983，3(3):97-102.

[2] 李淑春. 用激光散斑测微小位移及应用[J]. 中国民航学院学报，1994，12(3):104-107.

[3] 吕乃光. 傅里叶光学[M]. 北京：机械工业出版社，2006:357-375.

[4] 李晓英，郎晓萍. 激光散斑位移测量方法研究[J]. 北京机械工业学院学报，2008,23(1)；39-61.

[5] 姚启军. 光学教程[M]. 北京：高等教育出版社，2008:16-18.

[6] 贾永红. 数字图像处理[M]. 武汉：武汉大学出版社，2015：77-79.

[7] 徐勋义，张祖豪，刘子健,等. 基于迈克耳孙干涉的金属丝杨氏模量测量[J]. 物理实验，2016,36(9)；19-22.