引导发现后的验证不可少

◇陈励群

案例一：“有余数的除法”教学片段

师：用竖式计算： 47÷5，20÷3，54÷8，35÷9。通过计算你发现了什么？

生：通过计算，我发现这几道题都有余数。

生：我发现这几道题的除数都比余数大。

生：我发现这几道题的余数都比除数小。

师：同学们真聪明，自己发现了有余数除法的计算规律——余数一定要比除数小。

（教师板书结论）

师：齐读一遍。

师：判断下面的计算是否正确，为什么？

38÷6=5……8， 45÷5=8……5，26÷4=5……6。

生：这三道题都错了，因为余数要比除数小，而这三道题的余数都比除数大。

……

案例二：“3的倍数的特征”教学片段

师：我们一起回忆一下2、5的倍数的特征。

生：个位上是 0、2、4、6、8 的数是 2 的倍数，个位上是0、5的数是5的倍数。

师：猜一猜，一个数是不是3的倍数，我们是不是也只要看这个数的个位上的数呢？

生：我觉得一个数的个位上是3、6、9的，这个数就是3的倍数。

生：我有不同的意见，19个位上的数是9，但19就不是3的倍数，21个位上的数是1，但它是3的倍数。

生：我觉得一个数是不是3的倍数不能只看个位上的数是多少。因为我写了10个3的倍数：3、6、9、12、15、18、21、24、27、30。 发现个位上是0、1、2、3、4、5、6、7、8、9 的数都有可能是 3 的倍数。

师：请同学们四人一组拿出计数器，在计数器上分别拨出几个3的倍数，看看各用了多少个珠子。小组再讨论一下，看有没有什么发现。

生：我们组发现，如果一个数是3的倍数，所用的珠子的个数也是3的倍数。

生：我们组发现，如果一个数不是3的倍数，它所用的珠子的个数就不是3的倍数。

生：我们组发现，一个数是不是3的倍数与它各个数位上的数都有关系。

在教师的引导下，学生发现了3的倍数的特征：一个数各个数位上数的和是3的倍数，这个数就是3的倍数。

师：在 29、45、51、67、86、96 中，哪些是 3 的倍数？

……

案例三：“圆的认识”教学片段

在学生理解了圆的特征后出示课本第90页的第8题：

（1）指出下边圆里的线段哪一条是直径。（如图1）

图1

（2）量一量这几条线段的长度，你发现了什么？

（3）互相说一说为什么可以用下面的方法（如图2）测量圆的直径。

图2

生：我发现在圆里的线段中，直径最长。

生：因为，圆里的线段中，直径最长，所以可以用上面的方法测量圆的直径。

……

思考：上述三个案例，教师在引导学生发现规律后，没有引导学生去验证甚至证明规律的正确性，而是让学生机械地记住规律，直接运用规律解题。这样的教学不利于学生深刻理解所学的知识，不利于学生形成科学严谨的学习态度和良好的思维习惯。这种只让学生发现“是什么”，而不引导学生深究“为什么”，不引导学生验证甚至证明发现的结论是否正确的教学，在课堂教学中屡见不鲜。究其原因，可能部分老师认为：（1）小学生的知识水平较低，难以说清楚“为什么”；（2）只要发现的规律是正确的，验证或证明这个环节要不要无所谓。事实上，很多数学规律和一些结论，学生是能够讲清“为什么”的。

如案例一，只要让学生动手摆摆实物或学具，他们就很容易理解“余数为什么要比除数小”。

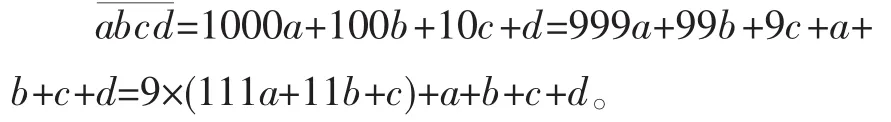
可以看出，9×(111a+11b+c)必定是3的倍数，所以判断是不是3的倍数，就只看a+b+c+d能否被3整除，也就是看它各个数位上的数之和是不是3的倍数。

当然我们也可以引导学生用除法来验证：把这个数分解成整百、整十数，分别除以3，看是否有余数。以486为例，要判断它是不是3的倍数，可以从这个数的高位除起，先用4个100除以3，每个100都余1，共余4，正好就是百位上的数“4”。同样道理，8 个 10 除以 3，每个 10 都余 1，共余8，正好就是十位上的数“8”，个位上还有6，将余下来的数相加，4+8+6=18，18除以3，没有余数，所以486是3的倍数，因此一个数是不是3的倍数就要看它各个数位上的数之和是不是3的倍数。

案例三中，要使学生理解圆中直径最长，只要将非直径线段的两个端点分别与圆心连接形成一个三角形 （如图3），根据三角形的三边关系，两条半径的和（也就是直径的长度）肯定大于圆里的任何一条非直径线段，所以直径是圆里最长的线段。

图3

因此，老师在引导学生发现规律后，应该相信学生的能力，给学生一定的时间，让学生去思考、深究、理解“为什么是这样的”。这样的验证或证明是不能少的。