以形助数理解小数的意义

◇闫金艳

一 利用图形帮助学生走出认知误区

在“小数的意义（一）”（北师大版教材四年级下册第一单元，下同）一课中，我以元、角、分为切入点，利用正方形面积模型直观地表示1角和1分，通过分数理解小数的意义（如图1）。

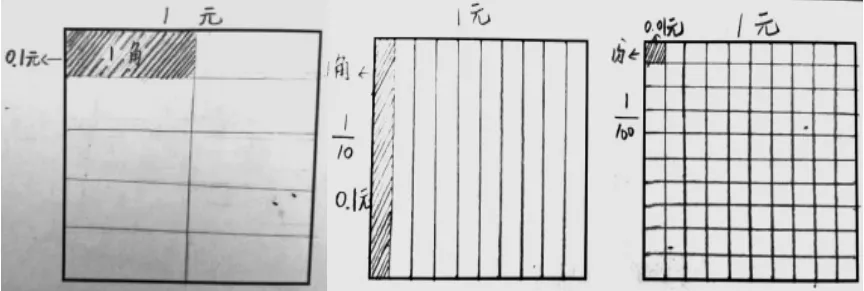
图1

当问学生“你还想用这个正方形表示什么？分一分，其中的1份表示什么”时，学生的想法太丰富了。一个学生说，我把这个正方形看成一块大蛋糕，把它平均分成6份，其中1份就是0.1块蛋糕。（如图2）

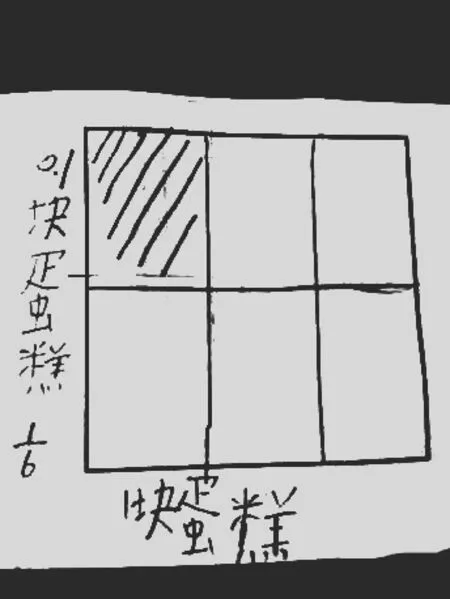
图2

学生的认知误区在哪儿？原来学生受元、角、分转化成小数教学的负迁移，认为蛋糕中的1份也是0.1。看来学生对0.1记忆深刻，忽略了小数的十进制关系。学生有学习分数的经验，把一个整体平均分成若干份，取其中的1份可以用几分之一表示，自然认为在小数里面也是这样，平均分后取其中的1份就是0.1。又如有的学生用时与分的关系来表示0.1（如图3）。学生知道1小时是60分，因此，他们认为把1个正方形平均分成60份，取其中的1份就是0.1小时。

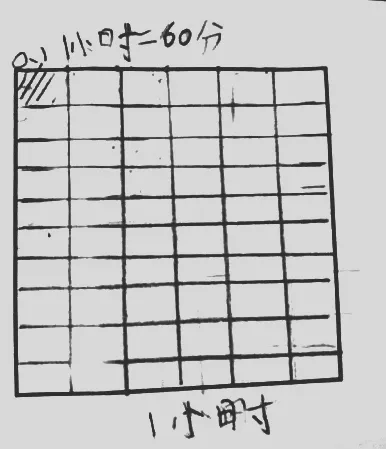
图3

对小数意义的理解，为什么学生存在这么大的困难？学生的认知误区恰恰是我们课堂上教学该用力的地方，该怎样设计教学以帮助学生厘清认识呢？我进行了一次教学尝试。

【片段 1】

教师先利用数线直观图，带领学生思考怎样以米为单位，用分数形式表示1分米、1厘米、1毫米，完整地经历一位小数、两位小数、三位小数的产生和发展过程，之后出现正方形的直观图。

师：刚才我们把1米平均分成10份、100份、1000份，从而认识了 0.1米、0.01米、0.001米（如图 4）。

图4

师：如果以元为单位，你能在表示元的正方形中分一分、涂一涂找到0.1元和0.01元吗？

师：请同学们观察表示0.1米的数线和表示0.1元的正方形图，你们有什么发现？

（学生合作学习，完成学习任务）

这样设计问题的目的在于帮助学生建立十进分数与小数之间的关系，如与 0.1，它们不是不同的两个数，而是同一个数的不同形式，表示的意义是相同的。这样的环节设计后再让学生用这个正方形分一分，问学生“你还能用其中的1份表示什么”时，学生就能清楚地走出块蛋糕是0.1块蛋糕、1分是0.1小时等认知误区。

二 沟通形与形之间的联系，帮助学生理解小数的意义

整数和小数有很多相同的规律。如在整数的两个相邻的数位之间，左边数位的位置值都是右边的10倍。不同点则是计数单位发生变化。学生受整数认识的影响往往误认为以小数点为分界，整数部分从右往左计数单位越来越大，小数部分就会从左往右计数单位越来越大，呈现对称现象。

在“小数的意义（三）”一课中，教材用计数器和数位顺序表，帮助学生认识小数各个数位的位值意义。在教学中，我大胆尝试，运用数线、正方形、正方体和计数器四种直观模型，沟通它们之间的联系，帮助学生理解和掌握小数数位顺序表，认识小数各个数位的计数单位及其进率关系。

【片段 2】

教师出示数线、正方形、正方体，并指出：我们可以用整数1表示数线上0到1之间的距离，也可以用正方形的面积或正方体的体积表示1，那么，你能用它们分别表示出 0.1、0.01、0.001吗？你从中有什么发现（如图5）？

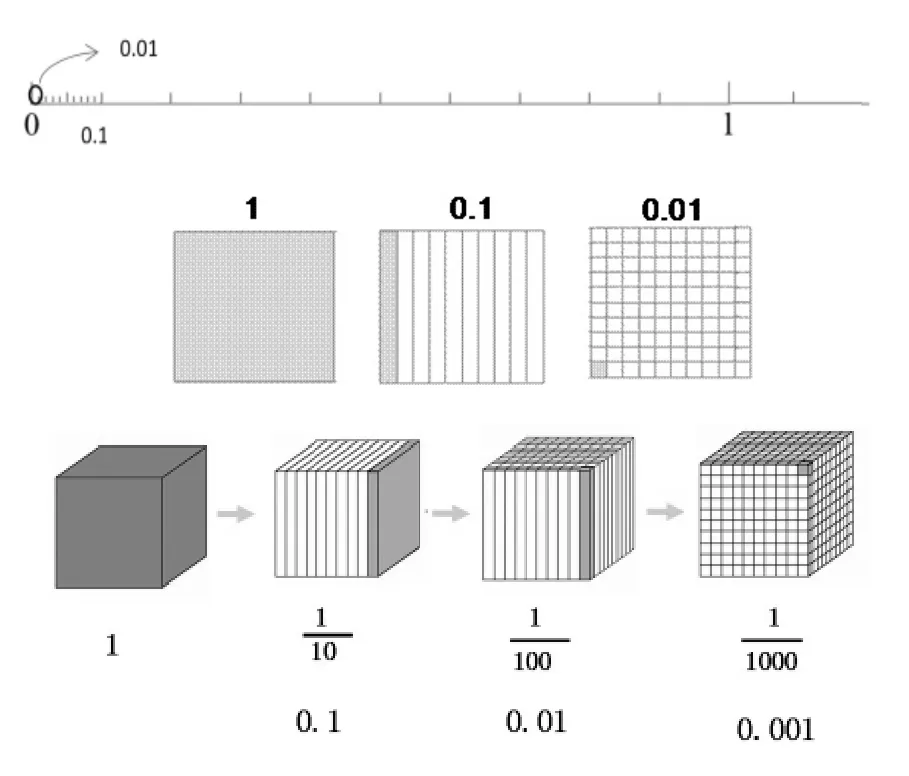
图5

生：我发现虽然分数的分母越来越大，但是与分数相等的小数越来越小，越来越接近0。

师：也就是说小数部分的计数单位越来越小。

生：我还发现小数部分相邻两个计数单位之间的进率也是10，与整数部分的进率相同。

师：看来小数的计数单位与整数一样，也是“满十进一”，即小数相邻计数单位之间也具有十进关系。

接着教师出示计数器和数位顺序表，把整数的十进位值制原理推广到小数。

小数的出现源于人们对精确度的要求，小数的发展是不断细分、不断追求更高精确度的必然结果。直观图形让小数的意义变得直观明了，可帮助学生积累丰富的感性认识，为学生顺利抽象概括小数的意义奠定了基础。