改进的基于结构元的模糊网络计划计算模型
蒋红妍, 布亚军, 张小玲
(西安建筑科技大学 土木工程学院, 陕西 西安 710055)
模糊网络计划技术是在传统网络计划的基础上衍生出来一种考虑实际项目中存在不确定因素的一种网络计划技术。目前,关于模糊网络计划时间参数的计算问题,主要采用模糊数进行运算。由于模糊数排序与运算问题的复杂性与不可逆性,使得模糊网络计划时间参数计算相对比较困难。自2002年,郭嗣琮提出了模糊结构元分析方法后,刘海涛、杨皎平、赵宏霞等基于模糊结构元分析方法先后解决了模糊数排序以及模糊数运算不可逆的问题[1~4]。随后,于慧敏在其论文中系统介绍了基于结构元理论的模糊时间参数计算公式,并对模糊网络工期-成本进行了优化[5]。
虽然以上学者通过模糊结构元理论克服了模糊网络时间参数计算的缺陷,简化了模糊网络计划时间参数的运算,但在实际项目中,尤其是在建设项目的每个单元各个工序不断重复进行的项目(重复性项目)[6]中,学习效应现象的出现也影响着模糊网络计划的制定。学习效应即当个人或组织重复地生产某一产品时,单位产品所需的时间(成本)会随着产品数量的增加而逐渐减少的现象[7]。如今建设行业,重复性项目十分常见,学习效应对工程项目网络计划的影响也越来越不容忽略。在模糊网络计划中考虑学习效应对模糊工期的影响是必要的。
本文针对模糊结构元理论在模糊网络计划计算方面的不足,基于实际工程中存在的“学习效应”现象,提出了改进的基于结构元理论的模糊网络计划计算模型。在此基础上通过案例验证计算模型,对模糊网络计划时间参数的计算具有指导意义。
1 基于结构元的模糊网络计划计算模型
基于结构元的模糊网络计划计算模型主要通过定义模糊数大小比较以及模糊数减法运算来克服模糊数计算过程中的缺陷。本章介绍传统的基于模糊结构元的网络计划计算模型的基本理论。
1.1 三角模糊数相关概念
为方便计算,本文采用三角模糊数表示项目中工序工时的不确定量。隶属度函数如图1那样的模糊数N=(a,b,c)称为三角模糊数。

图1 三角模糊数隶属函数
其隶属度函数表示如下:
图中a,b,c三点分别代表工序工时在最乐观、最可能、最悲观情况下的取值。
1.2 结构元理论
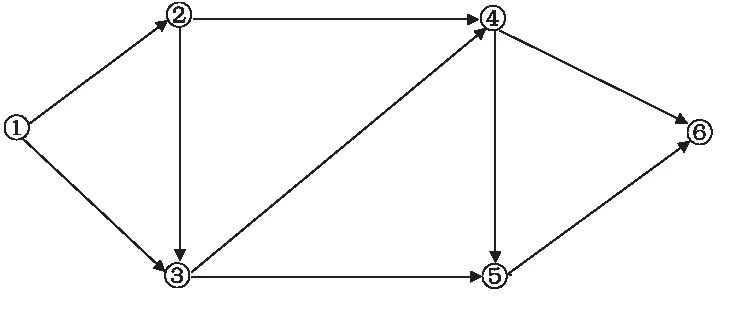
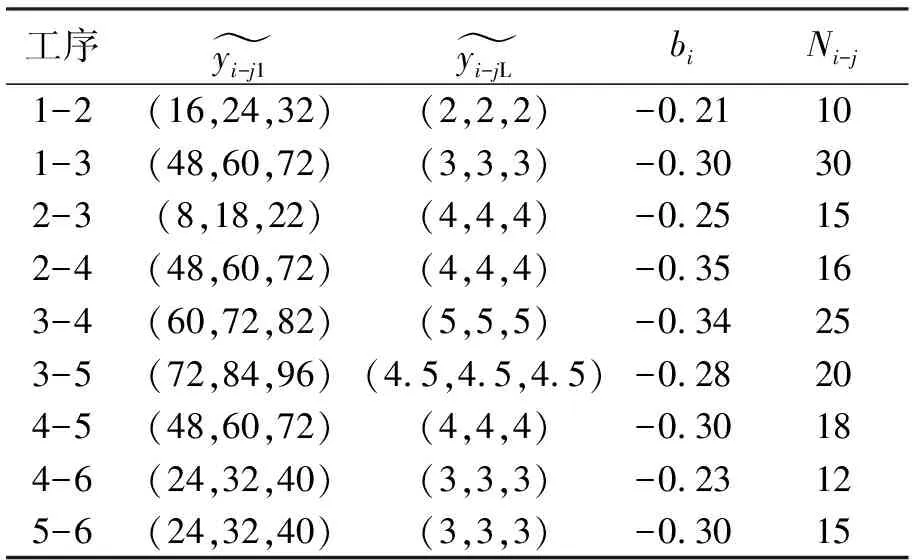
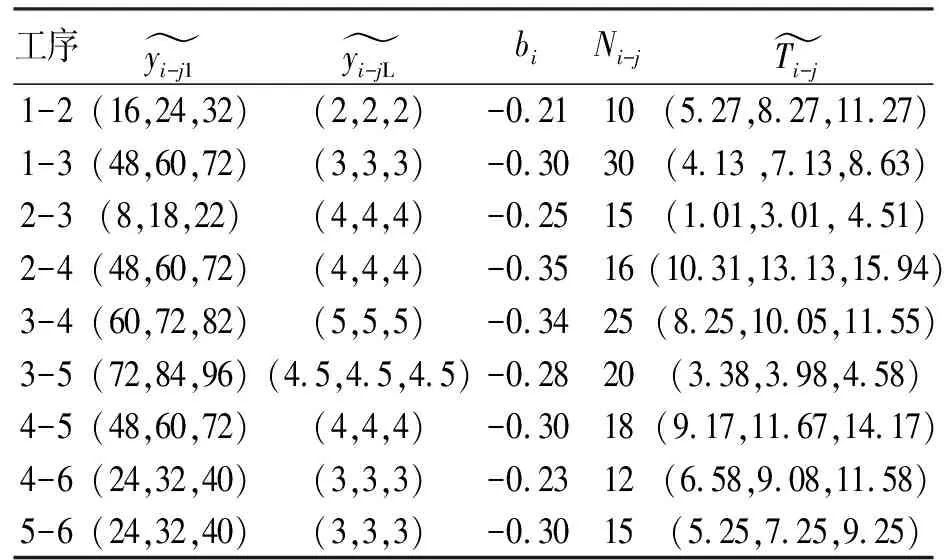
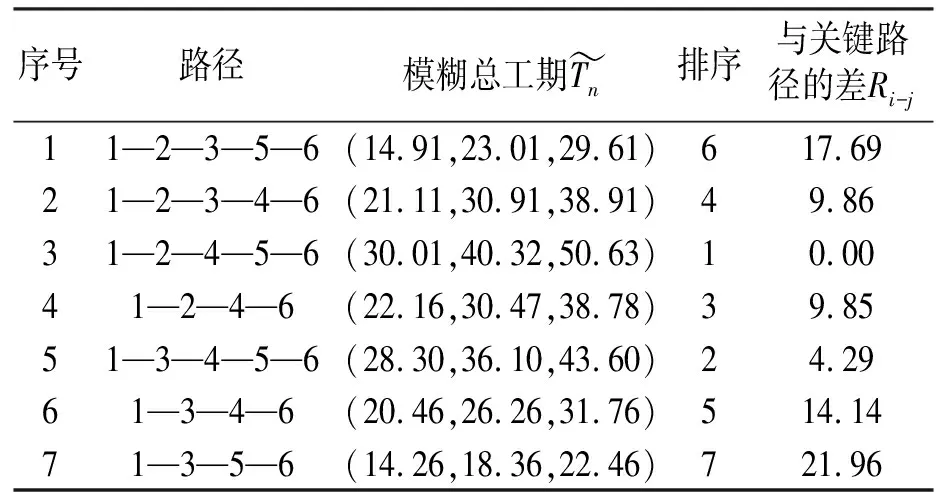
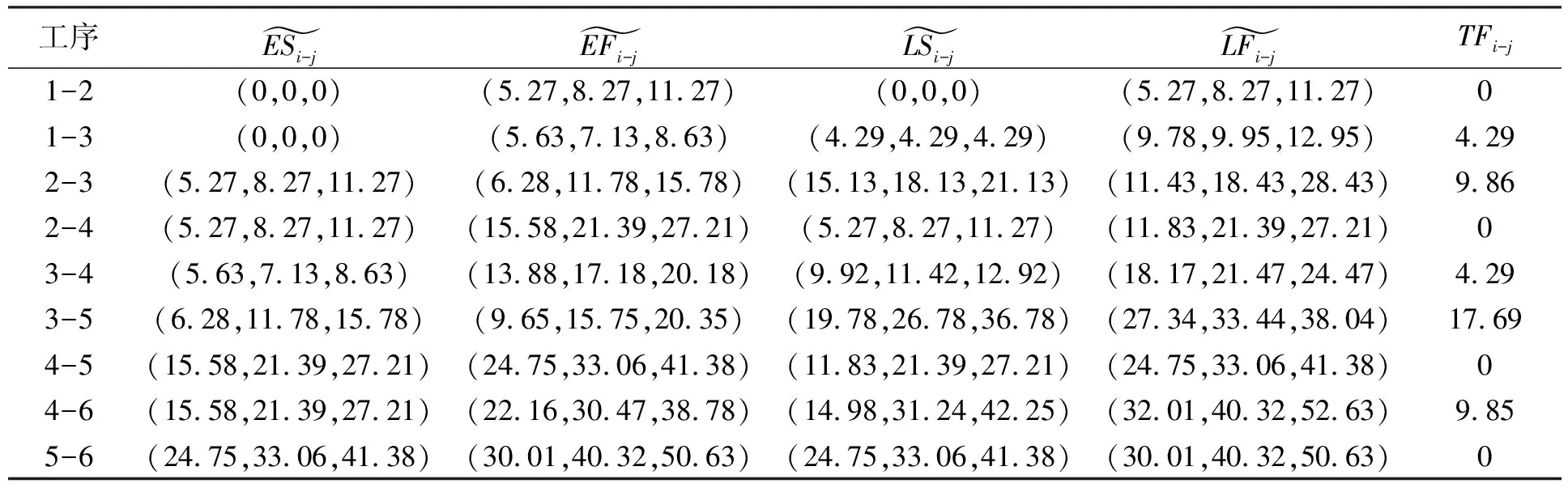
定义1[8]:设E为实数域R上的模糊集,隶属函数记为E(x),x∈R。如果E(x)满足下述性质:(1)E(0)=1,E(1+0)=E(-1-0)=0;(2)E(x)在区间[-1, 0)上是单增右连续函数,在区间(0, 1]上是单降左连续函数;(3)当- 根据定义,模糊结构元是R上的正规凸模糊集,即是一个模糊数,并且是有界闭模糊数。它是表示模糊零概念的特殊模糊数,可以具有各种形态。 对于模糊数大小比较在模糊数学上的定义,往往两个模糊数比较大小得到的是一个新的模糊数,而不是两个模糊数的一个。于慧敏[5]根据模糊结构元理论提出了新的模糊数大小比较的定义。 定义2[8]:设E是模糊结构元,模糊数A=f(E),B=g(E),如果 通过此定义将模糊数之间模糊比较关系转化为确定数之间的比较关系,克服了传统模糊数大小比较方法的弊端,同时可以解决模糊网络计划中关键路线确定问题。 传统模糊数四则运算中,模糊数加法和减法是不可逆的,这就导致在模糊网络最迟时间参数计算时可能出现负值。模糊结构元理论的提出恰恰能够解决这一问题。 定义3[5]:设E是模糊结构元,f和g是[-1,1]上两个单调函数,模糊数A=f(E),B=g(E),C=h(E),若B+C=A,则定义A-B=C。即 通过此定义,将模糊数减法运算转化为加法运算的逆运算,在计算模糊网络计划模糊最迟时间参数时避免了出现负值的情况。另外本文在计算时将总时差设定为确定数,即特殊的模糊数,这与实际情况也是相符的。 二十世纪二十年代,Wright[9]首次命名了学习效应,将其定义为随着产量增加,生产单个产品的时间会逐渐降低的现象。自学习效应提出以来,国内外学者对学习效应展开了诸多研究,并将其应用在多个领域。综合国内外关于学习效应的文献不难发现,学习效应对工程项目工期的影响较大,是制定网络计划不可忽略的重要因素,在制定网络计划时考虑学习效应的存在,可以节省人力、财力,更加有利于项目管理。在对学习效应进行实证研究后,王鑫业创新性地提出了两阶段学习模型,改善了已有的学习曲线模型预测性能欠佳的不足[10]。本文在研究了两阶段模型后认为该模型更加贴合国内项目实际情况,因此在网络计划计算中考虑学习效应的因素,用两阶段学习曲线模型表示工序工期。 在确定性情况下,两阶段学习模型表示如下: 式中:yix为工作i在单元x上的计算累计平均工时;yi1为工作在第1个单元上的工时;yiL为由于学习效应显现,工作i可节约的工时;bi为-1到0之间的常数,1-2bix反映了工作学习效应显现的快慢,bi值越小说明学习效应显现地越快;X为总的重复单元数。 在实际工程项目中,由于天气、环境等原因的影响,实际工时是不确定的,为了方便计算,本文采用三角模糊数来代表模糊工时。另外为了与以下模糊网络计划计算工序时间对应,将工作i用工序i-j替换,所以在不确定条件下的两阶段学习曲线模型可以记为: 由以上模型可以推出工序i-j总的模糊工期为: 式中:Ni-j为工序i-j在重复单元上的平均操作者数量。 (1) (2) (3) 当Dp(i)=Ø时, (4) (5) (6) (7) 即 TFi-j=Ri-j (8) (9) (10) 某高层混凝土住宅项目,其所有工作在30层之间不断重复,根据文献10中总结的施工中存在学习效应的必要条件,现取其中6道工序,其网络图如图2所示,基于施工经验得到各个工序的学习效应参数值如表1。求每个工序的模糊时间参数以及关键路径。 图2 模糊网络示意 工序yi-j1yi-jLbiNi-j1-2(16,24,32)(2,2,2)-0.21101-3(48,60,72)(3,3,3)-0.30302-3(8,18,22)(4,4,4)-0.25152-4(48,60,72)(4,4,4)-0.35163-4(60,72,82)(5,5,5)-0.34253-5(72,84,96)(4.5,4.5,4.5)-0.28204-5(48,60,72)(4,4,4)-0.30184-6(24,32,40)(3,3,3)-0.23125-6(24,32,40)(3,3,3)-0.3015 采用传统的基于结构元的模糊网络计划计算模型得到的关键路1—2—4—5—6,模糊计算工期为(33.25,43.56,53.88)。采用改进的模糊网络计划计算模型的计算过程如下: (2)对网络计划中各个路径进行排序,求出各个路径与关键路径的差Ri-j,如表3所示。 (3)根据基于学习效应及结构元理论的模糊网络计算模型得到各个工序的时间参数,如表4。 表2 学习曲线模型参数值 表3 各个路径的模糊总工期即排序 表4 各工序模糊时间参数 得到关键路径为1—2—4—5—6,模糊计算工期为(30.01,40.32,50.63)。 由结构元理论可得(33.25,43.56,53.88)和(30.01,40.32,50.63)转化为模糊结构元分别为: 比较两种方法得到的结果,虽然关键路径相同,但在工期方面,改进的模糊网络计算工期比未考虑学习效应的工期小。 在现有的资料中,对模糊网络计划的研究多集中在求解关键路径与时间参数上,在基于结构元的模糊网络计算模型的基础上考虑学习效应对模糊工期的影响是一个创新。本文先将确定性条件下的两阶段学习曲线模型转化为模糊两阶段学习模型,再与基于结构元理论模糊网络时间参数计算模型相结合,得到改进的模糊网络计划时间参数计算模型。最后通过一个小案例,分别从单纯基于结构元理论的计算和将学习效应与模糊结构元相结合两方面求解关键路径与模糊时间参数。通过本文的研究,验证了学习效应对模糊网络计划工期的影响,以及改进的结构元理论模糊网络计算模型的实用性,为其它重复性项目制定模糊网络计划提供了依据。在实际工程应用中,一方面考虑施工中的不确定性因素以及学习效应现象的存在,为进一步模糊网络计划优化提供了基础;另一方面,模糊网络计划技术的应用可以对工程项目进度管理做进一步指导。但是本文在确定模糊网络计划关键路时默认最长路即关键路,完工工期等于最长路长度,而没有考虑不确定条件下网络计划与经典网络计划在逻辑关系上的不同。因此,在以后的研究中可以从逻辑分析方法对模糊网络关键路进行分析。1.3 基于模糊结构元定义的模糊数大小比较



1.4 基于结构元理论的模糊数减法运算



2 改进的基于结构元的模糊网络计划计算模型
2.1 不确定条件下的两阶段学习曲线模型
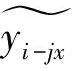
2.2 改进的模糊网络计算模型
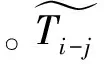
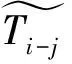
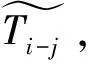

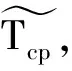
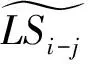
3 实 例
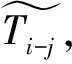

4 结论与展望

