应用自适应差分进化算法优化测试数据研究
李龙澍,翁晴晴
(安徽大学 计算机科学与技术学院,合肥 230601)
1 引 言
软件测试是测试人员对开发人员所开发的软件进行测试,尽可能多地发现软件中存在的错误,以保证开发人员所开发的软件正确且没有潜在的缺陷.因此软件测试是软件开发周期中非常重要的环节[1].
遗传算法作为传统的用于生成软件测试数据的算法,其应用范围非常广泛[2].但传统的遗传算法通常表现出收敛速度慢,易陷入局部最优等缺陷.近几年有人提出通过将遗传算法与蚁群算法或粒子群优化算法等智能算法相结合的方案[3],用以提高算法效率.但是遗传算法和PSO算法参数过多,不同的参数设置对最终结果影响较大,因此在实际应用中,需不断调整,加大了算法的使用难度.自适应差分进化算法[4,5]仅需调整缩放因子F与交叉概率Cr,且可以自动调节缩放因子和交叉概率,能够更加有效地提高收敛速度及防止陷入局部最优.与其他进化算法相比,自适应差分进化算法相对简单,且能够快速收敛到最优值附近.因此,本文对自适应差分进化算法进行改进,并用于测试数据的产生.
Storn和Price[6]首次提出差分进化算法,该算法相对简单而且可以直接针对实数进行寻优.目前,差分进化算法已广泛应用于解决目标优化问题,如带约束的优化问题[7],多目标优化问题[8]和工程设计优化问题[9]等.但是,差分进化算法的控制参数需要根据先验知识提前设置,不够灵活.针对以上问题,不同的适应性差分进化算法相继被提出[10-12];其中,Zhang 和 Sanderson[10]提出的自适应性的差分进化算法(JADE),利用上一代优越个体的缩放因子和交叉概率来更新当前每个个体的控制参数,很好地防止算法进入早熟,并且大大增强了算法的灵活性.但是,JADE的变异策略是从100*p%(p为概率)种群中随机选取一个个体取代当前最优个体,降低了差分进化算法的收敛速度.
通过对差分进化算法的研究发现,差分进化算法的性能与其变异操作有很大关联.本文所提出的基于质心的自适应差分进化算法(Adaptive Differential Evolution based on Center of Mass,CADE)用以生成软件测试数据的方法,不仅通过扩充种群中个体的多样性,避免算法进入早熟;而且通过加快种群收敛速度的方式,降低了自动产生测试数据所需时间.同时,利用质心原理寻找最优值的策略,实现整体上平衡全局与局部的搜索能力.最后,通过仿真实验表明该方法在收敛速度和搜索精度上均有明显的优势.
2 基本概念
自适应差分进化算法是贪婪性遗传进化算法,主要包含种群初始化、变异、交叉及选择阶段;其利用多个个体的差分信息作为个体的扰动量,使得算法在跳跃距离和搜索方向上具有自适应性.在自适应差分进化算法中,变异操作对种群的进化方向起着决定性作用[13].自适应差分进化算法种群的初始化及变异操作如下:
1)种群初始化
在自适应差分进化算法中,设t表示进化代数,NP表示种群规模,D表示个体的维数,Xt表示第t代种群.首先,在问题的决策空间内随机产生第0代种群:X(0)=x1(0),x2(0),…,xNP(0).其中,xit是第t代种群中第i个个体.个体每一维上的取值可按下式产生:xi,j(0)=Lj+randi,j0,1(Uj-Lj),Lj,Uj第j维的取值范围,其中1≤i≤NP,1≤j≤D;randi,j0,1为介于0和1之间的一个均匀分布随机数,其中j∈1,2,…,D.
2)变异
在每一代t中,都会根据当前种群产生变异向量Vit.现有的变异操作有很多种,主要包含如下几种:
DE/rand/1Vi(t)=xr1(t)+Fi(xr2(t)-xr3(t))
(1)
DE/best/1Vi(t)=xbest(t)+Fi(xr1(t)-xr2(t))
(2)
DE/current-to-pbest/1Vi(t)=xi(t)+Fi(xpbest(t)-xi(t))+Fi(xr1(t)-xr2(t))
(3)
其中:Fi为自适应DE中每个个体的缩放因子,取值范围为0,1.xr1t,xr2t和xr3t是从集合1,…,NPi中随机选择的相互不同的个体,xpbestt为当前种群中最优个体.
3 CADE
3.1 差分进化算法改进
由于变异策略的选择对差分进化算法的效率有着极大的影响.因而对差分进化算法的改进一般都是针对变异策略的改进[14].现在改进的方法主要有自适应的缩放因子Fi的引入、对于缩放个体的选择标准等,相应的实验效果都表现出较快的收敛速度及较高的收敛精度.
A)由第二节的变异算子公式我们可以看出,种群中个体间差分向量的大小受缩放因子Fi取值的影响,缩放因子Fi的取值越小,相应的扰动也就越小.这就意味着,在差分算法的初始阶段,由于个体间彼此差值较大,扰动也较大,算法能够在较大的范围内进行搜索;而在算法的后期,群体间个体都逐渐向最优个体靠拢,进而扰动值降低,使得算法得以在较小的范围内进行搜索.但是传统的Fi值都是依据先验知识人为设定且固定不变的,在后期向最优值收敛时效果不是很好,因此研究者通过引入不同的自适应方法和自适应机制动态地更新控制参数,来提高算法性能.
B)在差分进化算法的变异阶段,已有很多对引入物理学中质心这一概念的研究,如Das等人[15]提出的AnDE算法中就使用质心这一概念,并在变异阶段将求得的新个体作为变异值代替当前全局最优值.在实验中,算法较传统的差分进化算法表现要好.物理学中质心计算公式如(4)所示:

(4)
其中,rδ为所求的质心(center of mass),mi是第i个粒子的质量,ri是第i个粒子所对应的具体值.
但是就目前研究来看,已有的方法都是假设种群中各个粒子质量相同,并未考虑到各个粒子之间的差异性,所以本文对质心的应用做出改进,在已有的JADE算法的基础上,提出了一种基于质心的变异算子.改进后的变异算子为:
Vi(t)=xi(t)+Fi(xwBest(t)-xi(t))+Fi(xr1(t)-xr2(t))
(5)
其中,xit,xr1t和xr2t为随机选择的互不相同的个体.Fi使用JADE中的方式确定.
3.2 xwbest的选择标准
A)最佳质心个体BCoI(the Best Center of Individual)
BCoI(t)=(BCoI1,BCoI2,…,BCoIn,…,BCoID)
(6)
其中,BCoIt是一个D维向量,即我们通过质心求解方式得到一个新的个体.
在第t代种群中,根据下式求得BCoI第n维元素的值:

(7)
其中,n表示BCoI(t)中第n维,N表示从第t代种群中随机抽取100*p%(p为概率)个个体,fit表示对应xi个体的适应度值,fsum表示N个个体适应度值之和.
由公式(7)求得BCoI的值将个体适应度值考虑在内,也将种群的进化方向考虑在内.不同个体适应度值不同,因此重要性也各不相同.由此赋予每个个体不同的权重值,偏离最优值方向的个体权重较小,靠近最优值的个体则权重较大,因此求得的BCoI更趋于最优值.
B)全局最佳质心个体GBCoI(the Global Best Center of Individual)
当前种群中求得的BCoIt适应度值可能优于上一代种群的全局最佳质心个体GBCoI(t-1)适应度值,也可能低于其适应度值.为保证种群能够向最优值方向进化,本文根据公式(8)选出全局最佳质心个体:

(8)
由公式(8)所得的新个体GBCoIt适应度值可能比当前种群的全局最优值xbest低,也可能优于全局最优值xbest,所以本文定义以下规则选出用于变异的最优个体,即xwbest:

(9)
根据公式(9)计算得出的xwbest,不仅弥补了JADE中种群多样性较小,进化方向不稳定,后期易陷入局部最优的缺陷;同时又利用了质心这一物理学中的概念,能够快速收敛到最优值附近.由此可见,本文方法不仅增加了种群多样性,而且加快了收敛速度与收敛精度,使得算法整体性能得到提高.
3.3 改进的自适应差分进化算法
在差分进化算法中,基于质心的xwbest的选择不仅增加了种群的多样性,而且提高了收敛速度和精度.自适应控制参数的引入,能够动态调整算法中的各个参数,减少人为设置参数的影响.CADE伪代码如算法1:
1)第2-5行,利用差分进化算法初始化种群;设置均值μF和μCR初始值为0.5,p为选择精英种群的概率,c为常量;初始化集合SF和SCR为空集,分别用来存放变异及交叉成功的后代个体所对应的自适应的缩放因子和交叉概率.
2)第7行,自适应缩放因子Fi和交叉概率CRi分别由柯西分布和标准正态分布决定.与正态分布方式不同的是,通过柯西分布产生的缩放因子Fi不仅保证了Fi取值的多样性,而且有效避免了当缩放因子集中于某一具体值时,使用贪心算法进行变异(如DE/best,DE/current-to-best)所产生的过早收敛的现象.
3)第8行,按照本文所提的方法选择出用来变异操作的个体xwbest,加快种群收敛速度及收敛精度.
4)第11行,变异变量Vit由改进后的变异算子确定;由本文方法得到的后代个体不仅保证了种群的多样性而且能够快速向最优值方向进化,加快了种群的收敛速度.
算法1.
Line# Procedure of CADE
01 Begin
02 SetμCR=0.5;μF=0.5;p=0.05;c=0.1;
03 Initial populationxi(0)|i=1,2,…,NP;
04 For t= 1 to T
05SCR=∅;SF=∅;
06 For i = 1 to NP
07 GenerateCRi=randni(μCR,0.1),
Fi=randci(μF,0.1);
08 ChooseXwbestby formulate(9);
09 Randomly choosexr1(t)≠xi(t)from
current populationP;
10 Randomly choosexr2(t)≠xi(t) and
xr1(t)≠xr2(t)from current populationP;
11Vi(t)=xi(t)+Fi(xwbest(t)-xi(t))+Fi(xr1(t)-xr2(t));
12 Generatejrand=randint(1,D);
13 For j = 1 to D
14 Ifj=jrandorrand(0,1) 15ui,j(t)=Vi,j(t); 16 Elseui,j(t)=xi,j(t); 17 End For 18 Iff(xi(t))≤f(ui(t)) 19xi(t+1)=ui(t);CRi→SCR;Fi→SF; 20 Elsexi(t+1)=xi(t); 21 End for 22μCR=(1-c)·μCR+c·meanA(SCR); 23μF=(1-c)·μF+c·meanL(SF) 24t=t+1; 25 End 5)第18-20行,属于差分进化算法的选择阶段,此阶段根据贪婪算法,在当前个体xi(t)和经过交叉后的个体ui(t)之间选择出适应度值更好的个体,并保留到下一代种群中;若中间个体ui(t)优于xi(t),将中间个体保留到下一代;同时,把自适应的缩放因子Fi和交差概率CRi分别存入相应的集合SF和SCR中.在进化过程中,设置合理的控制参数更趋向于产生生存能力较强的后代个体,此时我们就需要将本次变异与交叉的概率记录下来,为下一次的种群进化作为参考. 6)第22-23行,利用表达式μCR=1-c·μCR+c·meanASCR和μF=1-c·μF+c·meanLSF分别对每代的μCR和μF进行更新;meanASCR为算术平均值,meanLSF为Lehmer平均值,其meanL(SF)=∑F∈SFF2/∑F∈SFF.通过对使用Lehmer平均值与算术平均值获得的自适应的μF进行对比,前者对变异成功的缩放因子赋予更大的权重,所得的缩放因子更接近最佳缩放因子;而通过算术平均值获得的缩放因子往往比最佳缩放因子要小,将会使得μF过小进而导致种群过早收敛.因此Lehmer平均值更有利于保留影响较大的缩放因子,进而提高种群的变异概率. 多路径覆盖测试数据生成问题数学模型的建立与路径的表示方法密切相关,且被测程序一般有多条路径.在结构化程序设计中,程序通常由顺序、选择和循环三种结构组成.其中,选择和循环结构决定程序不同分支的走向;对于循环结构,通过引入Z 路径覆盖[16]可将其分解成多个选择结构.现有的路径表示方式有:采用程序的语句编号序列表示路径、采用分支节点序列表示路径和利用赫夫曼编码表示目标路径等方式.本文借鉴GONG等人[17]的基于路径相关性的回归测试数据进化生成论文中的相关路径表示方法,对待测程序进行标记. 假设,待测程序为P,对程序中各个分支节点进行插桩,并设置穿越相应分支节点并且值为真记为1,若为假记为-1,不经过该分支节点则记为0.因此可以通过1,-1和0的编码序列表示程序执行的路径.利用一组输入数据运行插桩后的测试程序,得到分支节点序列为d1,d2,…,dm的执行路径pti,其中,m为路径pti的长度;此外,待测程序P的目标路径为p1,…,pn,n为目标路径条数. 假设程序P的输入域为D,输入数据t1,…,tn∈D.将执行路径pti的编码序列与目标路径pi的编码序列自左向右进行比较,找到二者编码第一次不相同的编码位置,并记录之前相同编码的个数,记为pti∩pj,取其与目标路径编码即目标路径总长度的比值,得到路径相似度,记为fit: (10) 因此,可以把求解测试数据生成问题转化为求取f1(t),f2(t),…,fn(t)的最大值问题,则其适应度函数如下: max(f1(t),f2(t),…fn(t))s.t.t∈D (11) 应用CADE算法自动生成测试数据的模型如图1所示.测试环境的构造是测试数据生成的基础,在该阶段我们对源程序进行静态分析,利用分支函数插桩得到的带编码的测试程序流程图生成目标路径,此方法比传统的数据流程图更加简洁;利用CADE算法生成测试数据是整个模型的核心部分,该阶段根据测试环境构造所得的目标路径及测试数据范围,结合算法所需参数的设置,对种群进行初始化,通过运行改进后的变异算子更新种群,引导种群向最优值方向进化;并利用测试数据运行插桩后的待测程序,计算适应度值. 图1 基于CADE算法的测试数据生成模型Fig.1 Model of test data generation based on the CADE 为评价本文所提出的CADE算法生成测试数据的性能,选择2个基准程序作为被测程序进行实验.针对被测程序,本文主要考察各方法生成测试数据所需的时间,进化代数等,并做出对比实验,清楚地表现出各方法之间的差异.所有实验程序均采用Java语言编写,并在Eclipse下运行,微机环境为Windows操作系统 Intel(R) Core(TM) i3 CPU 2.0GHz和2GB RAM内存.所有试验参数设置如下:种群迭代次数1000,GA交叉概率0.6,GA变异概率0.01,GA算法中的适应度函数来源于文献[18].另外,为降低实验中随机因素的影响,针对不同程序的每一种情况都独立运行50次实验. 三个数排序程序[18]有三个输入变量,有3个判断分支,得到目标路径长度为3;理论路径为8条,其中,不可行路径有1条.为测试CADE算法的性能,本文分别在不同的搜索范围及种群规模下进行对比试验.相关实验结果如表1-表3所示: 表1 种群规模为30,算法运行结果比较 数据范围平均迭代次数平均进化时间GAJADECADEGAJADECADE[0,128]2117120.2790.0370.039[0,512]5425190.6090.1190.103[0,1024]10950292.8140.10.102 从表1-表3中能看出:1)在种群规模相同的情况下,对于同一输入数据范围,CADE算法的迭代次数明显小于GA和JADE,即CADE算法收敛性能高于JADE和GA;2)在种群规模相同的情况下,随着输入数据范围的增加,GA与JADE算法迭代次数相差较大,而CADE算法迭代次数相差不大,说明本文方法的性能要优于GA与JADE算法;3)随着输入范围的增加,CADE算法与遗传算法的时间差不断增大,说明CADE在较大的输入范围内搜索能力强;而相对GA而言,CADE与JADE算法所需平均进化时间相差不大,且CADE平均迭代次数低于JADE算法.总体而言,CADE算法在平均迭代次数及进化时间上更优. 表2 种群规模为50,算法运行结果比较 数据范围平均迭代次数平均进化时间GAJADECADEGAJADECADE[0,128]1614100.2750.0410.043[0,512]3523190.5470.0490.043[0,1024]6132230.8490.050.05 表3 种群规模为100,算法运行结果比较 数据范围平均迭代次数平均进化时间GAJADECADEGAJADECADE[0,128]91080.2950.0510.048[0,512]2017140.4360.070.061[0,1024]3228170.8180.0730.064 本文所选的三角形判断程序[17]共有6个判断分支,得到目标路径长度为6;理论路径为28条,其中,不可行路径有9条,所以实际的目标路径为19条,其中等边三角形的测试数据最难生成. 图2和图3为不同输入范围下,四种方法找到最优解所需的平均迭代次数;其中,[0,64]表示输入数据的取值范围.图2表示种群规模为50,不同输入数据范围下各个方法的平均进化代数;图3种群规模为100,不同输入数据范围下各个方法的平均进化代数.从图2和图3中可以看到CADE算法的总体性能优于其他三种算法,而且随着数据输入范围的增大,CADE能够保证在一定进化代数内找到所需测试数据,性能趋于稳定. 图4和图5表示四种算法在种群规模为50的情况下的平均进化代数与分支覆盖率间的关系;其中,图4的数据输入范围为 [0,1024],图5的数据输入范围为[0,64].从图4和图5中可知,在迭代初期四种算法的覆盖率相差不大,随着平均进化代数的增加,CADE很快达到100%的覆盖率;针对不同的输入范围,在满足分支覆盖率为100 %时,CADE算法平均进化代数明显小于GA、DE和JADE算法,表明本文方法的性能优于GA、DE和JADE算法. 本文在研究测试数据生成问题时,首次将自适应差分进化算法应用于解决测试数据生成问题.本文在已有的自适应差分进化算法JADE基础上,借助自动调节缩放因子的方式,丰富种群的多样性,防止算法陷入局部最优;同时,采用基于质心原理的策略来选择用于变异的个体,能够快速收敛到最优值附近,引导算法向最优值方向进化,使得算法整体性能得到提高.最后,通过仿真试验,表明了本文所提出的算法较好地解决了传统遗传算法在搜索最优解时易陷入局部最优及搜索精度低等缺陷,且能够快速生成所需数据. 图2 不同数据范围,算法平均进化代数Fig.2 Different data range,the algorithm′s average number of iterations 图3 不同数据范围,算法平均进化代数Fig.3 Different data range,the algorithm′s average number of iterations 图4 进化代数与分支覆盖率的关系Fig.4 Relationship between the number of iterations and the rate of branch coverage 图5 进化代数和分支覆盖率的关系Fig.5 Relationship between the number of iterations and the rate of branch coverage [1] Qiu Xiao-kang,Lin Xuan-dong.A path-orientedtoolsupporting fortesting [J].Acta Electronica Sinica,2004,32(12A):231-234. [2] Deb K,Pratap A,Agarwal S,et al.A fast and elitist multiobjective genetic algorithm:NSGA-II [J].IEEE Transactions on Evolutionary Computation,2002,6(2):182-197. [3] Koleejan C,Xue B,Zhang M.Code coverage optimization in genetic algorithms and particle swarm optimization for automatic software test data generation[C].2015 IEEE Congress on Evolutionary Computation (CEC),IEEE,2015:1204-1211. [4] Zhou Y,Li X,Gao L.A differential evolution algorithm with intersect mutation operator [J].Applied Soft Computing,2013,13(1):390-401. [5] Hui S,Suganthan P N.Ensemble and arithmetic recombination-based speciation differential evolution for multimodal optimization [J].IEEE Transactions on Cybernetics,2016,46(1):64-74. [6] Storn R,Price K.Differential evolution-a simple and efficient heuristic for global optimization over continuous spaces [J].Journal of Global Optimization,1997,11(4):341-359. [7] Becerra R L,Coello C A C.Cultured differential evolution for constrained optimization [J].Computer Methods in Applied Mechanics and Engineering,2006,195(33):4303-4322. [8] Gong W,Cai Z.An improved multi-objective differential evolution based on Pareto-adaptive-dominance and orthogonal design [J].European Journal of Operational Research,2009,198(2):576-601. [9] Liao T W.Two hybrid differential evolution algorithms for engineering design optimization [J].Applied Soft Computing,2010,10(4):1188-1199. [10] Zhang J,Sanderson A C.JADE:adaptive differential evolution with optional external archive [J].IEEE Transactions on Evolutionary Computation,2009,13(5):945-958. [11] Gong W,Cai Z,Ling C X,et al.Enhanced differential evolution with adaptive strategies for numerical optimization[J].IEEE Transactions on Systems,Man,and Cybernetics,Part B (Cybernetics),2011,41(2):397-413. [12] Yang Z,Tang K,Yao X.Self-adaptive differential evolution with neighborhood search[C].2008 IEEE Congress on Evolutionary Computation (IEEE World Congress on Computational Intelligence),IEEE,2008:1110-1116. [13] Yi W,Zhou Y,Gao L,et al.An improved adaptive differential evolution algorithm for continuous optimization [J].Expert Systems with Applications,2016,44:1-12. [14] Epitropakis M G,Tasoulis D K,Pavlidis N G,et al.Enhancing differential evolution utilizing proximity-based mutation operators[J].IEEE Transactions on Evolutionary Computation,2011,15(1):99-119. [15] Das S,Konar A,Chakraborty U K.Annealed differential evolution[C].2007 IEEE Congress on Evolutionary Computation.IEEE,2007:1926-1933. [16] Xia Hui,Song Xin,Wang Li.Research of test case auto generating based on Z-path coverage [J].Modern Electronics Technique,2006,29(6):92-94. [17] Wu Chuan,Gong Dun-wei.Evolutionary generation of test data for regression testing based on path correlation [J].Chinese Journal of Computers,2015,38(11):2247-2261. [18] Ding Rui,Dong Hong-bin,Zhang Yan,et al.Fast automatic generation method for software testing data based on key-point path [J].Journal of Software,2016,27(4):814-827. 附中文参考文献: [1] 邱晓康,李宣东.一个面向路径的软件测试辅助工具[J].电子学报,2004,32(12A):231-234. [16] 夏 辉,宋 昕,王 理.基于 Z 路径覆盖的测试用例自动生成技术研究[J].现代电子技术,2006,29(6):92-94. [17] 吴 川,巩敦卫.基于路径相关性的回归测试数据进化生成[J].计算机学报,2015,38(11):2247-2261. [18] 丁 蕊,董红斌,张 岩,等.基于关键点路径的快速测试用例自动生成方法[J].软件学报,2016,27(4):814-827.4 CADE算法应用于测试数据的生成
4.1 适应度函数的构造
4.2 测试数据生成模型
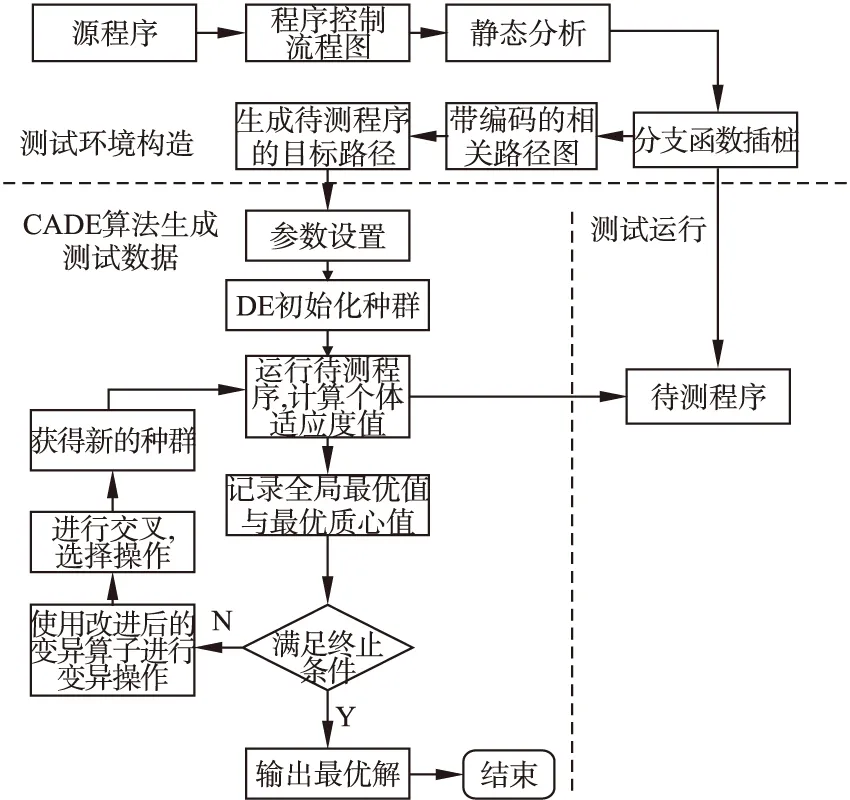
5 实验分析
5.1 三个数排序
Table 1 NP=30,Comparison of experimental results
Table 2 NP=50,Comparison of experimental results
Table 3 NP=100,Comparison of experimental results
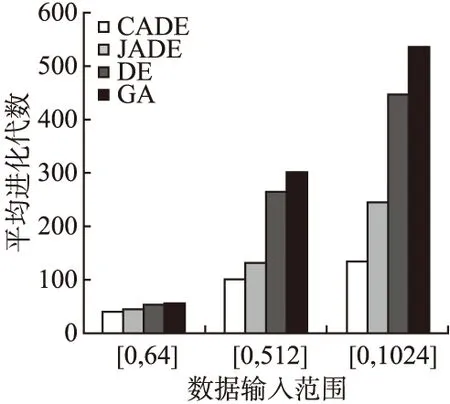
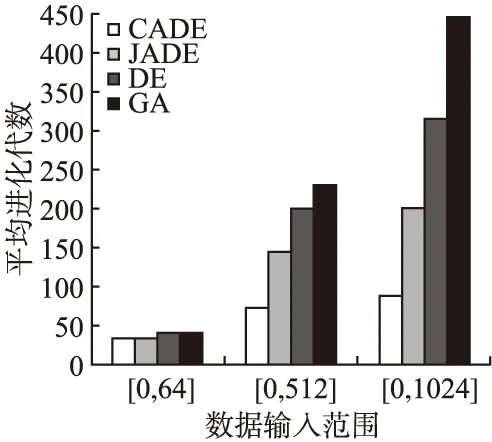
5.2 三角形判断
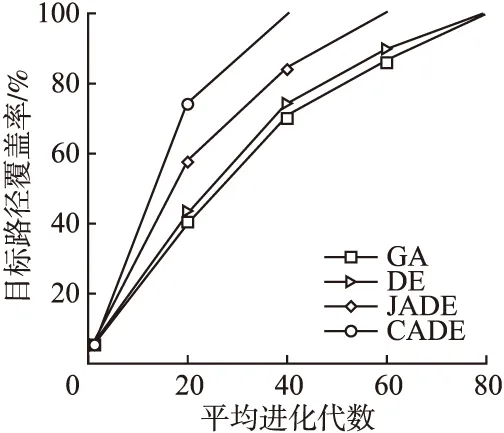
6 结 论