基于朴素贝叶斯的信任决策模型

2018-03-27 01:27沈宏伟张阳洋刘宗田

小型微型计算机系统 2018年2期

沈宏伟,邵堃,张阳洋,霍星,刘宗田

1(合肥工业大学计算机与信息学院,合肥 230009) 2(合肥工业大学数学学院,合肥 230009) 3(上海大学计算机工程与科学学院,上海 200072) 4(南瑞集团国电南瑞科技股份有限公司,南京 211106)

1 引言

信任关系是一种在人类社会中普遍存在的人际关系,这种关系表现在日常生活中的各个方面.随着互联网技术的发展及其应用的普及,日常生活中的交互活动逐渐向网络生活中转移,比如网购、微博、微信等.由于网络环境具有动态性、匿名性、开放性的特点,日常生活中对信任的评估方法已经不能充分适应当前复杂的网络环境.

因此,适用于网络环境下的信任评估方法作为衡量网络实体行为可靠性的有效方法,得到越来越多的学者们关注.Blaze[1]为解决internet上网络服务的安全问题,首先提出了“信任管理”的概念.至今,信任管理总体上仍处于发展初期.但是,国内外学者对信任模型的研究一直不断取得突出成果[2-8].学者们对信任模型的研究主要分为两大类:一类是基于概率理论的信任模型[2-5];一类是基于模糊理论的信任模型[6-8].

信任是来源于信任主体所拥有的经验,主体对客体某种特定行为的预期,会随着客体的行为而发生变化.jsang[9]等人基于主观逻辑信任,通过引入事实空间和观念空间的概念来描述和度量信任关系.唐文[10]等人针对信任的模糊性提出了一种基于模糊逻辑的主观信任计算方法.文献[11]对开放式系统中的动态信任预测模型进一步优化,提出了一种符合人类心理认知过程的信任预测模型,摒弃了已有的文献中常用的确定权重来进行预测的主观方法,同时提出了在直接信任不存在情况下解决信任计算的办法.文献[12]提出了一种正态分布下的动态推荐信任模型,通过计算间接信任影响因素,运用分级剪枝方法过滤推荐信息,计算得到后验分布期望的贝叶斯估计.文献[13]提出了一个基于服务Agent的可信性评估方法,从社交认知角度建立的服务Agent信任本体,提出一系列的信任推理的计算规则来支持信任值的计算.

在对以上研究成果的分析研究过程中发现,现有的信任研究都专注于对信任度值量化分析,忽略了信任度对决策的指导性作用,并且在计算信任度时,学者们普遍使用直接信任和间接信任忽略了信誉的重要作用.文献[14]指出了直接信任、间接信任、信誉之间的相互作用关系,认为信誉和直接信任之间存在一定的修正关系,可以避免直接信任的误导.如果当直接信任、间接信任以及信誉出现差异时,主体很难通过其中一种信任关系来对客体进行客观行为进行决策.而且,信任关系是一种不确定关系,兼具主观性和模糊性.因此,本文通过深入研究信任关系中直接信任、间接信任、信誉的联系,将朴素贝叶斯算法和模糊理论相结合建立信任决策模型,能够更加准确可靠的帮助主体进行信任决策.

2 信任特征属性量化

2.1 直接信任度量化

定义1.直接信任度(Direct Trust,DT)是依据信任主体i根据与信任客体j的历史交互经验得到的信任客体的可信度.

直接信任来自信任的主客体之间频繁的历史交互,是信任主体对信任客体的主观判断,受到多个方面因素的影响,包括信任主体的心理因素,历史交互数量及时间因素,交互的顺利程度等,这些因素都会影响信任主客体之间的直接信任度.由于主体的心理和交互的顺利程度无法进行获取,因此本文借助历史交互数量及时间因素来对直接信任建立数学模型,如公式(1)所示:

(1)

2.2 间接信任度量化

定义2.间接信任度(Indirect Trust,IDT)是信任主体(i)借助与信任客体(j)有过交互经验的第三方推荐所获得的信任度.若有第三方推荐者p向信任主体推荐信任客体,则推荐信任度可用公式(2)表示:

(2)

(3)

2.3 信誉量化

定义3.信誉(Reputation,RE),也称声誉是信任客体为获得信任主体的认可,通过大量交互来获得信任主体对其的客观评判.信誉是全部信任主体对信任客体信任度的加权平均.因此,信誉可以表示为:

(4)

3 朴素贝叶斯信任决策模型

3.1 朴素贝叶斯分类算法

贝叶斯算法由英国数学家Thomas Bayes提出,并成为概率论的基础理论,主要应用于决策理论、统计推断、统计的估算等领域.朴素贝叶斯(Native Bayesian,NB)是贝叶斯的一种特例,是贝叶斯证据独立的表达形象.朴素贝叶斯与一般贝叶斯的主要区别在于,朴素贝叶斯要求各个特征属性(characteristic attribute,CA)相互独立.满足独立条件的朴素贝叶斯分类算法比一般贝叶斯算法速度更快,更简单,分类准确率更高.

朴素贝叶斯分类算法应用在本文信任模型需满足两个基本假设:

假设1.交互成功的事件要比交互失败的事件平均具有更高的直接信任度、间接信任度以及信誉值.

假设2.直接信任、间接信任和信誉在交互结果给定的情况下是独立的.

假设1,显然很容易满足.假设2,由于间接信任通过直接信任计算而来,两者看似不独立.但是两者来自不同信任主体,间接信任计算所采用的是推荐者与信任客体之间的直接信任,此直接信任和信任主体与信任客体之间的直接信任是相互独立的,所以假设2也可满足.

3.2 朴素贝叶斯信任决策模型

直接信任,间接信任,信誉作为信任交互结果的三个特征属性,而且很好的满足了朴素贝叶斯的特征条件相互独立的基本假设.建立朴素贝叶斯信任决策模型,首先需要对训练样本进行统计和计算,包括交互成功和失败的样本数目,以及交互结果所对应的三个特征属性,直接信任,间接信任以及信誉的分布.

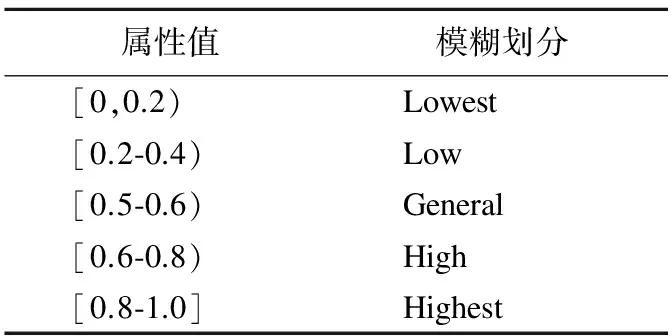
由于直接信任,间接信任和信誉的值所在区间是[0,1],不能够体现出人对其评价的主观模糊性.人在对事物进行评价的时候往往只是“好”、“坏”之分,而不是有一个精确的度量.但是,完全采用这种二值逻辑无法完全胜任这种模糊表达的能力,而且缺乏灵活性.据此对其做一个模糊划分,如下页表1所示.本文将属性值划分为5个区间:{ Lowest,Low,General,High,Highest }.这样不仅符合模糊评价的质量要求,而且有一个中间等级符合自然语言描述.

依据表1中的划分,直接信任DT={Lowest,Low,General,High,Highest},间接信任IDT={Lowest,Low,General,High,Highest},信誉RE={Lowest,Low,General,High,Highest}.

定义4.交互结果(Interaction Result,IAR),是信任主体与信任客体直接发生交互,对此次交互成功与失败的评判,其中IAR={Success,Fail}.将交互结果分为成功和失败两大类,是本文模型进行决策的最终依据.

表1 属性值模糊划分
Table 1 Attribute values fuzzy divided

属性值模糊划分[0，0．2)Lowest[0．2⁃0．4)Low[0．5⁃0．6)General[0．6⁃0．8)High[0．8⁃1．0]Highest

通过以下式子计算各个类别下各个特征属性的条件概率估计,即P(CA|IAR).首先将训练样本集根据交互结果IAR={Success,Fail}进行分类.然后根据直接信任度,间接信任度,信誉值的划分进行统计,获得在不同交互结果下的先验条件概率分布.

具体步骤如下:

1)输入训练样本数据;

2)计算样本数据中,信任主客体的直接信任、间接信任、信誉;

3)根据计算结果对交互结果及其直接信任、间接信任、信誉所属划分进行计数;

4)重复1),2),3)步,直至训练样本数据处理完毕.

根据以上步骤操作可以获得交互成功、交互失败的交互数量,及各个交互所对应的直接信任、间接信任、信誉所属划分的数量.特征属性统计数量如表2所示.

表2 交互结果及其特征属性统计数量表
Table 2 Interaction result and characteristic attributes statistical table

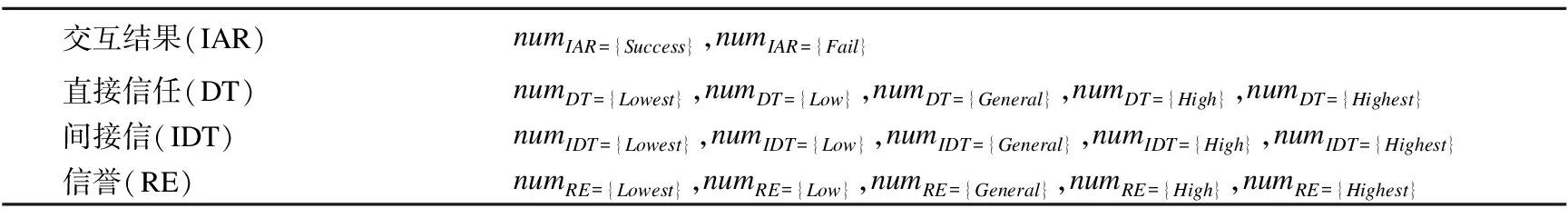
交互结果(IAR)numIAR={Success}，numIAR={Fail}直接信任(DT)numDT={Lowest}，numDT={Low}，numDT={General}，numDT={High}，numDT={Highest}间接信(IDT)numIDT={Lowest}，numIDT={Low}，numIDT={General}，numIDT={High}，numIDT={Highest}信誉(RE)numRE={Lowest}，numRE={Low}，numRE={General}，numRE={High}，numRE={Highest}

由于各个特征属性相互独立,则可根据贝叶斯定理得到公式(5):

(5)

由于P(CA)对于各个类别都是相同的,可看作常数.因此,分子主要观察对象.由于各个特征属性之间相互独立,因此分子部分等价于联合分布模型.则反复使用链式法则将其改写为条件概率形式,如公式(6):

P(IAR|CA)

=P(IAR|DT,IDT,RE)

=P(IAR)P(DT,IDT,RE|IAR)

=P(IAR)P(DT|IAR)P(IDT,RE|IAR,DT)

=P(IAR)P(DT|IAR)P(IDT|IAR,DT)P(RE|IAR,DT,IDT)

=P(IAR)P(DT|IAR)P(IDT|IAR)P(RE|IAR)

(6)

由式(6)知,交互结果的后验概率通过交互结果的先验概率及信任特征属性的先验概率计算获得.因此,获取先验概率是朴素贝叶斯信任决策模型的重点.通过对训练样本集的统计训练,获得各个特征属性的先验概率是进行判别计算的关键.在得到三维特征属性的先验概率之后,便可对未知交互结果的交互事件进行预测并提供相关的决策信息.对于已知直接信任DT,间接信任IDT,信誉RE的交互事件X,交互事件X的交互结果未知.则可通过比较P(CA|Success)P(Success)和P(CA|Fail)P(Fail)的值,预测此次交互X的交互结果.

4 实验及分析

实验数据集来自EPINIONS dataset,本文选用EPINIONS dataset是由于此数据集在研究社会网络信任关系领域被许多学者所采用.EPINIONS dataset中包含49290位用户对139738个对象进行了评价,并且评价次数不低于1次,一共发表了664824次评论,一共拥有487181对相互信任的用户.

首先对获取的664824次评论进行统计,根据评论来将此次交互结果(IAR)分为成功(Success)和失败(Fail)两类.数据集中评论分为1-5,5个等级,实验过程中规定1-3为较低的评价,即交互失败,4-5为较高评价,即交互成功,见表3.

表3 交互结果统计
Table 3 Statistical interaction results

交互结果(IAR)成功(Success)失败(Fail)统计数量495393169431

接下来对交互结果的三个属性特征直接信任,间接信任,信誉进行统计,统计结果如下页表4所示.

实验过程中,直接信任度是信任主体对信任对象的直接评价,与直接信任所属划分相对应.亲密度的计算是根据信任主体与推荐者所交互对象共同数量确定的.

建立朴素贝叶斯模型的关键在于计算每一个特征属性的条件概率分布,借助条件概率分布实现各个特征属性的融合.条件概率分布为朴素贝叶斯模型提供了不确定性计算所必需的先验概率,进而可以求出交互结果的后验概率.朴素贝叶斯模型各个特征属性的条件概率估计如下页表5-表7.

以上是对训练样本中交互结果及其特征属性的统计,并计算各个特征属性的条件概率估计.下面对1000组测试样进行测试,已知直接信任DT,间接信任IDT,信誉RE的交互X={x1,x2,x3,…,x1000},交互X的交互结果已知,其中交互结果成功有628个,失败372个.根据训练样本计算获得的预测交互结果与已知交互结果进行比较获得模型的准确度.

表4 交互结果特征统计表
Table 4 Statistical feature attribute of interaction results

LowestLowGeneralHighHighest成功Success直接信任(DT)175152468443897169731239566间接信任(IDT)456121216094137386340246信誉(RE)85386616823143702333149失败Fail直接信任(DT)2615428698416323956033387间接信任(IDT)422615176466996879434536信誉(RE)422615465489417040930390

表5 直接信任条件概率估计
Table 5 Direct trust conditional probability

表6 间接信任条件概率估计
Table 6 Indirect trust conditional probability

表7 信誉条件概率估计
Table 7 Reputation conditional probability

具体步骤如下:

1)根据公式(1)(2)(3)(4)(5),计算获得直接信任,间接信任以及信誉的值.

2)利用表1,对直接信任度,间接信任度,信誉值进行划分.

3)借助表5-表7,使用以下公式分别计算交互成功和交互失败的后验概率如公式(7)(8):

(7)

(8)

其中

(9)

evidence是用来控制交互成功和交互失败的后验概率之和为1.

4)比较交互成功的后验概率和交互失败的后验概率获得交互的预测结果,与已知结果进行比较,并记录.

5)反复执行1),2),3),4)步,直到全部测试样本测试完毕.

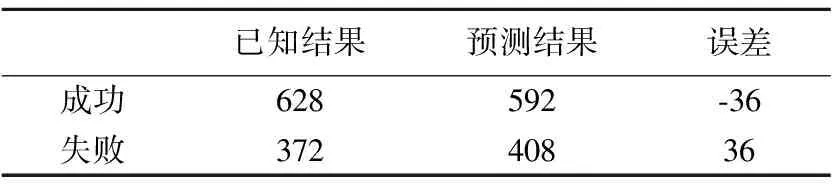
表8 对比结果
Table 8 Comparison result

已知结果预测结果误差成功628592⁃36失败37240836

根据以上步骤对测试样本进行测试,测试结果如表8、下页表9所示.

表8中看出,测试样本中,交互成功的数量为628,交互失败的数量为372,使用模型进行预测的结果是交互结果成功的数量为592,交互失败的数量为408.

表9 交互结果转移表
Table 9 Interaction results transfer table

成功(已知)→失败(预测)失败(已知)→成功(预测)5519

根据表9可以看到,在测试样本中原来有55个交互成功的样本经过模型计算后预测结果是失败,19个在测试样本中交互结果是失败的经过模型计算后预测结果是成功,即一共有74个样本预测结果与已知结果不匹配.可粗略估计本模型的准确率在92.6%,这是一个可以让人接受的准确率.

表10 恶意评论
Table 10 Malicious bad review %

间接信任LowestLowGeneralHighHighest成功后验概率9．87187．499025．914966．964490．9089失败后验概率90．128292．501074．085133．03569．0911交互结果预测失败失败失败成功成功

模型不仅具有较高的准确率,而且对恶意差评和过分好评也有着一定的抵御能力.恶意评论是指对交互对象给予过低的评价.而过分好评相反,指的是给予交互对象一个过高的评价,这直接影响到间接信任.以一次交互为例,直接信任和信誉均处于较高评分,即IDT、RE={High},交互成功和交互失败的后验概率如表10所示.

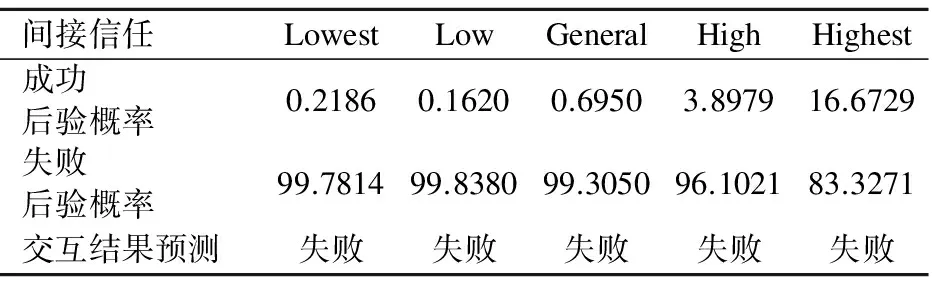
表11 过分好评
Table 11 Extremely high praise %

间接信任LowestLowGeneralHighHighest成功后验概率0．21860．16200．69503．897916．6729失败后验概率99．781499．838099．305096．102183．3271交互结果预测失败失败失败失败失败

由表10可以看出,在直接信任DT=High,信誉RE=High时,间接信任IDT={Lowest,Low,General}则预测交互结果为失败;间接信任IDT={High,Highest}则预测交互结果为成功.即如果初始的间接信任为Highest时,恶意评论对其影响不是很大,需要恶意评论影响间接信任度致其低于0.6方可影响到对交互结果的判断.假设所有推荐者与信任主体亲密度相等,初始推荐者有20人,融合间接信任度为0.9={Highest},现有n个恶意差评者,其信任主体对其间接信任度为0.1,则需要n>12个恶意推荐者才能影响模型对交互结果的预测.同理可知,模型对过分好评也有一定的抵御作用.如表11所示,其中直接信任DT={Low},信誉RE={Lowest}.当直接信任与信誉比较低的时候,过分好评对其的影响微乎其微,并没有影响到对决策结果的判断.因此,本文模型对恶意推荐也有着一定的抵御作用.

5 结束语

信任模型的构建一直是信任研究领域的重点.本文利用朴素贝叶斯理论,用直接信任,间接信任,信誉作为三维特征属性描述交互结果.其中也涉及到了直接信任,间接信任以及信誉的计算问题,借助模糊理论方法将三者根据值所属范围进行划分,然后计算信任的三维特征属性的先验条件概率估计.根据先验概率估计来计算交互结果的后验概率估计,构建信任决策模型.该模型将根据交互情况计算交互的三维特征属性,并结合三维属性特征划分和交互结果的后验概率预测此次交互的结果,完成决策分析功能.本文模型不仅具有较高的准确度,而且对恶意评论和过分好评也有一定抵御作用.

[1] Blaze M,Feigenbaum J,Lacy J.Decentralized trust m anagement[C].IEEE Computer Society,1996:164-173.

[2] Abdul-Rahman A,Hailes S.A distributed trust model[C].The Workshop on New Security Paradigms,ACM,1998:48-60.

[3] Tan Zhen-hua,Wang Xing-wei,Cheng Wei,et al.A distributed trust model for peer-to-peer networks based on multi-dimension-history vector[J].Chinese Journal of Computers,2010,33(9):1725-1735.

[4] Angin P,Zhong Y,Lu Y,et al.A computational dynamic trust model for user authorization[J].IEEE Transactions on Dependable & Secure Computing,2015,12(1):1-15.

[5] Hoogendoorn M,Jaffry S W,Van Maanen P P,et al.Design and validation of a relative trust model[J].Knowledge-Based Systems,2014,57(to appear):81-94.

[6] Sentz K.Combination of evidence in dempster-shafer theory[D].Binghamton,NY:Systems Science and Industrial Engineering Department,Binghamton University,2002.

[7] Tajeddine A,Kayssi A,Chehab A,et al.Fuzzy reputation-based trust model[J].Applied Soft Computing,2011,11(1):345-355.

[8] Wang Ying,Wang Xin,Zuo Wan-li.Trust prediction modeling based on social theories[J].Journal of Software,2014,25(12):2893-2904.

[10] Tang Wen,Hu Jian-bin,Chen Zhong.Research on a fuzzy logic-based subjective trust management model[J].Journal of Computer Research and Development,2005,42(10):1654-1659.

[11] Li Xiao-yong,Gui Xiao-lin.Cognitive model of dynamic trust forecasting[J].Journal of Software,2010,21(1):163-176.

[12] Shao Kun,Luo Fei,Mei Xiao-xiong,et al.Normal distribution based dynamical recommendation trust model[J].Journal of Software,2012,23(12):3130-3148.

[13] Zhu Man-ling,Jin Zhi.Approach for evaluating the trust worthiness of service agent[J].Journal of Software,2011，22(11):2593-2609.

[14] Kiefhaber R,Jahr R,Msadek N,et al.Ranking of direct trust,confidence,and reputation in an abstract system with unreliable components[C].Ubiquitous Intelligence and Computing,2013 IEEE,International Conference on and,International Conference on Autonomic and Trusted Computing,IEEE,2013:388-395.

附中文参考文献：

[3] 谭振华,王兴伟,程维,等.基于多维历史向量的P2P分布式信任评价模型[J].计算机学报,2010,33(9):1725-1735.

[8] 王英,王鑫,左万利.基于社会学理论的信任关系预测模型[J].软件学报,2014,25(12):2893-2904.

[10] 唐文,胡建斌,陈钟.基于模糊逻辑的主观信任管理模型研究[J].计算机研究与发展,2005,42(10):1654-1659.

[11] 李小勇,桂小林.动态信任预测的认知模型[J].软件学报,2010,21(1):163-176.

[12] 邵堃,罗飞,梅枭雄,等.一种正态分布下的动态推荐信任模型[J].软件学报,2012,23(12):3130-3148.

[13] 朱曼玲,金芝.一种服务Agent的可信性评估方法[J].软件学报,2011,22(11):2593-2609.