一种隐私保护的序列数据马尔可夫分类方案

李宗峰，黄刘生，沈 瑶，许 杨，聂熠文，杨 威

1(中国科学技术大学 计算机科学与技术学院，合肥 230027) 2(中国科学技术大学 苏州研究院，江苏 苏州 215123)

1 引 言

序列数据分为时间序列数据、DNA序列数据、语音数据、自然语言数据等.序列数据分类是目前数据挖掘领域的一个研究热点.本文将主要研究使用马尔可夫模型对序列数据进行分类时的隐私保护.

数据挖掘是在大型数据存储库中，自动地发现有用信息的过程[4].数据挖掘主要有分类、聚类和关联分析等研究方向.分类就是确定对象属于哪个预定义的目标类[4].分类任务一般分为两步，第一步根据输入数据建立分类模型，第二步利用分类模型对待分类数据进行分类.常见的分类模型主要有决策树模型、神经网络模型、基于规则的模型、支持向量机模型、贝叶斯模型等.

序列分类是分类算法的一个类别，其输入是序列数据，输出是对这个序列的某个离散标记.针对序列数据，常见的分类方案有如下几种：一是借助于序列数据的领域知识或者特点进行分类，这种方法存在通用性差、特点难以发现等特点；二是使用传统的特征分类算法进行分类，使用这种方法需要找到有效的特征查找方法，但很多序列数据难以找到有效的特征；第三种是使用概率模型对数据进行分类，该方案在序列数据分类中比较常见，针对序列数据，有较完善的数学基础；同时具有效率与准确性较高，通用性强的优势.

马尔可夫模型是一个描述随机过程的概率模型.作为一种分类方法，马尔科夫模型的准确度和参与训练的具有代表性的数据量密切相关.因此如何获得足够多的具有代表性的数据成为一个关键问题.

某机构或个人获得的序列数据往往是相同类型，会导致数据的代表性比较差，无法训练出有效的模型.此时比较好的方案是与多个机构合作进行训练，这就可以获得足够多有代表性的数据，所以多个机构或个人合作训练模型是一种解决问题的有效办法.

多个机构或个人合作训练模型能够获得比较好的模型，但并不是所有的机构或个人都同意直接共享数据.例如某机构持有购买的金融市场的金融产品价格数据或持有某些具有基因缺陷的人类基因信息.如果直接共享数据，会造成这些机构或个人在法律或者隐私等方面的担忧，例如遗传病的基因标记[3].这种情况下，如何保证每个合作的机构或个人的数据隐私是一个非常重要的考虑.

基于上述实际场景的需求，本文主要介绍了在多方参与者拥有序列数据并且保护各方隐私的情况下，共同训练马尔科夫模型的方案.本文提出的方案不仅可以训练出传统的一阶马尔可夫模型，还可以训练k阶马尔可夫模型，k阶马尔可夫模型可以提高模型的分类准确度[5].此方案还能够对随着时间变化的数据做到有效的处理，此外，此方案的各项开销(计算、通信等开销)比[2]中介绍的同态加密方案低，是一种高效可行的方案.

2 预备知识

本文主要针对马尔可夫模型的隐私保护进行讨论.在这一节将首先对马尔可夫模型进行简要概述，接着对隐私保护方法进行简要说明.本文采用的方案与目前已有的同态加密方案[2]相比，具有简单、高效以及能够更好的处理随时间变化的数据等特点.

2.1 马尔可夫模型

马尔可夫模型是一种广泛使用的统计模型，目前已经成功应用在语音识别、输入法等领域.

马尔可夫链分为连续时间马尔可夫链与离散时间马尔可夫链，本文中使用的马尔可夫模型为离散时间马尔可夫链.下面分别介绍一阶与K阶马尔可夫模型.

马尔科夫链是一系列状态的集合，集合中每一个状态发生的概率只与前一个状态有关，与集合中其他状态无关.这里为方便表示，将状态集合表示为∑.例如，如果用S表示一个长度为n的序列，这个序列的第i个状态表示为Si，这个状态的值表示为si.这样第i个状态发生的概率可以如下表示

P(Si=si|Si-1=si-1,Si-2=si-2，…S1=s1)

=P(Si=si|Si-1=si-1)

即任何一个状态发生的概率只与前一个状态有关，与前面其他状态无关.可以计算出序列S的概率

P(S)=P(Sn=sn|Sn-1=sn-1)P(Sn-1=sn-1|Sn-2=sn-2)…

简化为：

P(S) =P(sn|sn-1)P(sn-1|sn-2)…P(s1)

上式的主要参数为每个状态的先验概率和状态之间的转移概率.对于任意状态Si，其先验概率为：

上式中num(si)表示状态Si出现的次数，∑sj∈∑count(sj)表示所有状态出现的次数总和.

马尔科夫模型对序列数据分类就是首先根据训练数据对每个类计算以下参数：类中每个状态发生的先验概率，类中状态之间的转移概率.经过训练之后每个类都有一个先验概率向量和一个转移概率矩阵.使用马尔科夫模型的方法如下：对于任意一个新的序列数据S，分别使用每个类训练的参数计算S发生的概率，然后将所有计算所得的概率求最大值，概率最大值对应的类就是S的类标.

K阶马尔科夫模型相对于一阶马尔科夫模型，每个状态发生的概率不仅仅与前一个状态有关，而且与紧邻的前k个状态有关，并且也只与前k个状态有关.这种情况下，每种状态的发生概率变为：

P(Si=s|Si-1=si-1,Si-2=si-2,…S1=s1)

=P(Si=si|Si-1=si-1,…,Si-k=si-k)

对于时间序列S其发生的概率为

K阶马尔可夫模型下，任何一个状态的先验概率为：

上式中num(s1,s2,…,sk-1,sk)表示序列s1,s2,…,sk-1,sk在训练数据集中出现的次数，num(所有k长度序列)表示所有长度为k的序列在训练数据集中出现的次数总和.

对于任意状态si与序列s1,s2,…,sk-1,sk的转移概率为：

上式中num(s1,s2,…,sk-1,sk,si)是序列s1,s2,…,sk-1,sk,si出现的次数.num(s1,s2,…,sk-1,sk)是序列s1,s2,…,sk-1,sk出现的次数.

K阶马尔科夫模型与一阶马尔科夫模型类似.首先使用训练数据针对每个类计算出每个状态的先验概率以及状态转移矩阵.对于任意序列S，使用每个类的先验概率和状态转移矩阵计算其发生的概率，概率最大的类标即为序列S的类标.

2.2 隐私保护技术

隐私包括很多方面，例如数据隐私、模型参数隐私等.本文中隐私主要是指数据内容隐私以及数据统计特征的隐私.本文中隐私为每个参与方所持有的数据内容以及统计特征，所有参与方数据总体的统计特征并不是隐私.一直以来隐私保护问题依赖于数据分析方法[1].很多数据挖掘和机器学习算法通过扩展能够做到保护隐私，这类拓展大多分为两类.第一类是对数据加扰动，例如随机化、旋转或多重采样[2，7-9，12，14].这类方法会造成一定的数据损失.第二类是在计算过程中使用密码学方法对数据进行保护[2，10，11，13，15，16].这类方法理论上不会造成数据损失.本文方案属于第二类.本文主要使用了群，哈希函数，幂乘等来实现隐私保护.

目前已经有马尔可夫模型的隐私保护方案，[2]中提出的方案主要借助同态加密技术实现隐私保护，同态加密具有复杂、效率低等特点.本文提出的方案比较简单，效率较高，能够更好的处理随时间变化的数据.

本文提出的方案使用的隐私保护技术主要参考[1]，要点包括可信第三方确定一个群，以及n+1(参与方数目为n)个密钥s0，s1,s2…，sn，其中所有密钥之和为0，其中群是公开的，G是一个p阶循环群，p是素数，g为生成元，G满足decisional Diffie-Hellman(DDH)assumption.每个参与方获得一个密钥，剩下的一个密钥分给最终模型训练者.对于任意参与者i，在t时刻加密其参数x，此时计算

Ci=gxH(t)Ki

其中，H(t)为公开的哈希函数.Ki为参与者i的密钥.每个参与者都计算Ci，并将Ci发送给最终模型训练者，最终模型训练者计算

化简可得

本文的隐私保护主要借助于密码学技术，包括群运算以及哈希函数等.本方案使用的密码学技术已经在[1]中进行了证明.

3 一种基于隐私保护的马尔可夫序列分类方法

本方案为在保护各参与方隐私的前提下合作训练马尔科夫模型.简化起见，假设参与方有A与B，其中A为最终的模型训练者，A与B分别掌握一定数量的序列数据，A与B希望合作训练马尔可夫模型，下面将针对一阶与k阶马尔科夫模型进行说明.

3.1 一阶马尔可夫模型

训练马尔可夫模型的核心为：对每一类序列数据，计算每一个状态的先验概率和状态之间的转移概率.

此处使用C表示训练集合中序列数据所有类的集合，对于第i个类使用ci作为类标.

对任意状态s，其在类ci中的先验概率为

上式中num(s,ci)表示类ci中状态s出现的次数，num(ci)表示类ci中所有状态出现的次数的总和.

当数据分布在A和B两方时，类ci中状态s的先验概率为

上式中，numA(s,ci)表示A的数据上，类ci中状态s出现的次数，numB(s,ci)表示B的数据上，类ci中状态s出现的次数，numA(ci)表示A的数据上，类ci中所有状态出现的次数的总和，numB(ci)表示B的数据上，类ci中所有状态出现的次数的总和.

训练模型，就是计算numA(s,ci)+numB(s,ci)和numA(ci)+numB(ci)的值。此处借鉴了参考文献[1]中一种处理方法。此方法的正确性已经在文献中进行了证明.

除A、B外，还需有一个可信第三方T，T首先生成群G以及三个密钥keyA、keyB、keyC，群G生成元为g，阶为p，keyA+keyB+keyC=0.T分发keyA给A，分发keyB给B，并将训练最终模型的密钥keyC给A.A与B分别在各自本地数据上进行训练，计算每个类中各个状态的先验概率，不同状态之间的转移概率等参数.A、B针对每一个参数计算对应的加密参数，例如A计算的某个参数值为parA，B计算的对应的参数值为parB，则A计算加密参数为basekeyA*gparA，B计算结果为basekeyB*gparB，，其中base为A与B共享的哈希函数H(t):Z→G，t为当前时间.A、B将各自计算所得的结果发给最终模型训练者A，A将各个参与方的计算结果与basekeyC相乘得到V=basekeyC*basekeyA*gparA*basekeyB*gparB=gparA+parB，V与g已知，可计算得到parA+parB.将模型所有参数用上述流程计算可得到最终的模型.算法总结如算法1所示

算法1.隐私保护的一阶马尔可夫序列分类

输入：A有数据集DA，B有数据集DB，T为可信第三方

输出：保护DA与DB隐私前提下A、B每隔PT时刻合作训练马尔可夫模型

1 在时刻t，T向A与B分发密钥以及g等参数.

2 每隔PT时刻(每一轮)：

3 for 每个类cido

4 A在DA上计算类ci中每个状态出现的次数.

5 B在DB上计算类ci中每个状态出现的次数.

6 for每个状态sado：

7 A在DA上计算类ci中sa出现的次数

numA(Sa,ci)

8 B在DB上计算类ci中sa出现的次数

numB(Sa,ci)

9 for每个状态sbdo：

10 A在DA上计算类ci中sasb出现的次数

numB(aa,sb,ci)

11 B在DB上计算类ci中sasb出现的次数

numB(sa,sb,ci)

12 endfor

13 endfor

14 endfor

15 A、B各自计算上面计算的所有次数对应的加密参数，B将计算的参数发送给A，A利用B的参数计算获得最终模型.

3.2 K阶马尔可夫模型

K阶马尔可夫模型与一阶马尔科夫模型类似，但需将每个状态的关联状态向前进行了拓展，所以K阶马尔可夫模型的需要计算更多的参数.

对于每一个K长度的序列：s1,s2,…,sk，对于每一个类ci，先验概率为：

上式中num(s1,s2,…,sk,ci)表示类ci中串s1,s2,…,sk出现的次数，num(所有K长度序列)表示串ci中所有K长度序列的数量.

对于任何一个状态si以及k长度串：s1,s2,…,sk，状态si到s1,s2,…,sk的转移概率为：

K阶马尔可夫对应的训练方案与一阶马尔可夫模型的训练方案基本一致，不同点为需要计算的模型参数数目会根据K变化，需要计算更多的先验概率和转移概率.

4 试验及结果分析

4.1 实验环境及相关说明

使用单核CPU主频为2.4GHz，内存为512M，运行Ubuntu 16.04系统的主机.使用C++进行编程，借助Crypto++库和Linux Socket.

实验数据为人和老鼠的基因数据，数据由1提供的链接下载，数据为真实数据.根据数据的特点，为方便实验，对数据进行了预处理.对缺失数值采取删除处理，并去除一些无用信息后将数据整理成每行最多20个，最少18个.根据对实验的相关参数的分析，将数据组织成20、100、200、1000行四个训练数据集，标记为D1、D2、D3、D4.

为综合评估本方案，从方案的误差、时间效率以及与类似方案的对比进行分析.

4.2 误差分析

此处误差是指多方合作训练马尔科夫模型与单独在数据集上训练马尔科夫模型所获得的两个模型的误差.

由理论分析可知，使用此方案训练的马尔科夫模型没有误差.但是实际实验中仍然可能产生误差.对过程分析可知需要计算H(t)k这个参数，其中所有K相加为0，故存在K为负数，此时H(t)k为实数，实数运算中就会产生误差.为了避免此类误差，有两种解决方法，一种是对所有K加一常数，使其为非负数，另一种方法是将K当成其绝对值，然后标记计算结果，改进计算方式.本实验使用第二种方法.经过实验验证，本方案在所选的数据集上合作训练马尔科夫模型与单独训练马尔科夫模型相比无误差.

4.3 时间效率

方案的时间效率主要考虑整体时间开销，以及模型训练各阶段的时间开销.

表1 一阶运行时间实验结果Table 1 Experimental result of running time with order 1

对方案的时间效率进行分析，设计两组实验.第一组实验主要测试不同参数以及不同数据集上实验的时间开销.参数主要有群的阶的位数、可信第三方分发的密钥位数以及马尔科夫模型阶数，实验只训练一轮.实验结果如表1表2所示，实验结果中时间单位为秒.

表2 二阶运行时间实验结果Table 2 Experimental result of running time with order 2

从表1表2可以看到，在其它参数相同的条件下，马尔科夫模型阶数、群的阶的位数、密钥的位数、数据集的规模分别增长时，训练模型的时间开销都会增长.此实验只进行一轮，可以看出只有一轮的情况下，有些参数情况时时间开销较小，实际使用的可行性较高.

第二组实验主要探索模型训练各阶段时间开销，将模型训练过程分为三阶段：可信第三方生成及分发密钥等参数、各方本地训练并发送数据给最终模型训练者、最终模型训练者计算模型，三阶段依次记为T1、T2、T3.群G的阶为2048位，密钥长度为8位.实验结果如表3所示，实验结果中时间单位为秒.

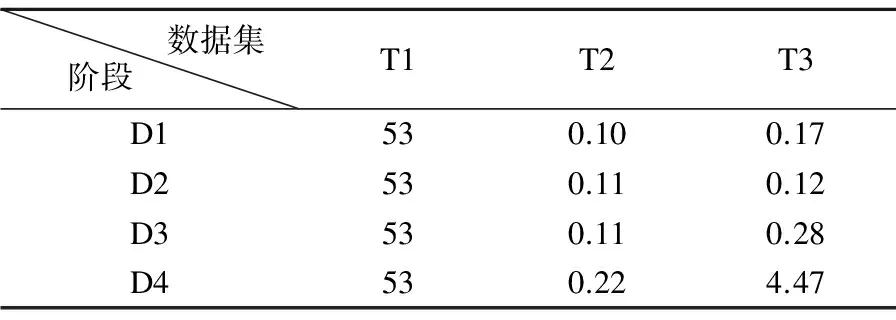
表3 各阶段时间实验结果Table 3 Experimental result of time cost in every period

从表3可看到T1阶段的时间开销最大，其他两个阶段时间开销比较小.如果是多轮训练，则只会增加T2和T3阶段，时间开销增长较少，所以随着轮数增加，本方案优势较高.需要指出的是本实验中群的阶为2048位，当群的阶为1024位时，则T1会有较大幅度的较少，同理，如果将群的阶设置为4096位，在本实验环境中花费六分钟以上仍未完成T1阶段.从本实验结果可以看出，虽然T1时间较长，但是T2、T3比较小，实际使用有较高的可行性.

4.4 比较与分析

目前隐私保护的马尔科夫模型训练方案还有同态加密方案[2].其主要借助于secure logsum协议，其实验中使用ElGamal加密系统作为同态加密工具.本实验数据集D1与同态加密方案测试的第一个数据集的数量相比近似相同，此处将使用其实验数据与本文方案做比较.实验结果如图1所示，柱状体的高度表示时间开销，单位为秒.

图1 两种方案时间开销Fig.1 Time cost of two method

从图中可以看出，随着轮数增加，本文方案具有较小的增长，同态加密方案则是增加一个固定的数值.通过对两个方案进行比较可以知道，两个方案使用了类似的技术，而从分层的角度看，同态加密方案有两层，而本文方案只有一层，本文方案对本问题具有更强的针对性，同态加密方案有较高的通用性.

4.5 实验总结与改进

本实验模拟了在保护各参与方数据隐私的前提下合作训练马尔可夫模型的方案.误差分析说明了方案的正确性，时间效率实验指出本方案具有较高的可行性，与已有方案的比较试验证明了本方案具有较高的时间效率优势.

通过对方案分析和对实验结果进行探究可以对本方案进行加强和改进，例如在程序流程上可以探索各方合作时如何针对不同的数据集调整训练流程，减小训练时间.另外在某些数据量比较大的时候可以考虑把单个参与方虚拟为多个参与方，将数据均分到虚拟参与方，减少单个参与方在计算大数时的较高开销.

5 工作展望

本文首先介绍了用于序列数据分类的马尔科夫模型，然后介绍了隐私保护的马尔科夫模型，进而提出了一个在隐私保护情况下训练马尔科夫模型的方案，并针对提出的方案进行实验. 实验结果显示此方案具有比较好的准确度和相对较小的开销.后面将会探索对实验方案进行改进，在可信第三方发放密钥之后，将研究密钥随着时间变化，每个参与方的密钥将会有一个以初始密钥作为输入的函数产生，所有参与方的密钥都会随着时间变化，但是仍然保持所有参与方密钥之和为零的特性.还将探索如何利用现代计算机特性，提高运算效率.

[1] Shi E，Chan H T H，Rieffel E，et al.Privacy-preserving aggregation of time-series data[C].Annual Network & Distributed System Security Symposium(NDSS)，Internet Society，2011.

[2] Guo S，Zhong S，Zhang A.A privacy preserving Markov model for sequence classification[C].Proceedings of the International Conference on Bioinformatics，Computational Biology and Biomedical Informatics，ACM，2013：561.

[3] Jha S，Kruger L，Shmatikov V.Towards practical privacy for genomic computation[C].Security and Privacy，SP 2008，IEEE Symposium on.IEEE，2008：216-230.

[4] Tan Pang-ning，Michael Steinbach，Vipin Kumar.Introduction to data mining[M].Beijing：Beijing Posts and Telecom Press，2011.

[5] Andorf C，Silvescu A，Dobbs D，et al.Learning classifiers for assigning protein sequences to gene ontology functional families[J].Structural Induction：Towards Automatic Ontology Elicitation，2008：39.

[6] Chen K，Liu L.Privacy preserving data classification with rotation perturbation[C].Data Mining，Fifth IEEE International Conference on.IEEE，2005：589-592.

[7] Agrawal R，Srikant R.Privacy-preserving data mining[C].ACM Sigmod Record，ACM，2000，29(2)：439-450.

[8] Huang Z，Du W，Chen B.Deriving private information from randomized data[C].Proceedings of the 2005 ACM SIGMOD International Conference on Management of Data，ACM，2005：37-48.

[9] Du W，Zhan Z.Building decision tree classifier on private data[C].Proceedings of the IEEE International Conference on Privacy，Security and Data Mining-Volume 14，Australian Computer Society，Inc.，2002：1-8.

[10] Lindell Y，Pinkas B.Privacy preserving data mining[C].Annual International Cryptology Conference，Springer Berlin Heidelberg，2000：36-54.

[11] Yan Cai-rong，Zhu Ming，Shi You-qun.Mining sequential patterns based on privacy preserving [J].Journal of Chinese Computer Systems，2008，29(7)：1241-1244.

[12] Lu Cheng-lang，Liu Ming-yong，Wu Zong-da，et al.Personal privacy protection scheme for network information systems[J].Journal of Chinese Computer Systems，2015，36(6)：1291-1295.

[13] Lin Shao-cong，Ye A-yong，Xu Li.K-anonymity location privacy protection method with coordinate transformation[J].Journal of Chinese Computer Systems，2016，37(1)：119-123.

[14] Qian Ping，Wu Meng，Liu Zhen.A method on homomorphic encryption privacy preserving for cloud computing[J].Journal of Chinese Computer Systems，2015，36(4)：840-844.

[15]Xu Wei-jiang，Huang Liu-sheng，Luo Yong-long，et al.Privacy-preserving range searching [J].Journal of Chinese Computer Systems，2009，30(10)：1972-1979.

附中文参考文献：

[4] Tan Pang-ning，Michael Steinbach，Vipin Kumar.数据挖掘导论[M].北京：人民邮电出版社，2011.

[11] 燕彩蓉，朱 明，史有群.基于隐私保护的序列模式挖掘[J].小型微型计算机系统，2008，29(7)：1241-1244.

[12] 卢成浪，刘明雍，吴宗大，等.针对网络信息系统的个人隐私保护方案[J].小型微型计算机系统，2015，36(6)：1291-1295.

[13] 林少聪，叶阿勇，许 力.基于坐标变换的k匿名位置隐私保护方法[J].小型微型计算机系统，2016，37(1)：119-123.

[14] 钱 萍，吴 蒙，刘 镇.面向云计算的同态加密隐私保护方法[J].小型微型计算机系统，2015，36(4)：840-844.

[15] 徐维江，黄刘生，罗永龙，等.保护私有信息的范围搜索算法[J].小型微型计算机系统，2009，30(10)：1972-1979.