基于集成相关向量机的水质在线预测模型
,,
(1.华南理工大学 机械与汽车工程学院,广东 广州 510640;2.广州中国科学院 沈阳自动化研究所分所,广东 广州 511458)
0 引言
污水处理过程工况复杂,在线测量仪表维护成本高昂,存在着如毒性物质浓度、化学需氧量(chemical oxygen demand, COD)、氨氮、生化需氧量(biological oxygen deman, BOD)等难以在线测量的水质指标,而污水处理中各设备间的自动化控制与调度依赖于水质的实时准确测量[1]。现有的常用水质测量方法有减压库伦法、离线分析法、活性污泥快速法、标准稀释法等,水质的测定周期较长,不能及时的提供污水处理的实时信息,为污水处理的实际生产带来不便。预测水质的变化趋势对于掌握污水处理现状具有重要意义,然而影响水质变化的因素众多,各因素间又相互影响,传统方法依托建立精确的生化机理反应模型的来预测水质变化,难以克服各因素间的强非线性,预测误差较大。面对这些特点,国内外学者提出了大量基于数据驱动的污水水质指标软测量方法,该方法无需了解污水生化反应过程中的复杂机制,根植于数据本身,极大的促进了污水处理水质预测的研究。文献[2-3]采用神经网络建立污水水质预测模型,文献[4-5]采用支持向量机建立了污水处理过程出水水质的软测量模型,文献[6]采用相关向量机建立了污水水质的在线软测量预测模型,并引入快速似然边界算法加快了模型的更新速度。然而,神经网络容易陷入局部最小值和过拟合,存在着健忘和泛化性能较弱,权值不易在线调整等缺点[7],支持向量机随着样本量的增加,训练时间会变长,支持向量增多,稀疏性降低,且核函数的选择受到Mercer条件制约[8],当样本中存在较少异常值时,相关向量机可以得到鲁棒性良好的回归模型[9],但随着异常值的增多,其泛化能力会下降,鲁棒性渐失,同时这些缺陷均影响了污水水质在线预测的可靠性和实时性。
根据现有成果与存在的问题,本文提出一种基于集成相关向量机的污水水质在线预测模型。该模型以RVM为弱预测器,利用改进的AdaBoost.RT算法将多个弱预测器集成为强预测器。RVM是建立在贝叶斯理论(Bayesian Principle)下的稀疏核机,不受Mercer定理的限制,可以任意选择核函数,具有较好的泛化能力,但污水生化处理的过程,存在着参数时变的现象,随着异常值的增多,会使RVM的预测精度下降,针对这一问题,该模型利用改进的AdaBoost.RT算法将RVM弱预测器分层组合,使迭代的重点聚焦与少数异常样本上,提高了模型的预测精度的鲁棒性,同时也满足污水水质在线预测的实时性的要求,并通过仿真实验得到了验证。
1 基于集成相关向量机的水质在线预测模型
1.1 相关向量机回归模型

tn=y(xn,w)+εn
(1)
其中:权值向量w=(w0,w1,···,wn),εn为期望为0,方差为σ2的附加高斯噪声,即εn~N(0,σ2)。因此p(tn|x)=N(tn|y(xn),σ2),式中y(x)定义为:
(2)
式中,K(x,xi)为核函数。其中常用的全局性核函数有多项式核函数,如式(3)和常用的局部性核函数有径向基核函数,如式(4)。
K(x,y)=(xTy+c)q,q∈N,c≥0
(3)
(4)
其中:c为常数,q表示多项式次数,δ为核宽度。
由于tn是相互独立的,因此训练样本集的似然函数为:
(5)
其中:t=(t1,t2,···,tn)T,Φ=[φ(x1),φ(x2),···,φ(xn)]T,φ(xn)=[1,K(xn,x1),···,K(xn,xT)]T。
为避免RVM回归模型出现过度拟合(over-fitting),RVM定义一个高斯先验概率来约束权值向量w:
(6)
其中:超参数α=(a0,a1,…,aN)T,由式(6)可以看出每一个权值wi对应唯一的超参数αi,参数受到先验分布的影响,通过对样本集的不断训练,大部分超参数αi将趋于无穷大,其对应的权值wi会趋于0,从而确保了相关向量机的稀疏性。
根据贝叶斯准则,定义了先验概率,可得到后验概率:
(7)
当输入一个新样本x*,预测相应输出t*预测分布为:
(8)
也可以得到权重w的后验概率分布为:
(9)
其中后验协方差∑和均值μ分别为:
∑=(σ-2ΦTΦ+A)-1
(10)
μ=σ-2∑ΦTt
(11)
式中,A=diag(α0,α1,···,αN)。基于最大期望超参数估计,多次迭代计算后可得:
(αi)new=γi/μi2
(12)
(13)
式中,μi为第i个后验平均权值;γi定义γi≡1-αi∑ii。
(14)
其中:
(15)
y*=μTΦ(x*)
(16)
式中,y*为t*的预测值。
1.2 改进的AdaBoost.RT算法
集成算法[11]的基本思想是将多个仅比随机猜测略好的弱预测器进行迭代融合从而使得到的强预测器具有更高的预测精度和泛化能力。与传统的集成算法AdaBoost相比,AdaBoost.RT算法的主要区别在于引进了固定阈值φ,通过与训练误差的对比,确定权值更新的方式,它解决了最初boosting算法在训练集中损失函数超过0.5便停止和不能任意设置迭代次数的缺陷。AdaBoost.RT算法的具体计算过程如下:
1)输入:m个样本、弱预测器算法ft、迭代次数T、阈值φ(0<φ<1)。
3)训练:当t Et=|(ft(xi)-yi)/yi| (17) 根据式(18)计算弱预测器ft的误差率: (18) (19) 式中,Zt是归一化因子。 4) 输出预测结果:结果T轮的训练后的得到的强预测器F由T个弱预测器根据误差率加权平均得到,如式(20)。 (20) 由上述计算步骤可以看出,AdaBoost.RT算法性能对于阈值φ的选择比较依赖,若阈值φ的取值过大将难以实现对异常数据的重点学习,若取值过小则无法将足够的样本进行充分的学习,实际应用中通常需要反复实验才能最终确定阈值φ的取值,阈值φ的取值对于模型的性能至关重要。针对这一问题,对AdaBoost.RT进行改进:将固定的阈值φ改为自适应型阈值,使阈值φ在集成学习的过程中根据误差的变化而变化,即当误差εt大于误差εt-1时,增大阈值φ,当误差εt小于误差εt-1时,减小阈值φ,加强了对难以预测的样本的学习,最终提高了模型最终的预测精度和泛化能力。具体做法是在每次迭代计算后,计算弱预测器的均方根误差(root mean square error, RMSE),如式(21): (21) 然后按式(22)对阈值φ进行调整: (22) 其中:α的计算公式为: (23) 所以,样本权重的更新公式在改进AdaBoost.RT算法中被修改为: (24) 文献[12]指出,当改进的AdaBoost.RT算法的阈值φ初始设置大于0.4时,模型对阈值φ的变化十分敏感,预测误差变化较大,模型的鲁棒性不足,而当初始阈值φ设置在(0,0.4)之间时,模型的预测误差输出较为稳定,也较好地避免了模型训练过程中阈值φ陷入局部最优。 污水处理具有复杂的生化反应过程和非稳态运行等特征,不同的水质指标受到不同的特征的影响,本文以预测生化需氧量BOD为例,建立水质在线预测模型。BOD定义为20℃时,污水中好氧微生物将有机污染物氧化分解时所需氧气量,是反应污水中可降解有机物的指标,BOD越大则污染情况就越严重[13]。根据BOD的特性选择与之相关联的水质特征组成数据集,为消除不同特征间幅值对预测精度的影响,对污水水质数据进行归一化处理。在线仿真实验中模型更新时,为保持训练样本集的容量不变,选择限定记忆法来确保每次都有新的样本增加,同时删除最早的样本数据。基于集成RVM的水质预测模型流程简图如图1所示。 图1 集成RVM模型建模流程图 本文所用污水处理过程数据来源于加州大学欧文分校机器学习数据库,数据为某城市污水厂2年间实际生产所测得数据,采样时间最大间隔为2天,共包含527个样本,每个样本具有38个特征,其中不含缺失值的样本有380个,具有13种运行状态。进行数据预处理时,将数据集中不满足3σ原则的异常值所在样本和具有缺失值的相邻样本删除,然后对缺失值进行拉格朗日插值填补。选取与BOD相关的输入特征,分别为整个污水厂的BOD输入、COD输入、悬浮固体浓度和可降解固体浓度,初沉池的BOD和固体悬浮物浓度Ss,二沉池的BOD和COD,二级沉降器BOD、COD、pH、固体悬浮物浓度和可降解固体浓度以及输出的COD、BOD、悬浮固体浓度与可降解固体浓度,最终得到420组样本数据。 污水处理过程的水质预测本质是一个回归问题,为评价各水质预测模型的综合性能,采用均方根误差RMSE,平均相对误差mean-re,最大相对误差max-re和每次模型更新的平均用时time四个指标作为模型综合性能的评价标准。其中: 仿真实验中计算机环境为:Windows 10操作系统,Intel Core i5处理器,主频为3.2 GHz,8 G内存,240 G固态硬盘,采用Matlab 2016b软件编程实现。选取最终得到的420组污水水质的样本数据,其中320组用于模型的训练,余下的100组作为测试集来验证模型的综合性能。分别建立基于支持向量机SVM、相关向量机RVM和集成相关向量机RVM的水质指标BOD的在线预测模型。所建模型均采用径向基核函数,如式(4)。SVM的惩罚参数c和核参数g1采用五折交叉验证和遗传算法寻优确定,RVM与集成RVM的核参数g2与g3亦采用五折交叉验证法和遗传算法寻优确定,g3由首次寻优确定后,在后续弱预测器的迭代中不变,集成RVM模型的弱预测器个数设置为5个。其中,SVM模型的预设迭代次数为300次,RVM模型的预设迭代次数为500次,原因在于SVM的目标函数是一个凸二次规划求解问题,而RVM模型的目标函数非凸需要更多的迭代次数,考虑到集成RVM的迭代所需为弱预测器,其迭代次数预设为300次。 进行后续水质在线预测时,采用同上述一样的步骤方法以及限定记忆法对模型进行更新。本文中各模型的仿真实验均进行10次,得到的数据为10次实验结果的平均值,3种模型的水质在线预测性能评价指标如表1所示,图2~图4分别为BOD的实际数据与各模型的预测结果对比图。 表1 3种模型的水质预测结果 注:RVM-A表示集成RVM模型 从表1中可以看出,在具有强非线性和非稳态和参数时变的污水处理环境中,集成RVM模型的预测精度最高,均方根误差RMSE为1.857,平均相对误差mean-re为0.076,最大相对误差max-re为0.278,相较于单一预测器的RVM和SVM模型,均方根误差RMSE分别下降了19.5%和20.9%,平均相对误差mean-re分别下降了30.9%和26.2%,最大相对误差max-re分别下降了52.0%和22.6%。 图2 SVM在线预测结果 图3 RVM在线预测结果 图4 集成RVM在线预测结果 在3种水质预测模型中,SVM的训练时间最长,原因在于SVM有惩罚系数c和核宽度g两个参数需要寻优确定,而RVM仅需寻优确定核宽度一个参数,RVM的惩罚系数c会在训练过程中自动生成,而在SVM中惩罚系数c是平衡经验风险和置信区间的重要参数,需要人工设置,显然一维参数比二维参数寻优的时间复杂度要小很多[14]。由于RVM比SVM的稀疏性更好,在训练与预测中,RVM极大地降低了核函数的计算量,模型训练完成后,对于新样本的预测所需要时间也更短。 从图2~图4中各模型的预测对比图可以看出,集成RVM模型对于BOD的变化追踪效果最好,能更好的适应新的工况,具有最佳的模型鲁棒性和泛化性能。图5为集成RVM模型和RVM模型的预测绝对误差对比图,可以看出:集成RVM模型对于绝大多数测试样本的预测误差低于单一RVM模型,特别是对异常样本的预测,集成RVM在多轮的迭代过程中针对异常值的重点学习在此情况下体现出了极大的优势。从表1可以看出,集成RVM的模型更新速度比RVM模型慢,原因在于多出了集成多个弱预测器的过程,从实际污水处理过程中对水质在线预测的要求考虑,模型的预测精度和泛化能力的优先级要略高于模型对时间的要求。 图5 绝对误差对比图 结合以上分析,基于集成RVM的污水处理水质在线预测模型的综合性能优于其他模型,满足实际污水处理过程中对于水质预测准确性和实时性的要求。 污水处理是一个复杂的生化反应过程,具有强非线性和参数时变等特征,传统的传感器难以测量BOD等反应水质情况的关键指标,并考虑到单一弱预测器难以在异常值增加的情况下获得良好的预测精度和鲁棒性,因此本文提出一种基于改进AdaBoost.RT算法集成相关向量机RVM的污水处理水质在线预测模型。通过与SVM和RVM预测模型的对比,仿真实验结果表明:集成RVM模型具有预测精度高,能够很好的适应BOD的变化,同时模型更新速度快,在异常值增多的情况下依然具有良好的鲁棒性等优点,较好地克服了复杂的污水处理环境带来的困难,完全满足水质在线预测的实际要求。 [1] 黄道平, 刘乙奇, 李 艳. 软测量在污水处理过程中的研究与应用[J]. 化工学报, 2011, 62(1): 1-9. [2] 张瑞成,王 宇,李 冲. 基于NW型小世界人工神经网络的污水出水水质预测[J]. 计算机测量与控制, 2016, 24(1): 61-63. [3] Pai T Y, Wan T J, Hsu S T, et al. Using fuzzy inference system to improve neural network for predicting hospital wastewater treatment plant effluent[J]. Computers & Chemical Engineering, 2009, 33(7): 1272-1278. [4] 黄银蓉, 张绍德. MIMO最小二乘支持向量机污水处理在线软测量研究[J]. 自动化与仪器仪表, 2010, 30(4):15-17. [5] Chen Z M, Hu J. Wastewater treatment prediction based on chaos-GA optimized LS-SVM[C]./Proceedings of the 2011 Chinese Control and Decision Conference. Mianyang: China Academic Journal Electronic Publishing House, 2011: 4021-4024. [6] 许玉格, 刘 莉, 曹 涛. 基于Fast-RVM的在线软测量预测模型[J]. 化工学报, 2015, 66(11): 4540-4545. [7] 冉维丽, 乔俊飞. 基于PCA时间延迟神经网络的BOD在线预测软测量方法[J]. 电工技术学报, 2004, 19(12): 78-82. [8] Pani A K, Mohanta H K. Application of support vector regression, fuzzy inference and adaptive neural fuzzy inference techniques for online monitoring of cement fitness[J]. Powder Technology, 2014, 264: 484-497. [9] 杨 飚, 周 阳. 一种改进的相关向量机回归方法[J]. 科学技术与工程, 2015, 15(2): 241-245. [10] TIPPING M E. Sparse Bayesian learning and the relevance vector machine[J]. Journal of Machine Learning Research, 2001, 1(3): 211-244. [11] 毛志忠, 田慧欣, 王 琰. 基于AdaBoost混合模型的LF炉钢水终点温度软测量[J]. 仪器仪表学报, 2008, 29(3): 662-667. [12] Solomatine D P, Shrestha D L. AdaBoost.RT: A boosting algorithm for regression problems[C].IEEE International Joint Conference on Neural Networks, Piscataway, 2004: 1163-1168. [13] Yu G P, Yuan M Z, Wang H. On simplified model for activated sludge wastewater treatment process and simulation based on benchmark[C].Proceedings of the 26th Chinese Control Conference, 2007: 182-186. [14] Masuda K. Global optimization of point search by equilibrium search of gradient dynamical system [J]. Electronic and Communication in Japan, 2008, 91(1): 19-31.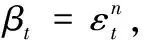
1.3 建模步骤

2 实验仿真与结果分析
2.1 实验数据
2.2 性能评价指标
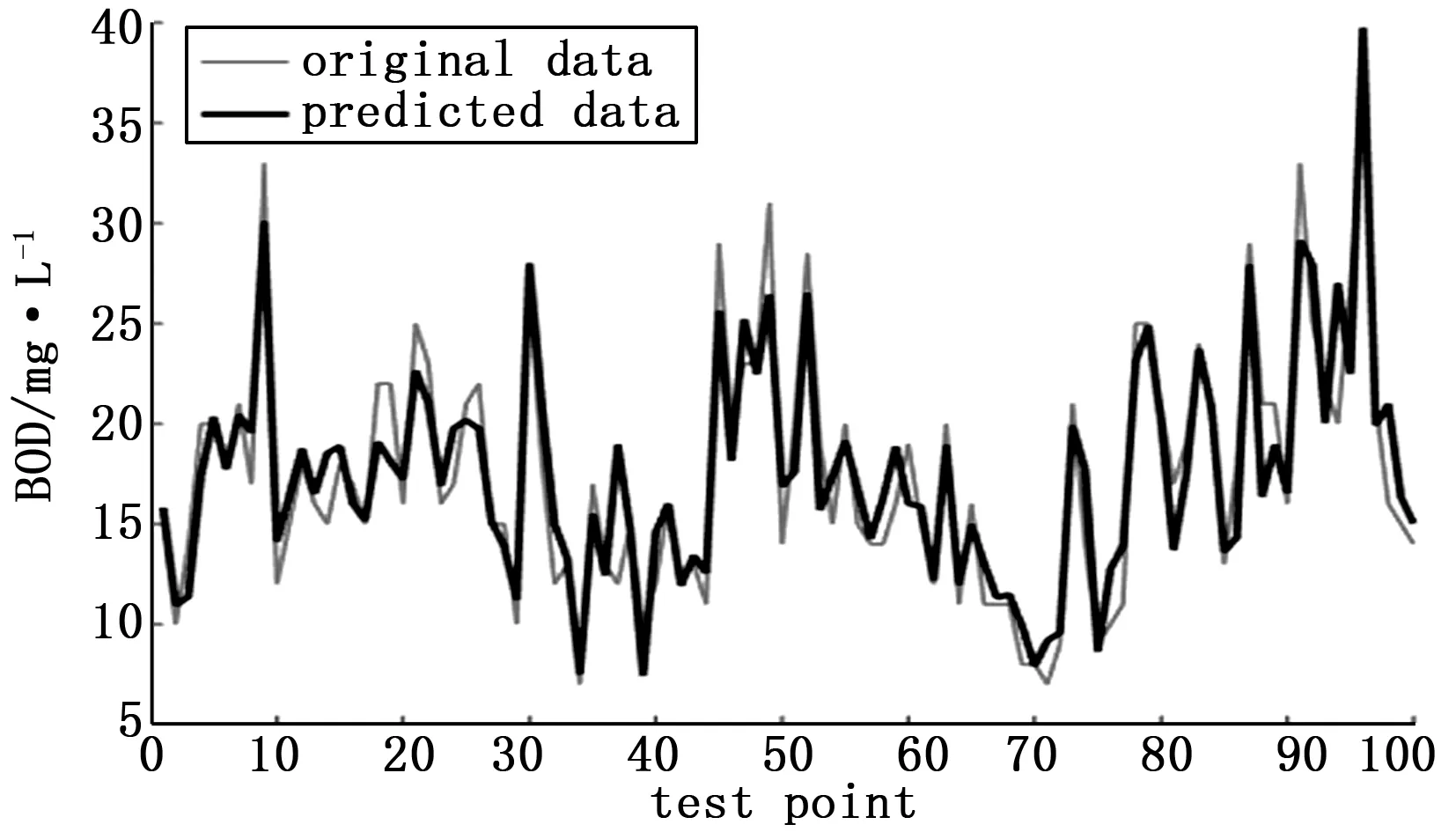
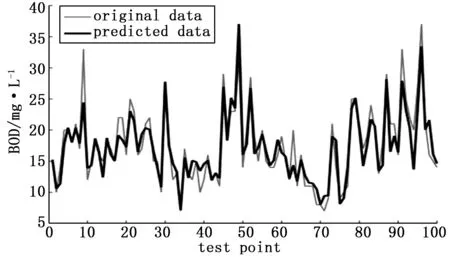
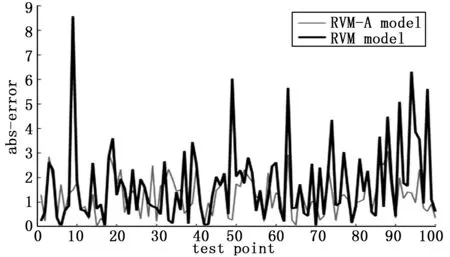
2.3 在线仿真实验


3 结论

