多精英协同进化遗传算法求解外卖送餐路线优化问题
刘竞遥,赵欢欢
滁州学院计算机与信息工程学院, 滁州,239000
随着信息化时代的到来,传统的餐饮业已经慢慢向O2O方式靠拢,商家通过第三方订餐软件获取订餐信息,实时配送。对于商家来说,服务员接待和打扫卫生的成本减少了,但却增加了配送成本,需要雇佣专门的送餐人员。针对订餐源广、配送不及时的情况,提出一种多商家联合成立送餐队、集中配送、统一管理的方法。并且在就餐高峰期雇用临时工,可大大节约成本。送餐过程中采用遗传算法进行路径优化,再次节约时间,提高效率。
带时间窗的路径优化问题(VRPTW)是一个NP问题[1],顾客有一个等待时间约束,在规定时间内送餐队统一分配送餐任务,每个小区随时都可能有订单产生,送餐员在有限的时间内送出最多的外卖,就能节约劳动成本,每个送餐员送完一趟回来还可以继续接单送餐。城市外卖送餐路径问题目标是寻找雇佣人员最少、利润最大、等待时间合理的方案。由此,本文提出了一种基于多精英协同进化遗传算法求解城市外卖送餐路径优化问题的方案。
1 多精英协同进化遗传算法
遗传算法解决实际寻优问题的能力强大、发展迅速并且受到人们的普遍关注,自其确立以来就成立了每两年一届的国际遗传算法学会。遗传算法的相关研究在各大杂志上屡有发表,并且研究成果显著。
目前遗传算法已经广泛应用于模糊模式识别、人工生命、进化神经网络等领域。但是,传统的遗传算法也有它的缺陷:优化不够彻底、收敛速度慢、易于陷入早熟收敛等问题[2]。而多精英协同进化遗传算法(简称MCGA)主要运用了精英策略和协同进化的思想,在优良的精英个体被保存的情况下,不断地从其他个体中进化出精英个体并再次被保存。通过不同的选择策略进化子种群,多个子种群采用不同的进化方式[3]。实验数据表明,该种多精英协同进化遗传算法每一次运行都能寻找到最优解,并且用时短,提高了收敛速度,操作简单,多样性图示表明该种遗传算法还增加了种群多样性,可以跳出局部最优解,提高寻优能力。传统的遗传算法操作流程:(1)采用二进制编码方式对问题进行描述;(2)随机产生n个个体的种群;(3)设置适应度函数并且通过计算适应度值进行个体评价;(4)用轮盘赌选择法选择个体进行进化,个体的选择随机并可以重复;(5)通过对交叉概率判定进行单点交叉;(6)通过变异算子进行变异;(7)寻找最优解。
多精英协同进化遗传算法流程如图1所示。
用多精英协同进化遗传算法和传统遗传算法(SGA)对多个函数进行测试比较,运行参数一致,交叉概率(pc)为0.6,变异概率(pm)为0.01,测试使用如下函数:

图1 多精英协同进化遗传算法流程图
种群大小为70,最大进化代数为150代,基因长度为20位二进制数[4]。对同一种函数分别用两种方法各仿真60次。MCGA对函数f1求解成功57次,SGA求解成功26次。图2为两种算法的平均适应度值比较。可以看出,在进化过程中,SGA比MCGA平均适应度值进化快。图3、图4、图5为种群多样性统计数据对比。可以看出,MCGA种群多样性比SGA好,不容易陷入区域极值,容易得到最优解,MCGA的best收敛速度相对更快一些。
与双精英协同进化遗传算法(DECGA)[5]相比,MCGA对函数的平均收敛代数优于DECGA。因此多精英协同进化遗传算法在传统遗传算法的基础上有了较大改进,能快速找到最优解,对子种群进行分组,不同的分组采用不同的交叉策略,使各个分组都拥有种群多样性的特点,又能提高进化速度。




2 问题描述
城市外卖送餐路径问题可以描述如下:
有n个订单m个送餐员,每个送餐员每次去送一次餐回到原点,然后再次出发,每个送餐员最多送餐量为Q,订单点编号为i(i=1,2,3,…,n),dij为i订单点在j时刻产生的订单,wij为i订单最晚配送时间,sij为i到j的送餐时间,其中sij 定义变量如下: 此问题的数学模型: minz=xwijyijw (1) 约束条件: Ywi=1 (i=0,1,…,n) (2) 其中,式(2)表示每一份外卖只能有一个送餐员派送。 外卖送餐路线VRPTW问题按照订单产生的先后顺序用整数表示,原点用0表示,订单点p用1,2,3…n表示。送餐员x用1,2,3…m表示,每次订单从送餐员列中随机选择序号,形成n个由m数中抽取组成的路径。 通过对每个订单产生的时间及送餐员速度路程的合理判断形成了点到点的路径,将一段时间内的点分成组,本组只能跟前一组和后一组的个体相连,这样就省去了相隔时间过长的两个个体进行连接,也就不会有订单有过长时间的等待。根据事件发生时间先后个体本身事件发生后,其后边的个体事件才可以发生,整个路径合理则作为初始种群。如图6所示。 图6 4个送餐员外卖送餐路径AOE路径图 第一组优良精英组进行单点交叉,可以把优秀个体的性状遗传给下一代的同时又有新个体产生。单点交叉运算如下所示: 交叉前 :Aa0,a1,a2,a3,a4,a5,a6,a7,a8,a9 Bb0,b1,b2,b3,b4,b5,b6,b7,b8,b9 第二组使用两点交叉,运算如下所示: 交叉前 :Aa0,a1,a2,a3,a4,a5,a6,a7,a8,a9 Bb0,b1,b2,b3,b4,b5,b6,b7,b8,b9 第三组最差组我们选择逆转交叉,交叉后实现逆转,逆转后个体差异大,可以尽量多的产生新个体,增加种群多样性,跳出局部最优解得到适应度值高的个体[2]。逆转算子交叉运算如下所示: 交叉前 :Aa0,a1,a2,a3,a4,a5,a6,a7,a8,a9 Bb0,b1,b2,b3,b4,b5,b6,b7,b8,b9 变异是在满足变异概率的情况下随机生成两个位置,将两个位置上的基因交换。例如: 变异前:Aa0,a1,a2,a3,a4,a5,a6,a7,a8,a9 对6家附近的餐厅联合配送,总共有10个订餐小区点,时间从11:00点开始记为0,后一个小时进行统计,订餐高峰期第一、二个订餐点每隔60分钟产生一个订单,第三个订餐点每隔65分钟产生一个订单,第四、五个订餐点每隔70分钟产生一个订单,第六、七个订餐点每隔80分钟产生一次订单,第八个订餐点每隔90分钟产生一个订单,第九、十个订餐点每隔100分钟产生一个订单。这样就会有87个订单,把每一个订单作为一个个体,按照产生时间早晚进行顺序排序,通过每个点距离原点(餐厅)的距离和食物加工时间可以求得当前订单滞留时间。各个订餐点离原点的距离位置如图7所示。 种群大小为50,最大进化代数为50代,图8为6辆车完成运输任务情况下MCGA和SGA路径安排下的食物滞留时间对比;图9为使用MCGA进行路径优化后分别用4、6、8、10个电动车完成送餐后店铺的收入情况对比。 本文通过具体的实例数据证实,进行集中配送要比每个商店雇佣专门配送人员更符合实际要求,并且多精英协同进化遗传算法在寻找到最优路径时比传统的遗传算法更加省时省力,所以应该选择MCGA进行路径优化。通过数据可以看出,在保证规定时间内送到的前提下,采用多精英协同进化遗传算法,为商店节省了一笔可观的人力开支。 图7 订餐点离原点的距离位置图 图8 食物滞留时间对比 图9 不同车辆数送餐带来的收入情况对比3 多精英遗传算法求解
3.1 构造初始种群

3.2 多精英交叉策略

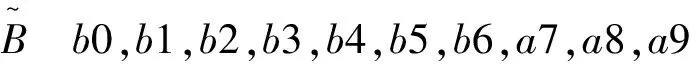




3.3 变异算子

4 仿真实验
5 结 论




