D2D通信中联合资源分配与功率控制算法

王全宇， 刘航宇， 潘昌杉

(兰州交通大学 电子与信息工程学院，甘肃 兰州 730000)

0 引 言

在蜂窝网络中引入终端直通(device to device,D2D)通信可以提高频谱效率(spectrum efficiency,SE)和能量效率(energy efficiency,EE)[1]，但却带来了很大的干扰和能量消耗。文献[2]为了缓解蜂窝用户对D2D用户的干扰，提出了一种限制蜂窝用户和D2D用户复用相同的资源之间的最小距离方案。文献[3]提出了一种干扰限制区域控制方案解决蜂窝用户与D2D用户之间的干扰。文献[4]优化了系统吞吐量并且引入二次竞争作为分配机制。上述研究主要通过使用资源分配改善性能。

功率控制也是实现高性能[5～9]的一个关键技术。文献[5]提出了一种功率控制方法，使信噪比降低到正常水平。文献[6]针对不同的资源共享模式提出了一种最优功率分配。文献[7]设计了一个新的分布式功率控制迭代算法，逐次分配目标信噪比(signal to noise ratio,SNR)和传输功率。文献[8]提出了一种将用户的要求的服务质量(quality of service,QoS) 作为约束条件的算法，最小化下行传输功率。文献[9]中提出了适用于D2D通信在长期演进(long term evolution,LTE)网络各种功率控制的策略。

许多无线系统目的在于提高频谱效率[10]。但是随着多媒体业务的增加，移动设备的功率消耗也随之大幅度增加，加上电池技术的发展缓慢，导致了未来的发展会更加注重EE。文献[11]提出了高效的功率控制方案,在3个不同的资源共享模式下达到最大传输功率。文献[12]提出了一个全局优化方案，同时兼顾模式选择、资源和功率分配，以达到最小化D2D通信功耗。文献[13]提出了一种低复杂性封闭功率控制和资源分配计划。对于现有的D2D通信研究，很少有方案将资源分配和功率控制二者兼顾起来。

本文制定了一个以D2D通信资源分配和功率控制问题作为核心的优化方案。利用分式规划的性质，将优化问题转化为一种容易处理解决的方案，然后通过迭代的方法获得最优解。在每次迭代中，利用补偿函数，部分优化问题的约束条件被消除。用一种联合资源分配和功率控制的方案最大化EE，收敛到最优解的速度较快。

1 系统模型和问题制定

图1中，列举了单小区系统模型。假设蜂窝用户(celluar users,CUs)上行资源被D2D资源对复用，所有的蜂窝用户和D2D用户随机分布在网络中。

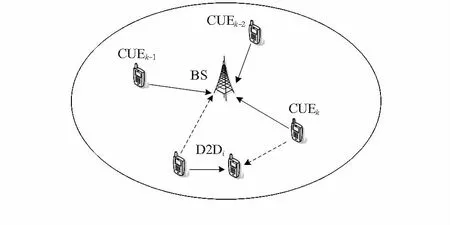
图1 系统模型

设L={1,2,…,Nc}，M={1,2,…,M},N={1,2,…,Nd}分别为蜂窝用户、资源块(resource blocks,RBs)以及D2D对的个数，并且Nc，M和Nd满足Nd≤Nc=M。设Pk,B为基站接收的来自蜂窝用户k的平均接收功率。Pk,B可以表示为

Pk,B=κPk,j(dk,B)-χ

(1)

式中Pk,j为第k个CUs发射第j个RBs的发射功率；dk,B为第k个CUs和基站(base station,BS)之间的距离;κ与χ分别为路径损耗常数和路径损耗指数。

设Pi,j为第i个D2D通信对发射第j个RBs时的发射功率，并且设R(Pi,j)为第i个D2D对传输第j个RBs数据时的速率。R(Pi,j)可以表示为

(2)

式中W为RBs的带宽；hi,j为在第i个D2D通信对从发送端到接收端获得的信道增益；hk,i为第k个CUs对第i个D2D对的接收端的信道增益;N0为噪功率。

为了达到高效率传输的目的，将所有的D2D通信对的EE作为优化目标。 设PC为所有被考虑到的D2D通信对的功率消耗。设UEE为所有的D2D通信对的EE，则

(3)

式中xi,j∈{0,1}。EE优化问题在数学上表示为

(4)

s.t.xi,j∈{0,1},∀i∈N,∀j∈M

(5)

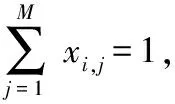
(6)

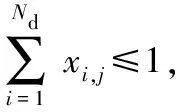
(7)

R(Pi,j)≥γi,∀xi,j=1

(8)

Pk,jhk,i≤τ,∀xi,j=1

(9)

Pi,j≤Pmax,∀xi,j=1

(10)

式中γi为每对D2D所需最小速率；τ为由于CUs与所对应D2D共享资源的允许的最大干扰；Pmax为每一对D2D发射机的最大传输功率。

2 联合资源分配和功率控制方案的提出

2.1 问题等价

首先将式(4)视为非线性规划，使Φ表示定义的可行域式(5)～式(10)。使q*表示D2D通信最大的EE，由文献[14～16]可知EE最大值q*能够取得，当且仅当

(11)

2.2 迭代算法

利用Dinkelbach迭代算法[14]，设S为迭代次数，qs为EE的瞬时值，ε为收敛阈值。Algorithm 复用模式下联合资源分配与功率控制算法:

1)初始化：

2)s=1,e=0；

4)如果|F(qs)|≥ε,设置s=s+1；

5)重复步骤(3)和步骤(4)直到|F(qs)|<ε。

令式Φ′表示式(8)～式(10)的可用区间，对应的优化问题可以被改写成

φ1Z1+φ2Z2}

(12)

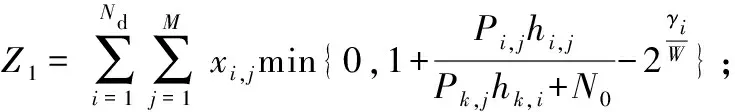
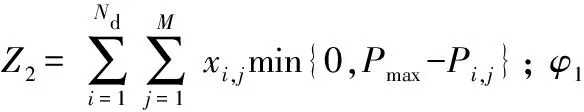
fi,j(Pi,j)=R(Pi,j)-qsPi,j+

亦式(12)可以表示成

(13)

2.3 联合资源分配和功率的控制方案

通过利用约束条件式(5)～式(7)，式(13)可等效为

maxPi,jfi,j(Pi,j)

只需将Pi,j与xi,j分别求出即可，并代入迭代算法中。

1)功率控制：

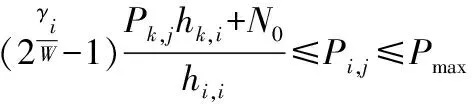
(14)

当qs≠0时，通过对fi,j(Pi,j)求Pi,j的导数，最优化传输速率

(15)

2)资源分配：

优化问题可以转换成

(16)

s.t.xi,j∈{0,1},∀i∈N,∀j∈M

(17)

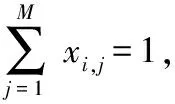
(18)

(19)

可以看出，上述xi,j的优化问题是一个典型的资源分配问题，可通过匈牙利解法或者分支界限算法解决[18]。

3 仿真结果

使用基于C++的系统级仿真器对所提出的算法进行了仿真分析[19]，具体参数设置：小区半径为500 m；D2D对内部距离为10，20，30，…，100 m;系统带宽为5 MHz；噪声功率密度为-114 dBm/Hz；RB带宽为180 kHz;蜂窝链路的路损模型为128.1+37.6lgd；D2D链路的路损模型为148+40lgd；蜂窝用户的最大发射功率为23 dBm；D2D用户的最大发射功率为20 dBm；D2D对数为4，8，12，16；蜂窝用户数为16；ε为10-4；PC为10 dBm。

图2给出了本文方法与文献[6,8]在性能上的比较。文献[6]采用最大化吞吐量方法。文献[8]通过迭代分配最小的功率增量达到最优解。可以看出：所提出的方法相比文献[6,8]显著提升了D2D EE。

图2 在不同方案下能量效率随着PB/N0的变化

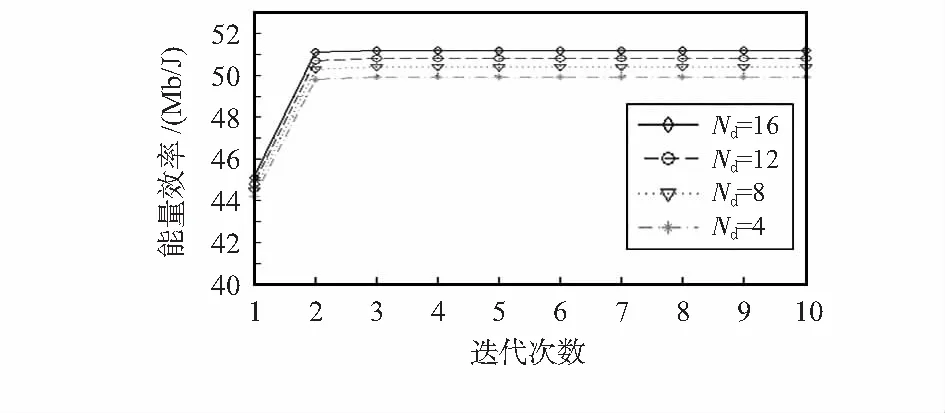
图3 不同D2D对数下能量效率与迭代次数关系

从图3中目标方案的EE与不同迭代次数Nd的关系看出，EE随着D2D的对数增加而增加,在此场景下，只需要用2次迭代即收敛到了最优的EE。

由图4可以看出：随着D2D用户距离的增加EE会降低。因为随着D2D使用者的距离的增长，衰落也随之增长。距离从10 m增加到100 m，能量效率下降了大约66 %，显然D2D内部之间的距离对目标算法的能量效率有着极大影响。

图4 不同D2D对数下能量效率与D2D用户距离关系

4 结束语

在移动蜂窝网络下提出了资源分配与功率控制的高能效的D2D通信，通过利用分式规划与补偿函数的性质，得到了一种高效迭代联合方案使D2D通信的能量效率最大化。仿真结果表明：方法在能量效率上有着显著的提高。

[1] 崔 鹏,陈 力.D2D技术在LTE-A系统中的应用[J].现代电信科技,2011(1):92-95.

[2] Wang H,Chu X.Distance-constrained resource-sharing criteria for device-to-device communications underlaying cellular networks[J].Electronics Letters,2012,48(9):528-530.

[3] Min H,Lee J,Park S,et al.Capacity enhancement using an interference limited area for device-to-device uplink underlaying cellular networks[J].IEEE Transactions on Wireless Communications,2011,10(12):3995-4000.

[4] Xu C,Song L,Han Z,et al.Efficiency resource allocation for device-to-device underlay communication systems:A reverse iterative combinatorial auction based approach[J].IEEE Journal on Selected Areas in Communications,2012,31(9):348-358.

[5] Doppler K,Yu C H,Ribeiro C B,et al.Mode selection for device-to-device communication underlaying an LTE-advanced network[J].IEEE Xplore,2010,29(16):1-6.

[6] Fodor G,Reider N.A distributed power control scheme for cellular network assisted D2D communications[C]∥Global Telecommunications Conference,GLOBECOM 2011,2011.

[7] Zhu X,Wen S,Cao G,et al.QoS-based resource allocation scheme for device-to-device (D2D) radio underlaying cellular networks[C]∥International Conference on Telecommunications,IEEE,2012:1-6.

[8] Fodor G,Della Penda D,Belleschi M,et al.A comparative study of power control approaches for device-to-device communicat-ions[C]∥2013 IEEE International Conference on Communications(ICC),IEEE,2013:6008-6013.

[9] Lei L,Zhong Z,Lin C,et al.Operator controlled device-to-device communications in LTE-advanced networks[J].IEEE Wireless Communications,2012,19(3):96-104.

[10] Shu F,You X H,Wang M,et al.Hybrid interference alignment and power allocation for multi-user interference MIMO channels[J].Science China Information Sciences,2013,56(4):1-9.

[11] Nguyen P B,Rao B.Through-put improvements for cellular systems with device-to-device communications[C]∥Asilomar Conference on Signals,Systems and Computers,2013:1973-1977.

[12] Kim S,Stark W.Full duplex device to device communication in cellular networks[C]∥International Conference on Computing,Networking and Communications,2014:721-725.

[13] Oduola W O,Li X,Qian L,et al.Power control for device-to-device communications as an underlay to cellular system[C]∥2014 IEEE International Conference on Communications ICC 2014:5257-5262.

[14] Ng D W K,Lo E S,Schober R.Energy-efficient resource allocation in multi-cell OFDMA systems with limited backhaul capa-city[J].IEEE Transactions on Wireless Communications,2012,11(10):1146-1151.

[15] Wu Q,Chen W,Tao M,et al.Resource allocation for joint transmitter and receiver energy efficiency maximization in downlink OFDMA systems[J].IEEE Transactions on Communications,2014,63(2):416-430.

[16] Ma G,Zhou Z,Bai J.Energy-efficient joint power allocation and channelselection for D2D communications[C]∥International Conference on Mobile Multimedia Communications,2015.

[17] Nickalls R W D.A new approach to solving the cubic:Cardan’s solution revealed[J].Mathematical Gazette,1993,77(480):354-359.

[18] Kim T,Dong M.An iterative hungarian method to joint relay selection and resource allocation for D2D communications[J].IEEE Wireless Communication Letters,2014,3(6):625-628.