基于支持向量机的滤波器设计与硬件实现*

计前程， 罗小华

(浙江大学 电气工程学院，浙江 杭州 310007)

0 引 言

滤波器是可执行信号处理功能的电子组件。数字滤波器系统包含对输入信号进行采样的模/数转换器，微处理器和一些外围组件，有时使用现场可编程门阵列(field programmable gate array,FPGA)或专用集成电路(application specific integrated circuit,ASIC)代替通用微处理器用于加速滤波操作[1]。

传统的有限脉冲响应(finite impulse response,FIR)滤波器有2种设计方法，窗函数法和频率采样法，存在通阻带边界的频率与波动不易控制等缺陷。自机器学习理论出现后，将神经网络等算法应用到FIR滤波器设计[2]中，取得了良好的效果，同时针对神经网络设计的FIR滤波器进行了硬件实现[3]。此外，开始使用支持向量机(support vector machine,SVM)设计FIR滤波器[4]。

本文使用SVM设计FIR滤波器，并根据FIR滤波器的情况针对SVM进行优化，改进了部分算法。在此基础上，提出了一种基于SVM的FIR滤波器的嵌入式系统。软件实现FIR滤波器的训练部分，硬件实现FIR滤波器的测试部分。滤波器性能良好，满足了基本要求。

1 滤波器结构理论

FIR滤波器属于线性系统。对于N阶因果离散时间FIR滤波器，输出序列的每个值为最近的输入值的加权和

(1)

式中x(n)为输入信号；y(n)为输出信号；N为滤波器阶数；hi为滤波器系数。

FIR滤波器的传递函数可由其冲激响应的z变换获得

(2)

可以得到FIR滤波器的频率响应

(3)

在设计FIR滤波器时，保证h(n)的对称可保证滤波器的相位特性，保证h(n)的大小可保证滤波器的幅值特性。

2 使用SVM设计线性滤波器

2.1 SVM

对于FIR滤波器，其输出可视作二分类问题，可使用SVM[5]作为分类器。

2.2 设计步骤

改写式(1)为向量形式，滤波器系数hi组成一个向量，输入信号x(n)组成另一向量，有

(4)

式(4)为一阶多维线性函数，与线性SVM的决策边界函数非常相似，可以经过简单的变换达到形式上的一致。由于滤波器的输出信号的范围大致在0～1之间，输出结果偏近1的信号为通过信号，输出结果接近0的信号为阻隔信号，可以通过数学方法，引入一个参数α，放大输出信号α倍并减去0.5α，使得y的值标准化，即令

(5)

此时，Y的取值范围大致在-1～+1之间，输出结果偏近+1的信号为通过信号，输出结果接近-1的信号为阻隔信号。考虑截止频率等因素，可以调整放大倍数。此时，式(5)可以看作一个决策边界函数。令

w=α×[h0h1…hN]

(6)

x=[x(n)x(n-1)…x(n-N)]T

(7)

变换后的滤波器函数为

(8)

考虑到训练样本可能存在错误，以及样本在决策空间中的距离可能很接近，引入松弛变量ξ和惩罚参数C。目标函数变为

(9)

由松弛变量的定义可知，松弛变量的取值为

(10)

式中yi实际滤波计算结果经变换后的值;y+,y-为目标结果，值分别为+1,-1。

将滤波器的约束条件施加在目标函数上，获得新的拉格朗日目标函数，该函数为

(11)

对Lp求偏导可获得约束条件。将约束条件施加在拉格朗日目标函数上，可以获得拉格朗日对偶函数。约束条件和拉格朗日对偶函数组成了针对拉格朗日乘子λi、滤波器的系数w和决策边界偏移量b的二次规划方程组

(12)

对式(12)求解，可以得到一组可行的拉格朗日乘子。将其代入到式(13)～式(15)中，即可求得滤波器的参数

(13)

(14)

(15)

2.3 使用核函数

引入核技术解决高维问题:设引入的核为k(xi,xj)，代入二次规划方程组后，可解得一组拉格朗日乘子和参数b。核函数有多种，其中,径向基函数(radial basis function,RBF)具有较宽收敛域[6]，使用广泛，因此,本文采用RBF核函数。计算如下

(16)

(17)

式中yi为支持向量xi标准化后的输出值;yz为测试向量z在标准化环境下的输出值;yreally为测试向量z在实际情况下应得的输出值。

2.4 参数优化

利用SVM训练16阶II型低通FIR滤波器。在[0,π]间平均取61组数据作为测试样本。

1)求取最少可用的训练集样本数

分别采用2,5,8,11,16,25,40组训练样本进行实验，σ=5，C=10。图1(a)为不同训练样本下的准确率。随着训练样本数的增加，滤波器模型的准确率不断提升。在训练组数达到16组后，准确率变化平缓。考虑硬件设计成本和滤波器准确率等，滤波器模型训练样本选取16组。

2)求取最合适的C值

采用8组C值进行实验，训练样本数为16，σ=5。图1(b)为得到的不同C值下的准确率。随着C值的增加，滤波器的准确率不断提升，但当C值达到一定值之后，滤波器准确率不再变化。可将SVM中的C值设为10。

3)求取最合适的σ值

采用8组σ值对滤波器进行实验，训练样本数为16，C=10。图1(c)为得到的不同σ值下的准确率。可以观察到，当RBF核σ值为20时，滤波器准确率最高。

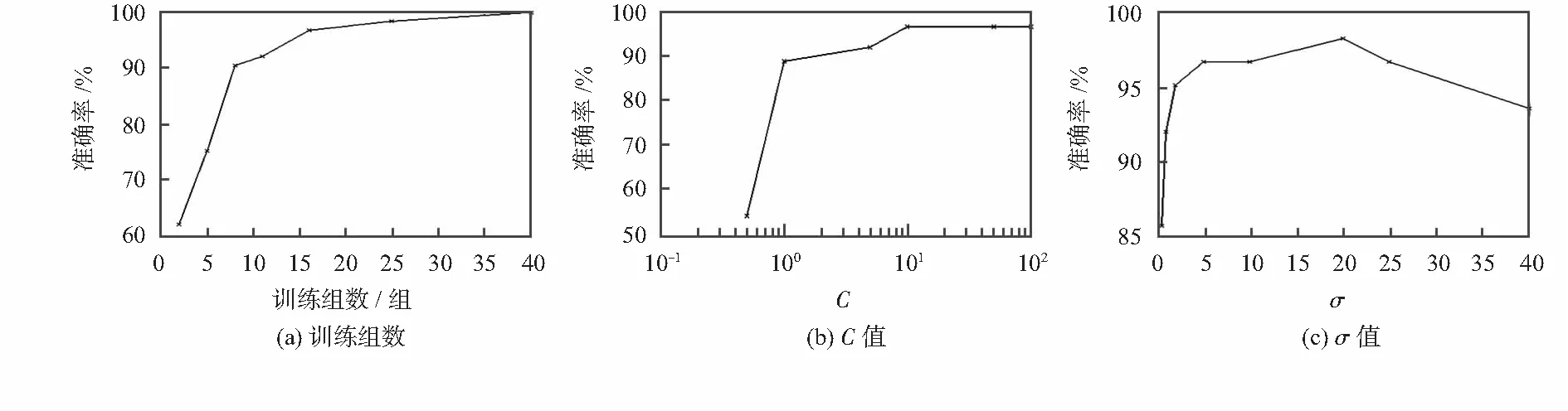
图1 各参数与准确率关系

3 滤波器嵌入式系统设计

3.1 整体系统设计

在Xilinx平台上完成关于基于SVM的FIR 的嵌入式系统设计。权衡设计成本和运算速度，FIR滤波器系统分为硬件和软件2个部分。软件主要实现SVM训练部分和测试部分中的运算框架，而硬件实现SVM中的核运算以乘加运算。图2为基于SVM的FIR 嵌入式系统的整体设计框图。本文通过软处理器核MicroBlaze完成了软件与硬件的连结。

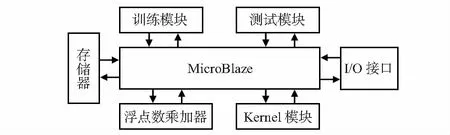
图2 嵌入式系统整体框图

3.2 硬件部分实现

硬件部分实现FIR滤波器系统中频繁使用的部分，浮点数乘加器和核函数模块。整个硬件模块如图3所示。

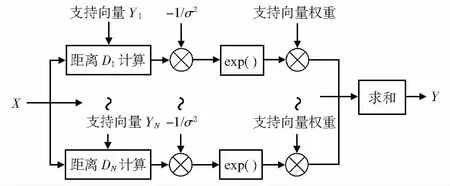
图3 硬件模块整体框图

浮点数乘加器完成使软件程序得到的权值与核函数模块相乘，并将所得到的N个积相加的工作，最终得到一个标准化的y值。核函数模块实现RBF核函数运算，其中包括距离求和运算、乘法运算,以及指数运算。本文指数运算调用CORDIC核[7]。

3.2.1 优化距离求和运算

(18)

在FPGA中，乘法运算会消耗较多的资源和时间，不利于模块内部的并行加速。因此，需简化距离计算公式来优化算法。本文设计的为一维滤波器，可以采用曼哈顿距离公式[8]替代欧几里得距离公式，即

(19)

设计曼哈顿距离计算的电路，如图4所示。曼哈顿距离计算电路由2个加法器、1个比较器和1个选择器组成，实现求取距离差绝对值的功能。

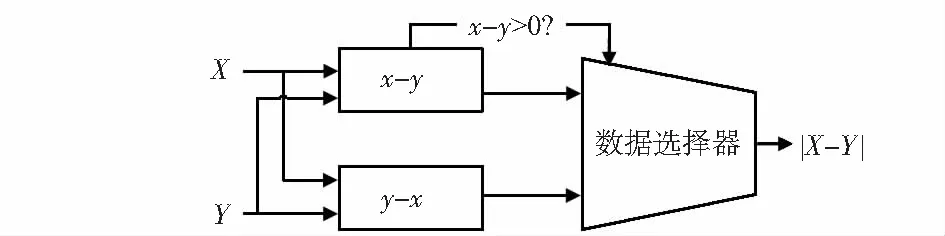
图4 曼哈顿距离计算电路

表1中，在使用流水线情况下，对于RBF核函数，使用欧几里得距离为137个时钟周期，使用曼哈顿距离为133个时钟周期，后者相比前者加速大约3 %。在乘法器的使用量上，后者较前者减少了2/3。由于使用曼哈顿距离会调用较多的加减器、比较器和选择器，会使用较多的查找表(look up table,LUT)，因此，LUT的使用量增长与此有关。

表1 硬件使用对比

3.2.2 向量分割

对于一个多维向量，其在输入时会消耗较多的端口，算法在硬件上的读写会被限制。可以将较长的向量分割成为多个小数组，提高端口的使用效率。向量分割时，寄存端口可以分时段地载入或载出数据，可以缩短启动间隔的时间，从而加速流水线。此外，分割后的向量变为多组小数组，在单元运算内部可采用并行计算，以减少单元运算的时间。

3.3 软件部分实现

3.3.1 序列最小优化算法

序列最小优化(sequence minimum optimization,SMO)算法[9]是一种用于解决SVM训练过程中二次规划问题的算法。SMO算法是一个迭代优化算法，其时间复杂度为O(n3)。运算步骤如下：

1)初始化向量的权重λi，权重取随机数，计算此时的偏移值b;

2)初始化每一项的误差Ei;

3)选取两个向量，作为要调整的点;

9)判断是否达到终止条件，如果是，则算法结束；否则，开始执行步骤(3)。

(20)

3.3.2 测试运算

1)初始化，获取拉格朗日乘子，支持向量；

2)计算拉格朗日乘子λi与yi的积；

3)计算关于支持向量xi的核函数；

4)将步骤(2)与步骤(3)的结果相乘；

5)求取和值获得主值w；

6)将w与偏移量b相加得到最终结果。

4 设计实例

最终优化后的SVM滤波器系统工作于100 MHz。系统使用开发板xc7z020clg484。表2中列出了硬件模块在开发板上的资源使用情况。其中，触发器FF使用了4 %，LUT使用了15 %，DSP48被调用了17 %，BRAM的使用率达到了9 %。单次计算并判定测试向量的时间约为3 500 ns。

表2 系统硬件资源使用

图5(a)为16阶II型低通FIR滤波器的在窗函数法下得到的幅频响应，图5(b)为在SVM设计下得到的幅频响应。SVM设计的FIR滤波器在通带和阻带范围内无过冲，边界控制精确。在[0,π]间平均取61组数据作为测试样本，SVM设计的FIR滤波器准确率可达到98.41 %。

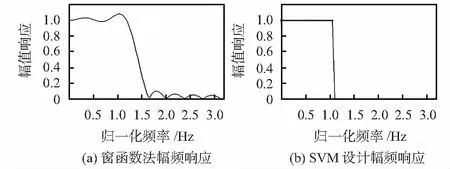
图5 不同设计方法下的幅频响应

5 结 论

基于SVM设计的FIR滤波器在通带和阻带范围内无过冲，边界控制精确。避免了传统滤波器设计方法中矩阵求逆时带来的大量计算，同时也避免了神经网络设计滤波器时需要较多的训练数据，加快了计算速度。本文设计的嵌入式滤波器系统，训练部分用软件实现，测试部分用硬件实现，可以实现资源与速度的平衡。从最终的幅频响应可以观察到，由SVM设计的FIR滤波器的幅频特性可以逼近理性滤波器，较传统方法具有优势。

[1] 刘 鑫,孙大军,滕婷婷,等.一种基于二阶锥规划的浮点分数时延滤波器[J].传感器与微系统,2014,33(12):101-104.

[2] Singh M A,Thakare V B V.Artificial neural network use for design low pass FIR filter a comparison[J].International Journal of Electronics and Electrical Engineering,2015,3(3):216-219.

[3] Kuldeep S Rawat,Massiha G H.Hardware implementation of FIR neural network for applications in time series data predic-tion[J].Indonesian Journal of Electrical Engineering,2015,14(1):130-139.

[4] 孙丰阔,席 斌.基于支持向量回归(SVR)的线性相位FIR滤波器设计[J].福州大学学报,2008,36(1):143-145.

[5] 陈中杰,蒋 刚,蔡 勇.基于SVM一对一多分类算法的二次细分法研究[J].传感器与微系统,2013,32(4):44-47.

[6] Mahnaz Mohammadi,Nitin Satpute,Rohit Ronge,et al.A flexible scalable hardware architecture for radial basis function neural networks[C]∥2015 14th International Conference on Embedded Systems,IEEE,2015:505-510.

[7] Shradha Gupta,Sumeet Saurav,Sanjay Singh,et al.VLSI architecture of exponential block for non-linear SVM classifica-tion[C]∥2015 International Conference on Advances in Computing,Communications and Informatics,IEEE,2015:528-532.

[8] 王一木，潘 赟，龙彦辰，等.基于自组织映射的手写数字识别的并行实现[J].浙江大学学报，2014,48(4):742-747.

[9] Naveenkumar M,Vadivel A.3D projected PCA based DMMfeature fusing with SMO-SVM for human action recognition[C]∥India Twelfth International Conference on Data Mining and Warehousing(ICDMW),Bangalore,India,2016:759-763.