轨交车辆自动驾驶控制关键技术设计

李海威， 赵 霞， 刘 循， 张琼燕

(1.上海交通大学 自动化系，上海 200241； 2.上海申通地铁股份有限公司，上海 200233)

0 引 言

随着城市的迅速发展及城市人口的大幅增加，建设高效的城市轨道交通系统已经成为解决城市交通拥挤问题的重要解决方法。然而，由于运行线路路况，包括车辆状况、线路、运量、站点情况、运行时刻要求等因素的影响，人工驾驶已难以应对越来越高的车辆运行要求。如何在保证列车运行的安全性、准时性的情况下，提高平稳性(包括舒适性)和降低能耗，是当前列车自动运行系统(automatic train operation system，ATO)研究的关键。这是一个涉及多变量自适应、多传感器融合的实时控制系统优化问题[1～9]。

本文根据上述要求开展了控制方法的研究，给出了一种高效、通用的实时控制算法,包括车辆自动运行基本控制参数定义、自适应控制模型构建、相关参数的界定等，以及对控制算法的验证。

1 与控制相关的参数

对于列车控制系统，输出为列车牵引率(制动率)a，控制目标是列车速度v，其中还包括基于舒适性的速度曲线、运行时间控制要求等。与牵引率和速度有关的相关参数包括：

1)土建状况：包括轨道坡度、弯道、隧道、站点限制等，对整个运行控制起到干扰作用；

2)车辆参数：包括车辆牵引力、运行阻力，随速度变化而产生变化;

3)乘客数量：重要的影响因素之一，其质量最终体现在惯量和摩擦力上。

列车控制系统对一些重要的参数，特别是涉及安全的要素配置了相应的传感器，包括承载重量、列车运行速度、加速度、站点位置传感器等。参数的实时获取，对于整个运行控制至关重要。此外，其采样频率和处理速度，也对控制精度产生影响。

2 相关参数界定

对于列车运行控制，动力参数是主要的输入，除了受控的牵引力外，还有不受人力操纵的外力，按其产生的原因，可分为基本阻力和附加阻力。附加阻力主要考虑坡道阻力、曲线阻力、隧道空气阻力等。牵引力为已知的，运行阻力为变化的，其加速度aw(m/s2)可以表示为

aw=aw0+awi+awr+aws

(1)

式中aw0为基本阻力加速度(包括由乘客质量变化造成的摩擦力影响)；awi为坡道阻力加速度；awr为轨道曲线阻力加速度；aws为隧道阻力加速度。

考虑到乘坐舒适性的要求，在实际控制中，对于加速度的变化速度有着一定的限制，即需对列车运行控制系统每个采样周期内的加/减速度变化率(冲击极限)进行限制。冲击极限的计算公式为

(2)

式中j为当前工况的冲击极限;ai为当前采样周期的加速度;awi为当前采样周期的列车运行阻力加速度;tsample为列车运行控制系统的采样周期。

3 列车控制模型建立

整个车辆的运行控制实际基于运动学、动力学分析和传感器的实时检测信息。根据速度、加速度、位置之间的关系，可以得到基本参数模型

ai+1=awi+1+(ai-awi)

(3)

vi+1=vi+(ai-awi)tsample

(4)

(5)

式中ai,vi分别为当前采样周期的列车加速度和速度;ai+1,vi+1分别为下一采样周期的列车加速度和速度;si+1为当前采样周期至下一采样周期的列车位移。

由于受到车辆牵引力的限制，加速度的边界条件为

ai∈[amin,amax]

(6)

ai≤maxa(vi)

(7)

式中 maxa(vi)为当前速度下列车所能提供的最大加速度。基于乘坐舒适性要求，冲击极限的边界限制条件为

(8)

式中jmax为列车所允许的最大冲击极限。

此外，由于列车在实际运行中存在着加减速过程，驱动电机特性的影响同样不可忽略，即此时电机会经过至少t0秒的惰行时间，需在控制中统一考虑。

式(3)～式(8)构成了完整的列车运行控制模型。

4 控制算法优化设计

考虑到ATO系统的多参数动态变化和稳定的控制输出要求，以比例—积分—微分(proportion integration differentiation,PID)控制器为基础，结合参数界定、控制预测算法的融入等方法，以解决由于复杂工况造成的控制扰动问题，实现安全、舒适、准时的全自动驾驶功能。

4.1 PID控制方程建立

从车辆速度v和列车牵引率(制动率)a的关系看，当速度与目标速度接近时，将目标加速度引入偏差，会极大地优化超调效果，为了达到更好的控制效果，选取了偏差量为速度偏差与加速度偏差之和的控制策略。相比仅采用速度作为偏差的方式，改进方法在交接段能够减少切换次数，从而使过渡更加平稳，同时也有利于延长设备寿命以及提升用户舒适度。

令PID控制器的参考速度为vin，实际速度为vout，参考加速度为ain，实际加速度为aout，则偏差量

e=vin-vout+ain-aout

(9)

PID控制器的差分方程为

u(k)=Kp(e(k)-e(k-1))+KIe(k)+KD(e(k)-

2e(k-1)+e(k-2))

(10)

4.2 控制器工作模式划分

为了使车辆运行中各阶段控制效果更好，交接更为平稳，对控制器的工作模式进行了专门的设置，包括:巡航模式(对应参考线巡航工况)、制动模式(对应参考线制动工况)和全牵引模式(实际速度与目标速度误差较大时采用全牵引工作模式，即施加条件所允许的最大加速度)。

本文参考线基于土建信息推算，参考线中仅有速度与位置的对应信息，但其所对应的加速度变化并未受到冲击极限的限制，同时参考线中无牵引工况。

4.3 工作模式转换标记点设置

运行控制器读取ATO全速运行参考线可以准确地读出工况转换的标记点。但由于参考线不受冲击极限的限制，而控制器的输出受到冲击极限的限制，因此，有一定的响应延迟，若完全按照参考线的标记点来切换工况，必然会产生较大的超调，并有可能会引发列车运行中的紧急制动。为有效地解决工况转换导致的超调问题，在工况转换时需要提前去除牵引(切除制动)，本文提出了采用预测方法来解决由冲击极限产生的延迟问题。

在确保与参考线有更好的贴合及避免过大超调的前提下，通过对工况转化标记点前移的方式来实现该目的。方法既能最大程度地贴合需求，又能极大地提升计算效率，为动态计算提供了更好的效率保障。

控制器的工作模式的合理划分以及相互间转换标记点的合理结合，可有效解决各工作模式交接段的超调问题。

工况转换点的具体处理方式如下

snew(n)=spoint(n)-tnvpoint(n)

(11)

式中snew(n)为标记点新的位置;spoint(n)为从参考线读取的工况转换点位置;tn为该点所对应的标记点前移时间常数;vpoint(n)为从参考线读取的工况转换点的速度。

4.4 控制器工作流程

控制器的完整工作流程如图1所示，其中初始化包括读取参考线、读取车辆参数(来自传感器)、读取工况转换标记点等功能。

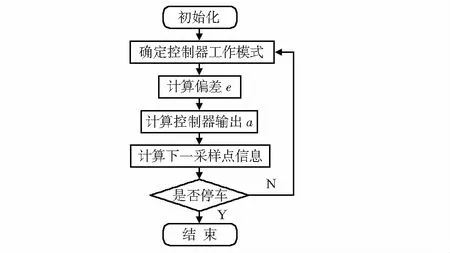
图1 控制器工作流程

4.5 控制系统仿真分析

为验证所设计控制模型的效果，进行了基于MATLAB的仿真分析。以上海轨道交通某站区间为参考线的仿真结果如图2所示。

图2 上海轨道交通某站区间仿真结果

图中1为参考线、2为列车闭环、3为控制器工作模式线、4为控制器输出线、仿真结果显示：全站运行过程中最大超调约0.1 m/s(要求不超过0.5 km/h)，旅行时间为90.45 s，停站精度为6 cm(要求不超过25 cm)，满足要求。该站区间的仿真所需时间约5 s，远低于该站的旅行时间，满足动态计算的要求。

5 控制系统中参数自适应设计

5.1 自适应控制需求分析

本文控制系统中，工况转换标记点前移量数值是一个重要的参数指标，该数值会直接影响超调量的大小，而此参数在控制系统运行通常使用经验参数先进行赋值，然后通过自适应调整并应用于后续的控制中。

5.2 参数自适应方法设计

1)评价标准设定

最大超调是控制器的核心评价指标，特别是过大的超调会导致列车运行过程中触发紧急制动。同时，能耗、旅行时间、停站精度也作评价指标进行综合评价。本文所选取的参考线为全速运行参考线，因此,未考虑能耗因素。综合各类指标有

U=U1+U2+U3+U4

(12)

式中U1为最大超调指标;U2为能耗指标;U3为旅行时间指标;U4为停站精度指标。

2)参数自适应实现方法

控制器首先会以默认参数进行计算，得到初步结果。若初步结果不满足要求，则通过改变控制器相应参数(可改变的参数包括标记点前移量、偏差计算的加权比例)，以一定步长逐步改变，直至满足评价要求。

5.3 基于参数自适应的仿真分析

为验证相关研究结果，以上海轨道交通某站为参考线进行了基于MATLAB的仿真分析。图3为仿真结果，该测试分析中选取的初始参数并不合理(标记点前移量过小而导致超调)，通过自适应逐步增大标记点前移量，可以看到自适应的效果。图中，1为参考线、2为列车闭环曲线、3为控制器工作模式线、4为控制器输出线。

仿真分析中仅选取最大超调作为评价标准，对标记点的前移量进行自学习。从此图中可以看出：该默认参数无法满足要求，在工况转换时超调过大，超调约为0.9 m/s，若按此运行必然触发紧急制动，不满足要求，经过系统参数自整定功能后，可以得到图2中的结果，满足要求。

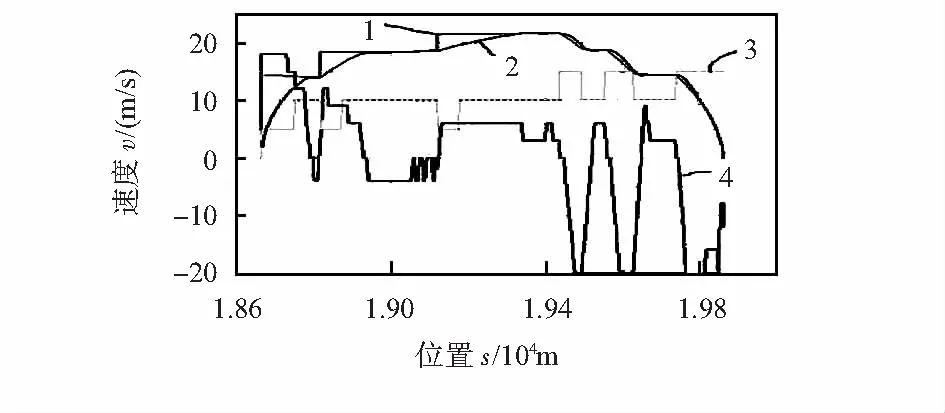
图3 上海轨道交通某站区间仿真结果(默认参数不恰当时)

6 结 论

针对轨交列车复杂工况，提出了一种基于多传感融合，多参数优化和参数自适应相结合的自动驾驶系统控制方法，并选用了实际线路数据，进行了仿真分析，验证了方法的可行性。目前，方法已在上海轨道交通线路中进行实际运行测试，效果良好。

所述的研究成果，为后续ATO自动驾驶控制器的多等级运行曲线及节能曲线的开发提供了良好的基础和可行的技术思路。

[1] 周翊民.城市轨道交通的发展趋势及其动因分析[J].城市轨道交通研究，2001(2):1-4.

[2] 余吉文.基于模糊预测控制的列车自动驾驶仿真研究[D].上海:上海交通大学，2013:2.

[3] 贾利民.智能多目标优化控制及其应用[J].信息与控制，1992，21(1):13-20.

[4] 李子钧.基于模糊自适应PID控制的列车自动驾驶系统的研究[D].北京:北京交通大学，2010:12.

[5] Oshima H,Yasunobu S,Sekino S.Automatic train operation system based on predictive fuzzy control[C]∥Proceedings of the International Workshop on Artificial Intelligence for Industrial Applications,Tokyo:1988:485-489.

[6] Nash A,Weidmann U,Bollinger S.et al.Increasing schedule reliability on Zurich’s S-Bahn through computer analysis and simulation[J].Transportation Research Record:Journal of the Transportation Research Board,2006,1955:16-25.

[7] Fernández-Rodríguez A,Fernández-Cardador A,Cucala A P,et al.Design of robust and energy-efficient ATO speed profiles of metropolitan lines considering train load variations and delays[J].IEEE Transactions on Intelligent Transportation Systems,2015,16(4):2061-2071.

[8] 刘海东，毛保华，丁 勇,等.列车自动驾驶仿真系统算法及其实施研究[J].系统仿真学报，2005，17(3):577-580.

[9] 张 强.基于遗传算法的列车自动驾驶系统研究与实现[D].北京:北京交通大学，2008:5.