基于ANSYS Workbench的变压器铁芯—绕组振动仿真*

姚 敏， 赵振刚， 高丽慧， 郭丽君， 李英娜， 李 川

(昆明理工大学 信息工程与自动化学院，云南 昆明 650500)

0 引 言

随着电力系统容量的增大，电力变压器的可靠运行与电力系统的安全密切相关[1～5]。电力变压器铁芯—绕组故障已经成为导致变压器损坏的最主要原因，因此，需要对变压器铁芯—绕组进行仿真分析，选择振动最强点作为测点对变压器工作状态进行实时监测，及时排除故障，使变压器可以安全稳定工作[6～8]。

本文分析了变压器铁芯—绕组的结构，利用有限元分析软件ANSYS Workbench建立了变压器铁芯—绕组模型，从夹紧和松动2种状态对铁芯—绕组的模态特征进行了仿真分析，找出变压器铁芯—绕组振动最强幅值的分布位置，为变压器振动情况的最优测点位置选择提供了理论依据；对比夹紧状态下铁芯—绕组振动的幅频特征，得到铁芯—绕组在夹紧状态下振动的基准幅值，为变压器振动情况的阈值设定提供了理论依据。

1 35 kV油浸式变压器结构模型

选择云南通变电器有限公司制造的S13—12500/35型油浸式无励磁调压电力变压器，铁芯具有稳定性好，噪音低，抗短路能力强的优点，绕组导电性能好，负载损耗低，适用于高海拔地区。

仿真分析时：1)忽略变压器油，认为其对结构件间力无影响；2)认为变压器结构件之间的连接无间隙，完全贴合；3)变压器绕组内壁被绕组套筒完全固定在铁芯结构件上。为了方便后续分析中进行模型剖分，避免圆弧处剖分密度过大，将圆柱体结构的铁芯和绕组，近似绘制成多边形结构，选择前后左右均对称的12边形作为绕组和铁芯的剖切面。同时，尽量避免切边倒角的圆弧倒角。利用ANSYS Workbench完成变压器结构建模，铁芯—绕组—结构件的有限元结构模型如图1。

图1 铁芯—绕组—结构件模型

2 35 kV油浸式变压器磁力分析

实际中，变压器的铁芯和绕组受到电磁力的作用。求解铁芯—绕组系统的电磁力时，利用电磁力分析软件ANSOFT Maxwell对铁芯—绕组的有限元模型进行了离散步电磁力载荷的加载。其中，仿真停止时间选取0.02 s，仿真步长选取0.000 1 s，得到变压器电磁力云图,如图2。

图2 电磁力云图

将分析得到的电磁力数据导入到ANSYS Workbench中得到铁芯—绕组系统的电磁力分布如图3表明:变压器铁芯绕组上方的电磁力密度较大，铁芯—绕组中电磁力最大值达2.445 8×105N/m3。

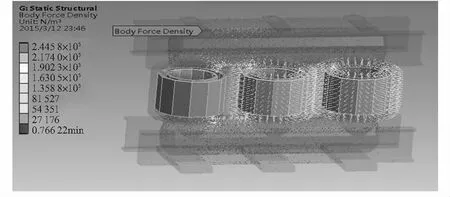
图3 电磁力分布

3 35 kV油浸式变压器铁芯—绕组振动模态分析

通过对变压器的振动仿真分析可以为变压器的设计及故障诊断提供理论依据，变压器的振动是各阶模态振型的复合，且随着阶次的递增，固有频率呈现递增的趋势。而载荷的固有频率较低，只需要分析与载荷频率接近的模态特征，因此，本文只研究铁芯—绕组前三阶的模态特征。

将上述电磁力数据导入ANSYS中，变压器中通入50 Hz正弦交流电，设置铁芯—绕组处于夹紧状态下的预紧力为26 MPa，其前三阶模态特征仿真如图4所示。设置铁芯—绕组处于松动状态下的预紧力为9 MPa，其前三阶模态特征仿真如图5所示。

图4 夹紧状态下铁芯—绕组的前三阶模态特征仿真

图5 松动状态下铁芯—绕组的前三阶模态特征仿真

对比分析图4、图5中相应模态的振型特征，得到压紧和松动状态下铁芯—绕组各阶振型特征如表1。

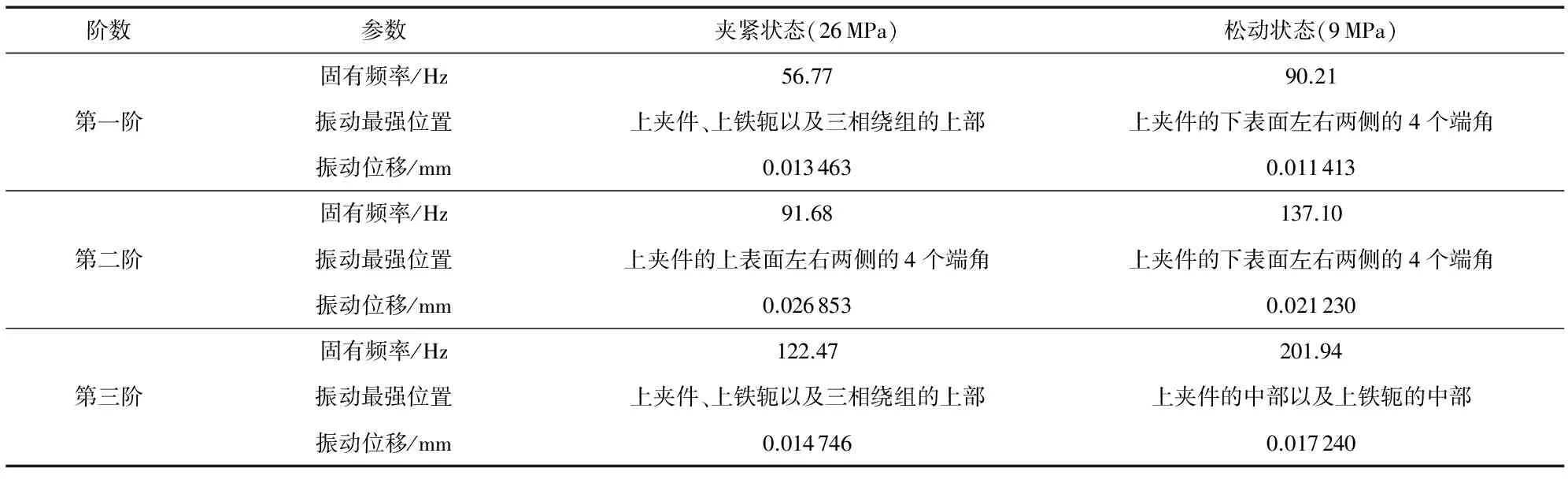
表1 压紧和松动状态下铁芯—绕组各阶振型特征

通过表1可知：铁芯绕组振动最强的位置主要分布在上夹件的中部和下表面左右两侧的4个端角、上铁轭的中部、三相绕组的上部。该振动强弱分布特征可以为变压器振动情况的实时监测选择最优测点位置提供理论依据。

4 35 kV油浸式变压器铁芯—绕组振动幅频响应分析

由变压器出厂参数知，该铁芯—绕组的正常预紧力范围在10～36 MPa。利用ANSYS分析其处于正常预紧力状态下的振动幅频响应情况。图6为铁芯—绕组在30，22 MPa的预紧力作用下的幅频响应情况。

图6 2种不同预紧力下的振动

根据图6幅频响应特征对比，该铁芯—绕组在正常预紧力下的主要响应频带在300 Hz以上，振幅频谱能量主要集中在100，300～350 Hz 附近。主要响应频带随着预紧力的减小，铁芯—绕组系统振动最大峰值呈现变小趋势，虽然在正常预紧力范围内，主要振动频率处的幅值存在波动，但波动较小，大约为0.003×10-7m。变压器出厂时，其结构的预紧力固定，正常运行情况下，其振动幅值为特定值，因此，可以将该情况下的振动幅值作为基准幅值，当变压器结构发生松动时，观察其振动幅值与基准幅值的差异度，从而判断预紧力是否发生变化。

5 结 论

为实时监测变压器的工作状态，及时排查故障问题，针对变压器铁芯—绕组结构进行仿真分析，获得其最强振动点分布情况，以选择最优点对变压器进行检测。根据变压器铁芯—绕组模型，在夹紧和松动2种状态下对铁芯—绕组的模态特征进行仿真分析，分析结果表明：铁芯—绕组振动最强的位置主要分布在上夹件的中部和下表面左右两侧的4个端角、上铁轭的中部、三相绕组的上部，可作为最佳测点；正常预紧力下的主要响应频带在 300 Hz以上，振幅频谱能量主要集中在100，300～350 Hz 附近，由此可确定阈值范围。

[1] 武新峰,雷勇军,李家文.基于有限元分析的复杂结构弹性振动传递函数建模[J].振动与冲击,2012,31(11):57-61,77.

[2] 王忠建.开关磁阻电机振动的有限元分析与控制研究[D].南京：河海大学,2002.

[3] 张式勤.双凸极电机的有限元分析及振动研究[D].杭州：浙江大学,2004.

[4] 刘 云.基于电子电力变压器的电力系统稳定性研究[D].武汉：华中科技大学,2013.

[5] 徐 志,杨永明,李 罗,等.变压器绕组状态的振动在线监测[J].传感器与微系统,2010,29(12):128-130，144.

[6] 杨文睿,董鸿魁,于凤荣,等.基于振动法的变压器振动在线监测系统[J].传感器与微系统,2016,35(1):88-90，94.

[7] 王 恩,曹 敏,李 博,等.基于Matlab热路模型的变压器绕组温度场研究[J].传感器与微系统,2016,35(7):51-54.

[8] Nicola Lamberti.A piezoelectric motor using flexural vibration of a thin piezoelectric membrane[J].IEEE Transcation on Utrasonics,Erroelectrics，and Frequency Control，1998，45(1)：23-29.