基于MEMS惯性传感器的行人导航轨迹复现研究*

赵 慧， 王 斌， 阮 巍

(重庆邮电大学 光电工程学院，重庆 400065)

0 引 言

惯性导航系统(inertial navigation system,INS)可满足无线电信号传播困难的地方对精确导航的需求。行人惯性导航是一种通过微机电系统(micro-electro-mechanical system,MEMS)惯性传感器采集行人运动信息，并运用计算机进行导航解算，及时更新行人的行走方向、位置和速率等信息，从而为行人提供一种可视化导航信息的方法。最近几年，MEMS惯性导航高速发展，体积和功耗不断减小的同时成本也大幅降低，使得MEMS惯性器件成为行人导航的理想选择[1]。

目前,行人惯性导航应用主要有2种方法。一种是采用行人航位推算(pedestrian dead reckoning，PDR)方法，即通过加速度输出值来检测行走的步数、近似步长，磁场或陀螺仪判断航向，推算出行人的位置[2]。文献[3]采用传统惯导与零速检测结合，由于进行滤波优化，最终误差为8.2 %。文献[4]采用步长、步数、航向的方法，最大误差低于总行走距离的3.0 %，但定位精度很大程度上取决于方向角精度以及行人的步行习惯。文献[5]采用了互补滤波将数据融合得到轨迹，行走过程中方向会转变360°，造成较大误差，误差控制在6.3 %。文献[6]采用了粒子滤波算法融合室内地图，室内误差为3.0 %，但航向角不可观测，轨迹容易发生穿墙现象，导致轨迹漂移。文献[7]给出了较好的结果，但采用经验性的方法由于不能识别不同行人的步态变化，故当采用与以往不同的方式进行移动时算法失效。

另一种方法为传统的捷联式惯性导航，即将惯性测量单元(intertial measurement unit,IMU)固定在鞋上，通过处理IMU输出的加速率、角速率值，预测行人的姿态信息和位置[9],此方法不会因为人的改变而失效。因此,本文采用捷联式方法进行实验。将惯性传感器固定于脚面，得到滤波后的加速率和角速率值，实现方位角的修正，从而提高行人导航的定位精度，行走一圈平均误差控制在3 %、行走多圈平均误差在5 %以内。

1 方案设计

为选取合适的惯性测量单元，需考虑多种因素，如重量、体积、采样率、成本及功耗等。本文选取的惯性传感器模块为一集成三轴加速度计与三轴陀螺仪的MPU6050和一三轴数字罗盘HMC5883L。

硬件系统以开源电子原型平台ARDUINO UNO为核心，软件环境为MATLAB。方案设计流程如图1所示，通过三轴加速度计与三轴陀螺仪采集数据，一方面利用捷联式惯性计算，另一方面进行零速检测，满足零速修正(zero velocity update,ZUPT)条件时则触发卡尔曼滤波，与捷联式惯性计算融合，最终得到行人导航位置轨迹。

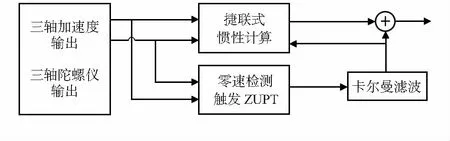
图1 方案设计流程

2 算法实现

为实现完整的行人惯性导航：1)对坐标进行转换，将载体坐标系转换到导航坐标系中，在导航坐标系得到姿态角；2)对经过滤波的加速率和角速率进行零速检测，通过改进的卡尔曼滤波处理，得到行人的惯性导航。

2.1 姿态角初步估计

行人行走是一种低速运动，因此忽略地球自转所带来的影响，只在空间内定义2种坐标系：导航坐标系(n系)和载体坐标系(b系)。

n系为当地水平坐标系，x轴指向北，y轴指向西，z轴与x,y轴满足右手定则指向天，即为北西天坐标系，行人行走的方向和速率均在系内推算。b系三轴与惯性测量单元(inertial measurement unit,IMU)固定，并随着载体的运动而变化，定义x轴为前向，y轴为左向，z轴与x,y轴成右手定则，原点O在IMU的重心，陀螺仪和加速度计的初始值均基于载体坐标系[9]。

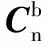
(1)

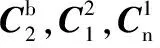
图2 载体—导航坐标转换

2.2 零速检测

零速检测指当行人行走脚落地过程或者行人静止状态下，束有INS的脚在落地期间，理论上,其角速率和加速率均为零。通过检测落脚瞬间，可以人为消除陀螺仪和加速度计输出值的累积误差。

为了精确判断零速度时刻，提高定位精度，本文采用三条件判断法，即三轴总加速度检测、三轴总加速度方差检测和三轴总角速度检测。以“1”表示零速度状态，即脚完全落地的状态。

2.2.1 三轴总加速度检测

当脚落地静止时，基本只受重力作用，此时三轴总加速度的幅值处于2个阈值之间

(2)

其中

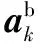
(3)

式中 |ak|为三轴总加速度;thamin,thamax为加速度区间阈值。

2.2.2 三轴总加速度方差检测

行人步行过程中，加速度剧烈变化，行人静止时刻，加速度变化平缓，此时三轴总加速度方差处于一个阈值如下

(4)

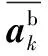
(5)

则

(6)

式中thσmax为加速度方差的阈值。

2.2.3 三轴总角速度检测

行人步行过程中，角速度剧烈变化，静止时刻，角速度几乎为零，此刻三轴总角速度幅值处于一个阈值范围内

(7)

(8)

式中thωmax为角速度阈值。

上述3个条件通过逻辑“与”(&)运算，即可得到最终落地点，即零速度的时刻

C=C1&C2&C3

(9)

3个判断条件中，设定结果为“1”时表示速度为零，即为脚全部落地时刻。图3为零速检测结果，前3行依次为总加速度检测结果C1、总加速度方差检测C2、总角速度检测C3，第四行为前三行进行逻辑“与”运算得到的结果C。

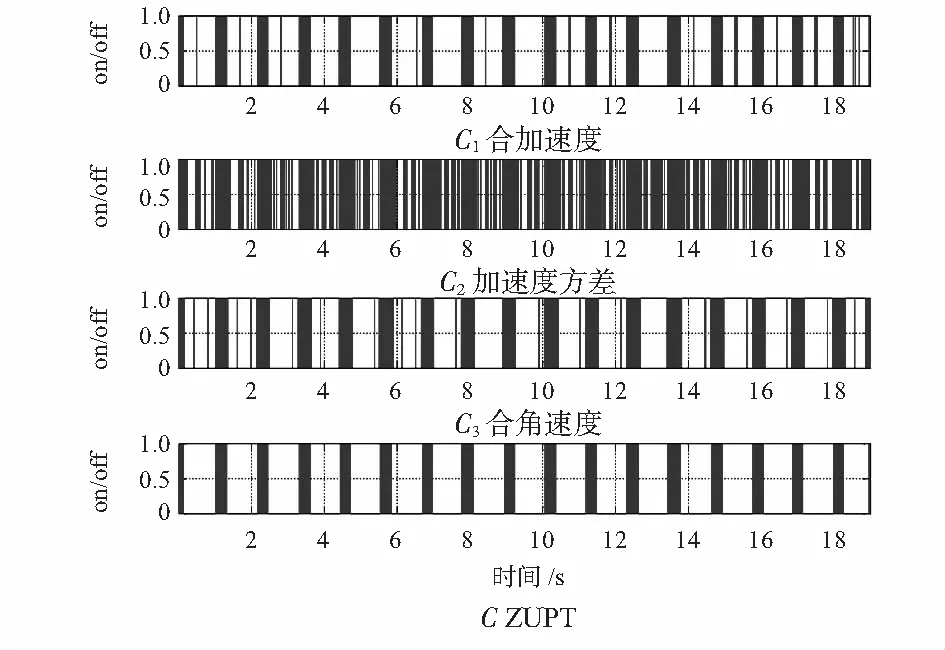
图3 零速检测结果

2.3 卡尔曼滤波优化算法

为了预测零速度时刻的误差，对于卡尔曼滤波，设置其在k时刻的15个状态向量状态∂xk=[∂γk∂vk∂φk∂ak∂wk]。其中,∂γk,∂vk,∂φk分别为位置、速度和姿态向量，而∂ak,∂wk分别为加速度和陀螺仪的漂移错误值[10]。

2.3.1 时间更新

通过加速度和角速度采样值进行导航解算，更新当前状态向量状态∂xk以及相应的四元数q，并根据结果计算卡尔曼滤波中的状态转移矩阵Fk、系统噪声增益矩阵Gk以及协方差矩阵P。

状态转移矩阵为

(10)

式中St为加速度的斜对称矩阵，矩阵元素依据转换成导航坐标系的加速度值创建；B1，B2则分别为加速度和陀螺仪的偏差相关常数。

(11)

(12)

2.3.2 测量更新

计算当前卡尔曼增益，并将速度信息作为系统速度误差的测量值，再根据状态估计更新方程对行人的速度、位置进行重新估计，同时计算系统的姿态矩阵，最终得到新的速度、位置和姿态角信息。

3 实验验证

为了验证设计的行人导航系统的可行性，在室外绕圆形路线，在室内绕矩形路线进行行走实验。

3.1 圆形路线测试

实际路线为绕直径为13.00 m的圆形，绕实际路径进行顺时针行走一圈得到结果如图4所示，测量的误差为2.8 %，实验行走的落脚点落在实际路线的外围，原因为左脚位于人体中心左侧，与实际情况相符，最终导航结果满足导航要求。

图4 圆形轨迹落脚点轨迹

3.2 方形路线测试

实际矩形路线为6.20 m×6.70 m，如图6中点划线所示。图5为仅用加速率和角速率直接累积得到的导航位置，误差结果很大。图6为经过修正得到的位置轨迹，误差主要产生在转弯处，测得误差为2.8 %，满足导航要求。图7为绕矩形方块行走3圈的轨迹，计算误差为4.2 %，产生误差的原因主要包括：磁力计的偏差、步行运动的抖动以及转弯时产生的偏差。

图5 矩形形状直接解算轨迹

图6 矩形形状单圈导航轨迹

图7 矩形形状3圈导航轨迹

3.3 对比结果

为了验证算法的准确性，将本文测量结果与其他文献结果进行比较，如表1所示。

表1 不同方法得到的轨迹对比 %

4 结 论

采用低精度的MEMS惯性器件，通过分析行人行走的步态特征，利用卡尔曼滤波算法和零速检测，实现了行人行走的轨迹复现。实验结果表明:一次行走路径圆形与矩形时测量误差均小于3 %，较好地满足了行人导航的需求。轨迹复现的过程中有一定延时，原因为行人按实际路径行走时传感器采集数据上传至MATLAB软件，MATLAB软件运算产生了延迟，如何减少延迟时间成为下一步的工作目标。

[1] Hazas M,Scott J,Krumm J.Location-aware computing comes of age[J].Computer,2004,37(2):95-97.

[2] Jimenez A R.Indoor pedestrian navigation using an INS and EKF framework for yaw drift reduction and a foot-mounted IMU[C]∥Positioning Navigation and Communication,2010.

[3] 万骏炜,曾庆化,陈磊江,等.行人惯性导航系统平台设计与实现[J].计算机应用与软件,2015,1(2):45-47.

[4] 李金凤,王庆辉,刘晓梅,等.基于MEMS惯性传感器的行人航位推算系统[J].传感器与微系统,2014,33(12):85-87.

[5] 肖永健,肖 力,孙志刚，等.基于步行者航位推算的井下人员辅助定位[J].太赫兹科学与电子信息学报,2013，6(4):583-587.

[6] 崔 潇,秦永元,周 琪,等.鞋式个人导航系统算法和试验研究[J].测控技术,2013,32(3):138-142.

[7] Renaudin V,Yalak O,Tomé P,et al.Indoor navigation of emergency agents[J].European Journal of Navigation,2007,5(3):52-58.

[8] Caruso J.Application of magneto resistive sensors in navigation systems[J].Sensors and Actuators,1997,1220(1):15-21.

[9] 秦永元.惯性导航[M].2版，北京:科学出版社,2006:5-8.

[10] 杨 辉.基于MEMS传感器的高精度行人导航算法研究[D].厦门：厦门大学,2014.