行人低成本惯导自适应零速探测

胡 鑫，陶贤露，朱 锋，张小红,2

（1. 武汉大学 测绘学院，武汉 430079；2. 地球空间信息技术协同创新中心，武汉 430079）

0 引言

全球卫星导航系统（global navigation satellite system, GNSS）芯片在智能手机、智能可穿戴设备中可以实现全覆盖，在室外良好观测条件下，可提供10 m左右精度的定位结果，通过辅助GNSS技术，可以缩短首次定位时间，利用差分GNSS技术，可以提高GNSS定位精度，能够基本满足室外定位需求。在室内，通过无线局域网、低功耗蓝牙、超宽带、地磁、室内地图等信息源定位，可以实现局部区域的米级定位。但上述室外内定位方法受到使用范围和成本的限制，在城市、峡谷、高架桥下等遮挡区域，卫星导航信号减弱，仅使用GNSS无法获取连续的定位结果；而蓝牙、超宽带、室内地图等室内定位技术，则依赖基础设施和数据库，仅能在部署了基础设备、采集了数据库的区域使用[1-3]。

随着传感器工艺水平迭代更新和性能提升，大众用户终端如智能手机和智能可穿戴设备搭载的低成本的传感器，具备了更高的精度和稳定性，可以利用其中的微机电系统（micro-electromachanical system, MEMS）惯性测量单元（inertial measurement units, IMU）进行行人航位推算（pedestrian dead reckoning, PDR）。PDR算法包括惯性导航系统和步长航向系统两类，惯性导航系统具有自主性强、动态性能好、导航信息全面且输出频率高等特点，可以获得高频率的位置、速度和姿态更新，更利于通过卡尔曼滤波与其他定位信息融合；步长航向系统通过计算行人每一步的位置变化，来进行水平位置更新[4]。以PDR定位结果为辅助信息，在室外与GNSS定位结果融合，可以优化室外GNSS遮挡环境下的定位结果；在室内与蓝牙、超宽带、地磁和室内地图融合，可提升室内定位精度；在室外GNSS信号中断、室内无无线定位设施时，PDR可以在一定时间内维持较高精度的定位结果；在室外、室内定位切换区域，由于GNSS信号遮挡，而室内定位信号又不能很好覆盖时，利用PDR可实现室内外连续、高精度定位切换[5-7]。但是用低成本的IMU进行机械编排，存在精度维持时间短的问题，由于高程和航向不可观测，高程和航向角长时间解算后，也会有明显的漂移。将传感器安装在行人足部，根据行人行走特征或其他传感器提供的观测信息，通过卡尔曼滤波进行观测更新，修正机械编排结果的误差。此外，在二次速度更新之间，可以构建航向自观测模型来约束航向漂移[8]。使用气压计、磁力计进行高程和航向时零速探测也很重要，例如进行航向角更新时，利用零速时加速度计3轴输出为重力分量的特点，只解算零速时刻的磁航向角，避免了高动态状况下提取重力分量误差大的问题，可提升磁航向角解算精度；零速间隔通常包含超过10个的连续零速状态历元，通过零速间隔内的磁航向角取中值的方法，可以提高磁航向角的可靠性。

零速探测效果决定了PDR解算和多源融合定位精度，一方面可以在机械编排过程中，通过速度、零角速度、零加速度约束抑制误差发散；另外一方面，在与其他传感器融合的过程中，通过解算零速间隔内的气压计高程和磁航向角并取中值，可以显著地提升高程和航向观测的精度和可靠性。因此，要减少将运动状态误判为零速的可能性，避免引入错误的高程、速度和航向观测；要提高将零速准确判断为零速的概率，确保能够及时进行观测更新，有效抑制误差的发散。现有的零速探测方法大多是基于检验统计量和固定阈值，当检验统计量小于阈值时，判断传感器处于静止状态，或通过多种零速探测方法组合，提高零速探测的可靠性[9-12]。通过分析不同行走状态下检验统计量的特征，本文提出1种通过窗口内检验统计量最小值和幅值计算自适应阈值的方法，阈值能够根据窗口内检验统计量的特征变化进行动态调整，通过幅值参数降低将动态时刻误判为零速的概率，通过最小值保证每一步都能探测到零速。利用本文的自适应阈值零速探测结果，进行零速更新和多传感器融合定位，旨在避免引入异常观测信息的同时，确保能够及时地进行观测更新，有效地抑制误差发散，显著地提升多传感器融合定位精度。

1 传感器信息及信号模型

1.1 传感器信息

本文的研究基于1款低成本MEMS模块，该模块集成了加速度计、陀螺仪、磁力计、气压计，设置数据输出频率为100 Hz时，加速度计零偏为0.1 m·s-2，陀螺零偏为0.05 (°)·s-1，传感器数据通过蓝牙实时传输至自研手机行人导航软件。模块零售价格百元左右，内置了MPU-9250和BMP-280模块，性能和成本与智能手机、平板电脑等大众用户智能终端接近，远低于当前被广泛用于足部PDR研究的Xsens MTi、Inertial Elements、ADIS等品牌产品[9-14]，可以更好地满足大众用户对低成本、便携的要求。

1.2 传感器信号模型

加速度计测量模型为

式中：If为加速度计测量值，单位为m ⋅s-2；f为真实比力，单位为m ⋅s-2；bf为加速度计零偏，单位为m ⋅s-2；S1为线性比例因子误差矩阵；S2为非线性比例因子误差矩阵；N为交轴耦合矩阵；δg为重力异常，单位为m ⋅s-2；εf为加速度计传感器噪声，单位为m ⋅s-2。

陀螺仪测量模型为

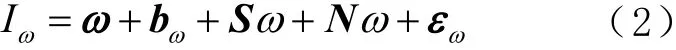
式中：Iω为测量值，单位为(° )⋅s-1；ω为真实角速度，单位为(° )⋅s-1；bω为陀螺零偏，单位为(° )⋅s-1；S为陀螺比例因子矩阵；εω为陀螺仪传感器噪声矢量，单位为(° )⋅s-1。

磁力计测量模型为

式中：Im为测量值，单位为μT；Cno为非正交阵，表示轴间耦合误差，由于通常情况下是1个小角度，对角线元素一般非常接近1；Csf为比例因子阵，来源于各轴的灵敏度不一致，对角矩阵上的每1个元素代表各轴的灵敏度；Csi为软磁误差矩阵；Cm为安装误差矩阵；m为真实磁场3轴分量，单位为μT；bH为硬磁误差；b zb为零偏，单位为μT，来源于磁力计各轴的常值偏差；mε为磁力传感器噪声[15]。

1.3 零速状态传感器信号特征

将传感器固定在行人足部，当安装传感器的脚落地处于静止状态时，传感器的速度为零且速度、位置和姿态不变，对应线性加速度和角度变化量、高程变化量的理想值为零。即静止状态时，如果不考虑传感器误差及环境干扰等因素，加速度计3轴输出为重力分量，3轴输出的模值等于重力，前后历元间变化量为零；陀螺仪3轴输出为零；磁力计3轴输出的历元间变化量为零。

受到零偏、比例因子等传感器误差的影响，静止时刻传感器输出特性并非如前所述。但加速度计和陀螺仪受环境影响相对较小，静态和动态时刻数据差异明显，适合用于零速检测。磁力计易受外界磁场环境干扰，静态情况下受到较多磁干扰时，磁力计输出变化较为剧烈，用磁力计数据进行零速探测易受磁干扰影响。气压计的实际采样率和分辨率较低，一方面无法准确探测零速时刻的具体时间，另一方面由于测量噪声较大，约为1.3 Pa，对应高程误差约为0.11 m，无法准确反映行人运动状态的变化。因此，使用加速度计和陀螺仪的原始输出进行零速探测更加稳健可靠，利用加速度计和陀螺仪输出进行零速探测时，传感器输出可表示为

当k时刻为零速时刻时，理想情况下加速度计和陀螺仪输出为

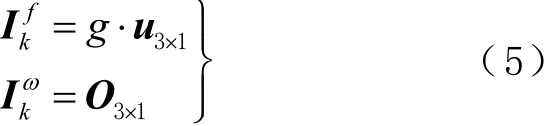
式中：g为当地重力；u3×1和O3×1为3×1列向量，且u3×1的模为1；O为矩阵元素为0的矩阵

2 零速探测方法

行人步行时，足部的运动分为静止和运动2种模式。给定一段观测值序列，通过该观测值序列进行零速探测。需要降低将运动状态误判为零速状态的概率，因为如果将运动状态判断为零速状态，将给导航系统引入较大的误差；需要提高准确判断零速的概率，因为每1个准确的零速状态历元都能对导航系统的误差进行修正，提高定位精度。基于此，将零速探测看成二元简单假设检验：H0为运动状态，H1为零速状态。零速探测的效果由将运动状态误判为零速的虚警概率PFA=Pr {H1|H0}和将零速状态准确判断为零速状态的探测概率PD=Pr {H1|H1}决定。为保证及时提供准确的零速修正信息，需要把虚警概率控制在一定范围内，并且让探测概率尽可能高。用奈曼-皮尔逊准则和极大似然法检验推导出检验统计量的计算方法[13]为

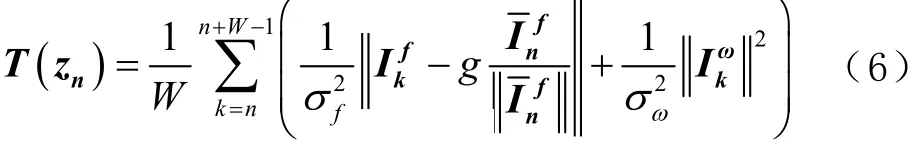
式中：W为零速探测窗口大小；zn是零速窗口内的传感器输出，分别为加速度计和陀螺仪的噪声方差；为零速探测窗口内加速度计输出各轴比力平均值矢量。

行人在不同的运动模式下，足部静止的特性不同。缓慢行走时，行人足部状态更接近完全静止状态；快速行走时，静止时刻足部状态没有缓慢行走时稳定；上楼梯时，行人抬脚高差大，落脚高差小；下楼梯时，行人抬脚高差小，落脚高差大。IMU的原始输出能够很好地反映出上述特性，具体表现在：随着行人行走速度变快，加速度计和陀螺仪输出幅值变大，解算的检验统计量T(zn)的幅值及窗口内的最小值也变大；上下楼梯过程中，陀螺仪输出幅值与平地行走状态有明显区别，陀螺输出右方向幅值上楼梯明显小于平地行走，平地行走明显小于下楼梯，相应的检验统计量T(zn)特征也有显著区别。

以行人不同速度绕1个直径18 m的圆行走4圈的数据为例，数据采样率为100 Hz，行人每1圈的平均速度从慢到快，加速度计、陀螺仪3轴输出和模值如图1、图2所示，检验统计量和水平速度如图3所示。

图1 加速度计原始输出及模值

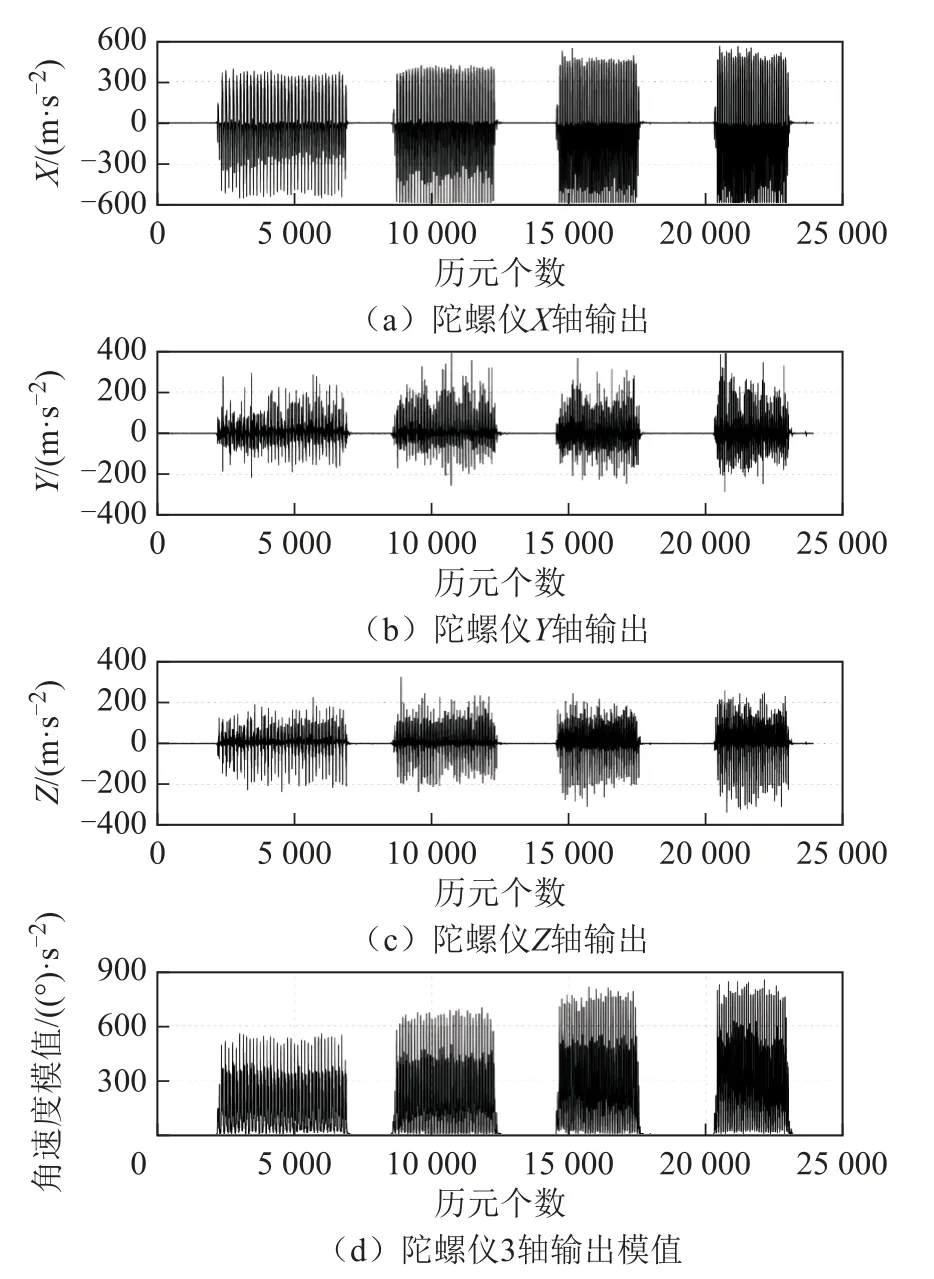
图2 陀螺仪原始输出及模值

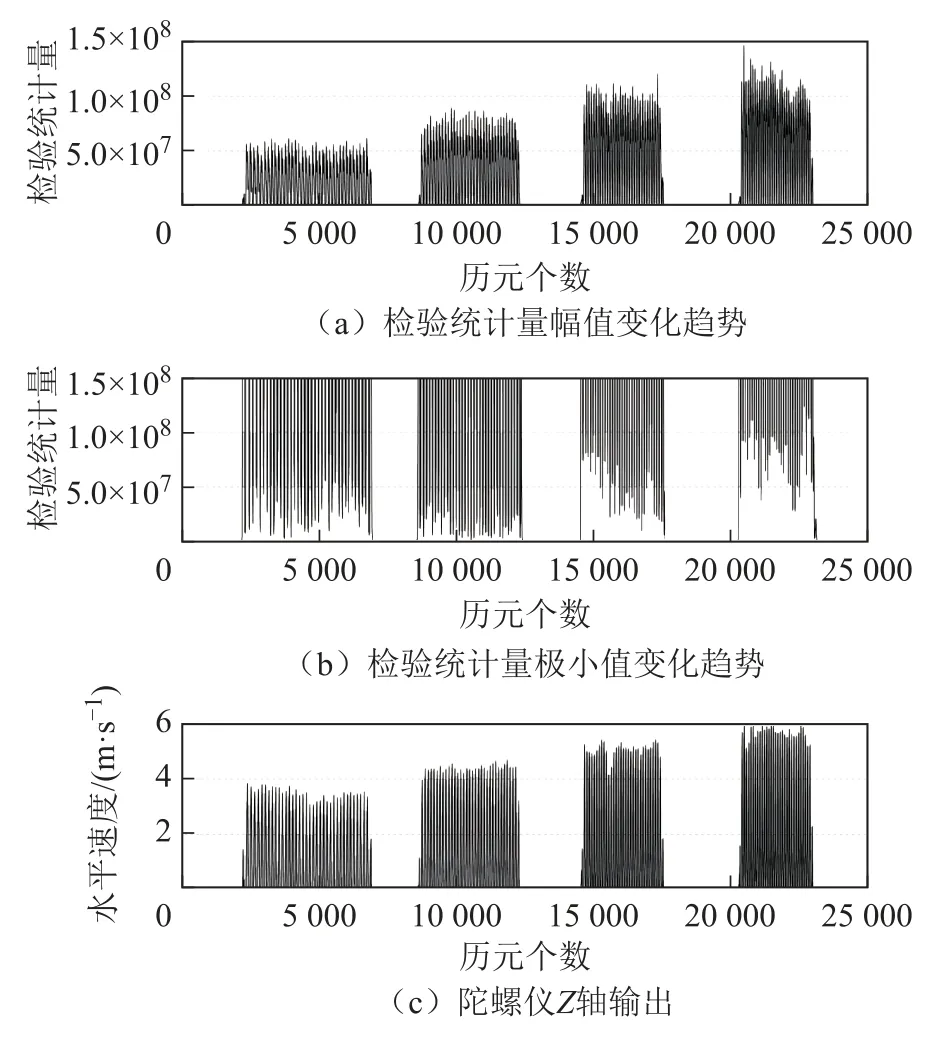
图3 检验统计量、水平速度

从图1至图3可以看出，加速度计、陀螺仪3轴输出和模值的幅值随着步行速度加快增大，检验统计量、检验统计量极小值也对步行速度敏感。如果设置阈值为 ×55 10，第1圈和第2圈能准确地探测出几乎所有的零速，但是第3圈和第4圈会有大量的零速状态不能准确地被探测出来。如果设置阈值大于 ×63 10，虽然能探测出第3圈和第4圈所有步数的零速间隔，但第1圈和第2圈探测出的零速间隔将会过长，将静止状态前后的运动状态也探测为静止状态，从而引入错误的速度观测信息。行人从站立状态到步行状态，以及从步行到站立状态时的运动速度很小，计算出的检验统计量也很小，用固定阈值很容易将该时段误判为零速状态，导致出发时刻就出现较大的姿态、速度误差。

还可以利用不同的检验统计量计算方法来改善零速探测效果，包括加速度移动方差（moving variance, MV）、加速度模值 （magnitude, MAG）、角速率能量（angular rate energy, ARE）等，或将这些方法综合利用，可以优化零速探测效果[13]。相关检验统计量计算方法为：

式中：TMV(zn)为加速度移动方差法计算的检验统 计 量；TMAG(zn)为 加 速 度 模值 法 计 算 的 检 验统计量；TARE(zn)为角速率能量法计算的检验统计量。

通过上述3种方法计算出的检验统计量极小值特征如图4所示。

图4 3种方法计算检验统计量的极小值

从图4中可以看出：不同方法计算的检验统计量，同一时刻的幅值、极小值不同，但窗口内的幅值和极小值均存在随速度变化的特性；因此通过检验统计量与固定阈值相结合进行零速探测，无法从根本上改善不同状态行走的零速探测问题。而通过姿态识别后设置不同的阈值组合，利用先验速度调整阈值的方法对行人速度不够敏感，在速度突变以及步行开始、结束时容易导致漏检或误判。

本文提出1种自适应阈值计算方法，取长度为W的窗口计算窗口内统计检验量T(zn)，自适应阈值计算方法为

式中：aλ为自适应阈值；min为取最小值；max为取最大值；q为幅值参数。

该方法基于窗口内检验统计量的幅值和最小值，计算得到的阈值能够很好地反映窗口内检验统计序列的特征，继而能够反映运动速度的变化。通过窗口内取最小值，可以保证每一步均能探测出零速状态，以便及时进行零速更新，保障零速更新效果。q可以在每一步都能探测出零速时刻的基础上，将更多的零速状态准确探测出来：q越大，每一步被探测为零速的时间间隔越长，q过大，则会将部分非零速状态判断为零速状态；q越小，运动状态被误判为零速状态的概率越小，q过小，则会导致部分零速状态漏判。在机械编排/零速修正解算过程中，如果将动态误判为零速状态，则会引入错误的速度观测信息，导致解算距离较真实距离更短；但是在每1步都能探测出零速状态的基础上，即便存在部分零速时刻被漏判，也保证能及时进行零速更新，且不会引入速度观测误差：因此须要在确保不出现将动态误判为静态的情况下，尽可能地提高将静态准确判断为静态的概率。经实验验证，q取值为0.01左右时，能够保证及时、足够地判断零速，且能有效地避免误判零速的情况。因此本文q取值为0.01。

3 自适应零速探测及零速修正结果

3.1 自适应零速探测结果

将绕直径18 m的圆，以不同速度走4圈的数据分解为4组1圈的数据，其中第1圈和第2圈的行走速度较慢，第3圈和第4圈的行走速度较快，4组数据对应的用时、平均水平速度、步数如表1所示。

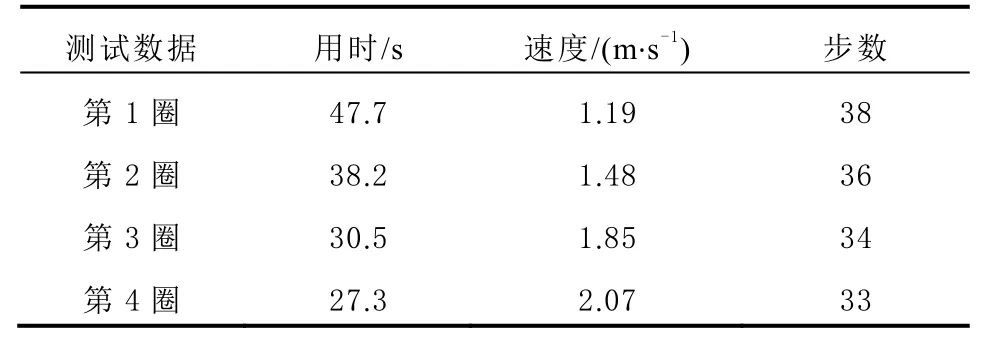
表1 四组测试数据信息

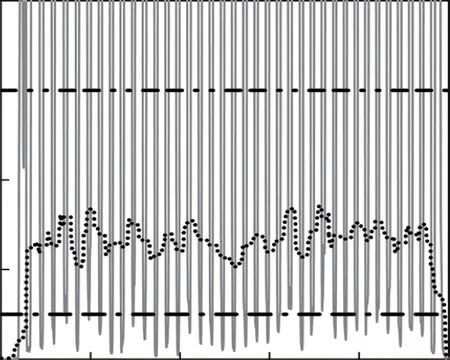
图5 第1圈检验统计量与不同阈值之间的关系

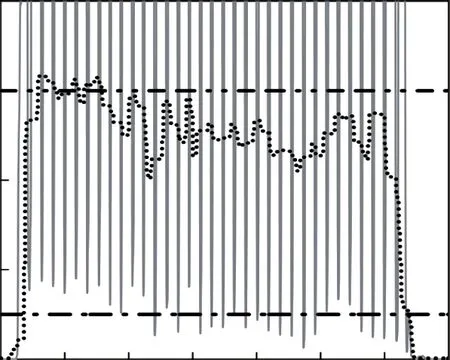
图7 第3圈检验统计量与不同阈值之间的关系

用自适应阈值aλ、固定阈值λ=×51 5 10、固定阈值λ=×62 3 10分别解算表1中的4组数据，对比零速探测结果和零速修正解算结果。4组数据的检验统计量、自适应阈值aλ、固定阈值1λ、固定阈值2λ的关系如图5至图8所示，对应的误检和漏检统计如表2、表3所示。

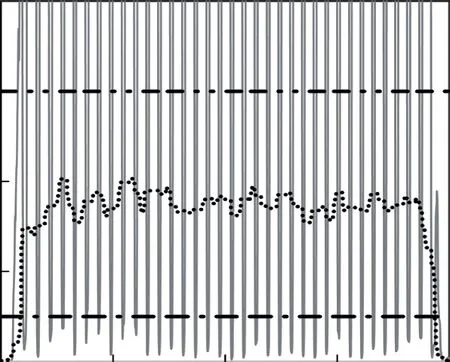
图6 第2圈检验统计量与不同阈值之间的关系

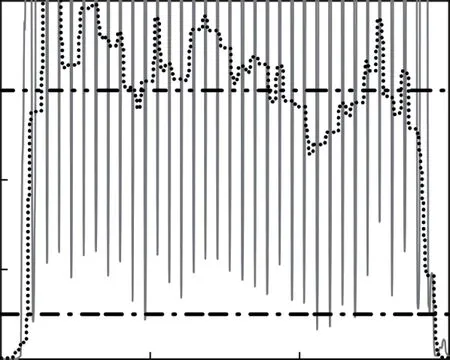
图8 第4圈检验统计量与不同阈值之间的关系

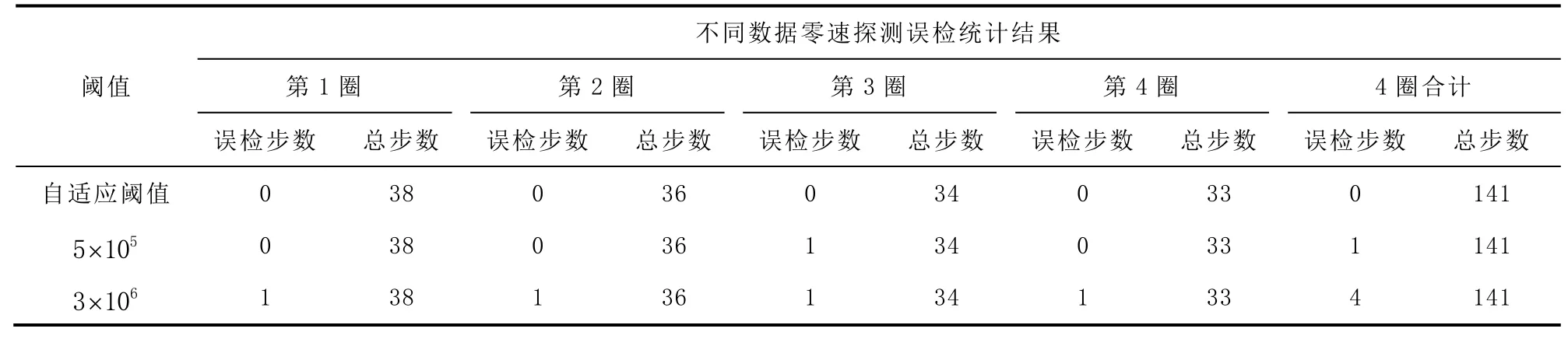
表2 不同零速探测阈值误检统计表

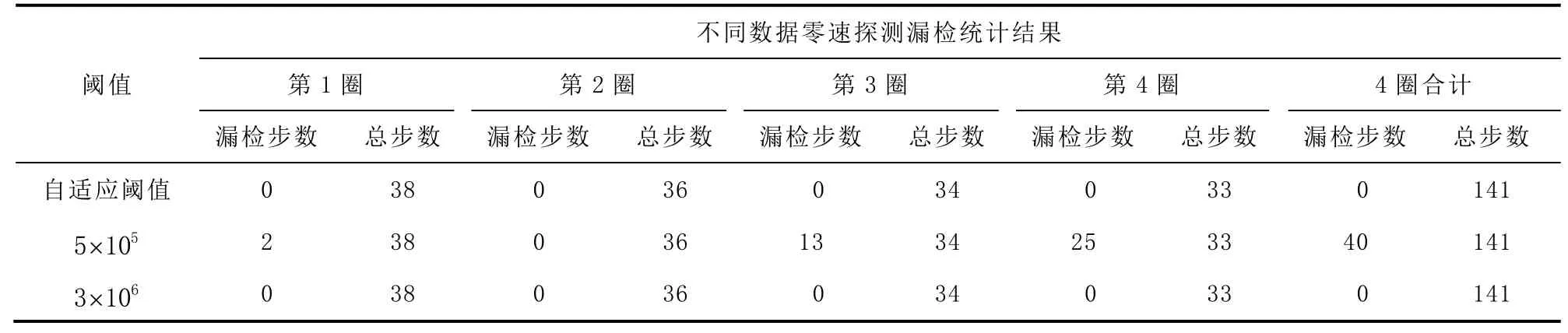
表3 不同零速探测阈值漏检统计表

从图5至图8可以看出，随着平均步行速度加快，检验统计量极小值的均值也变大。在正常行走时，行人每一步的速度可能会受周围环境或其他因素的影响而有明显的变化，仅能保证相对匀速行走。因此在慢速行走时，可能出现某一步速度很快，快速行走时，可能出现某一步速度很慢的现象。自适应阈值aλ能够很好地反映检验统计量的变化特征，对步行速度非常敏感。在上述4组数据中，随着行人平均速度增大，自适应阈值的均值也变大；同一组数据中速度发生变化时，自适应阈值也能进行相应调整，以保证探测效果；数据中存在小步幅时，检验统计值的极小值和幅值都很小的情况，即便用小的固定阈值也会将整步误判为零速状态，而自适应阈值能够及时地调整其大小，避免错误检测。较小的固定阈值1λ，在慢速的情况下，能够判断出几乎所有的零速间隔，但是当行人速度较快时，则存在较多漏检的情况；较大的固定阈值2λ，虽然能保证探测出所有的零速间隔，但是将导致虚警概率PFA过大，容易将运动时刻判断为零速时刻，特别是在行人开始和结束步行时，容易将速度很慢的小步全部探测为零速。

从统计结果来看：自适应阈值不存在将整段零速间隔漏检或将一步全部误判为零速的情况；较小的固定阈值1λ出现过1次将整步误判为零速的情况，但在速度较快的2圈，则存在大量零速间隔漏检的情况；较大的固定阈值2λ，虽然不存在将整段零速间隔漏检的情况，但是存在将第2—4圈的最后一步全部误判为零速状态的情况，也存在将第1圈第1步的部分运动状态误判为零速状态的情况。

3.2 零速修正结果

通过卡尔曼滤波方法对每1圈和4圈数据惯导机械编排结果进行零速修正，测试路线起点为（0 m，0 m），形状为1个直径18 m的圆圈。用解算结果到圆心的距离与参考轨迹半径的差作为水平误差，在解算精度较高时，该方法计算得到的水平误差能够反映真实误差，而在解算结果发散严重时，该方法计算的水平误差较真实误差小。不同阈值的零速修正结果及水平误差如图9至图13所示。

从解算轨迹和水平误差序列来看：在4组测试数据中，用自适应阈值零速探测方法由于不存在漏检或误检的情况，解算轨迹无明显突刺，与参考轨迹接近；在慢速行走、用小的固定阈值1λ时，解算轨迹与参考轨迹比较接近，解算精度与用自适应阈值零速探测结果进行零速修正的解算精度相近；由于第1圈连续漏检了2个零速间隔，导致解算结果存在一处明显的突刺，水平误差超过0.7 m；在快速行走时，由于漏检大量零速间隔，解算结果很快发散导致误差很大，最大误差超过30 m。用大的固定阈值2λ解算4圈轨迹，其结果与参考轨迹行状相近，但由于此时将部分动态判断为静态，错误的速度更新导致轨迹半径较参考轨迹小，其中慢速行走时，解算轨迹直径比参考轨迹小1.5 m左右。单圈和4圈联合解算水平误差的最大值、均值、均方根标准差统计如表4至表7所示。

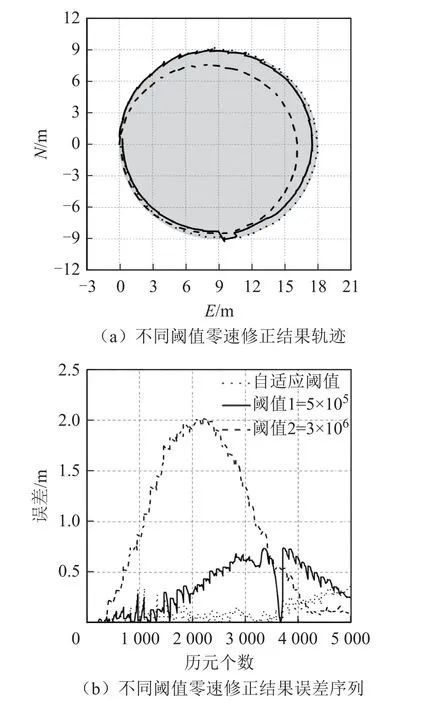
图9 第1圈零速修正效果对比

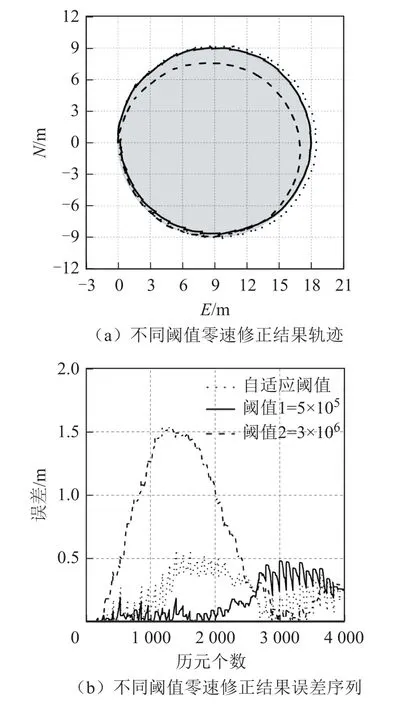
图10 第2圈零速修正效果对比

图11 第3圈零速修正效果对比

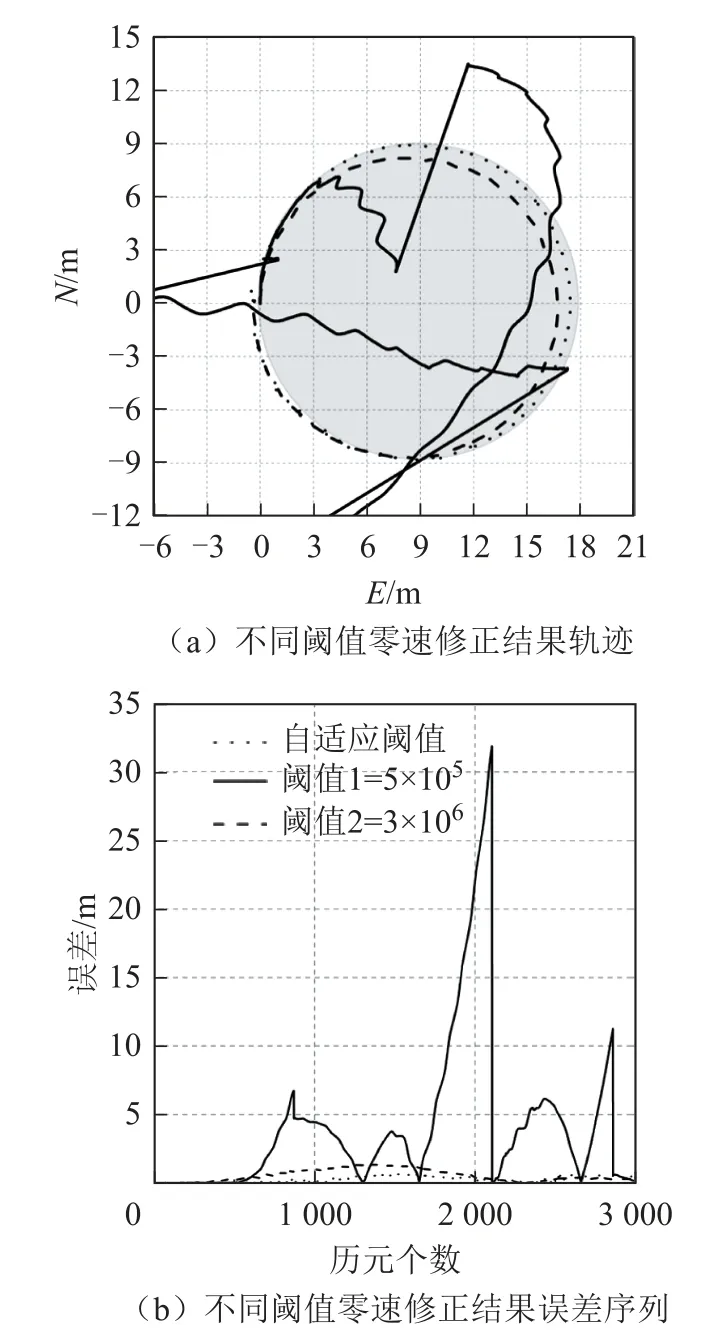
图12 第4圈零速修正效果对比

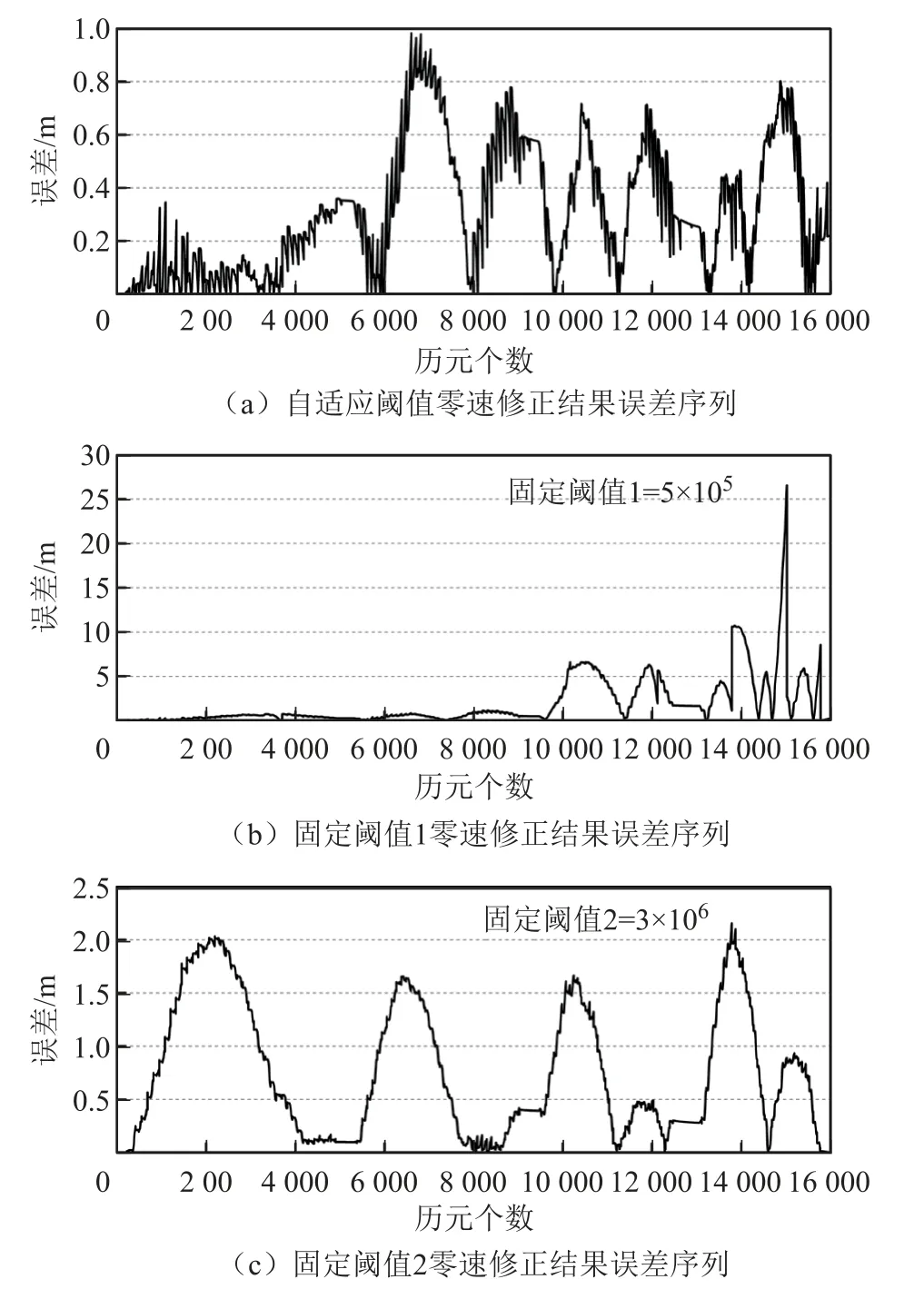
图13 4圈数据不同阈值零速修正结果误差序列

从误差统计结果来看：在慢速行进的2圈中，自适应阈值效果与小的固定阈值的效果相当，明显优于大的固定阈值；在快速行进的2圈中，自适应阈值效果与大的固定阈值的效果相当，明显优于小的固定阈值。从4圈联合解算的零速修正结果来看，自适应阈值保证了不同步行速度下的零速修正效果，平均误差为0.31 m，最大误差不超过1 m，明显优于固定阈值。本文提出的自适应阈值法，通过动态调整阈值，保证了行人不同步行速度状态下的零速修正效果，即便速度短时发生较大变化，也能及时调整到合适的阈值，获得较好的零速修正效果，相对使用固定阈值，本文的方法具有更好的普适性和鲁棒性。

表4 零速修正结果最大误差

表5 零速修正结果平均误差

表6 零速修正结果均方根误差

表7 零速修正结果标准差

4 结束语

本文分析了不同步行速度下，传感器原始数据和检验统计量的特征，确定了利用窗口内检验统计量的最小值和幅值，来计算零速探测阈值的方案，实现了阈值随行人步行速度变化而自动调整，本文方案的计算方法简单、实用。对比分析了自适应阈值、固定阈值的零速探测结果和零速修正效果：小的固定阈值仅在慢速情况下，能获得较理想的零速探测和零速修正结果，在快速步行情况下，则存在大量漏检的情况；大阈值在低速时容易出现错误检测，包括将静止状态前后多个历元误判为零速、将“小步”判断为零速等情况，导致错误的速度约束信息。与固定阈值相比，自适应阈值能随行人步行速度变化而动态调整，零速间隔探测准确度达100%，在不同速度下均能获得较好的零速修正结果，绕直径18 m的圆，以不同速度步行4圈获取了实验数，其解算结果的水平误差不超过1 m，优于固定阈值方法的26.58和2.16 m。