石英挠性加速度计表头力矩器噪声模型研究*

刚 煜， 王永建， 赵 鹏， 贺慧勇， 唐立军

(1.长沙理工大学 物理与电子科学学院，湖南 长沙 410114；2.近地空间电磁环境监测与建模湖南省普通高校重点实验室，湖南 长沙 410114)

0 引 言

石英挠性加速度计是一种用于测量微小加速度的力平衡摆式加速度计，具有测量范围广、精度高，抗干扰能力强等优点，广泛应用于航空、航天、航海及各种武器的导航和控制系统中。随着惯性导航技术的发展，系统对传感器精度的要求越来越高，加速度计作为惯性导航系统中的重要组成部分，其测量精度直接影响到整个系统的精度[1～3]。

石英挠性加速度计的输出信号比较微弱，因此，噪声控制成为高精度石英挠性加速度计系统设计的关键所在，建立精确的噪声模型可以对整个系统特性和性能提供有效的预测，并且对外围电路的测试和优化有很大的帮助。石英挠性加速度计的系统噪声主要包括表头内部噪声和伺服电路噪声。天津航海仪器研究所对高精度加速度计的输出噪声特性进行了分析，阐明了加速度计噪声产生的原因，说明了环境对高分辨率加速度计测试的重要性[4]。长沙理工大学建立了简单的加速度计行为模型[5]，完成了加速度计模型闭环工作仿真，但未分析噪声的影响。

本文针对石英挠性加速度计表头力矩器的噪声进行了研究，探索机械热噪声及其力矩器线圈谐振的影响，建立了石英挠性加速度计表头力矩器噪声模型，为加速度计整体模型的研究提供了参考依据。

1 加速度计表头工作原理

石英挠性加速度计表头主要由挠性杆、石英摆片、力矩器线圈、固定极片组成，当有加速度输入时，挠性杆和石英摆片及力矩器线圈组成的检测组件受到惯性力的作用，位置发生偏转，脱离平衡位置，石英摆片上的动电极与固定极片构成的差动电容值也随检测质量位置的变化而变化，外部处理电路通过检测差动电容信号，并根据差动电容值的变化值将驱动电流加到力矩器线圈上，通过电磁力的作用将石英摆片恢复至平衡位置，其驱动电流的极性由加速度的方向决定[6]。

石英挠性加速度计闭环工作框图如图1示，图中，石英摆片传递函数中的J为摆片组件的转动惯量，C为阻尼系数，K为石英挠性梁的弹性刚度，M1和M2分别为外部加速度与电磁力产生的力矩，a为外部加速度。

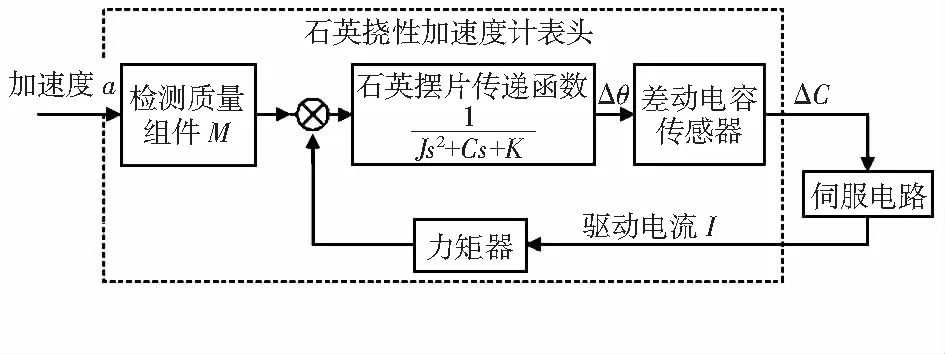
图1 石英挠性加速度计闭环工作框图

根据加速度计表头的工作方式，所建立的行为模型分3个部分，从输入到输出的前后级分别为：激励和外部参数输入部分、系统响应特性部分和输出执行部分。其中，激励和外部参数输入部分用于输入加速度和力矩器驱动电流，系统响应特性部分用于模拟表头的响应特性，最终通过输出执行部分将代表着当前加速度信息的差动电容值输出。因此，加速度计表头的行为模型必须考虑内部力矩器噪声影响。

2 加速度计表头力矩器噪声分析

2.1 机械热噪声

机械热噪声主要与受影响器件的结构设计、外界环境等因素有关[7,8]。对于石英挠性加速度计表头，其检测质量组件周围分布着气体分子，气体分子的布朗运动会引起机械热噪声，从而产生机械热噪声等效加速度和力矩作用于检测质量组件。根据热力学理论，石英挠性加速度计检测质量组件机械热噪声谱密度Stn(N2/Hz)为

(1)

则热噪声的等效加速度atn(m/s2)为

(2)

式中KB为玻尔兹曼常数1.38×10-23J/K；T为热力学绝对温度，K；m为检测质量组件的质量；C为机械阻尼系数，N·s/m；B为工作带宽。根据式(2)可知，机械热噪声等效加速度的大小主要由热力学温度及机械阻尼系数决定，在表头设计过程中，减少检测质量组件的质量、降低器件工作温度、减小阻尼可以减少表头内部的机械热噪声。

假定表头检测组件(包括石英摆片和力矩器线圈)的整体质量为800 mg，温度取300 K，阻尼系数取0.008 N·S/m时，则机械热噪声等效加速度a最大幅值为5×10-9m/s2。

2.2 力矩器线圈谐振

为使检测质量组件平衡至中间位置，力矩器上有线圈，当输入驱动电流时会产生电磁力与组件受到的惯性力平衡，而力矩器线圈可视为具有一定大小的电感、寄生电容器、电阻器串联的RLC回路，RLC串联电路具有选频特性，当力矩器的驱动电流频率满足RLC电路固有频率时，会发生谐振，对后续输出造成影响[9，10]。

对RLC串联电路，有如下参数反映电路的频率特性：谐振频率f0、通频带宽BW以及品质因数Q，且满足

(3)

BW=fH-fL

(4)

(5)

式中R为力矩器线圈电阻值；C为力矩器线圈寄生电容值；fH和fL分别为电路中电流由最大值减小3 dB时所对应的上限截止频率和下限截止频率；ω0为谐振频率。结合式(3)和式(5)分析可知，力矩器线圈谐振频率的大小取决于线圈寄生电容值和电感量的大小，而品质因数Q影响力矩器线圈的选频性，Q值越大，线圈的通频带越窄。

3 力矩器模型的建立

3.1 机械热噪声模型

影响机械热噪声的因素主要为温度、阻尼系数及质量，在机械热噪声模型中，温度、阻尼系数使用电信号模拟。模型的输入为温度、阻尼系数、惯性加速度，输出为叠加热噪声之后的加速度信号。如图2所示，Inoise为根据温度T和阻尼系数f产生的等效热噪声加速度信号，与输入的惯性加速度Iacc叠加后输出。

图2 机械热噪声电路模型

3.2 力矩器线圈模型

线圈的分布电容值由匝间电容值和层间电容值组成，其中，匝间电容值是线圈同一层各匝之间的分布电容值，而层间电容值是线圈不同层之间的分布电容值。对于线圈匝间电容器均为串联状态，而层间电容器之间为并联状态，根据电路原理可知，当电路中有多个电容器串联时，其等效电容值较小，在计算总的分布电容值时可以忽略串联的匝间电容值，对于线圈分布电容值来说，层间电容值占主要部分[11]。

设力矩器线圈的排绕方式为“Z”型,其等效分布电容值为

(6)

式中N为每层线圈的匝数；D为线圈导线截面的直径；d为层与层之间的间距；l为每匝线圈的长度；n为线圈层数；εr和ε0分别为线圈线漆和真空的介电常数。表1列出根据某款石英挠性加速度计力矩器线圈规格计算出的线圈各物理量数值[12]。

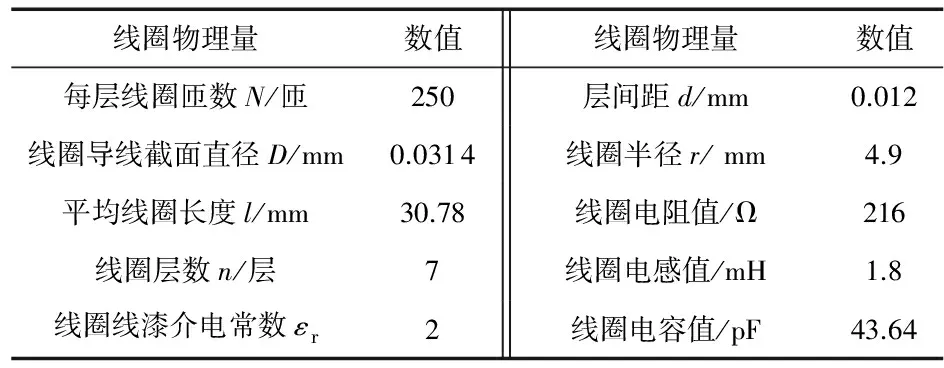
表1 力矩器线圈参数

根据计算的R，L，C参数建立力矩器线圈的电路模型如图3所示，Iin为外部伺服电路反馈电流的输入端，out为力矩器线圈的输出端。

图3 力矩器线圈电路模型

4 力矩器模型测试

4.1 模型仿真测试电路

结合上述机械热噪声和线圈的电路模型，将其整合为力矩器噪声模型，搭建了图4的测试电路对力矩器模型进行测试。模型的输出Iout为叠加热噪声之后的加速度信号，Ain为加速度输入端，Iin和In为加速度计力矩器线圈驱动电流的输入端，为模拟脉宽调制(pulse width modulation,PWM)驱动方式对模型的影响，使用Iin产生峰峰值为3.3 V、偏置为1.65 V的方波信号。

图4 力矩器噪声模型测试电路

4.2 机械热噪声模型测试分析

分别设置温度为300 K，阻尼系数为0.008 N·S/m和温度为100 K，阻尼系数为0.008 N·S/m进行测试，结果如图5，阻尼系数一定时，机械热噪声随温度增加而增加，对力矩器模型输出信号的扰动变大，符合式(2)的计算结果。

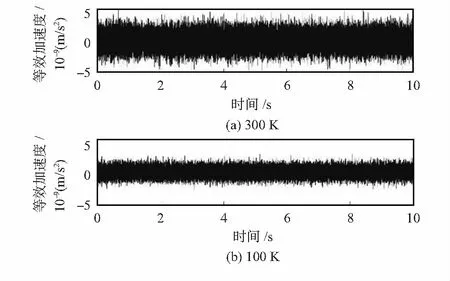
图5 机械热噪声模型测试结果

4.3 力矩器模型测试分析

在力矩器模型测试中，分别采用了PWM波和正弦波2种驱动方式作为输入信号(Iin)，对应输入电压为Uin，其输出信号(roil)反映了力矩器线圈中电流的谐振情况，Iout反映了叠加了热噪声后力矩器模型的总输出。验证结果如图6，图6(a)、图6(b)、图6(d)为力矩器驱动信号在50 Hz,10 kHz和600 kHz时，驱动方式为PWM波的力矩器电流信号输出；图6(c)为力矩器驱动信号在10 kHz时，驱动方式为正弦波的力矩器电流信号输出。

图6 力矩器模型测试结果

从图6可知，当力矩器采用PWM的驱动方式时，力矩器线圈的谐振电流较采用正弦波驱动要大，且在驱动频率在谐振点之外时，最大会产生近600 μA的电流；当驱动频率靠近谐振点562.34 kHz时，其内部产生的谐振电流最大，达到4 mA。此外，300 K时力矩器的机械热噪声等效加速度，最大幅值将近0.05 ngn(5×10-10m/s2)，说明对石英加速度计表头来说，驱动方式的谐振影响较机械热噪声的影响更大，在设计加速度计数字化电路时，需考虑该因素。

5 结束语

石英挠性加速度计力矩器的噪声对于高精度加速度计电路有重要影响。本文从理论上分析了石英挠性加速度计内部检测组件的力矩器的噪声影响，从机械热噪声和线圈谐振两方面分析建立了电路模型，设计了测试电路对模型进行了测试，从理论和实验上验证了表头力矩器噪声电路模型的正确性。该噪声电路模型可以进一步完善石英挠性加速度计整体行为模型，具有一定的应用价值。

[1] 高雅彪,毛伟玲,李醒飞.石英挠性摆式加速度计闭环检测电路设计[J].电子技术应用,2012(2):70-72,76.

[2] 朱海燕,叶凌云,彭皓岚,等.石英挠性加速度计数字闭环控制研究[J].传感器与微系统,2015，34(8):61-63，79.

[3] 张 晞,张声艳,曹巧媛.数字闭环石英挠性加速度计量化误差分析与实验研究[J].传感器与微系统,2013,32(11):33-36.

[4] 侯文超,刘晓东,吴 畏,等.石英挠性加速度计输出噪声特性分析[J].舰船电子工程,2015(3):39-42，69.

[5] 商梅雪,贺慧勇,唐立军,等.石英挠性加速度计表头行为模型研究[J].电气工程,2016,4(1):81-89.

[6] Chen Fubin,Zhang Kebei.Identification for temperature model and the method for temperature compensation of quartz flexible accelerometer[C]∥Proceedings of 2015 IEEE Advanced Information Technology,Electronic and Automation Control Conference,IAEAC 2015,IEEE Beijing Section,Global Union Academy of Science and Technology,Chongqing Global Union Academy of Science and Technology,2015:5.

[7] 张 霞,闫社平.微机械加速度计内部噪声影响的对比分析[J].西安邮电学院学报,2012(2):57-61.

[8] 杨丹琼,陈志龙,徐 静,等.低热机械噪声MEMS加速度计设计[J].传感器与微系统,2011,30(11):89-91，95.

[9] 祁国权.RLC串联电路谐振特性的Multisim仿真[J].电子设计工程,2012(1):39-41.

[10] 侯卫周,谷 城,金玉川.基于电子电路谐振现象的品质因数意义的探究[J].电子科技,2010(2):59-60，64.

[11] 陈 龙,赵艳美,张 宁.一种计算电感线圈分布电容的简化模型[J].南京师范大学学报：自然科学版,2014(2):55-59.

[12] 李 安.石英挠性加速度计关键技术研究[D].杭州：杭州电子科技大学,2011.