基于标架场理论的完整系统Boltzmann-Hamel方程简化方法研究∗

张素侠 陈纬庭

1)(天津大学机械工程学院力学系,天津市非线性动力学与混沌控制重点实验室,天津 300354)

2)(天津大学建筑工程学院土木工程系,天津 300354)

1 引 言

Boltzmann-Hamel方程(以下简称为B-H方程)是由Boltzmann于1902年提出的一种完整系统运动方程[1],后经Hamel推广到非完整系统[2,3].20世纪80年代到90年代,B-H方程的研究主要集中于几何化[4]、变质量系统[5−7]、非惯性系[8]、单面非完整约束系统[9]和高阶非完整系统[10,11].21世纪初,完整和非完整系统B-H方程的对称性解法取得了很大进展,通过将Lie对称性、Noether对称性和形式不变性引入B-H方程中以构造相应的守恒量,简化了B-H方程的求解,其中典型的工作如文献[12—15].与此同时,在应用方面 B-H方程又出现在弹性力学[16]、非完整控制[17]和辛算法[18]的研究中.这些研究关注的焦点均是准速度与非完整约束相似的结构,却鲜有文献关注准坐标的选取对B-H方程形式的影响.

文献[19]首次提出了准坐标在选取上的自由性.本文研究证明:准坐标自由性的推广,可以使完整系统的B-H方程得到尽可能的简化.利用标架场理论,从几何不变性的角度直接导出了完整系统中的B-H方程,并从流形均匀性的角度出发,证明了对于任意广义力为零的均匀构形空间,以及任意广义力不为零的零曲率构形空间,一定可以找到某个准速度或准坐标,使其中的B-H方程化简为可积分的形式.同时给出具体的简化方法并举例说明本方法的适用性.

2 构形空间中的标架场与B-H方程

设本文研究的构形空间是M,其中的广义坐标是q1,···,qn.将M建模为n维Riemann流形[20],则Riemann度量可利用广义坐标qi表示为

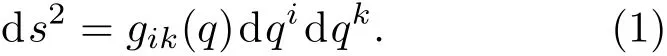
即广义坐标基矢场{∂/∂qk}下的Lagrange方程是

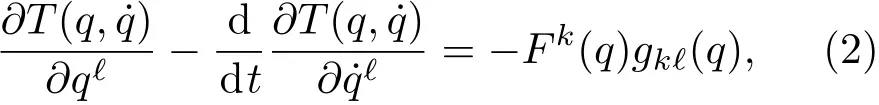
其中T是动能,而Fk(q)是外力.将方程(2)展开为如下分量表述的形式:

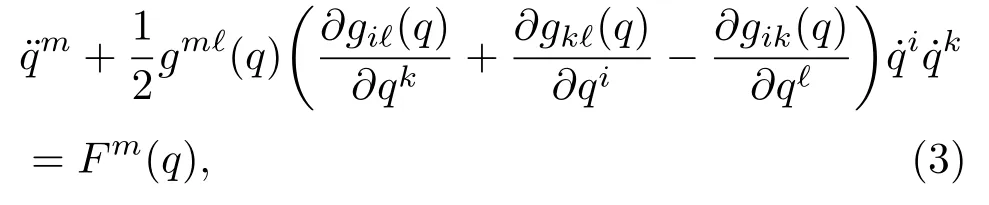
利用Christoffel符号可将Lagrange方程简写为

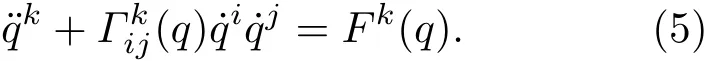
下面引入构形空间中的标架场,即构形空间中n个处处线性无关的矢量场.从标架场的定义可以发现,其与坐标基底的区别在于它可能不是由某组广义坐标生成的.因为标架场本质上也是矢量场,则可以将标架场在广义坐标基底场下展开为

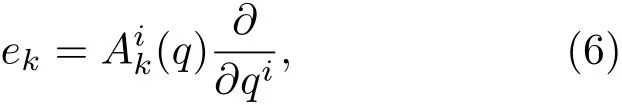
对于完整标架场,可以表示为某组广义坐标的坐标基底场.现在通过标架系数定义Frobenius符号

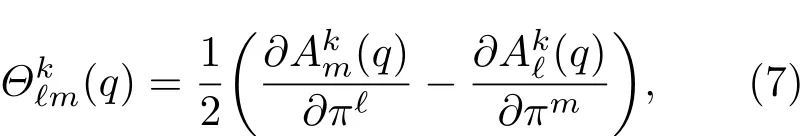
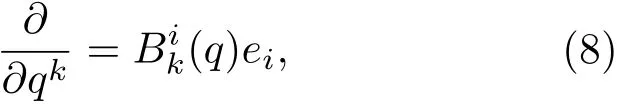
可积分,反之则不是完整的.从几何的观点来看,标架场是坐标基底场的线性推广.

现在使用标架场作为基底来展开构形空间中的速度矢量

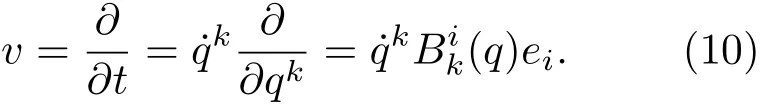
将构形速度矢量在标架场下的分量记为˙πi,即有

这就是准速度.即准速度的几何本质就是速度矢量在标架场下的分量.如果说广义速度对应着广义坐标基底场,那么准速度就对应着标架场.在(11)式两边同时乘上dt,得到

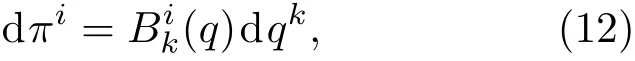
当标架场{ek}是完整标架场时,(12)式中的dπi是全微分,解出πi=πi(q)就等于进行了一个广义坐标变换q→π,此时准坐标π称为完整准坐标,本质上就是广义坐标;而当标架场{ek}是非完整标架场时,准坐标π没有具体的意义,只是形式上写成π,即对于非完整标架场,并不严格区分准速度与准坐标,两者本质上是相同的.

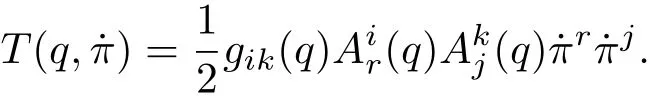
因为Lagrange方程是构形空间中的张量方程,它对于构形空间中的广义坐标变换保持不变,现在视准坐标为新的坐标,标架系数为广义坐标变换的Jacobi矩阵分量,即可得到利用准速度表述的B-H方程

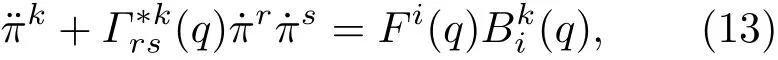
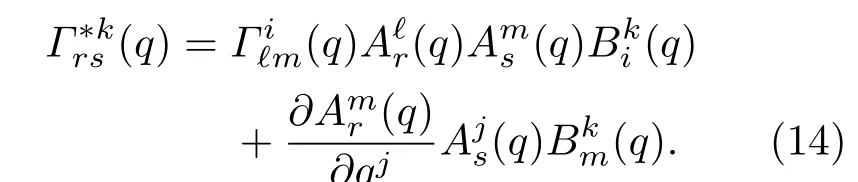
(14)式是将Christoffel符号在广义坐标变换下的变换式(Q是新广义坐标)

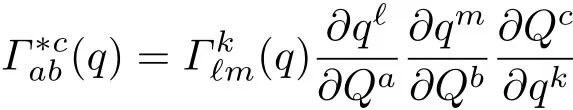
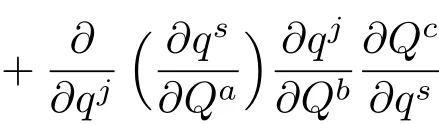
中的∂qm/∂Qb替换为而得到的.

3 化简B-H方程的方法

求解完整系统的B-H方程的通用做法是将(11)式代入到(13)式中构造关于广义坐标q的微分方程组.但是对比方程(5)和(13),发现方程(13)中加入了标架系数和逆标架系数而这些系数的选取是完全任意的,那么通过系数的选取可以使B-H方程得到简化:在方程(13)中就能解出准速度接下来只用去处理简单的线性方程这就要求B-H方程应为如下形式:

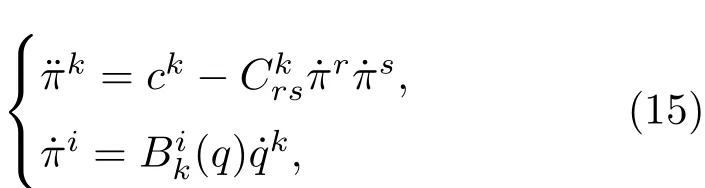
定理1 对于任意广义力为零的均匀构形空间,总可以找到某个准坐标π,使得方程(15)成立(ck=0).

证明 设初始的广义坐标就是均匀空间中的容许坐标.在任意均匀空间中一定存在某个标架场{ek},满足下式[22]:

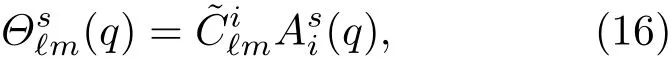
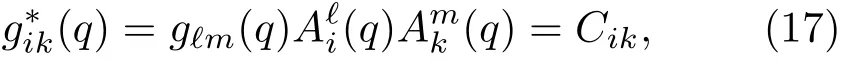
其中常张量Cik是由结构常数决定的.将(17)式代入到(14)式中可以得到

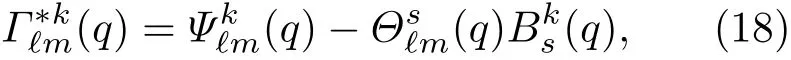
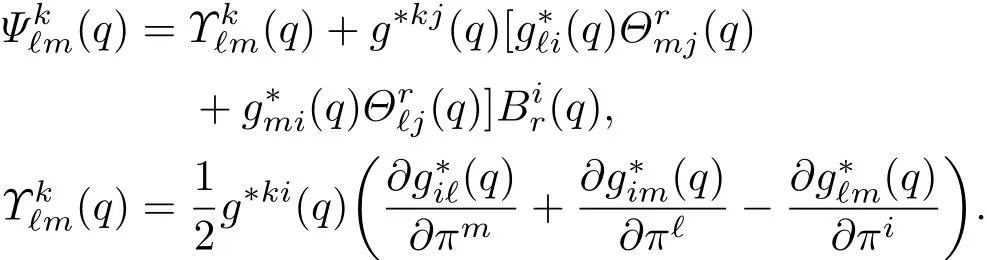
即在标架场{ek}下全是常数,也即方程(15)成立.而定理1中所求的准速度就是速度矢量在标架场{ek}下的分量.证毕.

通过定理1,只要判定了所研究的构形空间是均匀空间,就可以根据该均匀空间的结构常数来导出简化B-H方程的准坐标和常数在实用中最常见的是常曲率构形空间(均匀空间的特例),这时可通过计算构形空间的内禀曲率来判定其是否为均匀空间.其中一种特别重要的情况是方程(15)中常数全为零,这时可以考虑广义力存在的情况.给出定理2.

定理2 对于任意零曲率的构形空间,都可以在其中找到一个完整的准坐标π,使方程(15)在该坐标下表示为

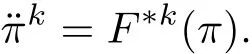
证明 标架场{ek}下的曲率张量有分量

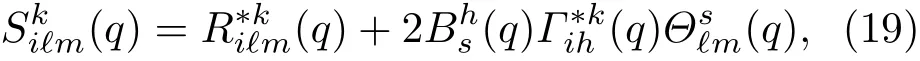
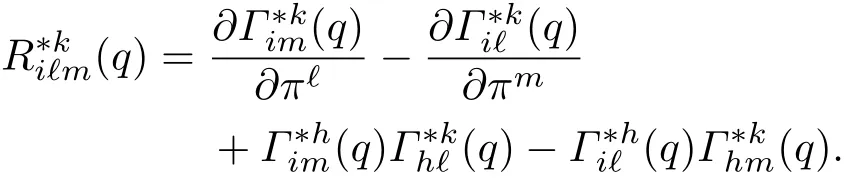
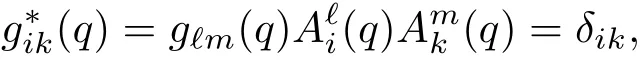
其中δik是单位张量分量.这样有0,即将归零了.此时在中仅剩下一项

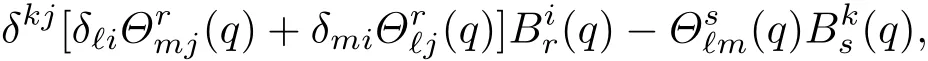
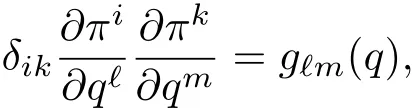
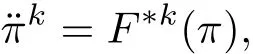
这即为定理2中要求的形式,证毕.

4 算 例

例1 考虑某两个自由度的力学系统,该系统的广义坐标取q1和q2.给出这个力学系统的Lagrange函数

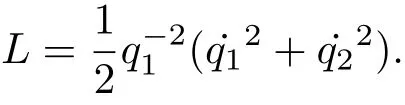
该系统没有广义力,对应的构形空间的度量张量在广义坐标q下表示为

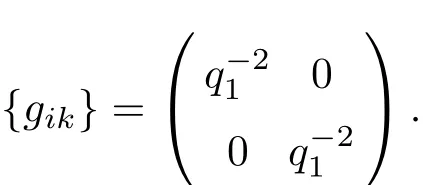
代入Lagrange方程(2),得到下述方程组:

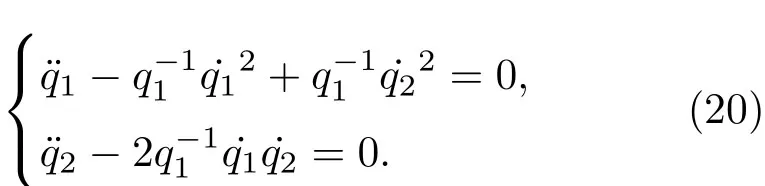
将gik代入到(4)式中计算Christoffel符号,再利用这些Christoffel符号计算此时的曲率张量,发现该构形空间是负常曲率空间(曲率为−1),所以根据定理1,方程(20)可积分.引入以下准速度:

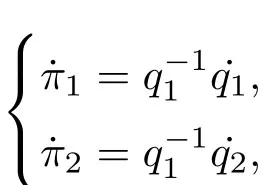
进行变量替换就得到了用准速度˙π坐标表示的B-H方程:

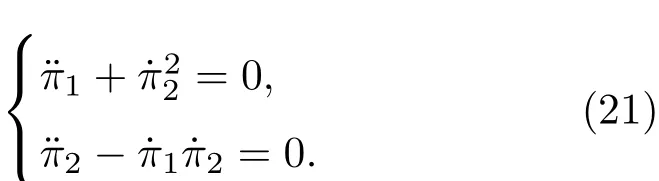
准速度解为(其中a,b是积分常数):

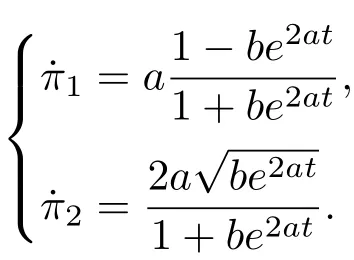
接下来只需求解下述一阶线性方程:

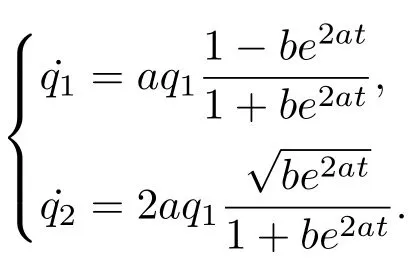
很明显该线性方程存在积分解.

例2 考虑某三个自由度的力学系统,该系统的广义坐标取q1,q2和q3;惯量用m表示,相互作用常数用k表示.给出这个力学系统的Lagrange函数

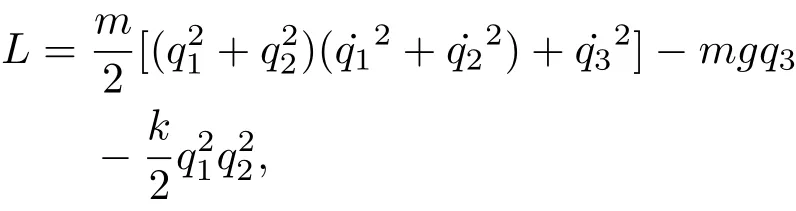
即该力学系统对应的构形空间的度量张量在广义坐标q下表示为

2.强化政策保障。积极争取国家电子商务发展扶持政策倾斜我市，最大限度支持全市商贸流通业线上线下互动创新发展。在保证政策连续性的基础上适时研究调整市内商贸流通业线上线下互动创新发展扶持政策，从财政、投融资、用地等方面给予更大支持。

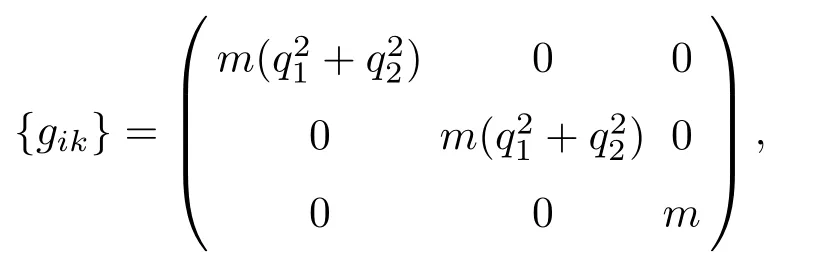
代入Lagrange方程(2),得到下述方程组:

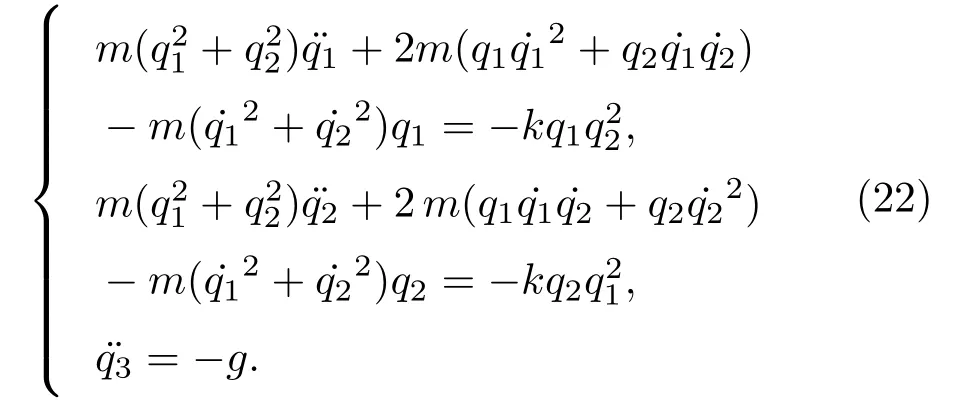
计算得到此时的曲率张量分量全是0.根据定理2,引入以下完整准坐标:

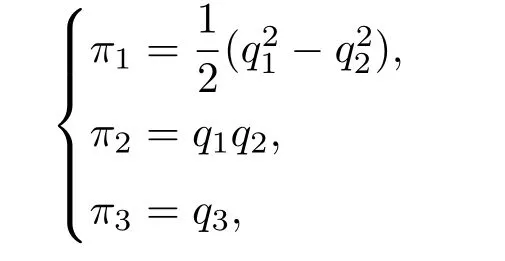
进行变量替换就得到了用完整准坐标π坐标表示的B-H方程:

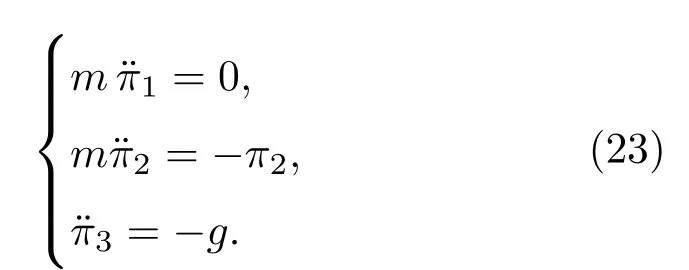
该B-H方程有以下解析解(其中的a,b,c,d,e,f均是积分常数):

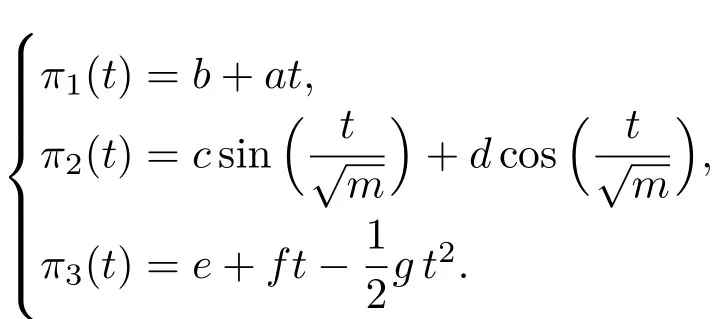
对比方程(20)和(21),(22)和(23)可以发现,采用本文提出的方法进行变换,可以大大简化运动方程的形式,以求得解析解.

5 讨 论

通过前面的理论推导和算例分析,可以看到本文方法具有数学和物理两方面的意义.

从数学的角度来看,原有的分离变量方法和对称性方法均是给出合适的广义坐标来分离变量或构造守恒量以简化运动方程.而本文提出的方法则是将广义坐标推广为准坐标,进而将Lagrange方程推广为B-H方程,给出合适的准坐标来简化B-H方程,此时得到的结果更具有普遍性.

值得说明的是,定理1和定理2中给出的最简标架场的构造方法,需要利用均匀构形空间自身的结构常数,即在标架场平移下度量张量分量的不变性;而经典的广义动量积分讨论的则是力学系统的Lagrange函数在广义坐标平移下的不变性所导出守恒量,在广义力为零时,前者给出的标架场可作为后者寻找守恒量的有力工具.而经典的广义能量积分是时间平移不变性所导出的守恒量,与本文的结果无关.

6 结 论

本文从几何不变性的角度直接导出了完整系统中的B-H方程,并说明了可以在任意广义力为零时的常曲率构形空间和广义力不为零时的任意零曲率构形空间中找到某个标架场,使该标架场生成的准速度简化B-H方程到可积分的形式.即对于复杂的运动方程,要先尝试计算构形空间的内禀曲率.若满足定理1和定理2中提出的条件,可找到该运动方程的解析解.本文的方法为寻找运动方程解析解提供了一条新途径.

[1]Boltzmann L 1902Sitz.Math.Natur.Akad.Wiss.B11 1603

[2]Hamel G 1904Math.Phys.50 1

[3]Hamel G 1938Art.Sitz.Math.Ges.37 4

[4]Tang C L,Shi R C 1989J.Beijing.Inst.Tech.9 35(in Chinese)[唐传龙,史荣昌1989 北京理工大学学报9 35]

[5]Qiu R 1997Appl.Math.Mech.18 1033(in Chinese)[邱荣1997应用数学和力学18 1033]

[6]Lü Z Q 1994Jiangxi Sci.12 195(in Chinese)[吕哲勤1994江西科学12 195]

[7]Zhou R L,Chen L Q 1993J.Anshan.Ins.I.S.Tech.16 46(in Chinese)[周瑞礼,陈立群 1993 鞍山钢铁学院学报16 46]

[8]Zhang J F,Zhang H Z 1990J.Zhejiang Norm.Univ.(Nat.Sci.Ed.)13 61(in Chinese)[张解放,张洪忠1990浙江师范大学学报(自然科学版)13 61]

[9]Zhang Y,Wu R H,Mei F X 1999Shanghai J.Mech.20 196(in Chinese)[张毅,吴润衡,梅凤翔 1999 上海力学20 196]

[10]Mei F X 1985The Foundations of Mechanics of Nonholonomic System(Beijing:Beijing Institute of Technology Press)pp87–89(in Chinese)[梅凤翔 1985 非完整系统力学基础 (北京:北京工业学院出版社)第87—89页]

[11]Zhang J F 1990Huanghuai.J.6 13(in Chinese)[张解放1990黄淮学刊6 13]

[12]Fu J L,Liu R W,Mei F X 1998J.Beijing Inst.Tech.7 215

[13]Fu J L,Liu R W 2000Acta Math.Sci.20 63(in Chinese)[傅景礼,刘荣万2000数学物理学报20 63]

[14]Fu J L,Chen L Q 2004The Progress of Research for Mathematics Mechanics Physics and High New Technology(Vol.2004(10))(Chengdu:Southwest Jiaotong University Press)pp124–132(in Chinese)[傅景礼,陈立群2004 数学·力学·物理学·高新技术研究进展2004(10)卷(成都:西南交通大学出版社)第124—132页]

[15]Xu X J,Mei F X 2005Acta Phys.Sin.54 5521(in Chinese)[许学军,梅凤翔 2005物理学报 54 5521]

[16]Xue Y,Liu Y Z,Chen L Q 2006Acta Phys.Sin.55 3845(in Chinese)[薛纭,刘延柱,陈立群 2006物理学报55 3845]

[17]Zhang Q,Liu Z B,Cai Y 2008Chin.J.Aeronaut.21 471(in Chinese)[战强,刘增波,蔡尧 2008 中国航空学报21 471]

[18]Xie J F,Pang S,Zou J T,Li G F 2012Acta Phys.Sin.61 230201(in Chinese)[谢加芳,庞硕,邹杰涛,李国富2012物理学报61 230201]

[19]Jarzebowska E M 2015Selected Papers from CSNDDAgadir,Morocco,May 21–23,2014 p167

[20]Arnold V I(translated by Qi M Y)2006Mathematical Methods of Classical Mechanics(4th Ed.)(Beijing:Higher Education Press)pp59–69(in Chinese)[阿诺尔德 著(齐民友 译)2006 经典力学的数学方法(第四版)(北京:高等教育出版社)第59—69页]

[21]Chern S S,Chen W H 2001Lectures on Differential Geometry(2nd Ed.)(Beijing:Peking University Press)pp30–38(in Chinese)[陈省身,陈维桓 2001 微分几何讲义(第二版)(北京:北京大学出版社)第30—38页]

[22]Landau L D,Lifshitz E M(translated by Lu X,Ren L,Yuan B N)2012The Classical Theory of Fields(8th Ed.)(Beijing:Higher Education Press)p426(in Chinese)[朗道,栗弗席兹 (鲁欣,任朗,袁炳南 译)2012场论(第八版)(北京:高等教育出版社)第426页]