引力彩虹时空中Kerr黑洞的熵谱和面积谱∗

刘成周 邓岳君 骆叶成

(绍兴文理学院物理系,绍兴 312000)

1 引 言

黑洞的熵谱和面积谱是黑洞量子性质的重要内容.通过考虑黑洞吸收或释放试验粒子,贝肯斯坦(Bekenstein)首先提出了最小面积增量为ΔA=εħ的黑洞事件视界的等间距面积谱[1,2].其中,ε是一个无量纲常数,ħ为普朗克常量,且采用了c=G=1的自然单位制.进一步,贝肯斯坦指出,对于一个均匀缓慢演化的黑洞,视界面积是一个绝热不变量[3,4].也就是说,相比于外部的扰动变量,黑洞自身的面积变化是非常缓慢的.根据Ehrenfest原理,任何经典的绝热不变量都对应一个有离散谱的量子属性.这样可以得出黑洞面积是量子化的,面积量子是εħ.并且,用这种方法得出的面积增量是

将贝肯斯坦面积谱(1)与黑洞的贝肯斯坦-霍金(Bekenstein-Hawking,B-H)公式

相结合,则可得到等间距的黑洞熵谱

将黑洞视界面积的绝热不变性和黑洞的准正则模相结合,Kunstatter[5]提出了一个黑洞绝热不变变量公式.该公式表明,对于一个能量为E和扰动频率为ω(E)的系统而言,自然地有一个绝热不变量

黑洞的准正则模是黑洞受外界扰动时产生的一系列由黑洞本身参数确定的特征频率[6].作为一个半经典极限,可以把一个具有跃迁频率的黑洞考虑为一个周期性的绝热经典系统,且该经典系统的周期由黑洞的准正则模给出.这样,通过玻尔-索末菲量子化通则,可得到作用量I=2πnħ,由此可计算出黑洞熵谱和面积谱.应当指出,利用准正则模研究黑洞量子化的方法是由Hod[7,8]首先提出的.基于玻尔的对应原理,Hod认为,黑洞的高阻尼准正则模对应于系统的量子跃迁,并且渐近的准正则模的实部对应于黑洞的量子跃迁频率.这样,让黑洞的能量变化等于辐射能量,就可以得到黑洞的面积谱.进一步,Maggiro[9]认为,在半经典的极限下,黑洞的跃迁频率应当对应作为复数的准正则模的绝对值.而对处于高激发态的黑洞,准正则模的虚部远大于实部,从而黑洞的特征频率应该来自准正则模的虚部.这是黑洞量子化的准正则模方法的一个重要进展.另外,文献[10]也较早地指出用准正则模的虚部给出黑洞的特征频率.利用准正则模的虚部给出黑洞的特征频率,将其代入(4)式的绝热不变量,并对该绝热不变量进行量子化,可以得到与原始贝肯斯坦谱(1)式一致的黑洞面积谱[9,11,12].利用黑洞准正则模和绝热不变性相结合,对黑洞量子化和黑洞光谱学,在多种时空中进行了广泛研究[13−21].

另外,受贝肯斯坦关于黑洞面积是一个绝热不变量观点的启发,在黑洞量子谱的研究方面,人们还提出了不同的获得黑洞绝热不变量的公式和方法[22−27].其中,通过考虑粒子在事件视界上的隧穿,Majhi和Vegenas[27]给出黑洞的一个绝热不变量

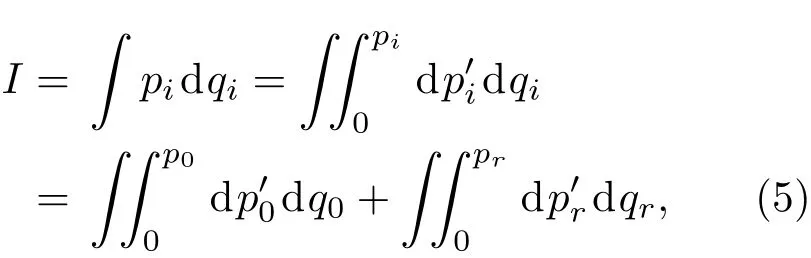
其中pi是坐标qi的共轭动量,q0=τ是欧氏时间,qr=r是径向坐标.对于不带电的静态球对称黑洞,将玻尔-索末菲量子化通则应用于作用不变量(5)式,得到了(3)式所表示的黑洞熵谱[27].这样,通过给出一种绝热不变性,Majhi和Vegenas[27]提出了研究黑洞量子化的一种简便方法.利用这种方法,不使用黑洞的准正则模就可以得到黑洞的量子化谱.考虑作用变量的正则不变性,(5)式的绝热不变量被表述为[28]

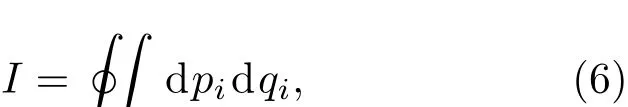
其中qi是欧氏空间中的动力学自由度.这里的积分路径是封闭的,回路靠近且包围事件视界.在静态球对称时空中,利用绝热不变量(6)式,可得到与利用(5)式一致的黑洞熵谱与面积谱[28].利用(5)和(6)式,在不同时空中计算和分析黑洞的绝热不变的作用量,Majhi和Vegenas的方法得到了应用和推广[27−32].在不同的时空中,均得到了(3)式的等间距熵谱,但在考虑黑洞熵的量子修正等引力量子效应时,得到的面积谱是非等间距的,出现了对面积量子(1)式的修正和偏离.

本文将Majhi和Vegenas研究黑洞光谱学的方法应用到引力彩虹时空中的Kerr黑洞.引力彩虹时空具有通过粒子能量依赖性体现的时空量子效应.本文的主要目的是考察时空的能量依赖性对转动时空光谱学的影响.通过给出引力彩虹Kerr黑洞的绝热不变量公式(6)并对其量子化,不考虑黑洞的准正则模,得到了黑洞的熵谱和面积谱.结果表明,引力彩虹Kerr黑洞的熵谱没有粒子能量的依赖性,是与原始贝肯斯坦谱(3)式相同的等间距谱.然而,受时空量子效应的影响,面积谱是依赖于黑洞面积的非等间距谱.结果表明,随着黑洞面积的减少,面积间隔将减少.而当忽略时空的量子效应时,面积谱可以回到等间距的原始贝肯斯坦谱(1)式.通过分析面积谱,给出了普朗克量级的黑洞最小面积.而且得到当黑洞达到最小面积时,面积间隔为零,这表示黑洞辐射的停止和黑洞剩余的出现.与黑洞熵谱一致的是,面积谱也没有粒子能量的依赖性.对引力彩虹Kerr黑洞的熵进行了讨论,得到了包含修正项的黑洞熵表达式.可以看出,黑洞熵的修正与黑洞面积谱的修正均来自时空的量子效应,具有内在一致性.本文第2部分简要介绍引力彩虹时空;第三部分计算引力彩虹Kerr黑洞的作用量和熵谱;第四部分给出Kerr黑洞的面积谱,并讨论黑洞剩余和黑洞熵;最后是总结和讨论.文中采用G=KB=c=1的自然单位制.

2 引力彩虹时空

引力彩虹是时空量子化的一种具体体现.实现引力与量子理论的统一是当前理论物理面临的重大挑战.一般认为,存在一个具有普朗克长度量级的最小长度单元是量子引力的一个基本特征[33],这可从量子引力的基本理论和结果中得到体现.作为量子引力理论的两个主要候选者,弦理论[34,35]和圈量子引力[36]均给出了具有普朗克长度量级的最小可观测长度.另一方面,黑洞物理是量子引力理论的重要试验场.考虑引力的量子效应,用半经典方法研究黑洞物理的量子修正,有可能为量子引力理论的最终形成提供有价值的借鉴和参考.这方面有许多新的尝试和进展[37−46].

最小可观测长度的存在引发了对狭义相对论的修改,并导致了修改狭义相对论的出现[47−51].修改狭义相对论不但要求存在不变的最高速度——光速,而且要求有不变的最高能量——普朗克能量,因此也被称为双狭义相对论.作为修改狭义相对论的主要内容,通常的能量动量不变关系式被修改为

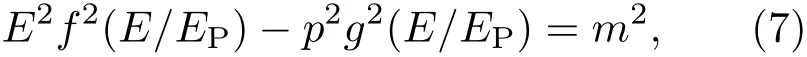
其中,E表示粒子的能量,EP为普朗克能量,p和m分别为粒子的动量和质量.可以看出,在修改狭义相对论中,具有不同能量的粒子将具有不同形式的能量动量关系式,也就说,修改的色散关系是能量依赖的.

修改的色散关系是在动量空间进行定义的,为了给出与该非线性的动量变换定理所在的动量空间对偶的坐标空间,提出了彩虹度规[52,53].彩虹度规可以通过要求动量和无限小位移的缩并满足线性不变关系而得到.相应的平直时空度规可表示为

(8)式表明,时空线元以粒子的能量为参量,用不同能量的粒子作探测粒子,将会对时空有不同的有效描述,该能量依赖的度规族被称为彩虹度规.这就是说,与动量空间对偶的不是单一的时空,而是一个能量依赖的时空族.将彩虹度规推广到包含引力的情况,就可以得到引力彩虹[53].在引力彩虹时空中的Schwarzschild黑洞度规为

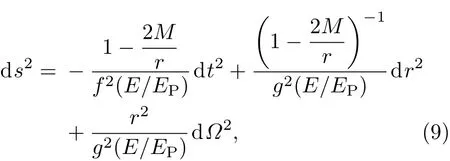
其中,M表示黑洞的质量.与平直的彩虹度规类似,在引力彩虹时空中,通常的经典Schwarzschild黑洞时空被由E/EP作为参数的单参度规族所取代.这样,弯曲时空几何就获得了具有能量依赖性的有效描述.

引力彩虹的能量依赖性体现了引力彩虹的时空量子效应,而且是通过能量函数f(E/EP)和g(E/EP)来具体表示.对于修改的色散关系和引力彩虹中能量函数的具体函数形式,已有多种方案被提出[54].但是,在不同的方案中,f(E/EP)和g(E/EP)都将在低能极限下趋于1.这样,修改的色散关系式就可以在低能极限下回归到通常的能量动量关系式,引力彩虹也回到通常的经典时空.其中,Amelino-Camelia等[55,56]提出

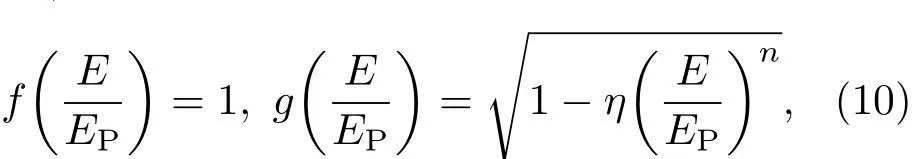
式中η为无量纲常数.对该修改的色散关系及其对应的彩虹时空的含义和理论背景已有深入探讨[56].接下来,利用(10)式表达的修改色散关系,讨论引力彩虹时空中Kerr黑洞光谱学的量子引力效应.

3 引力彩虹时空中Kerr黑洞的熵谱

经典Kerr黑洞由总质量M和总角动量J两个参数来描述.在引力彩虹时空中,Kerr黑洞的轴对称度规在Boyer-Lindquist坐标下可表示为[57]

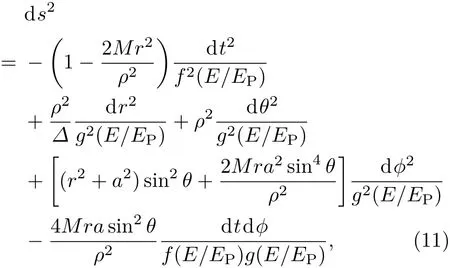
其中,ρ2≡r2+a2cos2θ,Δ≡r2+a2−2Mr,a=J/M是单位质量的角动量.

令Δ≡0,可得黑洞的视界半径为

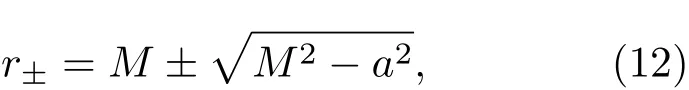
显然,引力彩虹Kerr黑洞的视界位置与经典Kerr黑洞的情况相同.

在经典Kerr黑洞中,黑洞温度为

而在引力彩虹时空中,温度可以修改为[58−60]

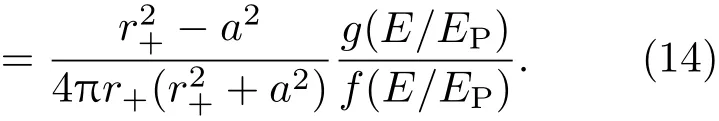
可以看出,黑洞的温度具有粒子能量依赖性,不同能量的粒子对黑洞的温度具有不同的有效描述.

接下来,计算粒子在引力彩虹Kerr黑洞视界上的隧穿作用量.考虑到Kerr黑洞中参考性的拖拽效应,视界附近的物质场会被引力场拖拽.这样,为了在Kerr黑洞中给出(6)式表示的绝热不变作用量,应采用拖拽坐标系.利用拖拽坐标变换

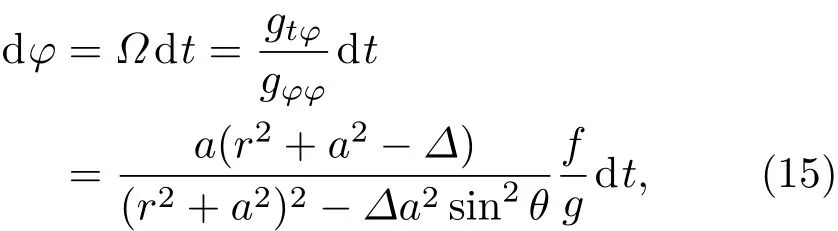
得到拖拽的引力彩虹Kerr黑洞线元为

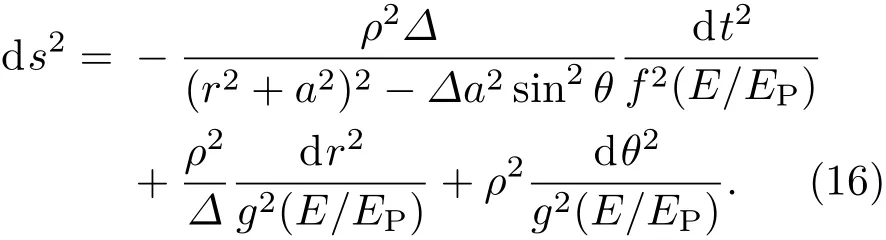
这其实是一个三维超曲面.而为了方便利用(6)式,变换t→iτ,其中i为虚数单位.可以得到(16)式对应的欧几里得线元

在拖拽坐标系中,坐标φ不再出现.这就是说,对于处于该转动时空中的物质-引力系统,坐标φ是一个可遗坐标[61,62].为了消除这一坐标对粒子隧穿的影响,绝热不变作用量(6)式应写为

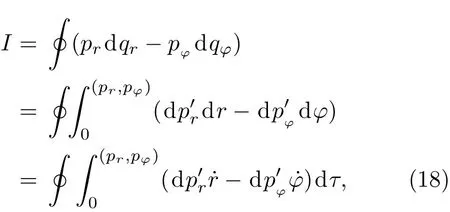
其中,pr和pφ为分别对应坐标r和φ的共轭动量,

为了对(18)式进行计算,利用哈密顿方程将动量用能量取代,

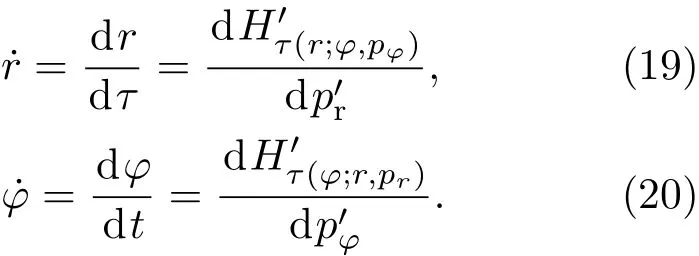
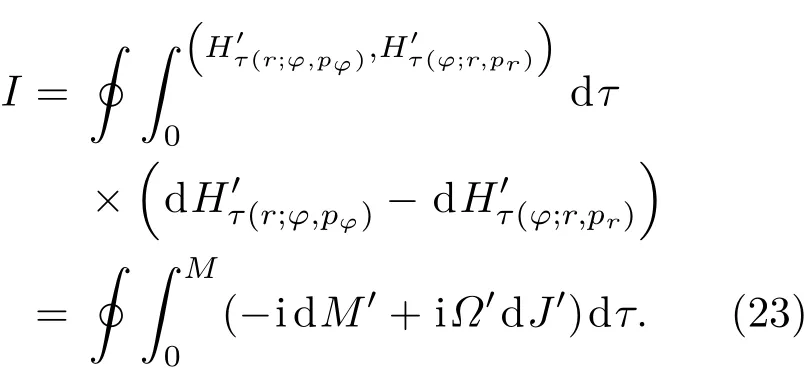
为了方便完成(23)式对时间的积分,可以利用事件视界的基本特征.考虑到在包含视界的环路上,欧几里得时间积分等于ħ乘以霍金温度的倒数[63],则有

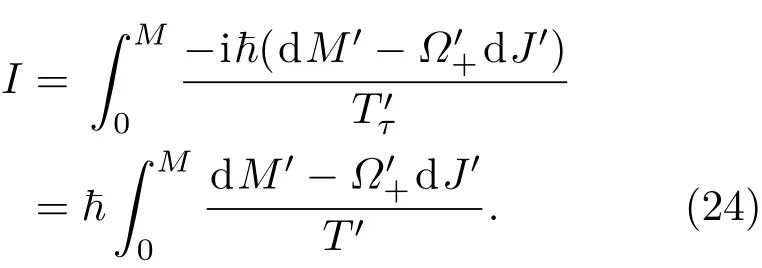
利用Kerr黑洞的热力学第一定律

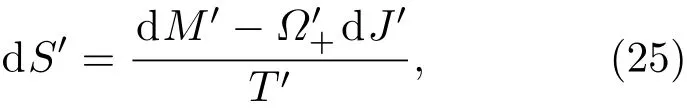
则(24)式变为

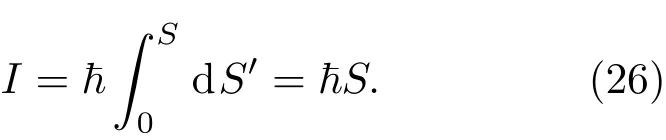
接下来,对(26)式表达的黑洞绝热不变作用量应用Bohr-Sommer field量子化规则

其中n=1,2,3,···.这样,就可以得到引力彩虹时空中Kerr黑洞的熵谱为

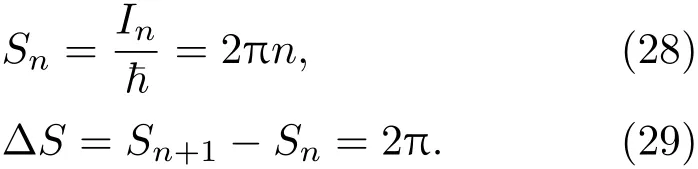
可以看出,在引力彩虹时空中,Kerr黑洞的熵谱是等间隔的,且与原始贝肯斯坦谱(1)式相同.而且,这里的结果也与应用Majhi和Vegenas的方法得到的其他黑洞的熵谱相同[27−32].尽管力彩虹时空本身是能量依赖的,但其中的Kerr黑洞熵谱独立于测试粒子的能量.

4 引力彩虹时空中Kerr黑洞的面积谱

黑洞的面积谱可以从熵谱和熵面积关系得到.如果使用(2)式的B-H公式,则根据(29)式的熵谱,可以得到面积谱

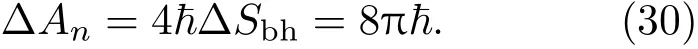
显然,这是与贝肯斯坦的原始结果(1)式相同的等间隔面积谱.当然这也与经典情况下的Kerr黑洞的结果相同.

然而,考虑到修改的色散关系的影响,引力彩虹时空中Kerr黑洞的熵面积关系应该具有对B-H熵的量子修正.这样,引力彩虹Kerr黑洞的面积谱也应该具有相应的来自时空量子效应的影响.接下来对此进行分析和讨论.

对于引力彩虹Kerr黑洞,注意到a=J/M,则(25)式的热力学第一定律可以写为

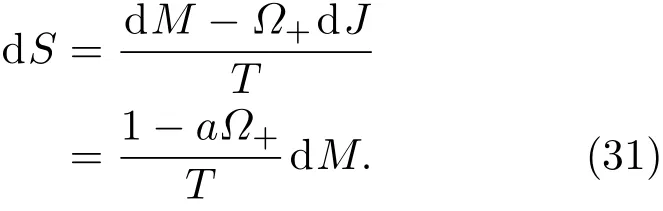
这里,考虑了黑洞辐射过程中保持角动量与质量比值不变的情况[61,62].而应用(10)式的修正的色散关系,黑洞温度可以表示为

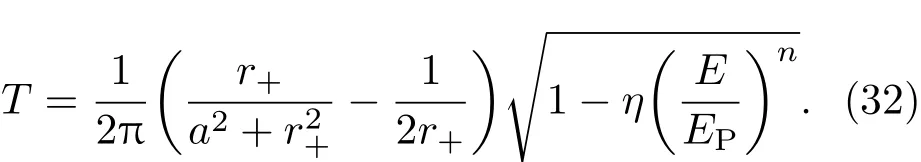
(32)式中,探测粒子的能量E可以等同于黑洞视界附近的粒子能量,而该能量可以从来自不确定原理的限制得到[64,65].考虑粒子的动量位置不确定原理Δp≥ ħ/Δx,则有粒子能量E≥ ħ/Δx.黑洞视界附近粒子的坐标不确定度由视界半径给出,且表示为Δx≈r+.这样就有辐射粒子的能量

黑洞视界附近的粒子形成了黑洞的霍金辐射,这就是说可以用黑洞的温度给出探测粒子的特征能量.对于Schwarzschild黑洞,A=4πr2+,则有

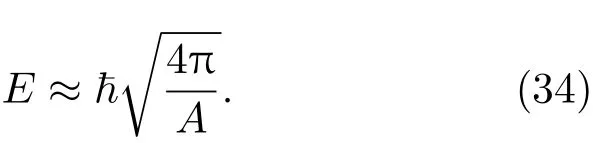
这里,作为对黑洞量子引力效应的一般性分析与讨论,对于Kerr黑洞,采用与Schwarzschild黑

洞一样的方式来给出探测粒子能量[66],且使用面积公式

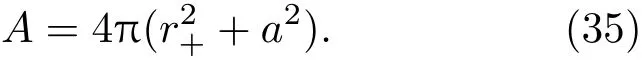
这样,引力彩虹Kerr黑洞的温度就可表示为

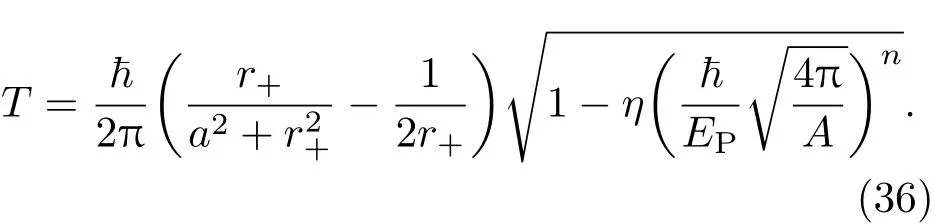
类似地,取视界上的角速度为

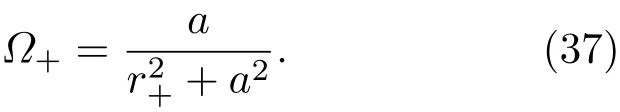
将(36),(37)式代入(31)式,可得

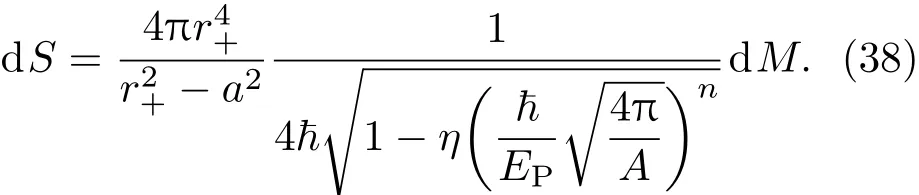
利用(12)式,并将辐射过程中黑洞单位质量的角动量视为常量,可得

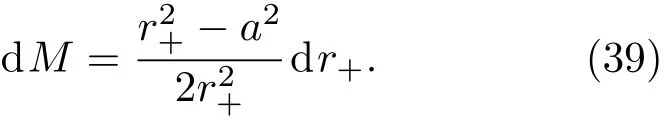
这样,将(39),(35)式代入(38)式,则有

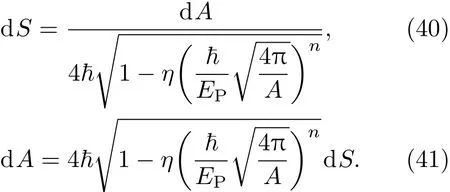
将(41)式与黑洞熵谱(29)式相结合,则有引力彩虹Kerr黑洞的面积谱

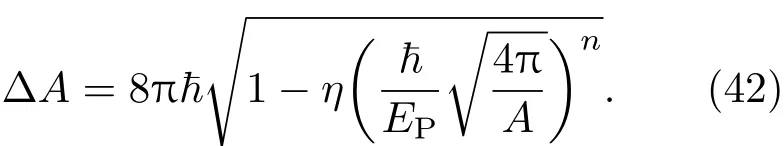
显然,这是与原始贝肯斯坦面积谱(1)式不同的非等间距谱,该面积谱是黑洞视界面积的函数.

从(42)式可以看出,随着黑洞面积的减小,面积间隔会变小,以面积谱的非等间距性和对面积的依赖性为特征的面积谱修正效应逐步明显.特别是随着黑洞的不断辐射,当黑洞的尺度达到普朗克量级,且当

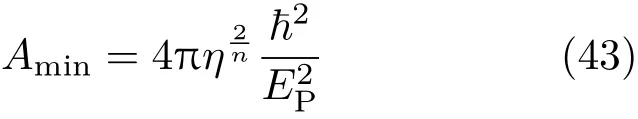
时,会有

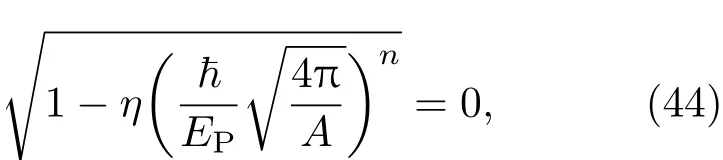
从而得到

此时面积间隔消失.但面积量子为零,并不意味着面积经典连续变化的出现,而是表明黑洞面积不再减小,黑洞达到了最小尺度.因为,从(43),(44)与(42)式可以看出,要求有物理意义的面积谱,则需要有A≥Amin,Amin是彩虹引力黑洞的最小面积.也就是说,黑洞面积达到Amin时,黑洞出现了辐射剩余.

另外,从(34)式可以看到,当A=Amin,有

这样,从(32)式可以看到,此时有黑洞温度

这表明黑洞辐射停止,剩余出现.这与利用量子引力效应对黑洞剩余的研究结果相一致[64−67].

不考虑色散关系的修正效应,当η→0时,从面积谱(42)式可以得到与原始贝肯斯坦面积谱(1)式一样的结果.另外,对于大黑洞,对(42)式做级数展开,可有

(48)式第一项即为贝肯斯坦面积谱(1)式的结果,第二、三项及以后各项为面积谱对贝肯斯坦面积谱的偏离和修正.这是与考虑量子修正效应的黑洞面积谱一致的结果[27].如果取n=2,则第一项修正为面积的倒数项,第二项修正为面积倒数的平方.修正项随着面积的增大而减少,在大黑洞极限下修正项可以忽略,从而面积谱(48)式可以回到贝肯斯坦面积谱.

可以看出,面积谱(42)式对贝肯斯坦面积谱的修改和偏离来自引力彩虹的量子效应.这样,这里修改的面积谱即为黑洞面积谱的量子修正,而且应与黑洞物理的其他量子效应相关,特别是应与黑洞熵的量子修正相一致.实际上,不考虑引力彩虹的量子效应,令η=0,从(40)式可以得到dS=dA/4ħ,从而得到(2)式的B-H熵,此时引力彩虹Kerr黑洞具有与经典Kerr黑洞一样的熵表达式,而此时的面积谱也与原始贝肯斯坦谱一样.考虑时空的量子效应,(40)式表示的熵面积关系就对B-H熵有偏离和修正.对(40)式做大黑洞展开,则有

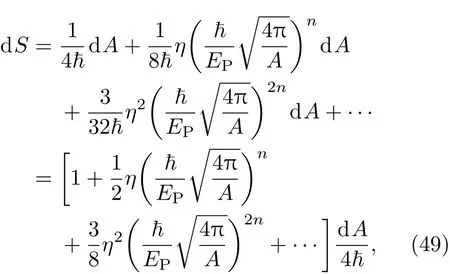
可以看出,对(49)式取零级近似并进行积分,即可得到B-H熵

对第二项和第三项积分,可得到黑洞熵量子修正的第二、三项为

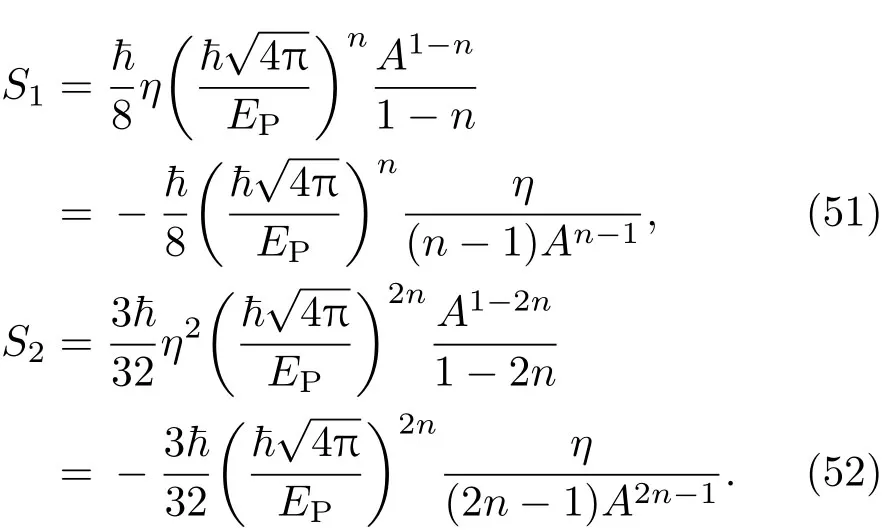
这样,就有引力彩虹Kerr黑洞的熵表达式

可以看出,黑洞熵的修正项来自引力彩虹时空的量子效应,且为黑洞面积的函数,但没有时空本身具有的粒子能量依赖性.令n=2,则第一项修正为面积的倒数项,第二项修正为面积倒数的三次方.随着面积的增大,修正项减小,而随着黑洞面积的减小,修正项增大.这是与(48)式的黑洞面积谱的量子修正一致的结果.实际上,黑洞熵与面积谱的修正均来自引力彩虹时空的量子效应,具有内在一致性.

给出黑洞的B-H熵及其量子修正是各种量子引力理论的一般要求和结果[68,69].人们希望量子引力理论不仅可以给出面积定律的理论解释,而且可以揭示黑洞熵量子修正的一般特征.通过一般的量纲分析,可以预期大黑洞有面积倒数幂律谱形式的对B-H熵的修正[68],从而有修正黑洞熵表达式

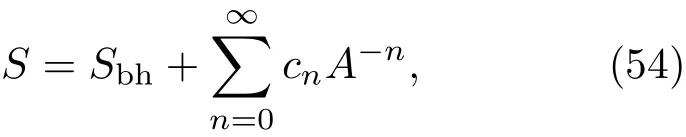
其中,系数cn不依赖于视界面积但与普朗克长度有关.而基于量子引力理论具体分析和黑洞量子性质的具体研究,给出的黑洞熵一般还具有面积的对数修正,且对数项为黑洞熵量子修正的主导项[58−60,68−72],从而有如下形式的量子修正熵:

其中,系数c0和cn与具体量子引力理论模式有关.比如,利用Cardy公式计算黑洞视界上的统计熵,在考虑量子修正的情况下,得到了多种黑洞的对数修正熵[70−72].利用修正色散关系,通过引力彩虹的Schwarzschild黑洞中的热力学分析,也可以给出黑洞熵的对数修正[58−60].

可以看出,这里给出的量子修正熵(53)式与(54)式的预期一致,但没有(55)式中的面积对数项.一般而言,黑洞熵的量子修正,在一定程度上与分析黑洞量子性质的具体理论和计算方法有关[58−60,68−72].但是,给出黑洞熵的面积对数修正项是黑洞熵量子修正的较普遍的研究结果.而且,在引力彩虹Schwarzschild黑洞中,也可以给出黑洞熵的面积对数项[58−60].这里,在引力彩虹的Kerr黑洞中,没有给出熵的对数修正,可能与本文采用的具体理论形式和计算处理有关.本文采用的(10)式表示的修正色散关系与文献[58—60]中的有所不同.修正色散关系的具体形式对黑洞熵修正项具体表达式的影响还需要做进一步分析.Kerr黑洞有比较复杂的结构,文中采用了(49)式的级数展开并做了分项积分,还采用了(34)和(35)式的不等式简化,相应的处理和计算结果在定量上还需要进一步讨论.

5 结果与讨论

将Majhi和Vegenas给出的通过绝热不变作用量研究黑洞光谱学的方法,应用到引力彩虹时空中的Kerr黑洞,研究了修正色散关系对转动黑洞熵谱和面积谱的影响.计算了引力彩虹Kerr黑洞的正则不变的作用量,并且对该作用量应用Bohr-Sommer field量子化规则,在不使用黑洞的准正则模的情况下,得到了引力彩虹时空中转动黑洞的熵谱.所得的熵谱(28)式是与原始的贝肯斯坦熵谱(3)式一样的等间距熵谱,这与经典Kerr黑洞和其他利用绝热不变的作用量在不同时空中得到的熵谱结果相同.而且,尽管引力彩虹Kerr黑洞是能量依赖的,但是熵谱独立于测试粒子的能量,这说明引力彩虹时空的量子效应,不影响转动黑洞的熵谱.这样,在说明黑洞熵谱的统一性方面,本文通过考察引力彩虹Kerr黑洞的情况提供了一个例证.

由于引力彩虹时空具有量子效应,得到的彩虹Kerr黑洞的面积谱(42)式与原始贝肯斯坦谱(3)式不同,是依赖于黑洞面积的不等间距谱,这是与通常的Kerr黑洞中的面积谱不同的结果.但当忽略修正色散关系效应时,面积谱(42)式可以回到普通黑洞的情况,并可以得到与原始贝肯斯坦谱一样的等间隔谱.另外,与黑洞熵谱相同,引力彩虹Kerr黑洞的面积谱也没有粒子能量依赖性.考虑时空的量子效应时,随着黑洞辐射的进行,黑洞的面积间隔将逐步变小.当黑洞达到普朗克尺度的最小面积时,面积量子变为零.最小面积是引力彩虹时空面积谱有物理意义的黑洞面积下限,从而说明了黑洞剩余的出现.同时,当黑洞面积最小时,有黑洞温度为零,引力彩虹黑洞将不再辐射粒子,说明黑洞出现具有最小面积的辐射剩余.而且,黑洞接近普朗克量级时,温度接近零,辐射粒子的能量也趋于零,面积的改变也就趋于零.这也说明黑洞剩余的存在,并且与其他利用引力的量子效应对黑洞辐射剩余的研究结果相一致.对引力彩虹Kerr黑洞的熵进行了讨论,得到了偏离B-H熵的修正黑洞熵,而且熵修正与面积谱的修正相对应和一致.黑洞面积谱和黑洞熵的修正项均与黑洞面积有关,且与面积的倒数成正比.黑洞面积谱与黑洞剩余的关系值得进一步研究.

[1]Bekenstein J D 1972Lett.Nuovo.Cim.4 737

[2]Bekenstein J D 1973Phys.Rev.D7 2333

[3]Bekenstein J D 1974Lett.Nuovo Cim.11 467

[4]Bekenstein J D 1998 arXiv:gr-qc/9808028

[5]Kunstatter G 2003Phys.Rev.Lett.90 161301

[6]Nollert H P 1999Class.Quant.Grav.16 R159

[7]Hod S 1998Phys.Rev.Lett.81 4293

[8]Hod S 1998Phys.Rev.D59 024014

[9]Maggiore M 2008Phys.Rev.Lett.100 141301

[10]Wang B,Lin C Y,Molina C 2004Phys.Rev.D70 064025

[11]Medved A J M 2008Class.Quantum Grav.25 205014

[12]Vagenas E C 2008JHEP2008 073

[13]Ropotenko K 2010Phys.Rev.D82 044037

[14]Kothawala D,Padmanabhan T,Sarkar S 2008Phys.Rev.D78 104018

[15]Wei S W,Li R,Liu Y X,Ren J R 2009JHEP2009 076

[16]Li W B,Xu L X,Lu J B 2009Phys.Lett.B676 177

[17]Jing J L,Ding C K 2008Chin.Phys.Lett.25 858

[18]Pan Q Y,Jing J L 2005Chin.Phys.B14 268

[19]Chen J H,Wang Y J 2010Chin.Phys.B19 060401

[20]Wei S W,Liu Y X,Yang K,Zhong Y 2010Phys.Rev.D81 104042

[21]Liu C Z 2012Eur.Phys.J.C72 2009

[22]Barvinsky A,Das S,Kunstatter G 2001Class.Quant.Grav.18 4845

[23]Barvinsky A,Das S,Kunstatter G 2002Found.Phys.32 1851

[24]Ropotenko K 2009Phys.Rev.D80 044022

[25]Kwon Y,Nam S 2010Class.Quant.Grav.27 125007

[26]Louko J,Makela J 1996Phys.Rev.D54 4982

[27]Majhi B R,Vagenas E C 2011Phys.Lett.B701 623

[28]Liu C Z 2012Chin.Phys.B21 070401

[29]Li L 2012Int.J.Ther.Phys.51 1924

[30]Liu C Z 2012Mod.Phys.Lett.A27 1250139

[31]Zeng X X,Liu W B 2012Eur.Phys.J.C72 1987

[32]Qi D J 2014Astrophys.Space.Sci.349 33

[33]Garay L J 1995Int.J.Mod.Phys.A10 145

[34]Gross D J,Mende P F 1988Nucl.Phys.B303 407

[35]Witten E 1997Phys.Today49 24

[36]Smolin L 2004 arXiv:hep-th.0408048

[37]Ali A F,Faizal M,Khalil M M 2014JHEP2014 159

[38]Ali A F,Faizal M,Khalil M M 2015Phys.Lett.B743 295

[39]Gangopadhyay S,Dutta A,Saha A 2014Gen.Rel.Grav.46 1661

[40]Dutta A,Gangopadhyay S 2014Gen.Rel.Grav.46 1747

[41]Gangopadhyay S,Dutta A,Faizal M 2015Euro.Phys.Lett.112 20006

[42]Dutta A,Gangopadhyay S 2016Int.J.Theo.Phys.55 2746

[43]Ma H,Li J 2017Chin.Phys.B26 60401

[44]Chen N S,Zhang J Y 2015Chin.Phys.B24 020401

[45]Ibungochouba S T 2015Chin.Phys.B24 70401

[46]Ye B B,Chen J H,Wang Y J 2017Chin.Phys.B26 90202

[47]Amelino-Camelia G 2002Int.J.Mod.Phys.D11 35

[48]Amelino-Camelia G 2001Phys.Lett.B510 255

[49]Kowalski-Glikman J 2001Phys.Lett.A286 391

[50]Magueijo J,Smolin L 2002Phys.Rev.Lett.88 190403

[51]Magueijo J,Smolin L 2003Phys.Rev.D67 044017

[52]Kimberly D,Magueijo J,Medeiros J 2004Phys.Rev.D70 084007

[53]Magueijo J,Smolin L 2004Class.Quant.Grav.21 1725

[54]Heuson C 2006 arXiv:gr-qc/0606124

[55]Amelino-Camalia G,Ellis N E,Mavromatos D V 1997Int.J.Mod.Phys.A12 607

[56]Amelino-Camalia G 2013Living.Rev.Rel.16 5

[57]Altamirano N,Kubiznak D,Mann R B,Sherkatghanad Z 2014Galaxies2 89

[58]Ling Y,Li X,Hu B 2007Mod.Phys.Lett.A22 2749

[59]Ling Y,Hu B,Li X 2006Phys.Rev.D73 087702

[60]Liu C Z,Zhu J Y 2008Gen.Relat.Gravit.40 1899

[61]Zhang J Y,Zhao Z 2005Mod.Phys.Lett.A20 1673

[62]Jiang Q Q,Wu S Q,Cai X 2006Phys.Rev.D73 064003

[63]Gibbons G W,Hawking S W 1977Phys.Rev.D15 2752

[64]Adler R J,Chen P,Santiago D I 2001Gen.Rel.Grav.33 2101

[65]Amelino-Camelia G,Arzano M,Procaccini A 2004Phys.Rev.D70 107501

[66]Ali A F,Mohammed M F,Khalil M 2015Nucl.Phys.B894 341

[67]Ali A F 2014Phys.Rev.D89 104040

[68]Kaul R K,Majumder P 2000Phys.Rev.Lett.84 5255

[69]Don N 2005Page,New.J.Phys.7 203

[70]Jing J L,Yan M L 1999Phys.Rev.D60 084015

[71]Carlip S 2000Class.Quant.Grav.17 4175

[72]Jing J L,Yan M L 2000Phys.Rev.D63 024003