利用衍射光栅探测涡旋光束轨道角动量态的研究进展∗

付时尧 高春清

(北京理工大学光电学院,北京 100081)

1 引 言

涡旋光束一般指相位涡旋光束[1,2],具有螺旋形波前,光束中心存在相位奇点,光强分布为环形.早在1992年荷兰莱顿大学的Allen等[2]就指出复振幅表达式中含有相位项exp(ilφ)的光束具有轨道角动量(orbital angular momentum,OAM),其中,l为角量子数或拓扑荷,φ为角向坐标.涡旋光束所包含的每一个光子均携带有OAM值为lħ,即参数l决定了涡旋光束所携带的OAM大小,是涡旋光束的特征值,因此l也被称为OAM态.常见的涡旋光束有拉盖尔-高斯光束[2]、贝塞尔及贝塞尔-高斯光束[3,4]、超几何高斯光束[5]等.涡旋光束携带有OAM的性质,使得其在粒子俘获与操纵[6]、矢量光束的生成[7−9]、光通信[10−13]、涡流探测[14,15]、旋转探测[16,17]等领域有着广泛的应用.在各种应用中,确定涡旋光束的OAM态非常重要.

当前涡旋光束OAM态的主要探测手段有干涉法[18−23]、多普勒分析法[24]、超材料表面法[25−27]以及衍射光栅法[28−36,40−60]等.干涉法即通过引入一参考光束,将参考光束与涡旋光束干涉,通过观察干涉条纹的形态来判断涡旋光束的OAM态[18−20].亦可利用Mach-Zehnder干涉仪来分离具有不同奇偶性角量子数的涡旋光束,实现OAM态的测量[21−23].多普勒分析法则基于旋转多普勒效应,由于具有螺旋波前的涡旋光束,其横向的旋转等效为纵向的平移,因此光束的旋转也将等效为光束的频移[24].若光束旋转角频率为Ω,光束角量子数为l,则光束产生频移lΩ/(2π),因此,若测出频移,则可测得OAM态.超材料表面一般采用微纳加工的方式,在硅基或其他半导体表面上进行特殊加工,当涡旋光束照射该超材料表面时,其衍射光场会呈现出与其携带的OAM相关的特殊形态,通过判断该形态即可确定待测光束所携带的OAM[25−27].衍射光栅法即设计特殊的衍射光栅,通过观察涡旋光束的远场衍射形态来判断其携带的OAM.相比于其他几种方法,衍射光栅由于制备简单,操作方便,故在OAM态的探测领域应用较广.本文主要回顾近年来利用衍射光栅探测涡旋光束OAM态研究的国内外进展.

2 单一模式涡旋光束的探测

涡旋光束经过衍射光栅时,会出现与传统高斯光束不同的特点.2006年,纽约城市大学Sztul和Alfano[28]进行了涡旋光束的杨氏双缝干涉实验,发现可利用杨氏双缝干涉来测量涡旋光束的OAM.与传统的高斯光束的杨氏双缝干涉实验不同,对于涡旋光束,由于其具有螺旋形相位,在x,y两个方向上均存在相位梯度,因此涡旋光束的双缝干涉条纹出现由y方向相位差引起的错位.他们分别用±1阶涡旋光束和普通平面波进行双缝实验,实验结果如图1所示.可以看出,对于涡旋光束,除了产生干涉条纹错位外,错位方向与角量子数的符号有关,其原因在于具有相反角量子数的涡旋光束,经双缝透过的相位差沿着y轴的梯度方向不同.

图1 实验测得的干涉条纹(a)−1阶涡旋光束;(b)平面波;(c)+1阶涡旋光束[28]Fig.1.Interferential results:(a)−1st order vortices;(b)0th order vortices;(c)+1st order vortices[28].

2014年,Emile等[29]实验研究了高阶涡旋光束通过双缝衍射后的条纹特性,他们发现条纹的错位与入射光束的角量子数的绝对值相同,即角量子数的绝对值越大,条纹的移动量越大.

图2 不同阶次(本图中以符号m表示)的涡旋光束经三角孔衍射后的理论仿真与实验结果[30]Fig.2.Simulated and experimental results when optical vortices with different topological charges m passing through a triangular aperture[30].

与双缝衍射类似,三角形孔也可以用来测量涡旋光束的OAM态[30−32].Hickmann等[30,31]报道了一种通过三角形孔来实现涡旋光束探测的方案.涡旋光束经三角孔后,其远场衍射呈现特殊的三角形光斑阵列,光斑阵列的排列方向决定了角量子数的正负,光斑阵列里的光斑个数则与角量子数的绝对值相关,即通过远场光束阵列的光斑个数和光斑排列方向,可以确定入射涡旋光束的OAM态.Hickmann等[30]分别生成了+1阶、+2阶和+3阶涡旋光束,它们经过三角孔后的远场衍射光斑的理论仿真结果和实验结果如图2所示.可以看出,当涡旋光束经过三角孔衍射时,远场衍射光斑也呈三角形分布,且其每一边的光斑数减1即为入射光束角量子数的绝对值.Hickmann等[30]也仿真分析了具有相反符号的角量子数的涡旋光束经三角孔后的衍射,发现它们的衍射光斑排列方向相反.

2011年,Liu等[33]在Hickmann等的研究基础上,提出了一种用三角形环形缝(三角缝)来实现涡旋光束探测的方案,可以得到比传统的三角孔更清晰的衍射结果,并通过实验进行了验证.Liu等[33]还分别研究了不同缝宽对探测结果的影响,其中缝宽由三角缝内外边长的比率η表征,发现η越大,远场衍射光阵列越清晰.

2013年,Liu等[34]提出了一种利用角向双缝来探测涡旋光束的方案.后来,Fu等[35]又在此基础上开发了动态角向双缝测量法.与杨氏双缝类似,角向双缝也是利用了两个缝所透过的涡旋光束相位不同的原理,可根据干涉条纹的形态来确定入射光束的OAM态.另外,角向双缝探测法对非整数OAM态的测量同样有效[36].

前面介绍的方法,均是利用缝或者孔类的振幅光栅进行涡旋光束的探测,然而它们需要使衍射光学器件的中心与被测光束的中心重合,另外衍射器件的结构和尺寸对测量结果也有影响.为了使涡旋光束的测量方法更加简便,可借助常见的光学透镜来实现.

柱面镜是一种非球面透镜,具有一维放大的功能.早在1993年,Beijersbergen等[37]就提出了一种由两个柱面镜组成的模式转换器,将高阶厄米-高斯光束转化为涡旋光束.本课题组于2001年利用三个柱面镜组成的模式转换器生成了高阶拉盖尔-高斯光束[38],并利用生成的涡旋光束研制了光学扳手来实现对微米尺度的粒子的旋转[39].由于光路的可逆性,上述方案也可以逆过来探测涡旋光束.当涡旋光束通过柱面镜时,通过柱面镜的后焦面的光斑数及其排布方向即可获得待测光束的角量子数[40−43].另外,该方法对脉冲光[40]和非单色光[42]同样有效.2016年,美国Alperin等[43]提出了一种用柱面镜来定量分析涡旋光束的角量子数的方法,该方法也适用于非整数角量子数的情况.他们利用电荷耦合器件(CCD)相机来接收柱面镜后焦面上的光斑,而后通过计算柱面镜后焦面光斑两个坐标方向的协方差,进而算得角量子数l.柱面镜测量OAM态实际可理解为在x和y两个方向上对光场引入了不同的傅里叶变换,与此类似,采用倾斜放置的透镜也可实现涡旋光束的定性探测[44,45].

下面介绍通过设计特殊的光栅来实现涡旋光束的探测.2015年本课题组提出了一种如图3所示的周期渐变光栅[46].

当不同阶次的涡旋光束入射时,其远场衍射会表现出不同的形态.根据远场衍射光斑的形态,就可以确定入射涡旋光束的OAM态.以一级衍射为例,首先,当入射涡旋光束的角量子数为正时,一级衍射光斑呈纵向排列,当入射涡旋光束的角量子数为负时,一级衍射光斑呈横向排列.也就是说,通过观察远场衍射中一级衍射光斑的排列情况,可确定入射涡旋光束的角量子数的正负.其次,一级衍射光斑的节线数,亦可理解为一级衍射中的小光斑数减1,为角量子数的绝对值.在实验中,可通过打印机直接将光栅打印在高透相纸上,如图4(a)所示.实验测得的周期渐变光栅的远场衍射如图4(b)所示.

图3 周期渐变光栅[46]Fig.3.Gradually-changing-period grating[46].

在文献[46]的基础上,科研人员又提出了周期渐变型衍射光学器件[47,48],使得衍射效率大大提高.特别是本课题组的工作[48]中,实现了径向量子数不为0的拉盖尔-高斯型涡旋光束的探测,如图5所示.

与其他利用衍射方法检测OAM态的方法相比,周期渐变光栅的主要优点为光路准直要求低,当入射涡旋光束偏离周期渐变光栅中心时,衍射光场并不影响OAM态阶数的判断[46].周期渐变光栅虽使用方便,但仍存在一定的局限性,它无法实现多模复用涡旋光束的检测.

图4(a)实验所用周期渐变光栅;(b)不同阶次涡旋光束入射时,远场衍射的实验结果[46]Fig.4.(a)The gradually-changing-period grating employed in the experiment;(b)far- field diffractions when the incident optical vortice has various topological charges[46].

图5 文献[48]中的周期渐变型衍射光学器件可实现多环结构拉盖尔高斯型涡旋光束(径向量子数非零)的探测Fig.5.Detection of multi-ring optical vortices through the gradually-changing-period diffraction element[48].

图6 使用环形光栅探测涡旋光束的技术方案[49]Fig.6.Detecting optical vortices by using annular gratings[49].

2017年,华中科技大学Zheng等[49]提出了一种利用环形光栅来探测涡旋光束的方案,如图6所示.当涡旋光束经过环形光栅时,会产生与文献[46,47]相似的实验结果,其OAM态的判断方法也与文献[46,47]相同.同时,相位型环形光栅的衍射效率明显比振幅型高.

3 多模混合涡旋光束的探测

上节介绍的探测方法中,对单一模式的涡旋光束十分有效,但其对多模混合涡旋光束无能为力.下面介绍的复合振幅光栅[50,51]可以很好地解决这一问题.

复合叉状光栅将两个不同方向的叉形光栅复合在一起,如图7所示,当一束高斯光束通过复合叉状光栅时,其远场衍射将会是一光斑阵列.若一束涡旋光束通过复合叉状光栅时,其远场的光束阵列中必然会出现实心光斑,通过实心光斑出现的衍射级的位置,即可确定入射光束的OAM态[52].若入射光束为多模混合涡旋光束,则远场衍射会出现多个实心光斑,根据这些实心光斑出现的位置,可确定入射光束的OAM态分布.

2009年,Moreno等[53]提出了一种新的衍射光栅,通过改变二值化相位光栅周期相位分布,可将−3至+3多个衍射级同时显现,通过设计不同的叉形,可实现涡旋光束的探测,其探测原理与文献[50–52]相似.由于上述几种光栅虽可探测多模复用涡旋光束,但它们OAM态的连续可探测范围普遍偏低(例如,在文献[50–52]中,OAM 态的连续可探测范围为−4–+4).2010年,Zhang等[54]提出了一种新型的达曼涡旋光栅,其远场衍射为一5×5涡旋光束阵列,可将OAM态的连续可探测范围拓展至−12–+12.

图7 复合叉状光栅(a)普通叉状相位光栅及其远场衍射;(b)二值化后的横向相位光栅及其远场衍射;(c)二值化后的纵向相位光栅及其远场衍射;(d)复合叉状光栅及其远场衍射[51]Fig.7.Composite fork gratings:(a)Fork phase grating and its far- field diffraction;(b)binary fork grating in x-direction and its far- field diffraction;(c)binary fork grating in y-direction and its far- field diffraction;(d)binary composite fork grating and its far- field diffraction[51].

由于−12–+12的探测范围仍无法满足部分应用如光通信等的应用要求,2016年,本课题组提出了一种整合达曼涡旋光栅,将多模混合OAM态的探测范围拓展至−24–+24[55].文献[55]中,将5×5二维达曼涡旋光栅与±12阶螺旋相位片相结合使达曼涡旋光栅可检测的光束的OAM态增加或减少12,从而将达曼涡旋光栅的探测范围拓展至−24–+24.±12阶螺旋相位片与5×5二维达曼涡旋光栅的整合过程如图8所示,其中图8(d)和图8(e)为整合后的达曼光栅.

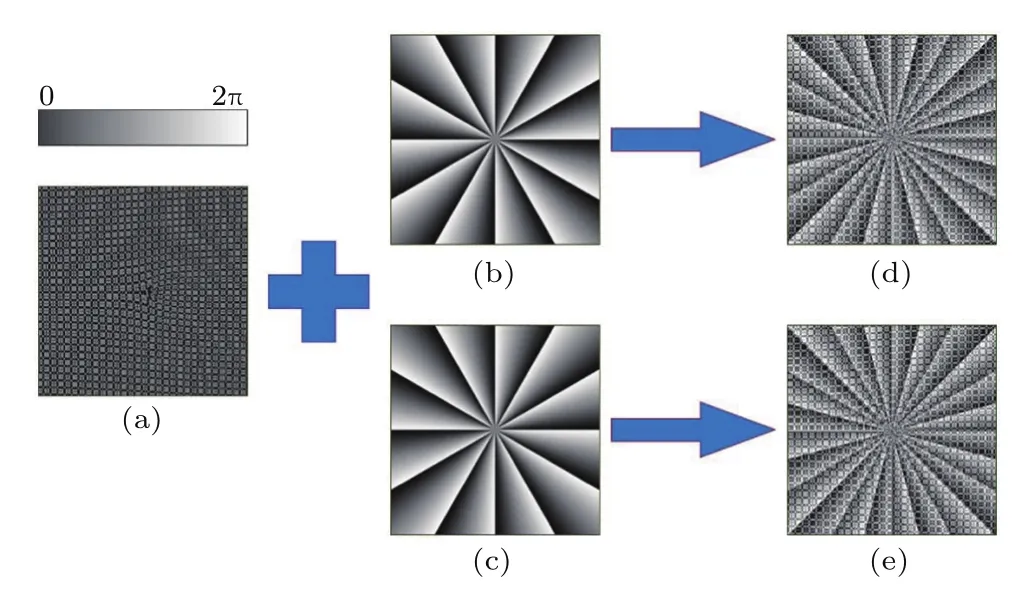
图8 ±12阶螺旋相位片与5×5二维达曼涡旋光栅的结合过程(a)5×5二维达曼涡旋光栅;(b)+12阶螺旋相位片;(c)−12阶螺旋相位片;(d)+12阶整合后的达曼涡旋光栅;(e)−12阶整合后的达曼涡旋光栅[55]Fig.8.Diagrams of integrating a 5×5 two-dimensional Dammann vortex grating with a+12th or−12th order spiral phase plate:(a)5×5 two-dimensional Dammann vortex grating;(b)+12th order spiral phase plate;(c)−12th order spiral phase plate;(d)the grating that results from integrating(a)and(b);(e)the grating that results from integrating(a)and(c)[55].

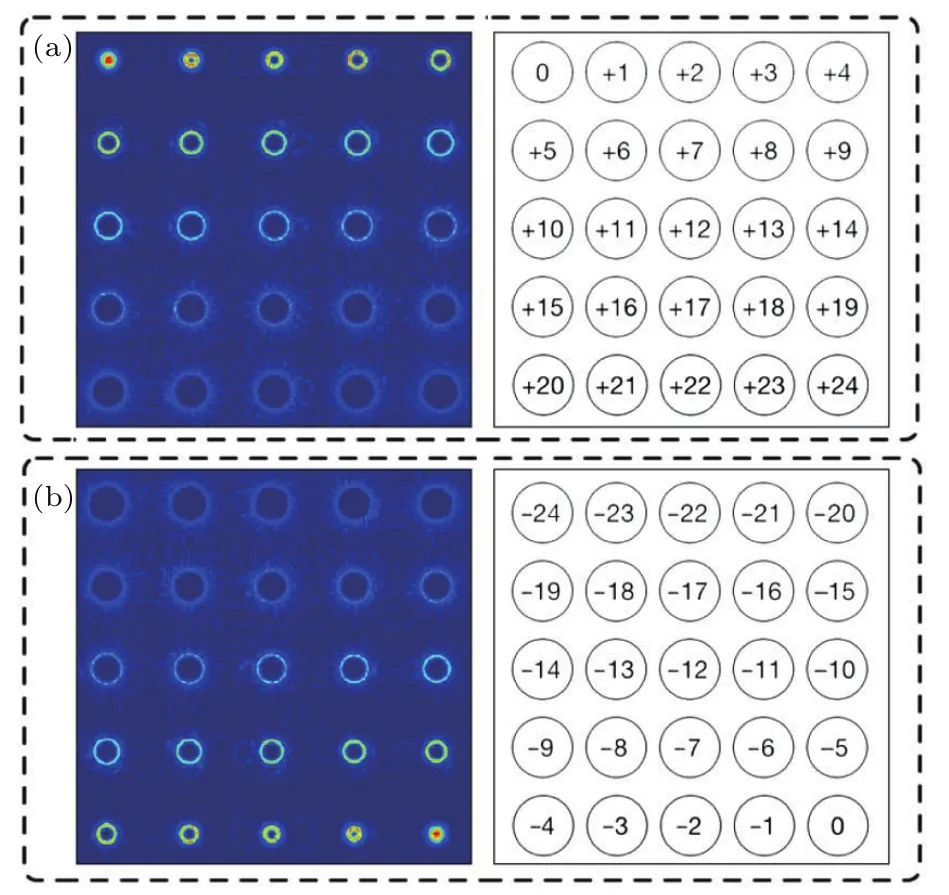
图9 高斯光束通过整合达曼涡旋光栅后的远场衍射光场及其OAM态分布(a)和(b)分别为高斯光束照射图8(d)和图8(e)时的远场衍射情形[55]Fig.9.Simulation results of the far- field diffraction patterns and OAM state distributions when Gaussian beams propagate through the integrated Dammann gratings:(a)and(b)are the simulated far- field diffraction patterns and the OAM state distributions when using the grating shown in Fig.8(d)and 8(e)respectively[55].

当一束高斯光入射到加载了上述整合达曼光栅(图8(d))的空间光调制器上后,远场衍射图样为一5×5的涡旋光束阵列.阵列中所有光斑的能量均相同,OAM态从左上至右下分别为0–+24,如图9(a)所示.同样,若使用图8(e)所示的整合达曼光栅,则得到的远场衍射的涡旋光束阵列的OAM态分布从左上至右下分别为−24–0,如图9(b)所示.如果采用涡旋光束照射整合达曼涡旋光栅,则其远场衍射也会是一个5×5的涡旋光束阵列,但其OAM态的分布会发生变化.通过观测远场衍射光阵列中实心光斑出现的位置,可以反推出入射涡旋光束的OAM态.当多模复用涡旋光束入射时,会出现多个实心光斑,因此可确定其所含有的OAM成分.

4 涡旋光束OAM谱的测量

OAM谱定义为光束在其所携带的不同OAM上的能量比率,可以反映光束的OAM的一些性质,是评价涡旋光束的重要参数之一.对于多模混合涡旋光束,OAM成分相同但其所占的比重不同时,其强度分布、波前分布等性质是不同的.因此当探测多模混合涡旋光束时,除了确定其所包含的角量子数或OAM成分外,还应明确各个成分间的能量比率,即OAM谱.

2010年,Berkhout等[56]提出了一种可有效分离光束不同OAM模式的方法.他们采用几何变换的方式,通过衍射光栅将涡旋光束的环形结构展开,由于展开后不同的OAM模式具有不同的相位梯度,因此经透镜聚焦后即可将不同的OAM成分聚焦在后焦面不同的位置处,实现了不同OAM成分的分离,如图10所示.后来,Lavery等[57]又在此基础上分别测出分离开的各个OAM分量的强度,得到了OAM谱.另外,他们也用聚甲基丙烯酸甲酯等材料直接将分束光栅加工出来,以便于在小型化系统中的应用[58].而Mirhosseini等[59]则对这一方法进行了优化,使得OAM谱的探测精度更高.

图10 OAM模式分束器[57]Fig.10.OAM mode sorter[57].

本课题组于2016年提出了一种灰阶算法[60],用来分析涡旋光束经文献[54]给出的达曼涡旋光栅后的衍射光场,并能够直接输出入射涡旋光束的OAM谱.当涡旋光束照射达曼涡旋光栅时,若衍射光场的某位置处的光斑的中心出现实心亮斑,表明入射光束携带与该位置相反的OAM.另外,光斑中心出现的实心亮斑完全由入射光束中角量子数为相应衍射级次的相反数的分量转化而来,若测出实心亮斑的光强,即可得到该OAM分量在入射光束中的比例.依次测出所有分量的光强,即可测得入射光束的OAM谱.理论上,达曼涡旋光栅的远场衍射光场的25个光斑的光强比是相同的[54],因此只需按上述方法依次分析25个衍射光斑,通过计算即可得到入射光束的OAM谱.

对于面阵探测器接收到的达曼涡旋光栅的衍射光场而言,在不超过其阈值的前提下,接收到的光斑的每个像素的灰度值的和与该光束的光强成正比,故可用灰度来表征光强.依次读取位于每一个衍射级处子光斑的每一个像素点的灰度值,并对灰度值求和,则可得到各衍射级的强度之比.由于这里没有用到任何光功率测量器件,而仅仅分析了面阵探测器接收到衍射场的灰度分布,因此我们将这种分析OAM谱的方法称为灰阶算法.灰阶算法测OAM谱的思路是:首先从头到尾依次扫描每一个衍射级的光斑,并在扫描的过程中确定不同衍射级是否存在中心亮斑,以此来判断入射涡旋光束是否存在该位置表征的OAM.若不存在,则继续扫描下一个光斑,若存在则计算中心亮斑的光强(即灰值的和).当所有光斑都处理完之后,可获得不同模式的能量比例,即入射涡旋光束的OAM谱.

图11 灰阶算法测量OAM谱的实验结果[60]Fig.11.Experimental results of measuring OAM spectra through gray-scale algorithm[60].

图11给出了一组实验结果,为四路涡旋光束复用时的情况.由于CCD存在一定的噪声,因此在分析的过程中,设定当中心归一化灰度值(1表示白,0表示黑)大于0.098时,表示该位置存在实心光斑.另外,受实际操作环境等多方面因素影响,达曼涡旋光栅衍射场中的25个光斑的光强并不是严格的相同.在实际测量前需先测出各衍射级次的能量比例分布,而后对OAM谱的测量结果进行补偿.可以看出,未经补偿时,实验结果与理论结果相差较大,经过补偿后,实验值与理论值符合完好.

5 总结与展望

涡旋光束作为一种新型的携带有OAM的结构光束,在光通信、光镊等诸多领域具有重要的应用价值.随着人们对涡旋光束研究的不断深入,越来越多的基于涡旋光束的新应用、新技术被不断发掘出来.本文较为系统地介绍了利用衍射光栅来测量涡旋光束OAM态的国内外进展,它们均可方便地测出涡旋光束的OAM态,为涡旋光束的实际应用提供了重要基础.然而,这些工作的探测方法所涉及的OAM态的绝对值|l|均较小(|l|为10的量级),虽然理论上它们对于较大角量子数(如|l|＞100)的涡旋光束同样有效,但面阵探测器的分辨率不够高等问题均给实际的探测带来一定的困难,因此如何方便地探测大|l|数的涡旋光束的OAM态仍是需解决的问题.

[1]Yao A M,Padgett M J 2011Adv.Opt.Photon.3 161

[2]Allen L,Beijersbergen M W,Spreeuw R J C,et al.1992Phys.Rev.A45 8185

[3]Volke-Sepulveda K,Garcés-Chávez V,Chávez-Cerda S,et al.2002J.Opt.B,Quantum Semiclass.Opt.4 S82

[4]Vasara A,Turunen J,Friberg A T 1989J.Opt.Soc.Am.A6 1748

[5]Kotlyar V V,Skidanov R V,Khonina S N,Soifer V A 2007Opt.Lett.32 742

[6]Amos B,Gill P 1995Meas.Sci.Technol.6 248

[7]Fu S,Gao C,Shi Y,et al.2015Opt.Lett.40 1775

[8]Liu S,Li P,Peng T,Zhao J 2012Opt.Express20 21715

[9]Fu S,Zhang S,Gao C 2016Sci.Rep.6 30765

[10]Wang J,Yang J Y,Fazal I M,et al.2012Nat.Photon.6 488

[11]Bozinovic N,Yue Y,Ren Y,et al.2013Science340 1545

[12]Willner A E,Huang H,Yan Y,et al.2015Adv.Opt.Photon.7 66

[13]Yu S 2015Opt.Express23 3075

[14]Belmonte A,Rosales-Guzman C,Torres J P 2015Optica2 1002

[15]Ryabtsev A,Pouya S,Safaripour A,et al.2016Opt.Express24 11762

[16]Lavery M P J,Speirits F C,Barnett S M,et al.2013Science341 537

[17]Fu S,Wang T,Zhang Z,Zhai Y,Gao C 2017Opt.Express25 20098

[18]Basistiy I V,Bazhenov V,Soskin M S,et al.1993Opt.Commun.103 422

[19]Harris M,Hill C,Tapster P,et al.1994Phys.Rev.A49 3119

[20]Soskin M,Gorshkov V,Vasnetsov M,et al.1997Phys.Rev.A56 4064

[21]Leach J,Padgett M J,Barnett S M,et al.2002Phys.Rev.Lett.88 257901

[22]Wei H,Xue X,Leach J,Padgett M J,et al.2003Opt.Commun.223 117

[23]Leach J,Courtial J,Skeldon K,et al.2004Phys.Rev.Lett.92 013601

[24]Vasnetsov M V,Torres J P,Petrov D V,et al.2003Opt.Lett.28 2285

[25]Yu N,Capasso F 2014Nat.Mater.13 139

[26]Jin J,Luo J,Zhang X,et al.2016Sci.Rep.6 24286

[27]Liu J,Min C,Lei T,et al.2016Opt.Express24 212

[28]Sztul H I,Alfano R R 2006Opt.Lett.31 999

[29]Emile O,Emile J 2014Appl.Phys.B117 487

[30]Hickmann J M,Fonseca E J,Soares W C,et al.2010Phys.Rev.Lett.105 053904

[31]Soares W C,Vidal I,Caetano D P,Fonseca E J,Chávez-Cerda S,Hickmann J M 2008 Frontiers in Optics Rochester,New York,United States,October 19–23,2008 pFThO2

[32]Stahl C,Gbur G 2016 J.Opt.Soc.Am.A 33 1175

[33]Liu Y,Tao H,Pu J,et al.2011 Opt.Laser Technol.43 1233

[34]Liu R,Long J,Wang F,et al.2013 J.Opt.15 125712

[35]Fu D,Chen D,Liu R,et al.2015 Opt.Lett.40 788

[36]Zhu J,Zhang P,Fu D,et al.2016 Photon.Res.4 187

[37]Beijersbergen M W,Allen L,van der Veen H E L O,Woerdman J P 1993 Opt.Commun.96 123

[38]Gao C,Wei G,Weber H 2001 Chin.Phys.Lett.18 771

[39]Gao M W,Gao C Q,He X Y,et al.2004 Acta Phys.Sin.53 413(in Chinese)[高明伟,高春清,何晓燕,等 2004物理学报53 413]

[40]Serna J,Encinas-Sanz F,Neme G 2001 J.Opt.Soc.Am.A 18 1726

[41]Denisenko V G,Soskin M S,Vasnetsov M V 2002 Proc.SPIE 4607 54

[42]Denisenko V,Shvedov V,Desyatnikov A S,Neshev D N,Krolikowski W,Volyar A,Soskin M,Kivshar Y S 2009 Opt.Express 17 23374

[43]Alperin S N,Niederriter R D,Gopinath J T,et al.2016 Opt.Lett.41 5019

[44]Vaity P,Banerji J,Singh R P 2013 Phys.Lett.A 377 1154

[45]Chaitanya N A,Jabir M V,Samanta G K 2016 Opt.Lett.41 1348

[46]Dai K,Gao C,Zhong L,et al.2015 Opt.Lett.40 562

[47]Li Y,Deng J,Li J,et al.2016 IEEE Photon.J.8 7902306

[48]Fu S,Wang T,Gao Y,Gao C 2016 Chin.Opt.Lett.14 080501

[49]Zheng S,Wang J 2017 Sci.Rep.7 40781

[50]Gibson G,Courtial J,Barnett S,et al.2004 Proc.SPIE 5550 p367

[51]Gibson G,Courtial J,Padgett M,et al.2004 Opt.Express 12 5448

[52]Xin J T 2013 Ph.D.Dissertation(Beijing:Beijing Institute of Technology)(in Chinese)[辛璟焘 2013博士学位论文(北京:北京理工大学)]

[53]Moreno I,Davis J A,Pascoguin B M,et al.2009 Opt.Lett.34 2927

[54]Zhang N,Burge R E,Yuan X C 2010 Opt.Lett.35 3495

[55]Fu S,Wang T,Zhang S,Gao C 2016 Appl.Opt.55 1514

[56]Berkhout G C,Lavery M P J,Courtial J,et al.2010 Phys.Rev.Lett.105 153601

[57]Lavery M P J,Berkhout G C G,Courtial J,et al.2011 J.Opt.13 064006

[58]Lavery M P J,Robertson D J,Berkhout G C G,et al.2012 Opt.Express 20 2110

[59]Mirhosseini M,Malik M,Shi Z,et al.2013 Nat.Commun.4 2781

[60]Fu S,Zhang S,Wang T,Gao C 2016 Opt.Express 24 6240