凹槽铜基底表面与单层石墨烯的相互作用特性研究∗

张忠强 贾毓瑕 郭新峰 葛道晗 程广贵 丁建宁2)

1)(江苏大学微纳米科学技术研究中心,镇江 212013)

2)(常州大学,江苏省光伏科学与工程协同创新中心,常州 213164)

3)(大连理工大学,工业装备结构分析国家重点实验室,大连 116024)

1 引 言

石墨烯作为一种二维材料,因为其在基础科学、纳米电子、生物和纳米机械等领域具有很多迷人的特性,近年来备受关注[1−4].石墨烯的制备方法主要有:微机械剥离法[5]、外延生长法[6]、氧化还原法[7]、化学气相沉积(chemical vapor deposition,CVD)法[8]等.目前,基于金属催化剂为基底的CVD法生长石墨烯薄膜[9]是非常具有前景的合成方法,然而,制备出高质量的石墨烯只是石墨烯合成上的发展与进步,要实现石墨烯的产业化应用主要还是取决于大面积薄膜转移技术的突破[10].这是因为在将石墨烯应用于器件时,需要将其转移至与器件相匹配的目标基底上,由此得到的石墨烯的优劣将影响器件的最终性能,然而大面积石墨烯与目标基底之间的相互作用大多都是未知的.因此,石墨烯的发展前景与其转移技术的发展是密不可分的.同时,由悬浮石墨烯构成的纳米谐振器也具有非常优异的性能,如厚度薄、比表面积大、高灵敏度以及共振率高等[11],而对于高质量的石墨烯谐振器,石墨烯和基底之间的相互作用是一个很重要的问题,认识和描述基底上石墨烯膜的界面黏附作用规律对于基于石墨烯的器件设计及其转移技术具有重要的意义.

目前,研究者们主要通过理论和实验方法探讨石墨烯膜与基底之间的黏附作用特性.Koenig等[12]通过实验测量了石墨烯在氧化硅上的黏附能,发现单层石墨烯的黏附力要比2—5层石墨烯在氧化硅上的黏附力高得多.随后,He等[13]通过理论方法分析也发现了氧化硅上单层石墨烯的界面分离能与黏附能要比多层石墨烯高,且随着温度的升高先增大后减小,这表明石墨烯与基底之间的界面性能可以通过薄膜厚度和温度刺激来进行调整.另外,仇巍等[14]通过拉曼实验技术测量了单层石墨烯与柔性基底的界面力学性能,研究发现界面切应力可将基底变形传递给石墨烯,而对于不同的基底变形,其传递变形的效率也不同.以上理论和实验研究主要是针对石墨烯层数、基底形变以及外界温度对石墨烯在基底表面上吸附过程的影响,而由于范德瓦耳斯力作用,石墨烯同样可以黏附在基底侧壁上,并且其效果主要取决于基底的相互作用、外界温度以及沟槽边缘的曲率[15].然而,Na等[16]通过测量CVD法制备的石墨烯在湿转移过程中与硅基底之间的附着力,发现石墨烯与硅分离的过程中产生的相互作用要比范德瓦耳斯作用大很多,这说明还存在其他作用力影响.2016年,Kumar等[17]结合有限元分析和分子动力学方法,发现石墨烯与硅基底之间除了存在宏观的范德瓦耳斯作用力,还存在一种微观点状的相互作用,这是由于石墨烯附着在SiO2表面的缺陷点位处.由此可见,基底织构是影响石墨烯吸附过程中的形变和作用力的重要因素.本文采用分子动力学方法研究铜基底织构对石墨烯的吸附作用特性,考虑凹槽织构几何特征尺寸对石墨烯吸附力的影响机制,揭示石墨烯在转移过程中与目标基底的相互作用特性和形变规律,为基于石墨烯的器件设计及其转移技术提供一定的理论指导.

2 模型与方法

2.1 系统模型

本文采用经典分子动力学软件LAMMPS模拟和分析石墨烯在铜基底上吸附及剥离的过程.由于在铜(111)结构上生长的石墨烯质量高于在铜(100)结构上的生长质量[18],因此,本文中的铜基底均采用(111)结构,如图1(a)所示.图中铜基底长为15.33 nm,宽为15.33 nm,石墨烯长为18.3 nm,宽为15.33 nm,其中,石墨烯两端固定区域在x方向的宽度为1.5 nm.图1(b)给出的是在铜基底表面构建具有不同深宽值的凹槽初始模型.图1(c)为吸附过程模型:给带有凹槽的铜基底施加一个恒定速度vsub使基底向z轴正向移动,匀速靠近石墨烯,达到平均距离后,停止运动.吸附过程完成后,给基底施加恒定速度−vsub使基底向z轴负方向匀速运动,即为石墨烯剥离过程,如图1(d)所示.

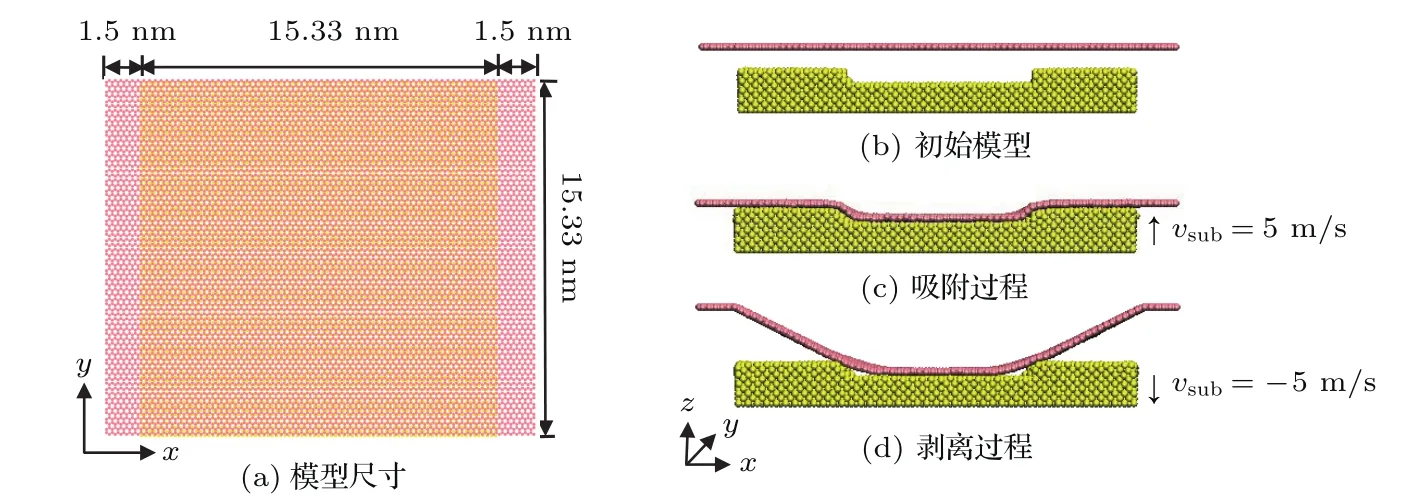
图1 石墨烯在铜基底上吸附作用模型(a)模型尺寸图;(b)石墨烯与基底吸附初始模型;(c)铜基底以5 m/s的速度匀速靠近石墨烯,即石墨烯吸附过程;(d)铜基底以5 m/s的速度远离石墨烯,即石墨烯剥离过程Fig.1.Model for the graphene sheet adsorbed by the copper substrate:(a)Graphene sheet model;(b)the initial model of graphene-copper substrate system;(c)the process of graphene adsorption with the moving speed of the copper substrate of 5 m/s;(d)the graphene stripping process with the speed of the copper substrate of 5 m/s.

2.2 模拟细节及参数设置

本文中分子动力学模拟的时间步长设为0.001 ps(1 ps=10−12s).分子动力学模拟系统中x,y,z均采用非周期性边界条件.采用二阶AIREBO势能函数[19]来描述石墨烯上碳原子之间的相互作用.采用精确的嵌入原子势[20,21]描述铜原子之间的相互作用,其形式如下:

式中,ρi是第i个原子所在位置处的电子密度,Fi(ρi)为镶嵌能函数,rij为原子i与原子j之间的距离;ϕij(rij)为两体中心势.本文采用Lennard-Jones(LJ)势[22]描述石墨烯碳原子和铜原子之间的相互作用,其表达式如下:

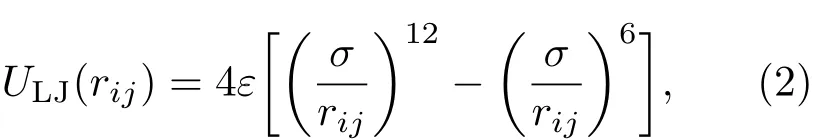
式中,ε为势阱深度,σ为平衡距离,rij为原子i与原子j之间的距离.对于碳-铜相互作用,是通过Lorentz-Berthelot方程混合法则求得出的,其中,εCuC=0.02578 eV,σCuC=3.0825 Å[23],该参数在Guo等[23]通过分子动力学模拟铜纳米线在缺陷碳管中的结构演变研究中得到了很好的验证,LJ的截断半径设为8 Å.为了让模拟更加接近自然状态,在石墨烯与铜基底相互作用之前,系统将会弛豫100 ps.文中所获得的分子动力学数据均为10 ps时间内进行统计平均的结果.

3 结果分析与讨论

为了探究铜基底表面凹槽的几何特征尺寸对石墨烯吸附作用的影响规律,首先模拟研究了凹槽深度对石墨烯吸附特性的影响.初始情况下,保持凹槽宽度为4 nm不变,而凹槽深度变化分别为0(无凹槽),0.256,0.362,0.572,0.722,0.922 nm,相当于每次去除一层铜原子,此处用d表示基底凹槽的深度.模拟石墨烯吸附基底的过程是通过给铜基底施加5 m/s的速度使之匀速靠近石墨烯,待达到石墨烯与基底之间的平均距离之后,铜基底停止运动,从而获取该模拟周期内铜基底对石墨烯的吸附作用力随距离的变化.下文中用D表示石墨烯固定端与铜基底上表面之间的垂直距离,用H表示铜基底表面凹槽的宽度,用d表示铜基底表面凹槽的深度.图2(a)给出的是石墨烯吸附过程中不同凹槽深度情况下的吸附作用力随距离D的变化.为了深入发掘基底对石墨烯的吸附特性,同时给出了石墨烯在吸附过程中的微观构型,如图3(a)—(c)所示.从图2(a)可以看出,当D=0.82 nm时,开始出现微弱的吸附力,此时石墨烯表面波动较明显(图3(a));随后,继续缩小铜基底与石墨烯之间的距离,石墨烯与基底之间的吸附力几乎呈线性趋势迅速增大(在吸附力出现突变处,加密了位移在0.70—0.82 nm的数据点,如图2(b)所示),直到当D=0.72 nm时,由于凹槽上方的石墨烯吸附到凹槽内(图3(c)),而靠近石墨烯两固定端处的石墨烯产生局部拉应力,导致此时石墨烯与基底之间的作用力达到最大值;最后,随着石墨烯与基底之间距离继续减小,吸附结构逐渐趋于稳态(图3(c)),相应的吸附力也逐渐减小并趋于稳定.从图2(a)还可以发现,吸附作用力最大的位置在距离D约为0.72 nm处,从而获得在D=0.72 nm处的最大吸附作用力随凹槽深度的变化,如图4(a)所示.随着凹槽深度的逐层加深,吸附力也随之增大;当凹槽深度d增加到0.572 nm(即3层铜原子厚度)时,吸附力最大,约为133×10−9N.当继续增加凹槽深度时,吸附作用力将迅速减小,此时石墨烯距离凹槽底部的距离已经超出截止半径的大小,所以石墨烯不能完全嵌入并铺展在凹槽的底部(图5(a)—(e)).我们同时考虑了凹槽宽度变化对石墨烯吸附作用的尺寸效应,将凹槽宽度固定为8 nm不变,同样改变凹槽深度,获取在D=0.72 nm处的最大吸附作用力随凹槽深度的变化曲线,如图4(b)所示,结果发现,基底对石墨烯的最大吸附作用力仍然发生在凹槽深度d=0.572 nm的情况,且与凹槽宽度为4 nm时具有相似的变化趋势.

图2(a)固定边界条件下,凹槽宽度为4 nm时,具有不同凹槽深度的基底对石墨烯的吸附作用力随其间距D的变化,D范围变化为0.9–0.316 nm;(b)为D区间在0.70–0.82 nm时的局部放大图Fig.2.(a)The adsorption force between graphene and Cu substrate as a function of D for different depths of the groove with the width of 4 nm and D changing in the range of 0.9–0.316 nm,and the two boundaries of the graphene sheet in x direction are fixed boundary condition;(b)the local view with D in the range of 0.70–0.82 nm.

图3 石墨烯与基底吸附作用过程中,其间距D在(a)0.82,(b)0.72和(c)0.35 nm时系统的微观构型Fig.3.The con figurations of the system for the graphene-substrate distance D of(a)0.82,(b)0.72 and(c)0.35 nm in the absorption process.

图4(a)D=0.72 nm,槽宽H为4 nm时,最大吸附作用力随深度d的变化;(b)D=0.72 nm,槽宽H为8 nm时,最大吸附作用力随深度d的变化Fig.4.(a)The maximum adsorption force as a function of the depth of groove d for D=0.72 nm and the groove width H=4 nm;(b)the adsorption force as a function of the depth of groove d for D=0.72 nm and H=8 nm.

机械剥离法是石墨烯基底转移技术中的重要方法,因此我们模拟研究了石墨烯从带有凹槽的铜基底上剥离过程中的吸附作用特性.通过给铜基底施加恒定的速度为5 m/s,且保持石墨烯两端固定,使铜基底匀速脱离石墨烯,由于石墨烯两端固定,石墨烯从两端向中间逐渐从基底上剥离.图6给出的是不同凹槽深度情况下,石墨烯剥离过程中的吸附作用力随距离D的变化.可以看出,起初随着距离的增大,石墨烯与基底之间吸附力逐渐增大,而当距离D增加到某一临界值Fc时,石墨烯与基底之间的吸附力迅速减小至消失,说明此刻石墨烯已从基底上完成了剥离过程.重要的是,石墨烯完全剥离的临界作用力Fc随凹槽深度的变化呈现先增大后减小的趋势,且没有凹槽时的剥离临界作用力Fc大于凹槽深度大于0.572 nm时的情况,且在凹槽深度为0.362时临界剥离作用力最大(见表1).说明石墨烯与凹槽基底的吸附作用力取决于石墨烯与基底的相互作用能,而对于近似各向同性的石墨烯与单晶铜界面,其相互作用能随界面接触面积增加而增大.凹槽深度的增加,增大了石墨烯与基底的接触面积,因此临界剥离作用力逐渐增加;而当深度大于0.572 nm时,由于石墨烯不能完全吸附在基底的凹槽内,导致界面接触面积甚至低于无凹槽的情况,因此临界剥离作用力也相应低于无凹槽的情况.

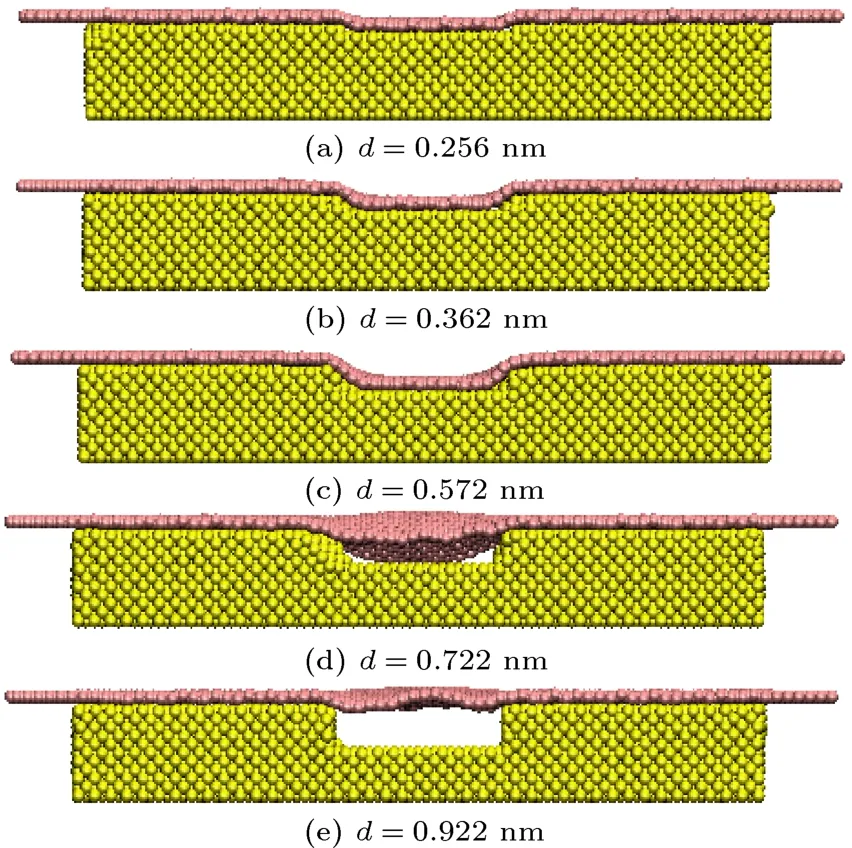
图5 D=0.35 nm,凹槽宽度为4 nm时,不同的凹槽深度(0.256–0.922 nm)下石墨烯与铜基底吸附之后的稳态构型Fig.5.In the case of groove width of 4 nm,the steady con figurations of the absorbed graphene at the distance D of 0.35 nm for the groove depth changing in the range of 0.256–0.922 nm.

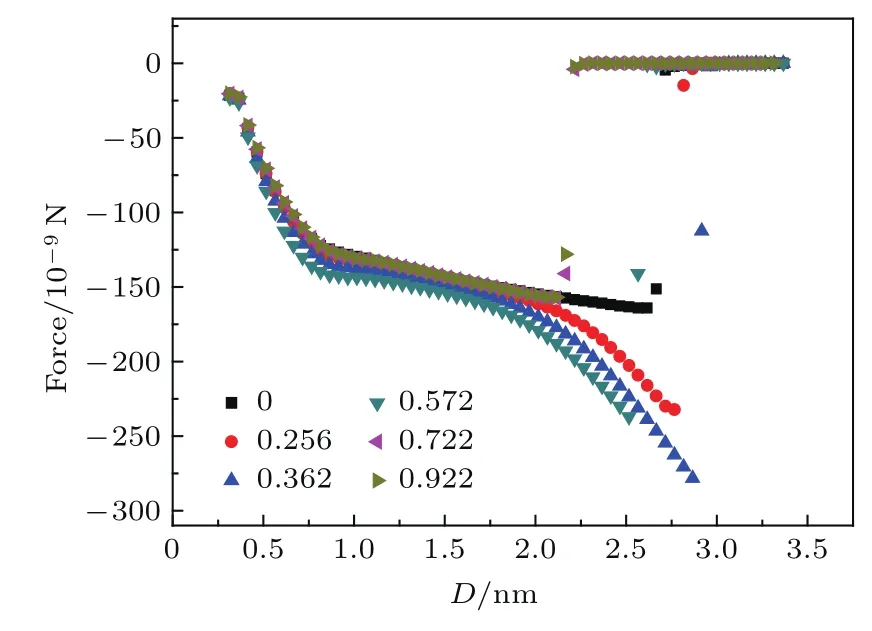
图6 石墨烯剥离基底过程,不同凹槽深度下石墨烯与铜基底之间吸附力随距离D的变化,D范围变化为0.316–2.916 nm,凹槽深度变化范围为0–0.922 nm,0表示没有凹槽的情况Fig.6.In the graphene stripping process,the adsorption force between graphene and substrate as a function of D for different depths of grooves which are changed ranging from 0–0.922 nm;zero is representative of no-groove-substrate system.

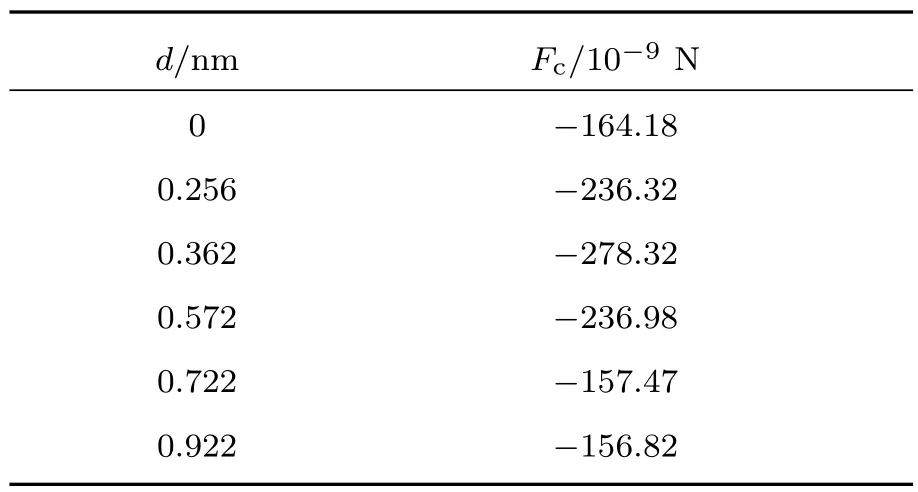
表1 不同凹槽深度d的临界剥离作用力Fc参数表Table 1.The parameter table of critical adsorption force Fcwith different depths of grooves.

由上述结果可知,对于宽度为4 nm的凹槽基底,当凹槽深度为0.572 nm(即三层铜原子厚度)时,石墨烯与铜基底之间的吸附作用最强.紧接着,保持凹槽深度为0.572 nm不变,研究凹槽宽度H的变化对吸附作用力的影响规律.图7(a)给出了凹槽宽度在0—5.607 nm之间变化时,凹槽基底对石墨烯的吸附作用力随距离D的变化,由于在距离D为0.70—0.82 nm范围内的吸附力出现突变,我们同样加密了该范围内的数据点,如图7(b)所示.结果表明,吸附作用力随其二者间距的变化曲线大致可以分成两组:第一组是凹槽宽度低于2.717 nm时,该结构的基底与石墨烯之间的吸附作用变化趋势一致,且作用力相对较小,其吸附力的最大值约为120×10−9N;第二组是基底表面的凹槽宽度大于2.717 nm时,凹槽基底与石墨烯之间的吸附作用曲线几乎重叠,且吸附力明显高于第一组的情况,其吸附作用力的最大值约为137×10−9N.为了深入挖掘这两组情况的吸附作用变化机理,图8给出了不同凹槽宽度情况下石墨烯与凹槽基底系统的吸附稳态构型.显然,当铜基底表面凹槽宽度为1.996和2.717 nm时,由于凹槽宽度较窄,石墨烯并未被吸附到基底凹槽内;而当铜基底表面的凹槽宽度大于2.717 nm时,石墨烯均完全被吸附在基底的凹槽内.对于石墨烯未被吸附进入凹槽内的情况(H≤2.717 nm),由于凹槽宽度的变化引起石墨烯与凹槽基底接触面积的略微变化,进而导致凹槽宽度H为1.996和2.717 nm时吸附作用力变化曲线没有完全重合;而对于石墨烯完全吸附凹槽内部的情况(H＞2.717 nm),凹槽宽度的变化没有改变石墨烯与凹槽基底的接触面积,因此该组四条吸附作用力变化曲线完全重合.

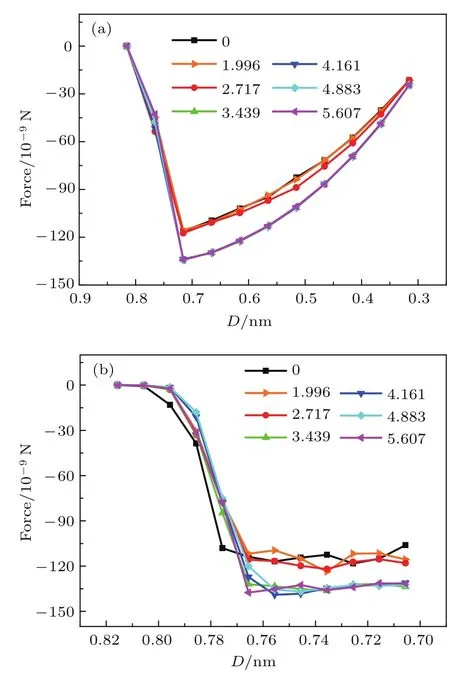
图7(a)石墨烯吸附过程中,不同凹槽宽度下石墨烯与凹槽基底之间的吸附作用力随其间距D的变化,D变化范围为0.9–0.316 nm;(b)为D区间在0.70–0.82 nm 时的局部放大图Fig.7.(a)The adsorption force between graphene and grooved substrate as a function of D for different width of grooves in the graphene adsorbing process,and D is changed ranging from 0.9 nm to 0.316 nm;(b)the local view with D in the range of 0.70–0.82 nm.

图8 当铜基底表面凹槽深度为0.572 nm,宽度分别为(a)1.996,(b)2.717和(c)3.439 nm时的石墨烯吸附的稳态构型Fig.8.Con figurations of graphene adsorbing on the copper substrate for the groove width of(a)1.996,(b)2.717 and(c)3.439 nm respectively,while keeping the groove depth of 0.572 nm as a constant.

同样地,保持凹槽深度为0.572 nm不变,考虑了铜基底凹槽宽度H在石墨烯剥离过程中的影响,并对其在剥离过程中的吸附作用力及微观构型进行了研究.从图9可以看出,当铜基底表面凹槽宽度为1.996和2.717 nm时,由于石墨烯没有被吸附在基底的凹槽内,石墨烯在剥离铜基底的过程中产生的吸附作用几乎一致,当吸附力达到160×10−9N时,石墨烯完成剥离过程,吸附作用迅速减小并最终消失;而当铜基底表面凹槽宽度H大于2.717 nm时,由于此时的石墨烯与基底在吸附过程中可以完全被吸附于基底凹槽内,石墨烯在剥离铜基底过程中所受的吸附作用力明显强于H≤2.717 nm的情况.此外,还可以发现,当二者间距D小于1.75 nm时,基底表面凹槽宽度变化对吸附作用的影响不明显,而当间距D大于1.75 nm时,随着基底凹槽宽度的变宽,石墨烯在剥离过程中所受到的吸附作用力呈现增强的趋势.

从上述研究我们发现,对于在x方向上固定边界条件的石墨烯,当基底凹槽的深度为0.572 nm不变,石墨烯与基底之间的吸附作用力主要取决石墨烯与基底凹槽之间相互作用的微观构型,且宽度在2.717 nm附近变动时,出现了由未吸附进入到完全吸附进入凹槽的转变.由此,我们进一步探索了基底凹槽深度固定、宽度在2.0—3.1 nm范围内变化时石墨烯在基底凹槽内的吸附稳态构型,如图10所示.当基底凹槽宽度为2.0 nm时,石墨烯完全不能吸附于基底凹槽内,而当基底凹槽宽度为2.5,2.7和2.9 nm时,石墨烯只能局部吸附于基底的凹槽内,直到基底凹槽宽度增大至3.1 nm时,石墨烯可以完全吸附于凹槽内,并且从吸附构型图中能够发现随着基底凹槽宽度缓慢增大,能够吸附进入基底凹槽内的面积越大.此外,石墨烯在凹槽内发生局部吸附的过程中,其自身经历了从凹槽两端逐步向中间吸附,直至完全吸附于凹槽内的过程.

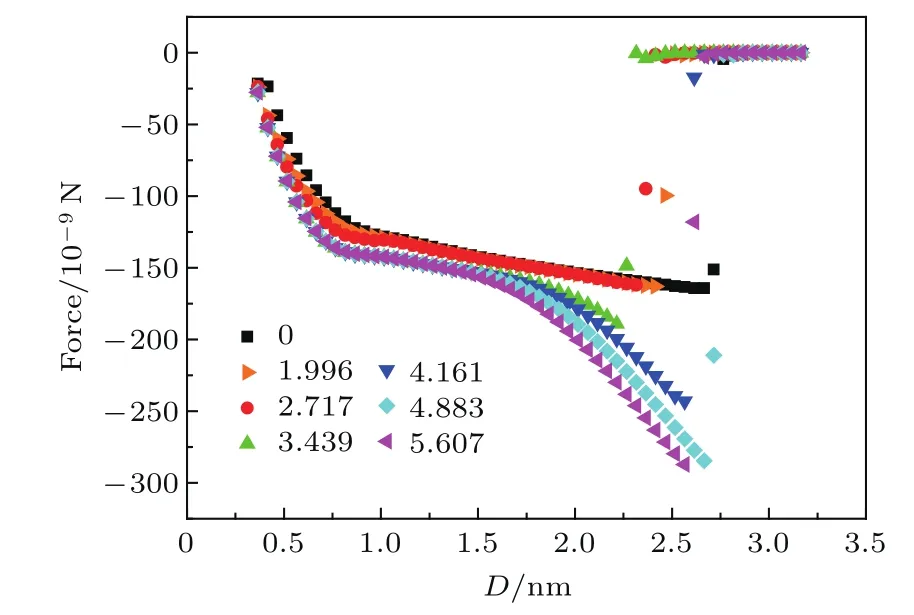
图9 石墨烯剥离过程中,不同凹槽的宽度下石墨烯与铜基底之间吸附力随间距D的变化,D范围变化为0.316–2.56 nmFig.9.The adsorption force between graphene and substrateasa function ofD fordifferent width of grooves in the graphene stripping process.D is changed ranging from 0.316 nm to 2.56 nm.

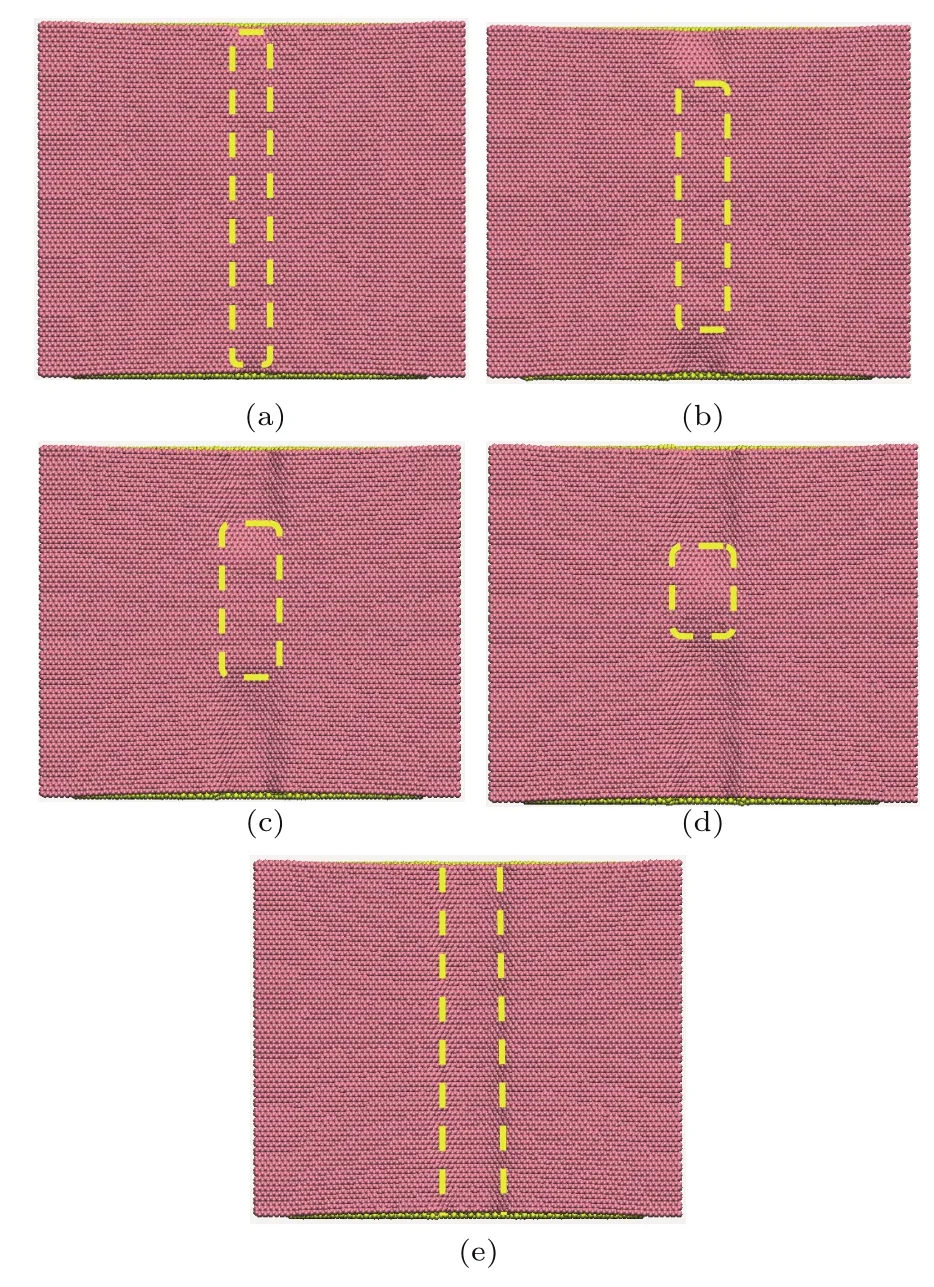
图10 石墨烯吸附基底过程,凹槽深度为0.572,H在(a)2.0,(b)2.5,(c)2.7,(d)2.9,(e)3.1 nm时的吸附构型Fig.10.Con figurations of graphene adsorbing on the copper substrate where the depth of grooves is 0.572 nm and H is changed at(a)2.0,(b)2.5,(c)2.7,(d)2.9,(e)3.1 nm.

以上研究结果都是基于石墨烯在x方向上两侧施加固定边界条件下获取的,而石墨烯在与基底表面凹槽相互作用时,该固定边界条件必然会导致石墨烯面内产生残余应力,从而引发石墨烯与基底凹槽的吸附作用微观构型的变化.于是,我们研究了石墨烯在自由边界条件下石墨烯与带有凹槽的基底表面的吸附作用特性.为了直观地观察到石墨烯边界处的影响,重新构建了石墨烯模型,如图11(a)所示,其在x-y平面内的大小为15.26 nm× 15.33 nm,石墨烯整体处于自然弛豫状态,边界均不固定.结果表明,即使铜基底表面凹槽的宽度小至1.084 nm,石墨烯仍可以完全被吸附于基底凹槽内,图11(b)所示,而随着铜基底表面凹槽的宽度继续减小至0.723 nm,此时凹槽宽度非常狭窄,凹槽吸附作用不能克服石墨烯在狭窄凹槽处变形的弯曲能,从而未能吸附至凹槽内,如图11(c)所示.并且,与两端固定边界条件下的石墨烯吸附现象不同的是,石墨烯在凹槽处的吸附变形导致石墨烯边界在吸附之后均向凹槽中心位置缩进,(图11(d)和图11(e)),从而降低了固定边界吸附过程中需要克服预紧力的影响.由于石墨烯的边界效应将对石墨烯与其他材料的界面相互作用特别是摩擦特性具有重要的影响,因此,自由边界条件下石墨烯与凹槽基底的相互作用特性随凹槽几何参数的变化规律有待于在将来的工作中进一步讨论.

图11 石墨烯两端不固定,铜基底凹槽深度为0.572 nm、宽度为2 nm时,基底与石墨烯之间的吸附现象(a)模型尺寸;宽度分别为(b)1.084,(c)0.723 nm时的石墨烯吸附的稳态构型;石墨烯吸附基底的(e)前、(d)后对比图,虚线为石墨烯吸附前后的其边界位置的变化Fig.11.The process of graphene adsorbing on the substrate with the depth of groove is 0.767 nm for the graphene is un fixed:(a)The dimensions of the model;con figurations of graphene absorbing on the copper substrate for H of(b)1.804,(c)0.723 nm;image contrast of un fixed graphene adsorbing on the substrate(d)before and(e)after.The dashed lines represent the changes of the location of the graphene edges.

4 结 论

本文采用分子动力学方法对凹槽铜基底表面上的单层石墨烯吸附特性进行了研究,通过改变铜基底表面凹槽的几何特征尺寸,系统地模拟并研究了石墨烯在凹槽基底上吸附和剥离的两个过程中其吸附作用力随二者间距和凹槽深度、宽度的变化规律.在石墨烯吸附过程中,对于固定边界条件下的单层石墨烯,基底表面的凹槽宽度固定不变时,凹槽基底对石墨烯的吸附力随二者间距的减小,呈现先增大后减小的趋势;其最大吸附力随凹槽深度的增加而增大,而当凹槽深度继续增大至石墨烯未能吸附进入凹槽底部的临界值时,最大吸附力迅速减小.在石墨烯剥离过程中,石墨烯与凹槽基底的相互作用力随着二者间距的增加逐渐增大,当达到某一临界值后突然急剧减小至消失.从模拟结果得出,该临界值即为石墨烯完全从基底上剥离的临界作用力.石墨烯完全剥离的临界作用力随凹槽深度的增加,同样呈现先增大后减小的趋势,且与剥离前石墨烯的吸附稳态构型有关.当基底表面凹槽的深度固定不变时,吸附和剥离过程中石墨烯-基底之间的吸附力随间距的变化规律取决于石墨烯能否被凹槽完全吸附在凹槽内部,变化趋势依据石墨烯“完全吸附在凹槽内部”和“覆盖在凹槽之上”两种情况清晰地分成了两组,且每一组中的石墨烯与基底之间的吸附作用力都与二者的相互作用面积有关.此外,我们还发现石墨烯的固定边界条件所产生的其自身面内拉应力明显限制了石墨烯吸附进入凹槽内部的行为,并初步探讨了自由边界条件下石墨烯能够吸附进入表面凹槽的临界宽度.研究结果不仅可为石墨烯与织构基底的转移和剥离技术提供理论基础,并将可能为基于石墨烯的纳米器件制作和表面修饰提供帮助.

[1]Novoselov K S,Geim A K,Morozov S V,Jiang D,Zhang Y,Dubonos S V,Grigorieva I V 2004 Science 306 666

[2]Geim A K 2009 Science 324 1530

[3]Castro Neto A H,Guinea F,Peres N M R,Novoselov K S,Geim A K 2009 Rev.Mod.Phys.81 109

[4]Lee C,Wei X,Kysar J W,Hone J 2008 Science 321 385

[5]Damm C,Nacken T J,Peukert W 2015 Carbon 81 284

[6]Oliveira Jr M H,Schumann T,Gargallo-Caballero R,Fromm F,Seyller T,Ramsteiner M,Trampert A,Geelhaar L,Lopes J M J,Riechert H 2013 Carbon 56 339

[7]Stankovich S,Dikin D A,Piner R D,Kohlhaas K A,Kleinhammes A,Jia Y,Wu Y,Nguyen S T,RuoffR S 2007 Carbon 45 1558

[8]Li H,Fu Z B,Wang H B,Yi Y,Huang W,Zhang J C 2017 Acta Phys.Sin.66 058101(in Chinese)[李浩,付志兵,王红斌,易勇,黄维,张继成2017物理学报66 058101]

[9]Tyurnina A V,Okuno H,Pochet P,Dijon J 2016 Carbon 102 499

[10]Kang J,Shin D,Bae S,Hong B H 2012 Nanoscale 4 5527

[11]Bunch J S,Zande A M V D,Verbridge S S,Frank L W,Tanenbaum D M,Parpia J M,Craighead H G,McEuen P L 2007 Science 315 490

[12]Koenig S P,Boddeti N G,Dunn M L,Bunch J S 2011 Nat.Nanotechnol.6 543

[13]He Y,Yu W,Ouyang G 2015 J.Phys.Chem.C 119 5420

[14]Qiu W,Zhang Q P,Li Q,Xu C C,Guo J G 2017 Acta Phys.Sin.66 166801(in Chinese)[仇巍,张启鹏,李秋,许超宸,郭建刚2017物理学报66 166801]

[15]Budrikis Z,Zapperi S 2016 Nano Lett.16 387

[16]Na S R,Ji W S,RuoffR S,Rui H,Liechti K M 2014 ACS Nano 8 11234

[17]Kumar S,Parks D,Kamrin K 2016 ACS Nano 10 6552

[18]Wood J D,Schmucker S W,Lyons A S,Pop E,Lyding J W 2011 Nano Lett.11 4547

[19]Brenner D W,Shenderova O A,Harrison J A,Stuart S J,Sinnott S B 2002 J.Phys.:Condens.Mater.14 783

[20]Hu C,Bai M,Lü J,Wang P,Zhang L,Li X 2014 Micro fluid.Nano fluid.17 581

[21]Foils S M,Baskes M I,Daw M S 1986 Phys.Rev.B 33 7983

[22]Jones J E 1924 Proc.Roy.Soc.London Ser.A 106 441

[23]Guo Y,Guo W 2006 Nanotechnology 17 4726