BH+离子基态及激发态的势能曲线和跃迁性质的研究∗

罗华锋 万明杰 黄多辉

1)(宜宾学院化学与工程学院,宜宾 644007)

2)(宜宾学院,计算物理四川省高等学校重点实验室,宜宾 644007)

1 引 言

BH+离子和其同位素离子BD+的第一激发态A2Π到基态X2Σ+的跃迁都具有较短的自发辐射寿命τ和高对角分布的弗兰克-康登因子f00,其中BH+和BD+离子A2Π态的辐射寿命分别约为238 ns[1]和235 ns[2],弗兰克-康登因子分别为:f00(BH+)=0.947[3],f00(BD+)=0.923[2].两种离子在理论上都被预测为激光冷却的候选离子[1,2].

实验上对BH+离子的光谱性质进行了较为广泛的研究[4−8].1937年,Almy和Horsfall[4]首次从实验上得到了BH+离子基态X2Σ+的光谱常数,并给出了A2Π→X2Σ+跃迁0-0带的跃迁能ν00=26376.2 cm−1.1964年,Bauer等[5]指出BH+离子基态的离解能比BH分子基态的离解能小1.47 eV.1981年,Ottinger和Reichmuth[6]通过化学发光反应B++H2→BH+(A2Π)+H观测到了BH+的A2Π→X2Σ+跃迁.并给出了A2Π态的光谱常数.Ramsay和Sarr[7]通过高分辨率拍摄BH+的A2Π→X2Σ+跃迁得到了X2Σ+和A2Π态的光谱常数.2006年,Viteri等[8]报道了11BH+基态X2Σ+的最新实验成果,并得到了更加精确的光谱常数.

理论上主要集中在BH+离子的基态和第一激发态的势能曲线研究[1,3,9−11].1977年,Rosmus和Meyer[9]分别采用赝势轨道组态相互作用(PCOCI)和耦合电子对方法(CEPA)计算了BH+离子基态的势能曲线,并得到了其光谱常数.1981年,Guest和Hirst[10]采用多参考双重激发组态相互作用方法(MRDCI)计算了其前三个离解极限的势能函数,给出了X2Σ+,A2Π和B2Σ+态的光谱常数.1982年,Klein等[11]计算了BH+离子最低3个电子态的光谱常数,并给出了BH+离子的偶极矩和跃迁偶极矩.1984年,Kusunoki[3]计算了BH+离子X2Σ+,A2Π,B2Σ+,a4Π和b4Σ−态的光谱常数.文中指出24Π为排斥态,b4Σ−态为第一四重激发态.同时给出了A2Π→X2Σ+,B2Σ+→X2Σ+和b4Σ−→a4Π跃迁的弗兰克-康登因子.2011年,Nguyen等[1]选用aug-cc-pV5Z全电子基组,在采用多参考组态相互作用单双激发方法(MRCISD)和完全相互作用方法(FCI)精确地计算了BH+离子最低3个电子态的光谱常数,并给出了A2Π态的辐射寿命.

本文采用MRCI方法系统的研究了BH+离子最低4个离解极限的9个Λ—S态的势能曲线及其跃迁性质.计算得到:除了22Π态为排斥态外,其他电子态均为束缚态,并且32Π和42Σ+态具有双势阱结构.利用LEVEL8.0程序拟合了弗兰克-康登因子和自发辐射寿命等性质.B2Σ+与A2Π态的势能曲线在弗兰克-康登区域出现相交情况,本文在考虑自旋-轨道耦合效应 (SOC)下讨论了两个电子态的相交对激光冷却BH+离子的影响.

2 计算方法

BH+离子9个Λ—S态的电子结构都由MOLPRO 2010程序[12]计算得到,由于程序限制,本文计算采用C2V子群.首先采用Hartree-Fock方法[13]产生BH+离子的初始猜测分子轨道;然后采用完全活性空间自洽场方法(CASSCF)[14,15]对初始轨道进行优化,得到态平均的多组态波函数;最后采用MRCI[16,17]及Davidson修正(+Q)得到最终的波函数.在MRCI+Q计算的基础上考虑了SOC,SOC效应通过Breit-Pauli算符来实现[18].

C2v群有4个不可约表示(a1,b1,b2,a2).在CASSCF计算中,B(1s)为双占据的闭壳层轨道,H(1s2s2p3s3p)和B(2s2p)轨道为活性轨道,可以写为CAS(5,13);在随后MRCI+Q计算中考虑了核-价电子(CV)关联效应,即B(1s)轨道参与电子关联的计算.对于B原子,本文选用了考虑CV关联的aug-cc-pCV5Z-DK(ACV5Z-DK)全电子基组[19],H原子选用aug-cc-pV5Z-DK(AV5Z-DK)全电子基组[20].为方便起见,文中H AV5Z-DK基组写为ACV5Z-DK.

本文采用Murrell-Sorbie(M-S)[21]来拟合各个电子态的光谱常数.为描述拟合的效果,文中给出了均方根值(RMS).此外弗兰克-康登因子、辐射速率和辐射寿命均采用LEVEL8.0程序[22]来拟合.

3 结果与讨论

本文在MRCI+Q/ACV5Z-DK水平下计算了BH+离子的前4个离解通道所对应的9个Λ—S态的势能曲线.原子态和分子态的对应关系列于表1中.其中基态X2Σ+对应于最低离解通道B+(1Sg)+H(2Sg),A2Π,B2Σ+,a4Π和b4Σ+态有共同离解通道B+(3Pu)+H(2Sg).前两个离解通道之间的能量差为37523.6 cm−1,比Moore的实验值[23]大178.6 cm−1,误差仅为0.48%.第三离解通道源自H原子的电离,即B(2Pu)+H+(1Sg),此离解通道对应于22Π,32Σ+态,并与第一离解通道的能量差为43106.5 cm−1,与实验值[23]的误差为0.83%.第四离解通道B+(1Pu)+H(2Sg)与第一离解通道的能量差为74032.9 cm−1,与实验值[23]的误差为0.87%.可以看出本文计算结果与实验值符合较好.

表1 BH+离子分子态与原子态的离解关系Table 1.Dissociation relationships between molecular states and atomic states of BH+.

3.1 势能曲线与光谱常数

计算的9个Λ—S态的势能曲线见图1.除22Π电子态外,其他电子态均为束缚态.利用M-S函数对束缚态进行拟合所得到的光谱常数与已有实验值及其他理论计算值列于表2中.

本文所计算基态X2Σ+在平衡位置处其主要电子组态为1σ22σ23σα,权重为94.48%. 其平衡核间距Re为1.20485 Å,谐振频率ωe和非谐振频率ωeχe分别为2518.36 cm−1和64.62 cm−1,与最新报道的实验值[8]分别相差0.00156 Å,8.44 cm−1和2.64 cm−1.误差只有0.13%,0.33%和4.26%.Bauer等[5]从实验上得到BH+离子基态的离解能比BH分子基态的离解能小1.47 eV.学者们分别从实验和理论两方面研究了BH分子基态的离解能[24,25]Huber和Herzberg[24]总结前人实验得到BH分子基态的离解能D0=3.42 eV,可以得到BH+离子基态的离解能D0=1.95 eV,本文的计算值仅比实验值高0.032 eV,误差为1.64%.

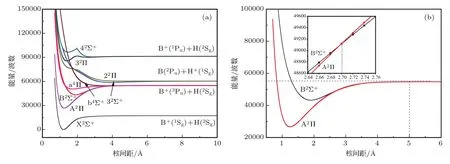
图1 (a)BH+离子Λ—S态的势能曲线;(b)A2Π和B2Σ+态的势能曲线Fig.1.(a)Potential energy curves for the Λ–S states of BH+;(b)potential energy curves for the A2Π and B2Σ+states of BH+.

表2 BH+离子Λ—S态的光谱常数Table 2.Spectroscopic constants for the Λ–S states of BH+.

第一激发态A2Π在平衡位置处的主要电子组态为1σ22σ21πα, 权重为86.23%. 次要电子组态为1σ22σα3σβ1πα和1σ22σα3σα1πβ, 权重分别为7.06%和2.12%. X2Σ+→A2Π跃迁主要是由3σα →1πα的跃迁. 其绝热激发能Te为26689.72 cm−1.通过LEVEL8.0程序计算得到其考虑零点能后0-0带的跃迁能ν00=26533.14 cm−1. 实验上,Almy[4],Ottinger[6],Ramsay小组[7]分别得到ν00的值为26376.2,26368.18和26375.90 cm−1. 本文结果与实验值的误差约为0.60%.A2Π态具有很深的势阱,其势阱深度De为3.4842 eV.通过表2可以看出A2Π态的其他光谱常数均与实验值[6,7]符合得较好.例如:δRe/Re=0.29%,δωe/ωe=1.80%.

第二激发态B2Σ+在平衡位置处的主要电子组态由两部分组成, 即1σ22σα3σ2(49.29%)和1σ22σ24σα(37.88%),而1σ22σ23σα的权重降为2.46%,基本可以忽略.也就是说X2Σ+→B2Σ+的跃迁主要是由2σβ →3σα和3σα →4σα跃迁的叠加而成.其位于比基态高43241.12 cm−1处,而且其具有较深的势阱,De=1.432 eV.B2Σ+与A2Π态的势能曲线约在2.7 Å出现相交情况,此区域在A2Π→X2Σ+跃迁的弗兰克-康登区域以内.这两个态势能曲线的相交对激光冷却的影响将在第3.3节来详细讨论.到目前为止,还没有关于B2Σ+态的光谱常数的实验报道.本文只和采用FCI方法的计算值[1]进行对比.本文计算的X2Σ+,A2Π和B2Σ+态的光谱常数与FCI/AV5Z水平下的计算值[1]的最大误差不超过1%.

a4Π为四重态的基态,在平衡位置处其主要电子 组 态为1σ22σα3σα1πα, 权 重 为97.29%.X2Σ+→a4Π跃迁主要是由2σα →1πα的跃迁引起的.其绝热激发能为50539.17 cm−1.到目前为止,只有Kusunoki[3]计算了四重态的光谱数据,由于基组和方法的选择问题,a4Π态的计算结果精确度不高.Kusunoki的计算结果表明b4Σ+为排斥态[3],确定4Σ−为四重态的第一激发态,本文采用高精度的量化计算得到了b4Σ+态是一个势阱很小的束缚态,其势阱深度De只有0.0158 eV,我们重新确定b4Σ+为四重态的第一激发态.b4Σ+态的势阱太小可能是导致Kusunoki得到其为排斥态的原因.32Π和42Σ+电子态都具有双势阱结构.两个电子态分别在2.0 Å和1.96 Å左右发生预解离.原因是32Π和42Σ+电子态和更高的2Π和2Σ+态在此位置发生了避免交叉的现象.32Π和42Σ+态第一势阱的平衡位置(势阱深度)分别为1.39819 Å(0.7635 eV) 和1.46892 Å(0.5522 eV);第二势阱的平衡位置(势阱深度)分别为2.57597 Å(0.1600 eV)和2.89825 Å(0.0917 eV).其他的光谱常数也列在表2中. 其中b4Σ+,32Σ+,32Π和42Σ+态的光谱常数为首次报道.

为了评估势能曲线的拟合质量,本文同时给出了RMS值,列在表2中.可以看出所有的RMS值都很小.最大误差仅为3.407 cm−1,其余的误差不超过0.7 cm−1.可以看出本文的计算结果是可靠的.

3.2 跃迁性质

本文计算了BH+分子的A2Π→X2Σ+,B2Σ+→X2Σ+,32Σ+→X2Σ+,B2Σ+→A2Π,32Π→X2Σ+和b4Σ+→a4Π的跃迁偶极矩.跃迁偶极矩随核间距变化的曲线见图2.由于22Π为排斥态,故没有给出22Π→X2Σ+的跃迁偶极矩.

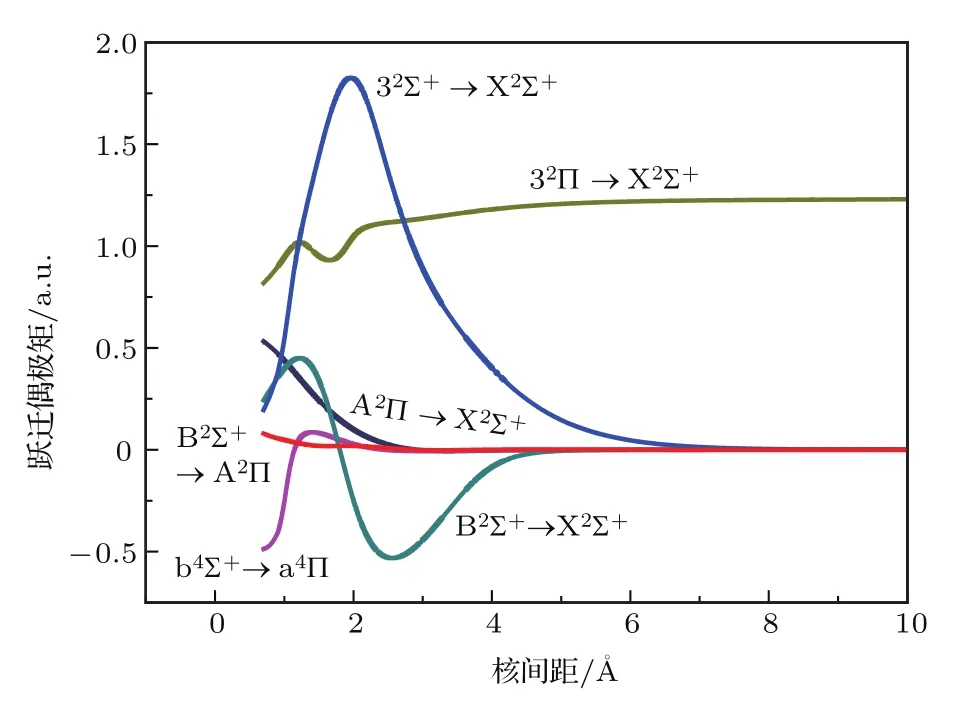
图2 BH+离子的跃迁偶极矩Fig.2.Transition dipole moments of BH+.

从图2中可以看出在核间距为10 Å时,A2Π→X2Σ+,B2Σ+→X2Σ+,32Σ+→X2Σ+,B2Σ+→A2Π和b4Σ+→a4Π的跃迁偶极矩趋于0,原因是X2Σ+,A2Π,B2Σ+,32Σ+,b4Σ+和a4Π态全部来源于B+离子的2s→2p轨道的跃迁,H原子处于基态;而32Π→X2Σ+的跃迁偶极矩趋近于另一极限(1.2323 a.u.),原因是32Π态来源于不同的原子激发,B原子处于基态,H原子被电离为H+离子.Nguyen等[1]在MRCI/AV5Z水平计算了A2Π→X2Σ+,B2Σ+→X2Σ+和B2Σ+→A2Π的跃迁偶极矩,在核间距为1.25 Å时分别为0.3383,0.4493和0.0295 a.u.本文对应的计算结果分别为0.3389,0.4489和0.0294 a.u.,本文结果和Nguyen等的结果误差不超过0.5%.同时可以看出A2Π→B2Σ+的跃迁强度很低.

本文也预测了A2Π→X2Σ+,B2Σ+→X2Σ+和B2Σ+→A2Π跃迁的爱因斯坦系数Aν′ν′′,弗兰克-康登因子fν′ν′′以及A2Π 和B2Σ+态的辐射寿命τ,其中ν′和ν′′分别表示终态和初态的振动量子数.对于A2Π→X2Σ+跃迁,本文计算的A00和A01分别为4.122×106s−1和5.852×104s−1,Nguyen等[1]计算得到τ00和τ01分别为241 ns和17µs,即A00=4.149×106s−1,A01=5.88×104s−1;本文计算的f00为0.9414,而Kusunoki[3]的计算值为0.947.对于B2Σ+→X2Σ+跃迁,由于两个电子态的平衡核间距相差太大,弗兰克-康登因子不存在高对角分布.对应的辐射速率峰值不在对角元上,其辐射速率的较大峰值在ν′′=6和ν′′=7,即A06=8.383×105s−1,A07=1.142×106s−1.同样对于B2Σ+→A2Π跃迁,其辐射速率的较大峰值在ν′′=3—5,由于其跃迁偶极矩在平衡位置附近很小,其辐射速率的值也很小,当ν′′=3—5时,A03=44.8 s−1,A04=62.7 s−1和A05=49.1 s−1.本文只列出了A2Π→X2Σ+跃迁的弗兰克-康登因子和爱因斯坦辐射系数,见表3.可以看出我们的计算值和Kusunoki的计算值[3]符合得很好.

表3 BH+离子A2Π→X2Σ+跃迁的爱因斯坦自发辐射系数(s−1)和弗兰克-康登因子Table 3.Einstein spontaneous emission coefficients Aυ′υ′′ (in s−1)and Franck-Condon factors fυ′υ′′ for A2Π → X2Σ+transition of BH+.

表4 BH+离子A2Π和B2Σ+态总辐射速率Atotal(s−1)和自发辐射时间 τ(ns)Table 4.Total emission coefficients Atotal(s−1)and radiative lifetime τ (ns)for the A2Π and B2Σ+states of BH+.

A2Π→X2Σ+,B2Σ+→X2Σ+和B2Σ+→A2Π跃迁 (ν′=0—4)的总辐射速率以及辐射寿命列在表4中.可以看出当ν′=0时,本文计算的A2Π态的辐射寿命为239.2 ns,与Nguyen等[1]的计算结果误差只有不到1%.随着A2Π态振动量子数的增加,其辐射寿命呈增加趋势.B2Σ+态的自发辐射分为两种情况,即B2Σ+→X2Σ+和B2Σ+→A2Π跃迁.从表3中可以看出B2Σ+→A2Π跃迁的总辐射速率大约只有B2Σ+→X2Σ+跃迁的总辐射速率的1/104倍,因此我们在计算B2Σ+态的自发辐射时间时可以只考虑B2Σ+→A2Π跃迁的辐射速率,本文预测B2Σ+态的辐射寿命为431.2 ns,随着B2Σ+态振动量子数的增加,其辐射寿命呈减小趋势.

3.3 SOC效应对激光冷却BH+离子的影响

由于BH+离子的A2Π和B2Σ+态大约在2.7 Å发生了交叉,从图1(b)中可以看出A2Π态的势能曲线在5.0 Å左右才开始趋于解离,两个电子态相交在弗兰克-康登区域.考虑SOC效应时,A2Π态的1/2分量和B2Σ+态的1/2分量必然会避免交叉.为了讨论这种避免交叉给激光冷却BH+离子带来的影响,我们在相同水平下考虑SOC效应计算了X2Σ+,A2Π和B2Σ+态的势能曲线及跃迁偶极矩,并重新评估激光冷却的两个必要条件:弗兰克-康登因子及辐射寿命.

图3 BH+离子Ω态的势能曲线Fig.3.Potential energy curves for the Ω states of BH+.

BH+离子的和态的势能曲线见图3.采用M-S函数拟合得到了A2Π1/2和A2Π3/2态的光谱常数,对于A2Π1/2态,Re=1.24756 Å,ωe=2250.29 cm−1和ωeχe=54.62 cm−1; 对于A2Π3/2态,Re=1.24756 Å,ωe=2248.17 cm−1和ωeχe=52.27 cm−1. 由于A2Π1/2和态在2.7 Å出现了避免交叉导致了A2Π1/2态的曲线平滑度变差,SOC效应对A2Π1/2态的光谱常数的影响比对A2Π3/2态的影响要显著,尤其是非谐振频率.

4 结 论

本文利用MRCI+Q方法,采用ACV5ZDK全电子基组计算了BH+离子前4个离解通道B+(1Sg)+H(2Sg),B+(3Pu)+H(2Sg),B(2Pu)+H+(1Sg)和B+(1Pu)+H(2Sg)的9个Λ—S电子态的势能曲线.采用M-S函数拟合得到了每个电子态的光谱常数.本文计算的X2Σ+,A2Π和B2Σ+态的光谱常数和已有实验值符合得很好.A2Π和B2Σ+态的势能曲线在2.7 Å出现交叉.b4Σ+,32Σ+,32Π和42Σ+态的光谱常数为首次报道,32Π和42Σ+态具有双势阱结构.采用LEVEL8.0程序分别计算得到了A2Π和B2Σ+态的自发辐射寿命:τ(A2Π)=239.2 ns和τ(B2Σ+)=431.2 ns.最后在考虑SOC效应情况下得到A2Π1/2态的辐射寿命为239 ns.SOC效应对激光冷却BH+离子的影响很小.

[1]Nguyen J H V,Viteri C R,Hohenstein E G,Scherrill C D,Brown K R,Odom B 2011New J.Phys.13 063023

[2]Li Y C,Meng T F,Li C L,Qiu X B,He X H,Yang W,Guo M J,Lai Y Z,Wei J L,Zhao Y T 2017Acta Phys.Sin.66 163101(in Chinese)[李亚超,孟腾飞,李传亮,邱选兵,和小虎,杨雯,郭苗军,赖云忠,魏计林,赵延霆2017物理学报66 163101]

[3]Kusunoki I 1984Chem.Phys.Lett.105 175

[4]Almy G M,Horsfall Jr R B 1937Phys.Rev.51 491

[5]Bauer S H,Herzberg G,Johns J W C 1964J.Mol.Spectrosc.13 256

[6]Ottinger C,Reichmuth J 1981J.Chem.Phys.74 928

[7]Ramsay D A,Sarre P J 1982J.Chem.Soc.:Faraday Trans.78 1331

[8]Viteri C R,Gilkison A T,Rixon S J,Grant E R 2006J.Chem.Phys.124 144312

[9]Rosmus P,Meyer W 1977J.Chem.Phys.66 13

[10]Guest M F,Hirst D M 1981Chem.Phys.Lett.80 131

[11]Klein R,Rosmus P,Werner H J 1982J.Chem.Phys.77 3559

[12]Werner H J,Knowles P J,Lindh R,et al.M O L P R O,version 20101,a package ofab initioprograms,2010,see http://www.molpro.net

[13]Roothaan C C J 1960Rev.Mod.Phys.32 179

[14]Knowles P J,Werner H J 1985J.Chem.Phys.82 5053

[15]Knowles P J,Werner H J 1985Chem.Phys.Lett.115 259

[16]Werner H J,Knowles P J 1988J.Chem.Phys.89 5803

[17]Knowles P J Werner H J 1988Chem.Phys.Lett.145 514

[18]Berning A,Schweizer M,Werner H J,Knowles P J,Palmieri P 2000Mol.Phys.98 1823

[19]Woon D E,Dunning Jr T H 1995J.Chem.Phys.103 4572

[20]Dunning Jr T H 1989J.Chem.Phys.90 1007

[21]Murrell J N,Sorbie K S 1974J.Chem.Soc.:Faraday Trans.70 1552

[22]LeRoyR JLevel80: A ComputerProgram forSolving the RadialSchrödingerEquation for Bound and Quasibound Levels,University of Waterloo Chemical Physics Research Report CP-663 See http://leroy.uwaterloo.ca/programs

[23]Moore B C 1971Atomic Energy Levels(Vol.1)Natl.Stand Ref.Data Ser.Natl.Bur.Stand.No.35(Washington,DC:U.S.GPO)pp1–2 and 16–19

[24]Huber K P,Herzberg G 1979Molecular Spectra and Molecular Structure,Constants of Diatomic Molecules(Vol.4)(New York:van Nostrand Reinhold)p90

[25]Wang X Q,Yang C L,Su T,Wang M S 2009Acta Phys.Sin.58 6873(in Chinese)[王新强,杨传路,苏涛,王美山2009物理学报58 6873]