基于自准直效应的光子晶体异质结偏振分束器∗

左依凡 李培丽 栾开智 王磊

(南京邮电大学光电工程学院,南京 210023)

1 引 言

偏振分束器是光学系统中的一种重要器件,能够将电磁波相互正交的两种偏振模式分离并沿不同方向传播.传统的偏振分束器[1,2]一般基于多层膜结构或晶体的双折射特性,其尺寸一般在毫米量级,主要依赖布儒斯特角进行分束,对角度依赖非常敏感,且透射光的消光比不高,难以满足现代光集成系统的需要,因此需设计更高效紧凑的偏振分束器.近年来,光子晶体由于具有操控光子运动的能力[3]得到更多的关注,基于光子晶体设计的偏振分束器已有较多相关报道.

2008年,沈鹏等[4]设计了一种基于光子晶体自准直效应的复合结构的光子晶体分束器,可实现频率0.268—0.278(c/a)内横电(TE)和横磁(TM)模的分束,透射率为85%且消光比分别为23.03 dB和15.54 dB,具有较大的分束角和分束率,但消光比不够高;2010年,孙露露等[5]设计了一种基于GaAs材料的光子晶体偏振分束器,该分束器使得TE模处于正折射,TM模处于负折射,二者出射时形成一定角度实现偏振分离.该器件的入射波角度在20°以内变化,对分离效果影响程度较小,但需引入消反层才能降低反射率增加透过率,设计较为复杂;同年,郭浩等[6]基于光波在直波导和复合结构光子晶体中的传播特性提出了一种三角晶格的光子晶体分束器,根据TE和TM模式光子禁带的位置彼此错开进行分束,实现了TE和TM模的120°角度分离,但分束器的尺寸及透射率还有改善的空间;2011年,张旋等[7]提出了一种基于二维光子晶体完全禁带内单片真态波导结构的超微偏振分束器,在特定频率0.4194(a/λ)处实现两偏振态的分离,消光比为21.4 dB,但需要引入三个缺陷孔才能导出TE波,结构复杂且透射率较低;2013年,周飞等[8]根据不同禁带范围的特性,设计了一种光子晶体偏振分束器,其尺寸小,透射率为92%,但TM模波的消光比仅为13.3 dB;2014年,Bagci等[9]设计了基于自准直效应的具有复合结构的偏振分束器,该结构以AlxGa1−xAs为基底,TE和TM模的透过率均为75%以上,但该透过率还可以进一步的提高;2016年,Noori等[10]设计了一种具有消反层的二维空气孔排列的偏振分束器,TE和TM模偏振光消光比分别为70 dB和12 dB,但是TE偏振光的一部分已经扩散到TM模端口,导致TM模端口的低消光比,且结构过于复杂.

本文基于光子晶体的自准直效应[11−17]和禁带特性,提出了一种光子晶体异质结偏振分束器,该结构是由两个晶格常数相同、空气孔半径不同的二维正方晶格光子晶体拼接而成,光波无衍射地准直传输并在分界面处实现了TE和TM模式偏振分离.利用自准直效应可控制光的传输,实现波导一般的导光,且不需要额外引入缺陷,可大大降低制作难度.利用Rsoft软件对提出的光子晶体偏振分束器的分束特性进行了仿真分析,并结合平面波展开和时域有限差分两种方法[18]对分束器的透射率、偏振消光比等性能进行了研究.

2 结构设计及原理

光子晶体异质结偏振分束器的结构如图1所示.该结构是在高折射率介质(Si,n=3.42)中引入22×21的正方晶格空气孔体系,由Γ—X方向的对角线将该正方晶格分为左下三角区光子晶体PC1和右上三角区光子晶体PC2.PC1的空气孔半径R1=1/3a,PC2的空气孔半径R2=0.4a,a为晶格常数,四周设有完美匹配层.

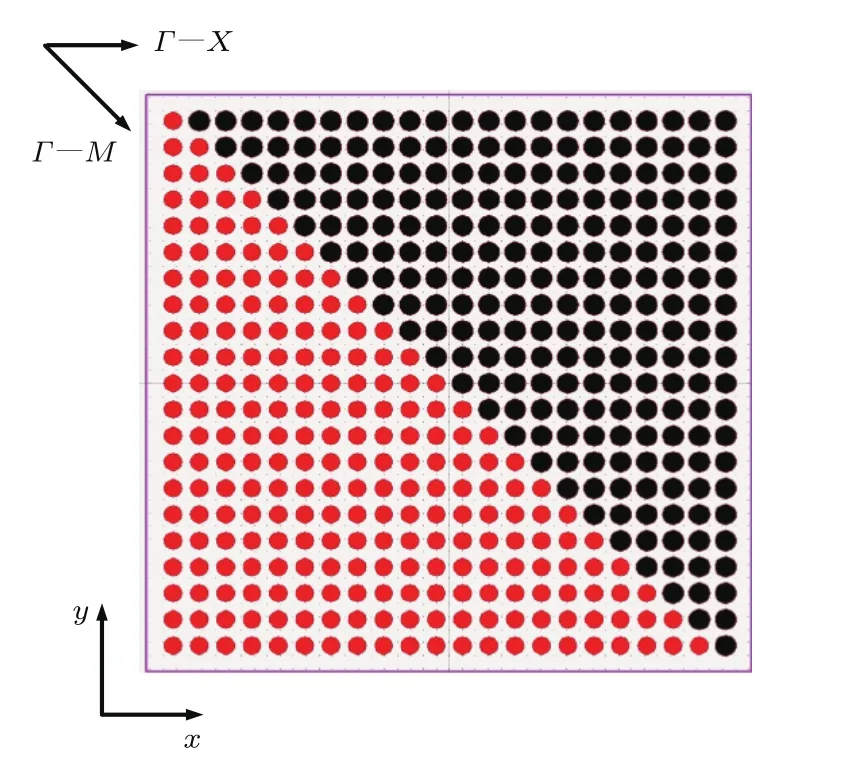
图1 基于自准直效应的光子晶体异质结偏振分束器结构Fig.1.Structure of photonic crystal heterojunction polarization beam splitter based on self-collimation.

在PC1中,结合能带结构图和等频图分析光波的传播.利用平面波展开法可以得到PC1的能带结构图,进而得出TE和TM模均在导带内的频率范围.PC1的能带图如图2所示,可知导带归一化频率范围为0—0.33(a/λ).

图2 光子晶体PC1的能带结构图Fig.2.Band structure of photonic crystal PC1.

利用平面波展开可以得到光子晶体PC1的等频面图,确定TE和TM模均可无衍射传输的光波频率.在光子晶体中,光波总是沿着垂直于等频面的方向传输,如果等频面在很大的张角范围内都是平坦的直线,则此频率区间内的光波在光子晶体传输时,只存在于垂直于等频面这一方向,所以光束仅沿此方向传输,即发生了自准直效应.光子晶体PC1中的TE和TM模的等频面图如图3(a)和图3(b).当归一化频率在0.267—0.285(a/λ)时,TE和TM模的等频线都是环绕Γ点的圆角正方形,平坦的等频线表明TE和TM模均可在该结构中沿Γ—X方向无发散地准直传输.

光子晶体PC2能带结构如图4所示.由图4可知:频率0.263—0.287(a/λ)和0.37—0.42(a/λ)为TM模的光子带隙,TM模不能通过;TE模一直是导通的,即在频率范围为0—0.33(a/λ)内也是导通的.图5给出了光子晶体PC2的TE模的第二能带等频面图,当频率在0.275—0.3097(a/λ)中,TE模可在PC2中沿Γ—X方向无发散地准直传输.

在此偏振分束器结构中,由于交界面与入射光方向夹角为45°,是一种非正交异质结结构,因此结构简单更易制备.在频率0.275—0.285(a/λ)内,电磁波在光子晶体PC1中可以准直无衍射地传输,在交界面处实现两种偏振模式的分离;TE模经交界面进入光子晶体PC2中以很小的角度偏转透射继续准直无发散地传输,TM模则由于在PC2中处于禁带不能通过,在交界面处反射到与入射垂直的方向.

图3 光子晶体PC1中,(a)TE模的等频面图和(b)TM模的等频面图Fig.3.(a)Curves of equal frequency for TE mode and(b)curves of equal frequency for TM mode in photonic crystal PC1.

图4 光子晶体PC2的能带图Fig.4.Band structure of photonic crystal PC2.

图5 光子晶体PC2中TE模的等频面图Fig.5.Curves of equal frequency for TE mode in photonic crystal PC2.

3 结果分析

利用时域有限差分法仿真模拟了TE和TM模两种偏振模式在该偏振分束器中的传播和分束.左侧用一4a高斯光束垂直入射,在自准直频率范围中选取归一化频率为0.28(a/λ).TE和TM模的稳态场分布如图6所示.从图6(a)可以看出,TE模是在PC1中准直传输,经交界面发生了微小角度的偏转进入PC2继续无衍射地传输;从图6(b)可以看出,TM模在PC1中准直传输经交界面发生了90°反射,从而实现了两种偏振模式的分离.

图6(a)TE模的稳态场分布;(b)TM模的稳态场分布Fig.6.(a)Distribution of electromagnetic field of TE mode;(b)distribution of electromagnetic field of TM mode.

3.1 TE和TM模的透过率

利用Rsoft软件仿真分析电磁波的传输行为时,在偏振分束器的入射端和两个出射端分别放置三个相同的探测器,记录入射光和出射光的强度,从而通过出射端与入射端的比值得到TE和TM模输出的透射率.在自准直频率范围0.275—0.285(a/λ)内,TE和TM模输出端的透过率如图7所示.由图7可知,TE模的透过率随着频率的增加而不断降低,TM模透过率随频率的增加而升高,两者的透过率均在88%以上.两者的最高透过率分别可高达94%和93.75%.

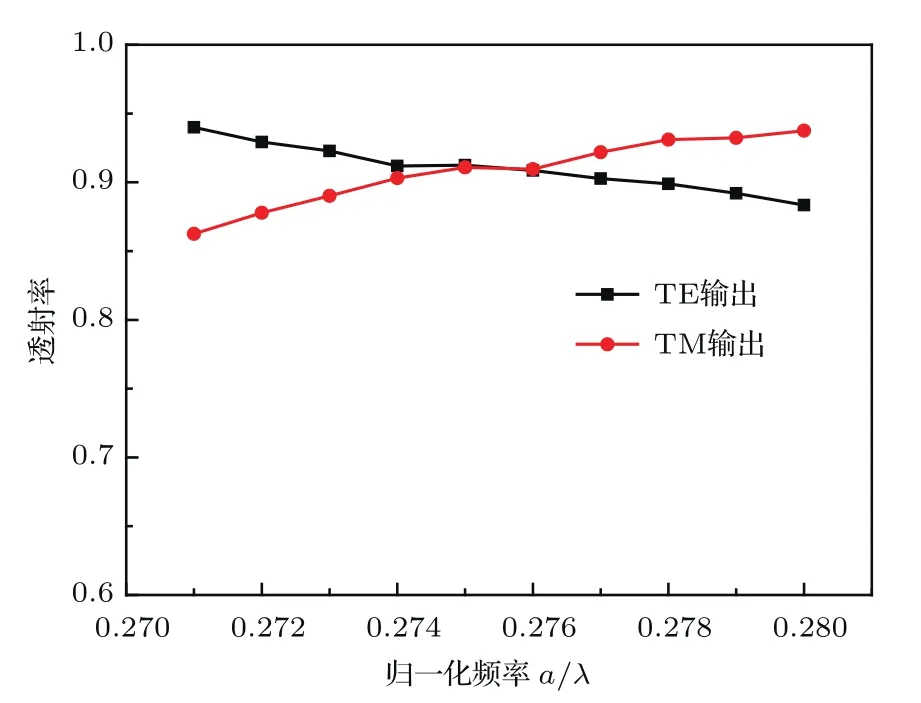
图7 TE,TM模透射率随频率的变化Fig.7.Transmittance of TE and TM modes varying with frequency.

3.2 分离度

除了透过率这个参数需要定量研究之外,分离度也是偏振分束器一个重要参数.偏振模的分离程度可用消光比来衡量.TE模输出端的偏振消光比[19]定义为

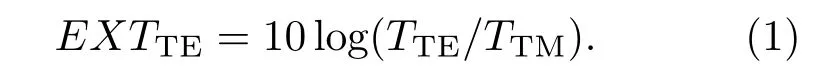
TM模输出端的偏振消光比为

这里,TTE,TTM分别为透射的TE和TM模的强度,RTM,RTE分别为反射的TM和TE模的强度.

偏振分束器两输出端口在工作范围内的消光比如图8所示.从图8可知,随着频率的增加,TE模的偏振消光比从28.61 dB缓慢降低至26.57 dB;TM模的偏振消光比从17.50 dB缓慢增加到18.04 dB.可看出,TE和TM模的消光比在这段频率中变化很小,基本平行于x轴,其中TE和TM模的消光比最大分别为28.61和18.04 dB.

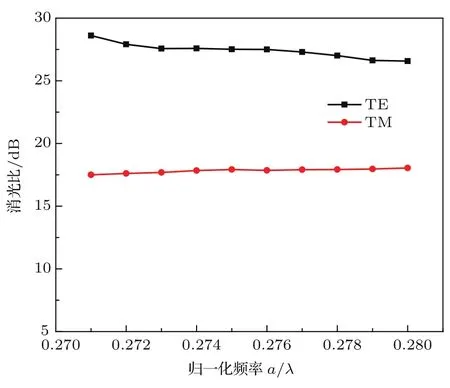
图8 TE,TM模输出端的消光比随频率的变化Fig.8.Exinction ratio of TE and TM modes varying with frequency.

这种偏振分束器可应用到太赫兹波段的传输系统中,选取a=26µm,R1=8.667µm,R2=10.4µm,尺寸大小为572µm×546µm,在91—95µm波长范围(频率为3.158—3.296 THz)内其可实现TE和TM模的分离.因此,此偏振分束器可以在很小的尺寸上实现TE,TM模偏振模式的传输和分束,并在较大的频率范围内(0.275—0.285(a/λ))保持较高的透过率和偏振消光比.

利用这种基于自准直效应的光子晶体异质结结构也可以设计用于光通信波段的偏振分束器.在光通信波段中,硅的折射率n=3.48,设计晶格常数a=426.25 nm,可得到R1=142 nm,R2=170.5 nm,该偏振分束器的大小仅为9.38µm×8.95µm.通过平面波展开和二维时域有限差分法研究表明,在1511—1579 nm波长范围内均可实现偏振分离,其TE和TM模透过率均在88%以上,最高透过率分别可高达94.08%和96.30%;TE和TM模的消光比在这段频率中变化很小,基本平行于x轴,其中TE和TM模的消光比分别大于28和16.62 dB,最大分别为29.98和17 dB.

4 结 论

本文将光子晶体的自准直效应和禁带特性相结合,利用平面波展开法和时域有限差分法,设计了一种具有非正交异质结结构的偏振分束器,在无需引入缺陷或波导的情况下,可以使光波在该结构中准直无发散的传输并实现分束功能,对制造工艺的要求大大降低,更易制作.研究结果表明,设计的偏振分束器在频率范围f=0.275—0.285(a/λ)内,TE和TM模的透过率均在88%以上,偏振消光比分别大于26.57和17.50 dB,有效地实现了TE和TM模的大角度偏振分离.若a=26µm,尺寸大小为572µm×546µm,在太赫兹波段91—95µm波长范围内可实现TE和TM模的分离.利用该结构可设计用于光通信系统中的偏振分束器,n=3.48,a=426.25 nm,尺寸仅为9.38µm×8.95µm,在光通信波段1511—1579 nm波长范围内均可实现偏振分离.本方案结构简单,易于集成,在未来的集成光路中具有很好的应用前景.

[1]Galan J V,Sanchis P,Garcia J,Blasco J,Martinez A,Martí J 2009 Appl.Opt.48 2693

[2]Lee B,Jung J,Han K J,Yong W L 2003 Opt.Express 11 3359

[3]Edition S 1995 Photonic Crystals:Molding the Flow of Light(Princeton:Princeton University Press)

[4]Shen X P,Han K,Li H P,Shen Y F,Wang Z Y 2008 Acta Phys.Sin.57 1737(in Chinese)[沈晓鹏,韩奎,李海鹏,沈义峰,王子煜2008物理学报57 1737]

[5]Sun L L,Shen Y F,Wang J,Zhou J,Zhang Y,Tang G 2010 Acta Photon.Sin.39 1795(in Chinese)[孙露露,沈义峰,王娟,周杰,张园,唐刚2010光子学报39 1795]

[6]Guo H,Wu P,Yu T B,Liao Q H,Liu N H,Huang Y Z 2010 Acta Phys.Sin.59 5547(in Chinese)[郭浩,吴评,于天宝,廖清华,刘念华,黄永箴2010物理学报59 5547]

[7]Zhang X,Liao Q H,Chen S W,Hu P,Yu T B,Liu N H 2011 Acta Phys.Sin.60 104215(in Chinese)[张旋,廖清华,陈淑文,胡萍,于天宝,刘念华 2011物理学报 60 104215]

[8]Zhou F,Fei H M,Chen Z H,Liu X,Yang Y B 2013 Laser Optoelectr.Prog.50 158(in Chinese)[周飞,费宏明,陈智辉,刘欣,杨毅彪 2013激光与光电子学进展 50 158]

[9]Bagci F,Can S,Akaoglu B,Yilmaz A E 2014 Radioengineering 23 1033

[10]Noori M,Soroosh M,Baghban H 2017 J.Mod.Opt.64 491

[11]Kosaka H,Kawashima T,Tomita A,Notomi M,Tamamura T,Sato T 1999 Appl.Phys.Lett.74 1370

[12]Witzens J,Loncar M,Scherer A 2002 IEEE J.Sel.Top.Quant.8 1246

[13]Chen C,Sharkawy A,Pustai D,Shi S,Prather D 2003 Opt.Express 11 3153

[14]Yu X F,Fan S H 2003 Appl.Phys.Lett.83 3251

[15]Li Y Y,Gu P F,Li M Y,Zhang J L,Liu X 2006 Acta Phys.Sin.55 2596(in Chinese)[厉以宇,顾培夫,李明宇,张锦龙,刘旭2006物理学报55 2596]

[16]Tong X,Han K,Shen X P,Wu Q H,Zhou F,Ge Y 2011 Acta Phys.Sin.60 064217(in Chinese)[童星,韩奎,沈晓鹏,吴琼华,周菲,葛阳2011物理学报60 064217]

[17]Liao W Y,Zhang Y X,Chen W H 2015 Acta Phys.Sin.64 064209(in Chinese)[梁文耀,张玉霞,陈武喝 2015物理学报64 064209]

[18]Johnson S G,Joannopoulos J D 2001 Opt.Express 8 173

[19]Chen H,Xu Y,He J,Hong Z 2009 Opt.Commun.282 3626