快速空间测角系统中偏振像差的分析与研究∗
李春艳 陆卫国 乔琳
1)(西安邮电大学电子工程学院光电子技术系,西安 710121)
2)(中国科学院西安光学精密机械研究所,西安 710119)
1 引 言
基于偏振光和磁光调制的空间角度精密测量及传递技术目前已广泛应用于火箭与导弹发射、航天器对接、玻璃内应力测量等装置,相比机械和其他几何光学方法,该方法具有不需要刚性连接、方位传递距离远、测量精度高等特点[1−4].而这种基于偏振棱镜正交消光原理的方位信息测量方式需要复杂的伺服跟踪系统辅助,测量时间较长,降低了系统的可靠性及反应灵敏性[5−11].为提高系统的测量精度及快速反应能力,学者们提出了基于Wollaston棱镜偏振分束的快速空间测角方法,根据两路光强大小直接解算出方位角,缩短了测量时间,并通过采用磁光调制技术,提高测量精度[12−14].而快速空间测角系统的下端信号接收单元需要在一定的平移范围内实现角度测量,受偏振棱镜、磁光玻璃尺寸及系统体积和成本所限,为实现大范围区域内的测量功能并满足性能要求,选择对入射至偏振棱镜的光进行扩束,因此进入起偏器的光束为非垂直入射光.而所有的光学界面都会使非正入射光波的偏振态发生变化,存在偏振像差[15−24],所以快速空间测角系统中非准直光的入射必然会影响到光的偏振态,从而影响系统的角度传递测量精度.针对此问题,本文采用偏振光线追迹的方法,结合电磁场的边界条件推导了快速空间测角系统中光束通过偏振棱镜后出射光束的偏振态变化及分布,并运用Matlab软件进行了仿真分析;最后通过搭建实验平台,根据平移偏振光接收及处理单元模拟不同的入射方位及角度变化,获得测量方位值,并将其与对中状态下所测量的方位值做对比,得出偏振像差的存在对测角精度的影响,验证了理论分析的正确性.研究结果对优化系统结构并进一步提高系统性能具有一定的指导意义.
2 快速空间测角系统工作原理
快速空间测角系统的工作原理如图1所示.带有扩束镜BE的激光光源L发出的光束通过透光轴在y方向的起偏器P形成线偏振光,线偏振光通过光轴与y方向夹角约为45°的Wollaston棱镜W分成两束偏振方向相互垂直的线偏振光,分别到达光电探测器De和Do,利用后续信号处理电路对光电探测器接收到的信号进行处理,即可解算出Wollaston棱镜光轴偏离45°角的方位角δ[12,14].
δ是利用获得的两路信号光强实时地解算出来的,

式中,Ie,Io分别为两出射光束的光强.

图1 快速空间测角系统工作原理图Fig.1.Working principle of rapid spatial azimuth measurement system.
3 偏振像差对系统测角精度的影响分析
快速空间测角系统采用Glan-Taylor棱镜作为起偏器,与Wollaston棱镜不同的是,Glan-Taylor棱镜的两部分晶体光轴相互平行,且两晶体之间为空气间隙.从Glan-Taylor棱镜出射的为e光(非寻常光),而o光(寻常光)在棱镜的斜面全反射,从棱镜侧面射出.因此为讨论方便,忽略o光和空气间隙,研究在一定入射角和方位角范围内,从Glan-Taylor棱镜出射光束的偏振态变化[25−29].
如图2所示,坐标o-xyz的原点位于晶体的第一表面的中心,xy在第一表面内,且y轴与光轴平行,z轴正方向为法线方向.设入射光在第一表面的入射角为θ,ϕ为入射面与y轴正向所成的方位角.设i,j,k分别代表x,y,z方向的单位矢量,由此,入射光方向矢量可以表示为e0=sinϕsinθi+cosϕsinθj+cosθk,其中光轴方向为e=j.取晶体外的折射率n=1,经过第一表面后,e光的折射角为θe1,因此e光波的矢量可以表示为ee1=sinϕsinθe1i+cosϕsinθe1j+cosθe1k.其中θe1根据折射定律获得:

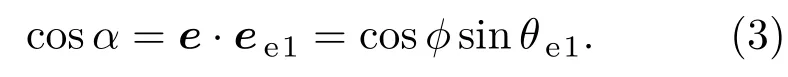
由(2)和(3)式可得


图2 光线在Glan-Taylor棱镜中的传播Fig.2.Light propagation in Glan-Taylor prism.
设入射光的磁场强度H1的单位矢量为h1,h1垂直于e光主平面,则h1=(e×ee1)/sinα,设e光线单位矢量为k1r,k1r与光轴的夹角θrp即可表示为设e光波与e光线的离散角为ψ1= θrp−α,则e光线的折射率为,h1垂直于入射e光的主平面,有,令k1r=ai+bj+ck,结合h1及k1r与光轴的夹角θrp,可得e光线方向的表达式并化为单位矢量为
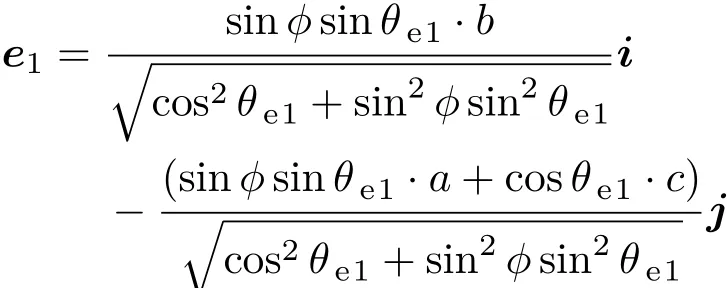
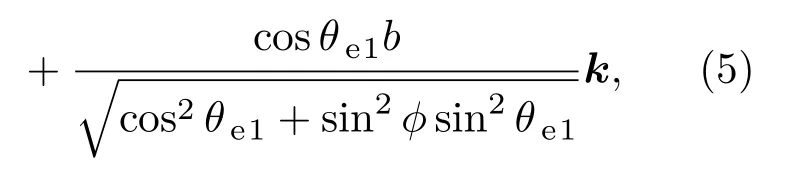
式中

根据折射定律ne1sinθe1=nosinβo=ntsinβe=sinθ2,则反射的o光与e光的方向分别为
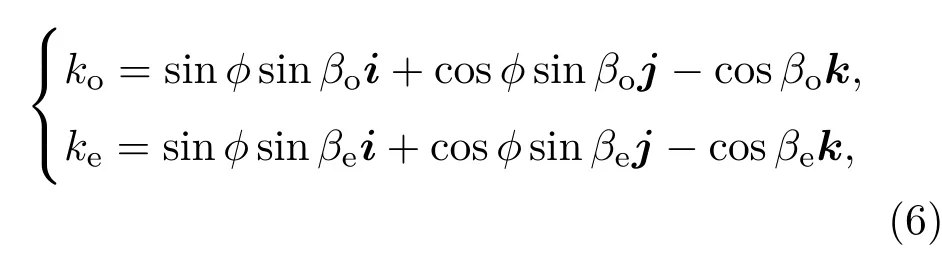
式中
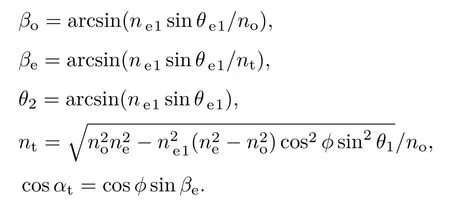
反射o光的电场强度Eo的单位矢量为eo,则eo垂直于o光主平面,为

对应磁场强度Ho的单位矢量ho=ko×eo,可表示为
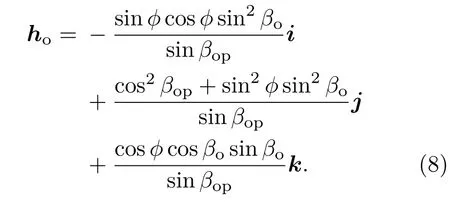
设反射e光的磁场强度He的单位矢量为he,垂直于e光主平面,得
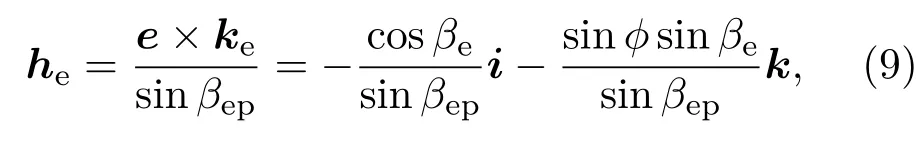
式中βep=arccos(cosϕsinβe)为e光波与光轴的夹角,设反射e光线的单位矢量为kr,由磁场强度垂直于e光主平面,则he=(e×kr)/sinβrp.设kr=di+ej+fk,两端同时右边叉乘e,得
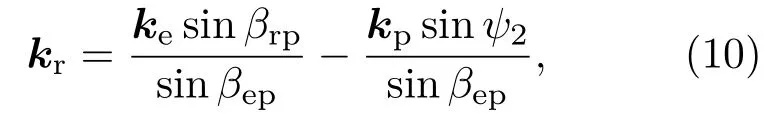
式中

则电场强度单位矢量为

从Glan-Taylor棱镜出射的e光折射光的波矢方向为

假设出射光电场强度E2的单位矢量为e2=a1i+a2j+a3k,则出射光的磁场方向:

由晶体表面的边界条件E1t+Eot+Eet=E2t,H1t+Hot+Het=H2t,将其按x,y方向可表示为
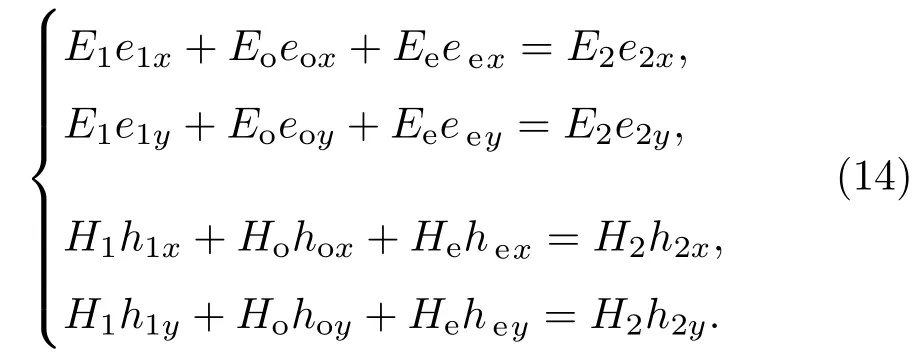


(16)式中,


图3 不同入射角θ下Glan-Taylor棱镜出射光的偏振方向改变量(a)−3°≤ θ≤ 3°;(b)−2°≤ θ≤ 2°;(c)−0.8°≤ θ≤0.8°;(d)−0.4°≤θ≤0.4°Fig.3.Polarization change of light from the Glan-Taylor prism under different incidence angles:(a) −3°≤θ≤3°;(b)−2°≤θ≤2°;(c)−0.8°≤θ≤0.8°;(d)−0.4°≤θ≤0.4°.
则出射光E2在xy平面的投影向量与光轴的夹角即为偏振方向的改变量Δ,即
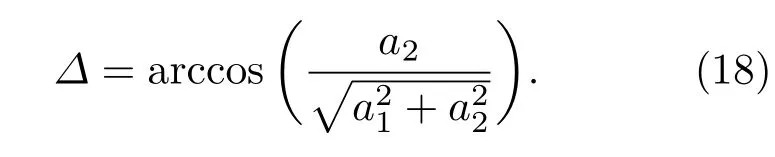
取Glan-Taylor棱镜的折射率no=1.656,ne=1.485,半视场角≤ 3.5°,对不同入射角度下出射光偏振态的改变量进行Matlab仿真,仿真结果如图3所示.
图3为不同入射角下Glan-Taylor棱镜出射光的偏振方向改变量.由以上仿真结果可以看出,当方位角ϕ=0°时,出射偏振光的偏转方向为零,当ϕ=90°时,出射偏振光的偏转方向最大,且随入射角的增大,偏转角度也增大,当入射角为3°时,偏转角度将大于100°.
4 实验与讨论
为验证理论分析的正确性,通过搭建实验平台,进行了相关实验.测量系统工作原理如图4.
由图4可知,实验装置基于偏振分束的快速空间角度测量原理并采用磁光调制技术,实验时为便于虚拟方位信息的引出测量,在偏振光接收与测量单元增加直角棱镜,并利用自准直经纬仪间接测量方位角[30].系统中光源至偏振光接收与测量单元的距离约为1.4 m;光源经过扩束镜后以发散光的形式进入起偏器,光束口径为5 mm,发散角约为6.5°,且起偏器出射光束中心与系统光轴重合;通过平移接收单元来模拟不同的入射方位及角度变化,具体为分别在同一方位方向下平移接收单元至东、西、南、北、东南、西南、西北、东北八个方向,然后分别在八个方向测得方位值δ,每个方向均测量多组数据,取其平均值与对中情况下(接收单元通光孔中心与铅垂方向重合)的方位均值进行比较,得到偏差值Δ,Δ即为不同方位及入射角情况下系统的测量误差.其中自准直经纬仪通过直角棱镜对接收单元进行监视,保证接收单元在同一个方位下进行平移.八个方向的平移量分别为20,10 mm,折算成光源入射至检偏器的入射角分别约为0.8°,0.4°,具体平移位置如图4(b)所示.实验测量数据如表1所列,其中每次平移均取三组测量值.
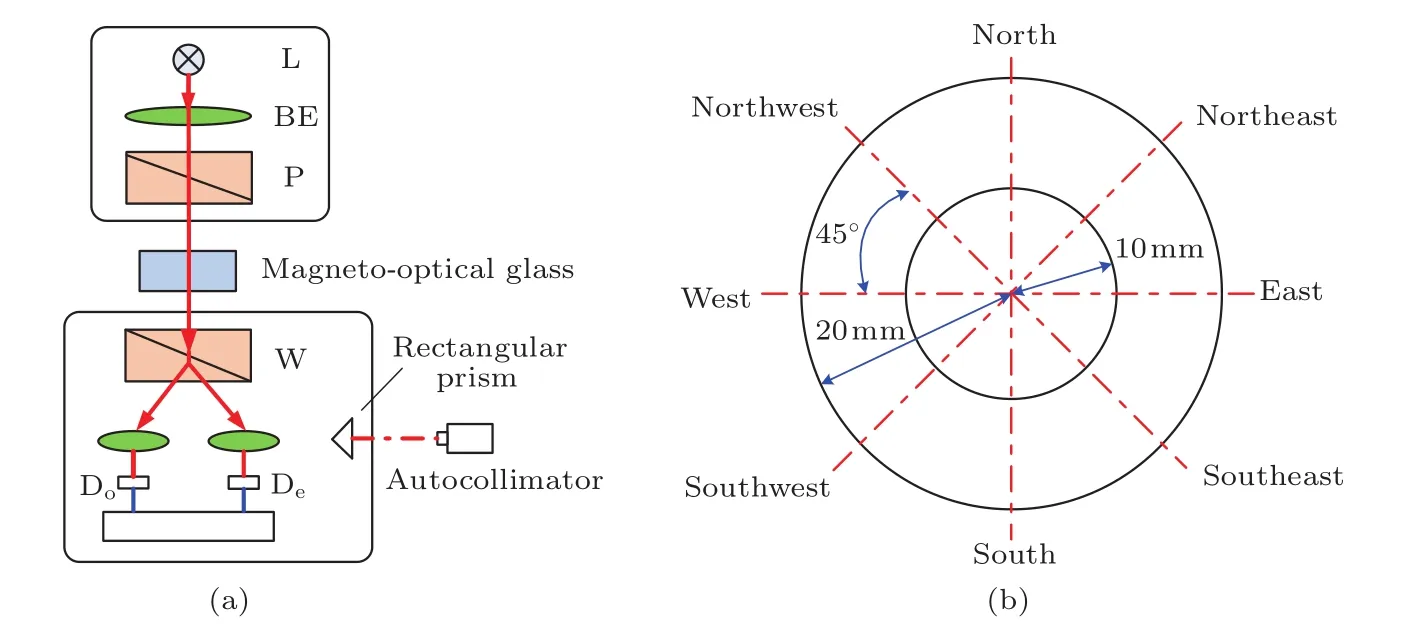
图4 测量系统工作原理图(a)实验装置简图;(b)偏振光接收与测量单元平移位置示意图Fig.4.Working principle diagram of measuring system:(a)Schematic diagram of experimental equipment;(b)translation position of polarized light receiving and measuring unit.
通过表1的实验数据可以看出,在南北方向,即方位角为180°(0°)时,测量偏差值较小,在东西方向,即方位角为90°(270°)时,测量偏差值最大,且随平移距离的增大,测量偏差值也增大.其他方向的测量偏差值处于南北和东西方向之间,表1的测量结果与图3 Glan-Taylor棱镜出射光偏振方向改变量的理论仿真分析结果基本相一致,验证了理论分析的正确性.经过以上理论分析与实验数据可知,出射光偏振方向的改变会对系统测量结果带来较大误差,即在一定的出射光范围内,入射角是影响偏振态变化的主要因素,也是影响系统测角精度的重要因素.
分析以上结果,实际值的变化趋势及范围与理论值相比具有一定的偏差,产生原因可能包括:1)Glan-Taylor棱镜的加工误差,包括两晶体光轴的垂直偏差及光轴与入射端面的角度偏差;2)难以保证光源光束中心、起偏器中心与铅垂方向完全重合,同一直径处的出射角不完全一致;3)实验所采用光源为5 W的半导体耦合激光器,光源本身光束质量及光源噪声等会对实际检测带来一定的影响;4)上述理论分析是针对一定入射角、方位角下单光束的偏振态分布,但实际接收单元有一定的通光孔径,检测到的偏振态是通光孔径范围内偏振态的积分,结果与单光束情况有一定的差别.针对理论仿真及实验现象,可以采取以下措施对系统进行改进设计:1)光源经扩束后,尽量使光束在起偏器、磁光玻璃通光口径范围内,以减少杂光;2)在满足接收平移范围的情况下,光束尽量以一定的小角度入射至起偏器;3)各个视场角的光束尽量以“均匀”的入射角度入射至起偏器.
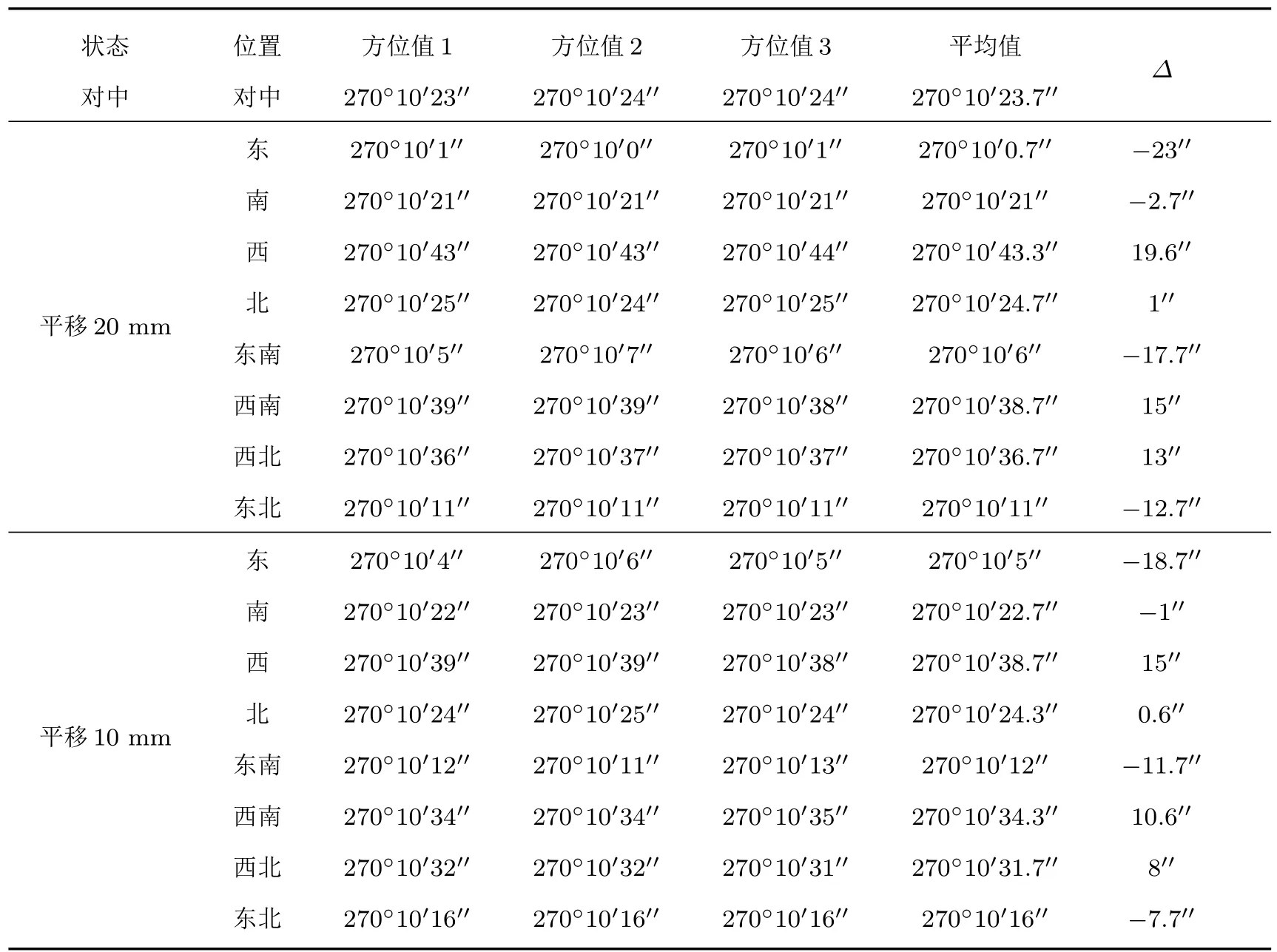
表1 偏振光接收与测量单元在不同位置时的测量方位值Table 1.The azimuth values of polarized light receiving and measuring unit at different positions.
5 结 论
本文根据实际快速空间测角系统在一定的平移范围内均要求实现测量功能的应用需求,研究了光束以一定入射角及方位角经过Glan-Taylor棱镜后出射光束偏振方向的改变,即偏振像差对系统测量结果产生的影响.通过建立坐标系模型,采用偏振光线追迹的方法,结合电磁场的边界条件对快速空间测角系统中光束通过偏振棱镜后出射光束的偏振态变化及分布进行了理论推导,并运用Matlab软件进行了仿真分析,最后根据在测量系统中平移接收单元来模拟不同的入射方位及角度变化,获得测量值,并根据实验值与仿真结果的对比分析,得出偏振像差的存在对测角精度的影响,验证了理论分析的正确性.得出在方位角为0°时,测量误差较小,在方位角为90°时,测量误差最大,且随平移距离(即入射角)的增大,测量误差也增大.针对测量与理论仿真结果的不完全一致,分析了实际测量误差产生的原因,提出了改进措施.该研究对优化系统结构并进一步提高系统性能具有一定的指导意义,对快速空间测角装置的实用化应用具有一定的推进作用.
[1]Dong X N,Gao L M,Shen X J,Chen L Y 2001Acta Phot.Sin.30 1389(in Chinese)[董晓娜,高立民,申小军,陈良益2001光子学报30 1389]
[2]Shen X J,Ma C W,Dong X N 2001 Acta Phot.Sin.30 892(in Chinese)[申小军,马彩文,董晓娜 2001光子学报30 892]
[3]Wu Y M 2009 Ph.D.Dissertation(Xi’an:Xi’an Institute of Optics and Precision Mechanics)(in Chinese)[吴易明2009博士学位论文(西安:西安光学精密机械研究所)]
[4]Wu Y M,Gao L M,Chen L Y 2008 Infrar.Laser Eng.37 525(in Chinese)[吴易明,高立民,陈良益 2008红外与激光工程37 525]
[5]Yang Z H,Huang X X,Zhou Z F,Zhang Z L 2012 Acta Opt.Sin.32 1212006(in Chinese)[杨志勇,黄先祥,周召发,张志利2012光学学报32 1212006]
[6]Yang Z H,Cao W,Wu F C 2015 Acta Opt.Sin.25 s112003(in Chinese)[杨志勇,蔡伟,伍樊成 2015光学学报25 s112003]
[7]Yang Z Y,Huang X X,Zhou Z F,Zhang Z L 2012 Acta Opt.Sin.32 0112006(in Chinese)[杨志勇,黄先祥,周召发,张志利2012光学学报32 0112006]
[8]Yang Z Y,Huang X X,Zhou Z F,Zhang Z L 2012 Acta Opt.Sin.32 1012001(in Chinese)[杨志勇,黄先祥,周召发,张志利2012光学学报32 1012001]
[9]Yang Z Y,Zhou Z F,Zhang Z L 2012 Opt.Precis.Eng.20 692(in Chinese)[杨志勇,周召发,张志利 2012光学20 692]
[10]Shen X,Liang Z C 2014 Optron.Lasers 25 1535(in Chinese)[沈骁,梁忠诚 2014光电子 25 1535]
[11]Yang Z Y,Huang X X,Zhou Z F,Zhang Z L 2011 Acta Opt.Sin.31 1112008(in Chinese)[杨志勇,黄先祥,周召发,张志利2011光学学报31 1112008]
[12]Lu W G,Wu Y M,Gao L M,Xiao M S,Wang H X 2013 Opt.Precis.Eng.21 539(in Chinese)[陆卫国,吴易明,高立民,肖茂森,王海霞2013光学·精密工程21 539]
[13]Lu W G,Wu Y M,Gao L M,Li C Y,Xiao M S 2014 Infrar.Laser Eng.43 2198(in Chinese)[陆卫国,吴易明,高立民,李春艳,肖茂森2014红外与激光工程43 2198]
[14]Lu W G 2013 Ph.D.Dissertation(Xi’an:Xi’an Institute of Optics and Precision Mechanics)(in Chinese)[陆卫国2013博士学位论文(西安:西安光学精密机械研究所)]
[15]Yang Y F,Yan C X,Hu C H,Wu C J 2016 Acta Phot.Sin.36 1106003(in Chinese)[杨宇飞,颜昌翔,胡春晖,吴从均2016光子学报36 1106003]
[16]Li Y H,Hao X,Shi Z Y,Shuai S J,Wang L 2015 Acta Phys.Sin.64 154214(in Chinese)[李旸晖,郝翔,史召邑,帅少杰,王乐2015物理学报64 154214]
[17]Yun G,Crabtree K,Chipman R A 2011 Opt.Lett.36 4062
[18]Xu J,Liu F,Liu J T,Wang J Y,Han P L,Zhou Z H,Shao X P 2016 Acta Phys.Sin.65 134201(in Chinese)[许洁,刘飞,刘杰涛,王娇阳,韩平丽,周淙浩,邵晓鹏 2016物理学报65 134201]
[19]Lam W S T,Chipman R 2015 Appl.Opt.54 3236
[20]Wu H Y,Zhang C M,Zhao B C 2009 Acta Phys.Sin.58 930(in Chinese)[吴海英,张淳民,赵葆常2009物理学报58 930]
[21]Yun G,Crabtree K,Chipman R A 2011 Appl.Opt.50 2855
[22]Zhang M R,He Z Q,Wang T,Tian J S 2017 Acta Phys.Sin.66 084202(in Chinese)[张敏睿,贺正权,汪韬,田进寿2017物理学报66 084202]
[23]Yun G,McClain S C,Chipman R A 2011 Appl.Opt.50 2866
[24]Wu H Y,Zhang C M,Zhao B C 2008 Acta Phys.Sin.57 3499(in Chinese)[吴海英,张淳民,赵葆常 2008物理学报57 3499]
[25]Shen W M,Jin Y X,Shao Z X 2003 Acta Phys.Sin.52 3049(in Chinese)[沈为民,金永兴,邵中兴2003物理学报52 3049]
[26]Zhang C M,Liu N,Wu F Q 2010 Acta Phys.Sin.59 949(in Chinese)[张淳民,刘宁,吴福全2010物理学报59 949]
[27]Wu H Y,Zhang C M,Zhao B C,Li Y C 2009 Acta Phys.Sin.58 1642(in Chinese)[吴海英,张淳民,赵葆常,李英才2009物理学报58 1642]
[28]Liu C,Cen Z F,Li X T,Xu W C,Shang H B,Neng F,Chen L 2012 Acta Phys.Sin.61 134201(in Chinese)[刘超,岑兆丰,李晓彤,许伟才,尚红波,能芬,陈立2012物理学报61 134201]
[29]Mu Y K,Zhang C M,Zhao B C 2009 Acta Phys.Sin.58 3877(in Chinese)[穆延魁,张淳民,赵葆常 2009物理学报58 3877]
[30]Xiao M S,Li C Y,Wu Y M,Lu W G,Wang H X 2015 Infrar.Laser Eng.44 611(in Chinese)[肖茂森,李春艳,吴易明,陆卫国,王海霞2015红外与激光工程44 611]

