基于摄动法的结构疲劳寿命估计方法

麻凯 李鹏

（吉林大学机械科学与工程学院，吉林 长春 130022；吉林大学机械与航空航天工程学院，吉林 长春 130022）

引言

工程实践中，结构的疲劳特性都是离散的统计数据，然后在汇总形成SN曲线。影响结构的疲劳寿命的因素包括：材料的力学特性、环境因素、工况、结构参数等。针对上述这些因素对结构疲劳寿命影响所采用的方法主要是数学中概率统计法。这些影响因素多是随机变量，在工程计算中也这样处理。即在统计计算中，认为它们都是独立变量，这样很多可靠性计算方法都可以使用。提出了将上述非正太分布的因素作为正太分布参数来计算结构疲劳特性中的安全特性和失效标准；则提出更为精确的方法，它使用结构的寿命函数的隐式表达式来进行概率统计计算。当计算的不确定因素较少时，上述提出的概率统计方法的准确性难以保证。因此，这对这样的情况，又进一步提出了分析不确定性结构的疲劳特性指标的区间分析方法——区间估计分析方法，这是基于凸模型理论用于疲劳寿命预测方法和区间理论、概率的混合模型估计结构疲劳寿命计算方法。这些方法统一的有点就是参数的变化幅度不受限制，不需要初始结构的参数精度太高，它对线性模型具有较好的使用性好。但是，这种区间方法对于非线性模型的适用性不强，在不确定度较大时，用区间分析方法给出的结果不能反映区间内的分布特点。为了使它更适用于工程实践中的其他非线性结构的疲劳分析问题，本文因此在上述研究的基础上，将疲劳寿命函数进行一阶Taylor级数展开，然后进一步扩展到二阶，并形成其区间摄动理论方法。该方法具有法优点，可以在已知不确定参数区间范围或界限条件下，给出确定的结构特性疲劳寿命范围，并克服区间法相对于参数变化较大非线性模型失效的情况，具有更广泛的适用性。本文提出了一个算例，将上述摄动分析方法与原有的概率统计方法进行详细比较，结果说明这种区间摄动分析方法对不确定性结构的寿命估计的计算精度更高。

数值算例

疲劳寿命表达式式

其中，A和S分别表示不确定参数，m=3.5为常数。设A和 S 的区间分别为[Ac-2βAc，Ac+2βAc]，[Sc-βSc，Sc+βSc]，其中Ac=9.66×1013，Sc=82.46；设 β 为偏离系数，它是变量。

当区间增大时，即偏离系数，β，也增大，当β设0.06，0.12，1.80，0.20，0.24和0.36时。可以证明如果以Monte—Carlo为基础拟合结果，本文所提出的区间摄动方法所计算得到的结果要好于其他已知方法。表1列出了概率分布为A和S正太分布假设下，用概率分析的中区间分析方法和蒙特卡洛方法计算所得疲劳寿命区间范围N。表2列出了A和S概率分布为均匀分布，用基于概率分析蒙特卡洛方法和本文使用区间摄动方法计算所得疲劳寿命N的区间范围。图1描述了A和S假设为正太分布和均匀分布，分别使用蒙特卡洛方法和文献中区间分析方法和本文方法的计算结果，疲劳寿命曲线N随着偏离系数β的变化而改变。

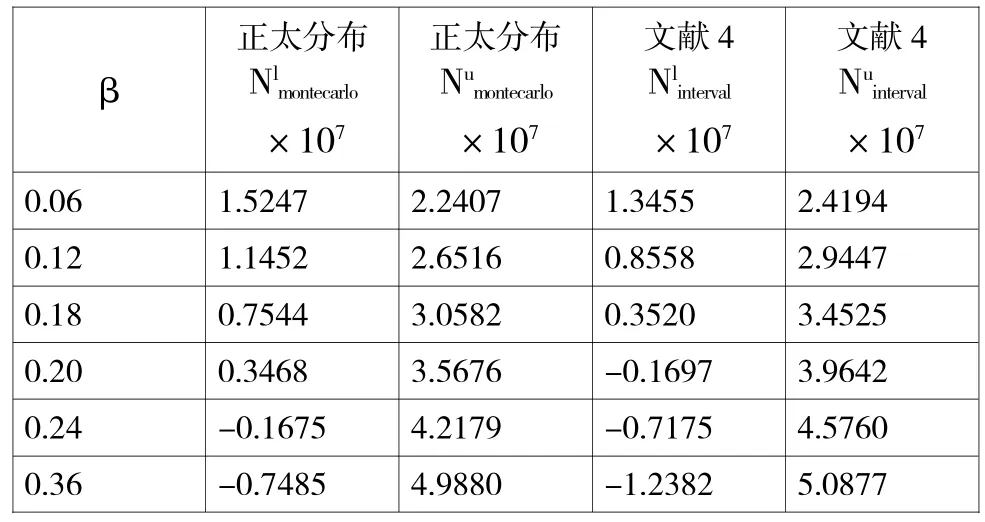
表1 疲劳寿命N范围估计

表2 疲劳寿命N的范围估计

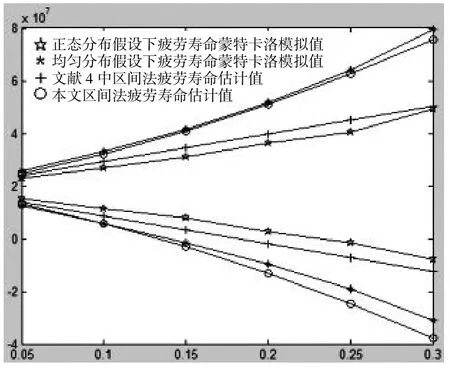
图一

从表1，表2和图一可以得到如下结论：

标准正太分布下，已有区间法和本文方法都有蒙特卡洛模拟的计算结果。通过对比可发现，采用区间方法计算得到区间大小涵盖了分析方法的区间解，当偏离系数值β大于0.4以后，中区间法求得区间上限，不能包括蒙特卡洛法求得区间上限。而根据本文方法，当偏离系数值β大于0.4时仍有效。与文献[4]中算例相比，可以发现这种分析结果与假设的参数概率分布形态十分有关，邱志平在文献[4]中设A在区间内上服从威布尔分布所不同的是，S在其区间内服从最大Ⅰ型极值分布，计算结果是β大于0.3后，用区间计算法得出的结果就不理想了。使用区间法的原因是对结构参数初始条件信息严重缺失，在不清楚变量概率分布形式，只能人为设计。

为了检验更多概率分布条件下有效性，本文假设参数服从均匀概率分布，并比较计算结果从表一，表二和图二可以得到以下结论：

偏离系数值β刚一开始，即发生0.06的摄动量，文献[4]给出的计算结果就已经不准确了。本文的方法很接近蒙特卡洛的计算结果，可见本文方法相对于原有区间法有了更为广范的适用性和准确性。主要体现在：首先，结构参数改变时，计算结果不理想，本文方法仍然可以给出相对可靠的结果；其次，当我们对结构参数做不同概率分布假设时，本文的计算方法可以适用于概率分布假设。

结论

本文采用区间方法对不确定性结构的疲劳寿命进行了研究，提出了区间摄动法。这种方法由于是区间解，因此不需要预先知道方差函数或其它概率等信息仅需要掌握不确定参数的区间大小。而且一定程度上克服了原有方法的缺陷。当结构参数的变化较大时，或者某些概率分布很难做出主观估计是，本文的方法具有更广泛的适用性。这当不了解参数在区间内部属于何种概率分布情况下，得到的区间结果十分精确。通过算例表明，本文方法使用区间方法估算结构的疲劳寿命有更广泛的适用性，且具有计算量小的优点，因此在工程中具有很好应用前景。