“抛物线及其标准方程”教学设计

郝变花

（深圳中学，广东 深圳）

一、教学内容与内容解析

1.教学内容：

（1）抛物线的概念；

（2）抛物线的标准方程.

2.内容解析：

解析几何是17世纪数学发展的重大成果之一，其本质是用代数方法研究几何图形的性质，充分体现了坐标法思想.

抛物线是圆锥曲线的一种，是《普通高中数学课程标准》规定的教学内容.这一内容不仅要求学生掌握抛物线的概念及其标准方程，更重要的是使学生明确曲线与方程的对应关系，掌握求曲线方程的一般过程，体会用方程研究曲线的坐标法思想.

二、教学目标与目标解析

1.教学目标：

（1）从具体问题情境中抽象出研究模型，形成抛物线的概念.

（2）通过建立坐标系，求出抛物线的方程.

（3）体会坐标法的基本思想.

2.目标解析：

抛物线的概念及其方程是本节课应使学生掌握的基本知识，但是依附在这些知识上的坐标法思想却是更为重要的数学内容.因此，我们设计具体的问题情景，不仅又一次让学生经历了数学研究过程中模型提炼的过程，而且更突出了曲线方程在研究曲线及其性质中的重要作用，并使抛物线的概念引出变得自然.

在求抛物线方程的过程中，我们没有先设定如何建立直角坐标系，而是让学生根据自己的理解去完成建立坐标系并求出方程的过程.这样做的目的，不仅是为了获得抛物线的四种不同形式的标准方程，而且可以通过比较不同的建立直角坐标系的方式，使学生体会到利用曲线的对称性建立直角坐标系会使曲线方程最简单，并由此得出建立直角坐标系的一般性原则.

三、教学问题诊断分析

1.人们为什么研究抛物线？如何激起学生的研究兴趣与热情？这是教学中应该考虑的问题.教科书是通过设置“信息技术应用”栏目，让学生由此体会抛物线的生成过程，并由此引出抛物线的概念.尽管这样做会使教学过程通畅，但不容易让学生产生强烈的求知欲.为解决这一教学问题，我们设计了一个具体的问题情境，不仅可以由此激发学生的兴趣，而且又一次使学生经历了抽象概括数学研究问题（探求“平面内到一个定点的距离等于到一条定直线的距离的点的轨迹”）的过程.

2.如何在平面内作出满足条件“到一个定点的距离等于到一条定直线的距离”的点是教学中可能遇上的第二个教学问题.教学中，应启发学生点到直线的距离实际上可以转化为点到点的距离，而平面几何中涉及一个点到另外两个点的距离相等的现象有等腰三角形的两腰、已知线段的垂直平分线，等等.在学生思考的基础上，可引导学生从满足条件的点的几何特征寻求作图过程.

3.学生可能会根据已有经验或预习得知满足条件的点的轨迹是抛物线，但如何使学生认识到这种做法不可靠，不符合数学研究的基本要求，这是教学中须重视的第三个问题.教学中要对学生的想法进行分析评价，使他们回归到用方程进行轨迹判定的思维轨道上来，这也是教学的重点.

4.如何建立直角坐标系？这是第四个教学问题，也是教学的难点.教学中要让学生独立寻求方程，通过比较不同坐标系下所得方程的简单程度，得出建立直角坐标系的一般原则.

四、教学支持条件

1.从方法上讲，椭圆、双曲线的研究过程是研究抛物线的基础，是学生认知与思考的重要支持条件.

2.为了解学生的思考状态，比较并评价学生所获得的结果，需要准备实物投影仪、投影机；为动态演示抛物线的形成过程，需要用到几何画板软件；为便于比较学生所作的图形，需要印制统一的作图纸；为方便纪录学生的不同答案，需准备移动白板、白板书写笔.

五、教学过程设计

［情境］ 边长为L的正方形ABCD内，到中心O的距离小于到边的距离的点所组成的图形记为S，正方形内除S以外的点所组成的图形记为T，你认为S与T哪个面积大？

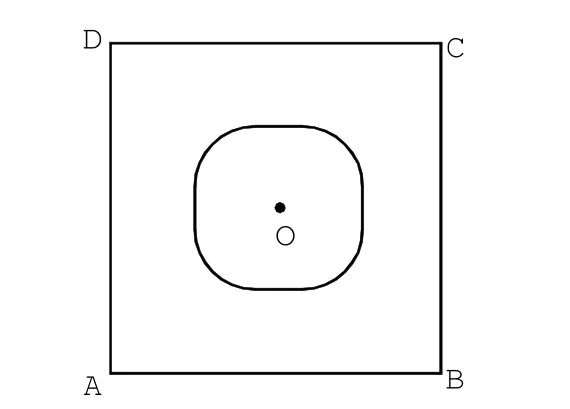
意图：激发学生的研究兴趣，提炼抛物线的研究模型.

师生活动：教师给出问题后让学生思考，使学生明确S与T的边界是解决问题的关键.可让学生猜想边界的形状，并进一步明确S与T的边界上的点应满足几何条件：到中心O的距离等于到相应边的距离.

［问题1］ 在平面内利用尺规作图，你能作出多少个与一个定点F和一条定直线l的距离相等的点？

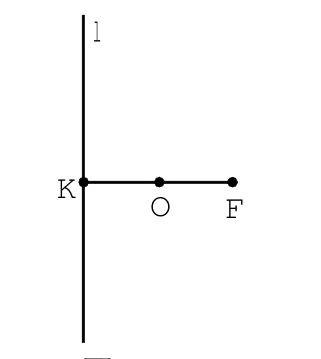
图1

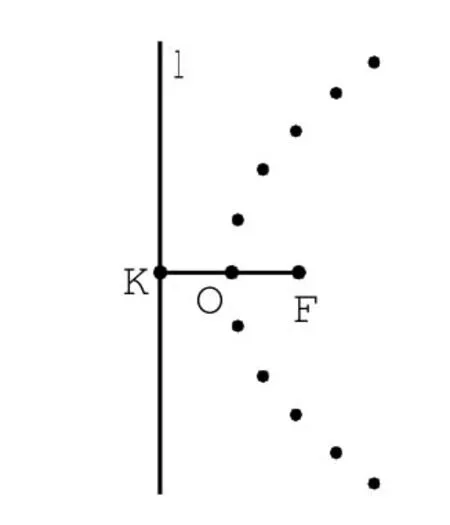
图2

意图：使学生通过画一些具体的点，体会点应满足的几何条件，并为猜测、验证点的轨迹类型提供基础.更重要的是使学生通过“找出一些具体的点，获得作点的一般方法，并由此作出更多的点，从而得出点的轨迹”，体会数学研究的一般过程.

师生活动：让学生作出一些符合条件的点，然后展示学生的作图情况，让学生交流获得点的方法.教师在点评学生作图基础上，总结出一般的作图方法：在直线l上找一个点B，过点B作直线l的垂线，再作线段FB的中垂线，这两条直线相交于点P，点P满足到点F的距离与到直线l的距离相等.教师提出问题：采用这样的方法，我们可以得到多少个符合条件的点？教师用几何画板演示作图过程，得出轨迹的图示.

教师在这里还要提醒学生研究点在直线上的情形（此时动点形成的轨迹是过点且垂直于直线的直线），为后面给出抛物线的定义作准备.

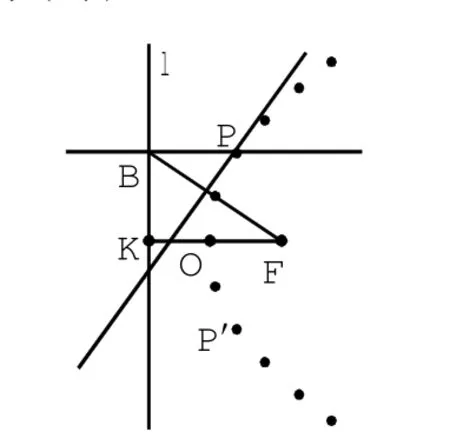
图3

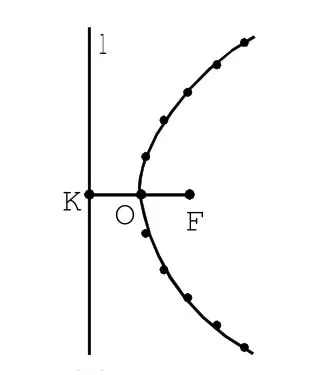
图4

［问题2］ 问题1中的轨迹是什么曲线？你能说说理由吗？

意图：启发学生利用方程研究曲线的性质.

师生活动：让学生回答他们的判断.第一种可能的回答是抛物线.

第二种可能的回答是椭圆的一部分，或双曲线的一部分.

无论哪一种回答，教师都要追问他们为什么，如果学生不能想到用方程来判断轨迹的类型，教师可以给出一些方程让学生想想是什么图形.最后要让学生明确：通过求轨迹的方程，可以判断曲线的类型.

［问题3］ 你会怎样建立直角坐标系，求出问题1中的轨迹的方程呢？

意图：让学生独立获取轨迹的方程，体会建立直角坐标系的方法，并由得到的方程认识轨迹.

师生互动：（1）让学生根据自己的经验建立坐标系，并求出相应的方程.

（2）教师展示几个有代表性的建系方法及所求出的方程，引导学生进行观察分析，发现方程是不同于椭圆或双曲线的方程的，所以问题1中的曲线既不是椭圆的一部分，也不是双曲线的一支，它是另外一种曲线.

［问题4］ 你会怎样给上面的轨迹下定义？它的标准方程是怎样的？

意图：获得抛物线的定义，形成抛物线的概念.

师生互动：（1）请学生表述抛物线的定义，教师在学生的表达基础上进行归纳总结.

（2）分析学生在问题3中得出的方程，找出最简单的方程，分析其特点，并由此得出抛物线的标准方程.

（3）同学交流合作，将四种形式的标准方程及对应的焦点坐标、准线方程写出来.让学生同桌互相检查，得出正确的结果.

（4）让学生观察抛物线四种形式的标准方程，获取它们的共同点和不同点.

（5）提问学生：你能说明二次函数y=ax2（a≠0）的图象为什么是抛物线吗？请指出它的焦点坐标、准线方程.

［问题5］ 请完成下列问题：

（1）已知抛物线的标准方程是y2=6x，求它的焦点坐标和准线方程.

（2）已知抛物线的焦点是F（0，-2），求它的标准方程.

意图：使学生体会抛物线标准方程的应用.

［问题6］ 你能由上面的研究过程总结一下我们是如何研究点的轨迹的吗？

意图：进行本节课的小结，提出进一步研究的问题.师生活动：

（1）教师让学生思考，可以视情况让学生适当地表述自己的想法。

（2）教师提出：本节课我们是如何验证自己的猜想的？

帮助学生认识到：本节课不仅学习了抛物线的知识，更重要的是又一次体会了利用方程研究曲线的坐标法思想.

（3）让学生回顾自己获取抛物线方程的过程，体会不同坐标系下方程形式的不同，并由此认识并掌握建立直角坐标系的一般原则.

（4）回到最初的情境：边长为L的正方形ABCD内，到中心O的距离小于到边的距离的点所组成的图形记为S，S的边界是什么曲线？有兴趣的同学回去可以研究一下图形S的面积，对于这样一类新的图形面积是否需要探求新的求解方法.

六、目标检测设计

（1）73页，A组第1题、第4题.

意图：巩固落实今天的基础知识，掌握抛物线的概念和标准方程.

（2）74页，B组第3题.

意图：使学生体会“坐标法”的应用.

（3）姚明有一次投篮时，测得投篮的轨迹是抛物线，已知抛物线最高点离地面距离为4米，篮筐高为3米，篮筐中心距离最高点的水平距离为2米.请你建立适当的坐标系，求抛物线的标准方程和焦点坐标.要想计算出姚明与篮筐中心的水平距离，你还需要知道什么条件？