例谈消元法在初中数学解题中的应用

方逵香

（山东省莱芜市莱城区花园学校，山东 莱芜）

初识消元法，好多学生狭隘地以为消元法只是应用于解方程组，事实上消元是一种简化运算的重要思想，它在初中数学题中有着广泛的应用。本文通过鲁教版七年级下册中的部分题目，对消元法在初中数学解题中的应用作介绍，以供参考，希望能起到抛砖引玉的作用。

例1.解下列方程组

仔细观察方程组（1），属于比较对称的一种，可以把分母为6的部分及分母为7的部分都各自视为一个整体，如分别设为m，n。采用整体换元的方法得到然后再化简得到关于x，y的方程组，从而解得x，y的值。本题在解方程组的过程中，巧妙进行了换元，将方程组化繁为简，从形式和计算上都大大简化，降低了解题难度。这种整体换元的方法也是一种消元思想，它的妙处不言而喻。

方程组（2）也是由比较特殊的对称方程组成的，题目比较简单，学生解题时多数是采用了代入消元法，但是有的同学代来代去容易晕头转向而弄错。针对题目特点，采用加减消元法，问题就相当容易处理。具体解的过程是：

①+②+③合并化简得：

x+y+z=20④

④-①得z=5

④-②得x=15

④-③得y=0

选对了方法后整个求解的过程变得简单轻松，视觉上也对仗整齐，利落美观。

例 2.若 4x+3y+5=0，则 3（8y-x）-5（x+6y-2）的值等于 _____。

分析：本题中有两个未知数，条件中却只有一个方程，无法直接求得x，y的具体值，根据经验必定有特殊解法。故而先将要求的代数式进行化简。

原式=-8x-6y+10，对照已知条件，移项得4x+3y=-5，然后将其整体代入原式，消去两个未知数，从而求得结果。本题通过整体代入消元，将未知数消灭的无影无踪，消元的威力可谓大矣。

分析：本题给定了两个方程，却有3个未知数。如上题一样，不能采用常规方法解方程组。观察题目，发现两个方程右边n的系数相等，符合加减消元的特点，不妨欲扬先抑，先消去n再说。

故而，②-①得：x+2y=2 ③，结合已知中另一条件得到x+y=12 ④，将③④联立可求得x，y的值，再代入①，即可求得n值。这样做似乎已经很简单了，但是，如果继续采用加减消元的思想，将 ③+④得：2x+3y=14。蓦然回首已知中的方程①，惊喜地发现n值已经跃然纸上。消元法再次给了我们一个惊喜！消元法不仅在解方程组、求值等代数运算中，起着化繁为简，拨云见日的作用，在几何题中也有着广泛的应用。

例4.△ABC和△A1B1C1中，∠A，∠B，∠C所对的边分别是a，b，c，∠A1，∠B1，∠C1所对的边分别是 a1，,b1，c1，∠A+∠B=∠C，∠B1+∠C1=∠A1，且 b-a=b1-c1，b+a=b1+c1，则这两个三角形是否全等？若全等，请给出证明；若不全等，请说明理由。

分析：要想证明是否全等，必须知道对应边和对应角的关系，题目中只有边角的和差关系，并没有单个边或角的关系。故而要经过计算整理得到单个角或边的关系。面对四个等式不少学生一筹莫展，可是只要借助代数的方法，巧用消元即可迎刃而解。

解：∵∠A+∠B=∠C，∠B1+∠C1=∠A1

又∠A+∠B+∠C=180°，∠A1+∠B1+∠C1=180°

∴2∠C=180° 2∠A1=180°（代入消元）

∴∠C=∠A1=90°

∵

①+②得：b=b1（加减消元）

将b=b1代入②得a=c1（代入消元）

∴△ABC≅△A1B1C1（SAS）

例5.已知：如图，AM、CM分别平分∠BAD和∠BCD。

求证：（1）如果∠B=32°，∠D=38°，求∠M的度数；（2）∠M=1/2（∠B+∠D）。

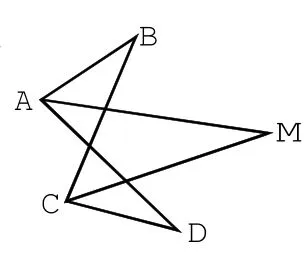
分析：不少学生只能通过三角形的内角和或外角定理求得第一问。对于第二问有的不知从哪里下手，有的求证过程相当麻烦，最后无疾而终。如果运用方程思想，列出方程，再借助代入消元和加减消元法，问题就大大简化。如此一来，得到关于求∠M的算式，回过头由一般到特殊，将第一问中的已知条件代入算式验证，或者先做第二问就更简单了，可谓一举两得。

证明：∵AM、CM平分∠BAD和∠BCD

∴∠BAM=∠DAM=1/2∠BAD=m ①

∠BCM=∠DCM=1/2∠BCD=n ②

∵∠B+∠BAM=∠M+∠BCM

∠D+∠DCM=∠M+∠DAM

将①②中相应的值代入上两式得：

∠B+m=∠M+n ③

∠D+n=∠M+m ④

③+④得：

2∠M=（∠B+∠D）

∴∠M=1/2（∠B+∠D）。

数学学习中有许多先进的思维方式，比如方程思想，消元思想等等，培养学生运用这些思维方式，训练学生抓住问题本质的能力，有利于快速准确地解决数学问题，提升学生的学习兴趣和自信心。作为数学教师，引领学生的思维是我们的责任。