A Risk-averse Two-Stage Stochastic Optimization Model for Water Resources Allocation under Uncertainty
Ye Xu, Sha Li, Feng Liu, Jinping Qian, Yanpeng Cai, Guanhui Cheng
1 MOE Key Laboratory of Regional Energy and Environmental Systems Optimization, College of Environmental Science and Engineering, North China Electric Power University, Beijing 102206, China
2 School of Materials and Metallurgy, University of Science and Technology Liaoning, Anshan 114051, China
3 College of Resources and Environmental Sciences, Hebei Normal University, No.20 Road East. 2nd Ring South,Yuhua District, Shijiazhuang, Hebei, 050024 China
4 State Key Laboratory of Water Environment Simulation, School of Environment, Beijing Normal University, Beijing 100875, China
5 Faculty of Engineering, University of Regina, Regina, Saskatchewan, Canada S4S 0A2
1 Introduction
Over past few decades, water shortage crisis always has been a puzzle for governmental authorities, research institutions and local management departments around the world. The water resource amount of per capita in China is almost 2220 m3, which accounts for about a quarter of the average level worldwide. It is predicted that total population in China will reach 1.6 billion and available water amount of per capita will drop by 1760 m3, which is closing to regulated standard (1700 m3) of water-deficient nations. A group of numbers could better reflect the water shortage situation in China. The drought area is probably 5 million km2and reaches 52 percent of total land area. The number of water-poor cities could be over 400 and nearly twothirds of total amounts. The economical loss caused by water shortage is approximately 200 billion RMB per year (Song et al., 2005; Feng et al., 2014). In addition, the controversies and conflicts in water allocation among municipal, industrial and agricultural users are intensified. This fact might trigger the social instability.Therefore, the issue about how to overcome water crisis becomes more and more critical, because it relates not only to social and economic development, but also to national security.
To tackle the problem mentioned above, some engineering measures are utilized, including water resource protection, intermediate water reuse and inter-basin water transfers project. Although these activities have alleviated the water scarcity relatively; however, over-high costs and intrinsic technological limitations associated with these projects affected their further applications. The decision makers are thus interested in exploiting some system analysis approaches for designing and generating rational water allocation patterns,which are useful supplements to engineering measures. Nevertheless, the water resource management system is complicated with multi-level system structure and multi-type system components. For example, at least three levels are included in this system, such as decision-making level, water-project level and user level. The system elements mainly include natural, social-economic and engineering factors. Moreover, many factors may exhibit intrinsic and inherent uncertainties, resulting in the difficulties in generating effective management schemes. It is thus desired that an effective uncertain optimization model is developed.
Previously, a significant amount of uncertain optimization approaches were developed for dealing with the water resources management problems, which mainly include stochastic mathematical programming (SMP),fuzzy mathematical programming (FMP) and interval mathematical programming (IMP) (Wagner et al., 1994;Huang, 1996; Wilchfort and Lund, 1997; Jenkins and Lund, 2000; Maqsood et al., 2005; Jia and Culver, 2006;Li and Huang, 2007; Liu et al., 2007; Qin et al., 2007; Han et al., 2008; Fattahi and Fayyaz, 2010; Xu et al.,2009, 2012, 2014, 2017; Li and Zhang, 2015; Li et al., 2015; Xu and Huang, 2016; Liu et al., 2017). Among these techniques, the two-stage stochastic programming (TSP) model was applied in water allocation fields extensively (Huang and Loucks, 2000; Li and Huang, 2007; Xu et al., 2009; Xu and Huang, 2016). This is mainly due to the facts that (i) the uncertain factors related to water management system present as the random properties, such as available water amounts; (ii) the policy makers involving some large projects should firstly know the water amount supplied to them in a long-term planning horizon in order to identify an initial production scale and then determine appropriate decisions based on explicit water amount information. The main advantages of TSP model are that it can effectively tackle probabilistic distribution information and design corrective actions after a random event has taken place, leading to rational management strategies (Birge and Louveaux, 1988). Nevertheless, TSP model also has an obvious drawback in model structure and may lead to suboptimal solutions. In detail, the TSP model selects the expected value calculated through various probabilistic scenarios as the objective function and without considering potential risk of model instability. In fact, the minimization (or maximization) of expected objective value is realized at the expense of objective value under some specific scenarios, which is incapable of ensuring the objective value under each scenario is minimized or maximized, incurring the low system stability. Moreover, this drawback will be further magnified under uncertain condition. The necessary improvement in the objective function will enhance the applicability and feasibility of TSP model.
Therefore, as the first attempt in the related field, this study aims to develop a risk-averse two-stage stochastic programming (RATSP) model for dealing with the water resources management issue. The RATSP model effectively ensures the optimality of the objective value under various scenarios through incorporating the financial risk into the objective function. A variety of solutions are obtained through adjusting the weight coefficients and targeted values of system benefit, which are suitable in evaluating the trade-off between system economy and reliability. The proposed RATSP model will be applied to a case study involving the water resources allocation problem among various users. The paper will be organized as follows. The formulation and solution processes of RATSP model will be introduced in “Methodology” section; meanwhile, a specific RATSP model for water resources allocation is formulated in this section. The “Case study” section will mainly describe a hypothetical water resources management system. The “Result analysis” section will analyze the variation trends of the solutions generated from RATSP model and provide the improvement of the RATSP model in the future. The summary will be provided in the “Conclusion” section.
2 Methodology
Considering a water resource management system, where main system components are affected by many factors and are associated with the random uncertainties. For example, available water quantity is mainly depending on climatic and meteorological conditions, hydrological situation, water infrastructure and water transportation network. It may exhibit random characteristic and is thus assumed as random variables based on long-term observation data. In addition, promised water quantity is extremely important to users, since the design and generation of investment alternatives are mainly affected by how much water they can expect(Huang and Loucks, 2000; Xu et al., 2009). The water users (including the industrial, agricultural and municipal sections) normally will not make a major investment in irrigation infrastructure and water intensive projects, while they know there is only a small chance of receiving sufficient water. Conversely, while these consumers estimate received water amount in the future is sufficient, they will make a major investment for realizing rapid economic development. Therefore, the manager should give a quantity of water that is promised to various users; meanwhile, the information about how much water can be allocated is as accurate as possible.Moreover, based on predefined allocation target, the manager should ensure that available water is allocated with the minimization of any associated penalties or negative consequences, where associated penalties mean the water acquisition from higher-priced alternatives, and negative consequences are sourced from the curbing of the development plans (Howe et al., 2003; Li and Zhang, 2015; Liu et al., 2017). To tackle above problems, the TSP model will be appropriate.
Within a TSP framework of water allocation system, the meaning of “two stage” is that a decision of water allocation target needs to be made at the first stage before the available water amounts are known; a recourse action can then be taken at the second stage, when uncertainties of water quantity are identified and the allocated targets are determined. The objective of TSP model is designed as the maximization of net system benefit, which is expressed as the difference between the profits generated from water allocated to various consumers and the cost caused by promised water cannot be delivered; the constraints mainly included the water requirements of various users, the limitation of available water amounts and some non-negativity regulations.A TSP model for water allocation problem could be formulated as follows (Huang and Loucks, 2000; Xu et al., 2009):
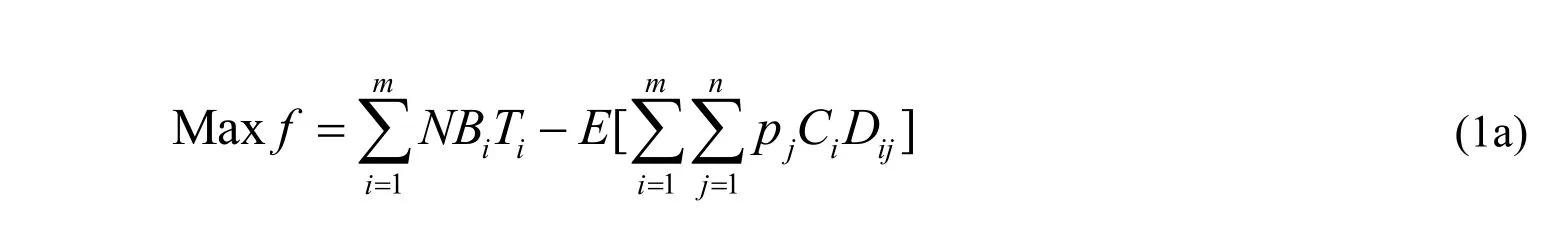
Subject to:
垫片式转轮静平衡试验工具的优点是省去了丝杠,克服了梯形螺纹间螺距大、加工螺纹与丝杠中心线不垂直的缺点;同时平衡球直接使用轴承球,球的形状、表面粗糙度、硬度均好于自己加工的平衡球,克服了平衡球加工到最高点时线速度为零的缺点。
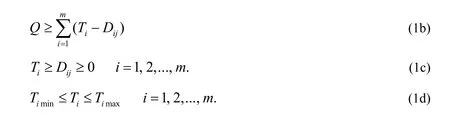
wherefis the net system benefit;NBiis the profits generated from useriwhen per unit of water is delivered;Tiis designed water allocation target at the first stage that is promised to useri;E[⋅] is calculated expected value under various scenarios;Ciis penalty cost to useriwhen the water requirement is not satisfied(Ci>NBi);Qis total available water amount, which is expressed as the fixed values (qj) under various probabilistic scenarios (pj) forj=1,2,… ,n;Dijis the deficit amount by which water allocation targetTiis not met;TiminandTimaxis the minimum and maximum allowable allocation amount for useri;iis the type of water users;mis the number of water users;jis the probability type of the occurrence in various streamflow levels (Huang and Loucks, 2000; Xu et al., 2009).
As described in the “Introduction” section, the maximization of expected objective value is incapable of realizing the maximization of the objective value under each scenario. Therefore, the financial risk associated with the water resources allocation should be incorporated into the TSP framework, which could ensure the objective value under various scenarios will reach predetermined target level as possible. Referring to Barbaro and Bagajewicz (2004), the financial risk can be defined as the probability of not meeting a predetermined profit level referred to as Ω. For a model (1), the financial risk associated with the decision variablesTand a target profit Ω is expressed as following probabilistic form (Barbaro and Bagajewicz, 2004) :
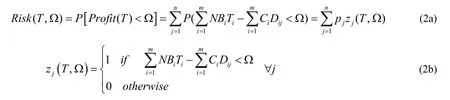
where the equation (2b) means that designed parameter value (zj) is either zero or one according to the comparison results between system benefit under each scenario and target benefit. In detail, for any scenario, the profit is either greater or equal than the target level, in which case the respective probabilityis zero, or the profit under specific scenario is smaller than the target, leading to a probability of one. Therefore, model (1) can be reformulated through incorporating two equations (2a) and (2b) into the objective function and constraints, where a risk-averse two-stage stochastic programming model (RATSP)is written as follows:
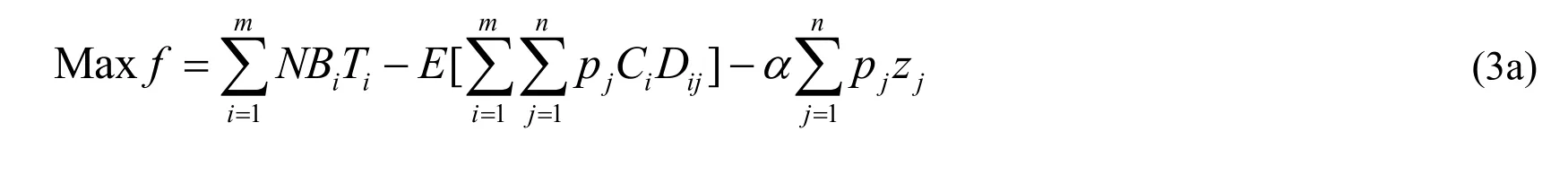
Subject to:
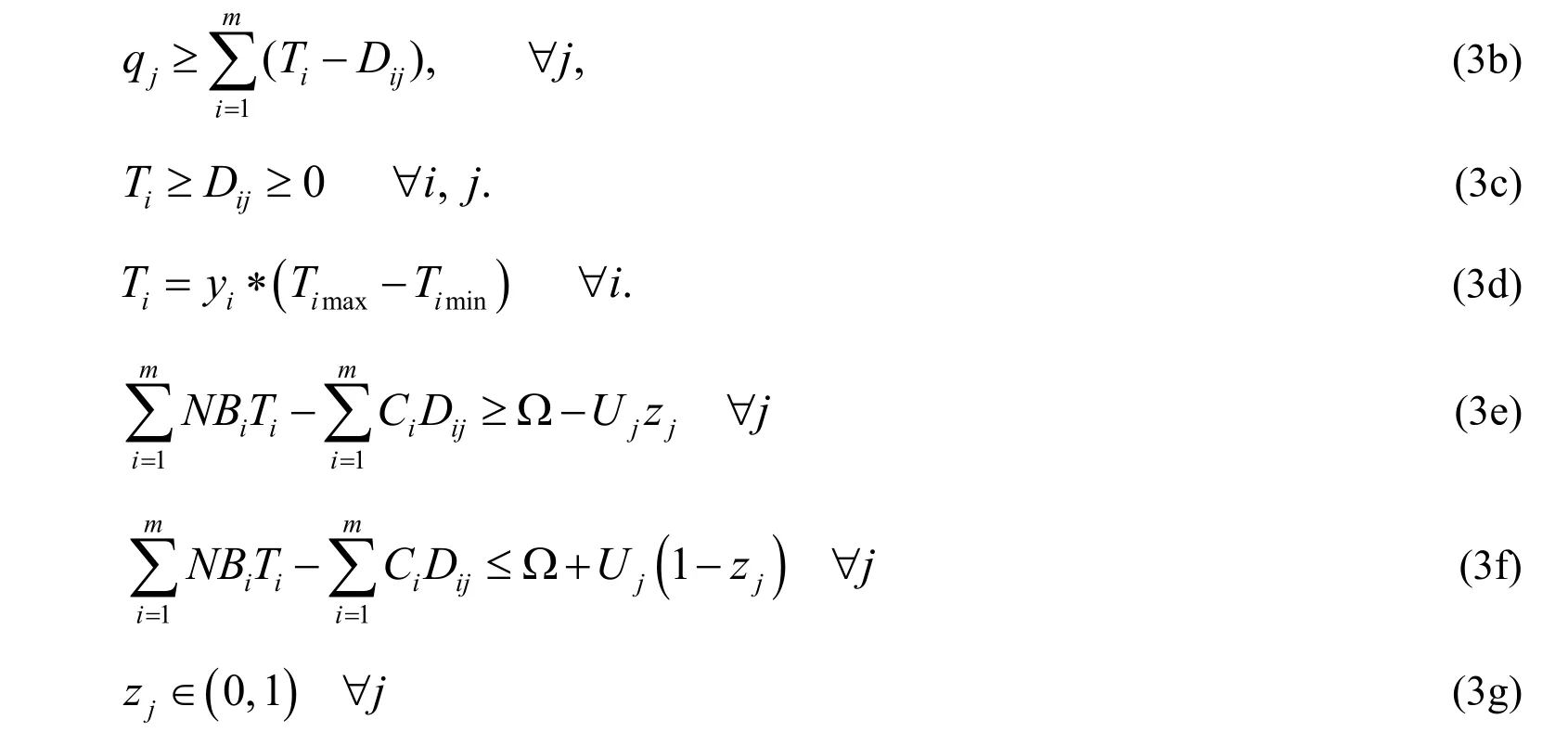
where the constraint (3d) is used to calculate the allocation targetTithrough introducing the intermediate decision variableyi. The constraints (3e) and (3f) are used to ensure new integer variablezjis zero when the profit for scenariojis greater than or equal to the target level Ω and a value of one otherwise. To do this, potential high benefit under each scenario (Uj) is used. The binary variables (zj) represent the penalty caused by possible financial risk; meanwhile, the weight coefficientαis used to reflect relative importance of financial risk compared with the net system benefit. Finally, optimal allocated target (Ti), deficit amount (Dij) and net benefit (f) are obtained through solving model (3). Therefore, optimal water allocation scheme is determined as follows:
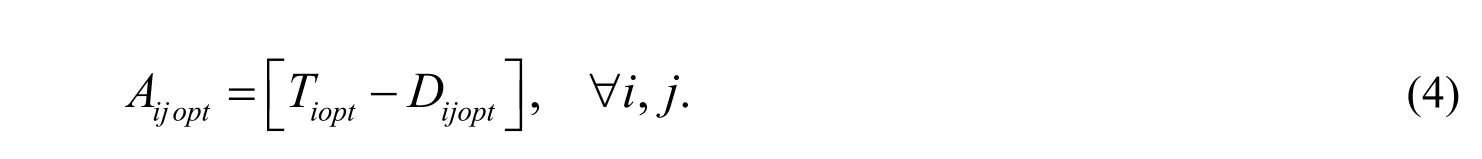
Figure 1 shows the formulation and solution processes of proposed RATSP model, where RATSP model is developed through incorporating the financial risk measure into original TSP framework. This innovative combination is capable of avoiding potential financial risk and generating stable and reliable solutions under each scenario, which are beneficial for local managers. The detailed procedures of formulating and solving this model are summarized as follows:
Step 1: Identify uncertain variables and acquire related probabilistic distribution and risk magnitude information (e.g., available water amounts, the limitations in allocated amounts, the benefit of production activities and possible penalty, predetermined profit target).
Step 2: Formulate a traditional TSP model based on system investigation and analysis.
Step 3: Reformulate a RATSP model through introducing the financial risk measure.
Step 4: Transform the RATSP model into general deterministic model through defining the target level (Ω)and potential high benefit (Uj).
Step 5: Generate the model solutions, including allocated water target (Ti), deficit amount (Dij), net benefit (f)
and water supply amounts (Aij), respectively.

Table 1 The system parameters presented as the deterministic values
3 Case Study
A designed hypothetical case of the water resources management system will be used to demonstrate the feasibility and applicability of proposed RATSP model (As shown in Figure 2). Within this water supply management system, optimal water supply amounts from water sources to users are determined by local manager in order to realize the maximization of total system benefit, where the users are divided into three types, i.e.an industrial, municipal and agricultural user. The system revenue will be generated when required water amounts of each user are satisfied; conversely, if promised water is not delivered, the economic loss caused by the high purchase cost or impaired production activities is unavoidable. Many types of system parameters are involved in this decision process, including water amounts delivered from the water sources, the limitations in the water amounts allocated to various users, the economic revenue generated by the water utilization of each user and the penalty caused by deficit amounts. Among them, some parameters exhibit uncertain characteristics due to their inherent and intrinsic statistical features or estimated errors. For example, available water amounts are mainly depending on long-term streamflow prediction and are thus assumed as discrete random variables, where they are expressed as fixed values under various scenarios, being 4.5, 12 and 19 m3under three probabilistic levels of 0.2, 0.6 and 0.2, respectively. Other parameters, such as the minimum and maximum allocation target and economic parameters, are suitably expressed as the deterministic values due to their complete historical records and small variation ranges. Table 1 provided the parameters information.TSP model is suitable in executing the recourse actions and dealing with random uncertainties mentioned above.

Fig. 1 The formulation and solution framework of proposed RATSP model
In fact, as described in above two sections, the maximization of expected system benefit is incapable of ensuring optimal system performance under each designed scenario. The introduction of financial risk measure could guarantee that the system revenue under each scenario is closing even reaching predetermined target level, such that system feasibility and stability were enhanced. In this management system, predefined target level (i.e. Ω) is designed and determined based on the calculations and estimations in net system income. Finally, three situations are selected (i.e. the low, medium and high income) and each situation includes four fixed target values, where the values under the low condition are 225, 250, 275 and 300 $, respectively; those under the medium condition are 600, 625, 650 and 675 $, respectively; those under the high condition are 650, 675, 700 and 725 $, respectively. As for potential high benefit under various scenarios (Uj),three groups of parameters are assumed for matching the target level, being 400, 425 and 500 $, 700, 750 and 800 $, 1000, 1100, 1200 $, respectively. Therefore, the problem under consideration is how to generate the maximum system benefit under random uncertainties and ensure the system stability as possible. To solve this problem, the proposed RASRP model is considered to be suitable.
4 Results Analysis
Table 2 shows generated part of solutions of RATSP model under various combinations of the weight coefficients (α) and target level (Ω). After a series of tests, the coefficientsα= 1 andα= 1000 are selected as the representatives. As shown in Table 2, the variations in the target benefit would lead to various allocation patterns when weight coefficient remains unchanged. For example, at a coefficient ofα= 1000, as the increases in target value, the water amounts delivered to agricultural user would increase; meanwhile, water amounts allocated to other two users were unchanged. For example, under the medium target value, received amounts of agricultural user at three streamflow levels are 0, 5.5 and 5.63 m3, respectively; the delivered amounts un-der the high condition were 0, 5.5 and 6.41 m3, respectively. The reason causing such a variation is that the increases in Ω value lead to strict requirement in economic performance of this water management system.The increase in utilized water amounts is capable of realizing the maximum economic revenue and avoiding the financial risk. Similar situation also occurs under another weight coefficient (i.e.α= 1), where total water amounts allocated to municipal user were increased, being 7.4 and 7.5 m3under the low and medium values,respectively.
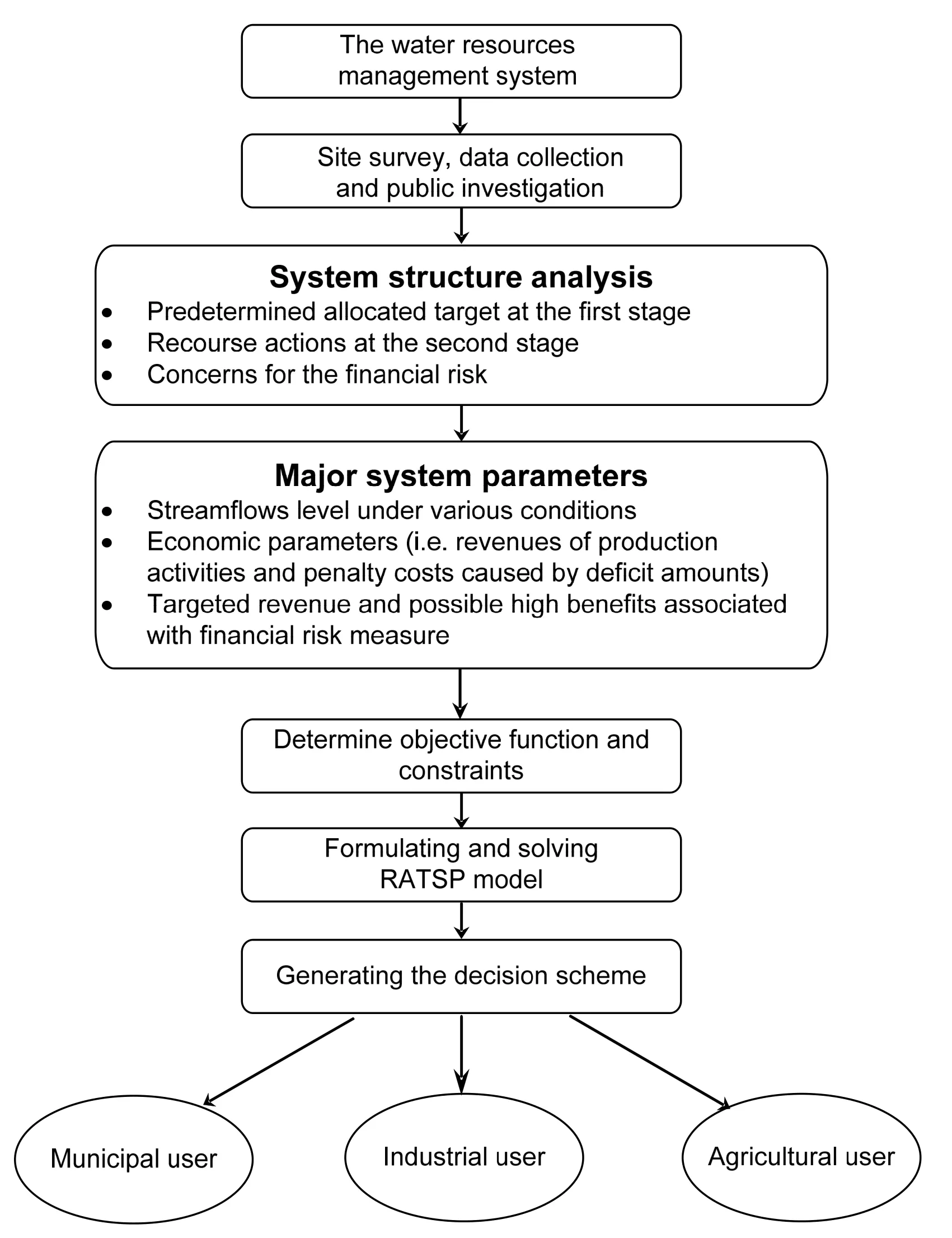
Fig. 2 The schematic map of this water resource management system

Table 2 Solutions of the RATSP model under various conditions
The weight coefficients also exert the influence on generated decision variables. For example, as the increase of weight coefficient, total amounts allocated to agricultural user under the medium and high values were increased, while the water amounts delivered to other two users were stable. As demonstrated in Table 2,as the increase in the weight coefficient, total water utilized amounts of agricultural user under the medium condition are 11 and 11.13 m3, respectively; those under the high condition are 11 and 11.91 m3, respectively.This is due to the fact that the increase in weight coefficient means that the financial risk obtained more concerns, such that the decision schemes with the high revenues are more popular. The increase in delivered water amounts is in favor of production activities of the users, leading to possible high revenues of entire system.
In fact, other parameters also affect the model results, including economic parameters and streamflow level. Firstly, the revenues and penalty costs related to three users exert direct influences on generated decision patterns. The incomes and costs of agricultural user are lower than those of municipal and industrial users.Therefore, its water requirement has not been met, leading to the largest deficit amounts. For example, at a coefficient ofα= 1, total deficit amounts of three users (i.e. municipal, industrial and agricultural users) under the low condition are 0.1, 2 and 3.56 m3, respectively. Those under the medium condition are 0, 2 and 5.5 m3,respectively. This is because the water requirement of municipal user with the high income and penalty cost should be satisfied in priority in order to generate the maximum system benefit. Unavoidably, the interest of agricultural user with the low revenue and penalty cost will be impaired. Moreover, the runoff volume also has the influence on water allocation pattern, since it is associated with water supply amounts. As shown in Table 2, the deficit amounts would appear mostly under the low streamflow level and occasionally under the medium level. For example, underα= 1 and the low target value, total deficit amounts of three users under three streamflow levels were 7.56, 0.10 and 0 m3, respectively; those under the medium target value were 7.5,0 and 0 m3, respectively. This also reflects the importance in parameters survey and identification, since they play a critical role in model formulation and solution processes.

Fig. 3 Net benefits generated from RATSP model under different conditions
The variations in system parameters not only exert the influence on decision variables, but also on the objective values. In order to better reflect the influence of financial risk concern on the objective values, the system revenues at each streamflow level and their expected values are calculated separately, which are shown in Figure 3. As shown in Figure 3, as the increase in the streamflow level, total system income would increase.For example, underα= 1 and the low target value, the system benefit under three streamflow levels are 593.22, 659.11 and 672.78 $, respectively; similarly, underα= 1000 and the medium target value, those are 594.75, 671.25 and 675.00 $, respectively. This is mainly due to the fact that the production revenue of three users are related to their utilized amounts, where their change trends are consistent. Moreover, the increase in target value also leads to the increase in the system revenues at each streamflow level. For example, the system incomes underα= 1000 and the low target value are 562.67, 594.75 and 611.94 $, respectively; those under the medium level are 628.33, 671.25 and 672.81 $, respectively; those under the high level are 628.33,675.00 and 700.00 $, respectively. This is because the increase in target value required a satisfactory economic performance of entire system; otherwise, the financial risk would appear. Finally, the objective values would change as the change in the weight coefficient, where its increase would lead to the increase in system benefits under each streamflow level. For example, the incomes under the low streamflow level and medium target value are 592.00 and 594.75 $, respectively; those under the low streamflow level and high target value are 592.00 and 611.94 $, respectively. This variation also reflect the significance of the risk analysis, where it could effectively ensure the system economy under each streamflow level, such that the system stability was enhanced. However, the expected objective values would decrease as the increase in the weight coefficients,being 592 and 584.75$ under the high target, respectively. This also reflected the trade-off between system economy and stability, where the increase in expected value is realized through reducing the revenue under specific scenario. In fact, the economic-effective allocation pattern with balanced feature is favorite for decision maker, where the solution underα= 1000 and the medium target value is recommended as the decision basis.
The above results demonstrate that RATSP model owns the advantages in following three aspects: (i) it addresses the uncertain parameters as the fixed values under various scenarios and provide a linkage between predetermined allocated range and associated economic performance; (ii) it incorporates the financial risk measure into the objective function and analyzes the trade-off between system economy and stability; (iii) it generates a variety of solutions under different combinations of system parameters which can provide more decision spaces and rational decision basis to local managers. However, it still needs to be improved in some aspects. Firstly, various target values are designed for calculating the financial risks. As demonstrated in the"Result analysis" section, the determination of the target value is directly associated with generated solutions.Therefore, how to determine a set of comprehensive and rational target values is very critical for generating effective decision patterns. Secondly, a variety of solutions are obtained through adjusting the target level and weight coefficient, which enrich the decision space. Nevertheless, it also leads to the complexities and difficulties in selecting an appropriate solution as decision basis. Therefore, the selection of suitable evaluation criteria and methods will be critical. Finally, as two important branches of uncertain optimization methods,fuzzy and interval programming approaches should be incorporated into RATSP model for tackling complex management issues.
5 Conclusion
In this study, a risk-averse two-stage stochastic programming (RATSP) model was developed for tackling the water resource allocation problem. Compared with traditional TSP models, the significant contribution made by RATSP model was that it emphasized the importance of financial risk caused by the low system benefit under specific scenario and avoided the solutions deviation sourced from traditional expected objective function.
The applied results of RATSP model in a water management system demonstrated that a variety of water allocation alternatives are obtained through adjusting the target level and weight coefficient, which provided more decision space to local managers. Among them, the scheme realizing the balance between system economy and stability is recommended as the decision basis. In the future, some meaningful improvements, including accurate identifications and estimations in some critical parameters, the incorporation of multi-criteria decision analysis techniques and uncertain optimization approaches, are deserved to be further studied for handling complex management issues.
Acknowledgements
This research was supported by the Natural Sciences Foundation of China (71303017), National Key Research and Development Plan (2016YFE0102400) and Fundamental Research Funds for the Central Universities (2017MS050).
Barbaro, A. and Bagajewicz, M.J. (2004), Managing financial risk in planning under uncertainty,Process Systems Engineering50,963-989.
Birge, J.R. and Louveaux, F.V. (1988), A multicut algorithm for two-stage stochastic linear programs,European Journal of Operational Research34, 384-392.
Fattahi, P. and Fayyaz, S. (2010), A compromise programming model to integrated urban water management,Water Resource Management24, 1211-1227.
Feng, Z.M., Yang, Y.Z. and You, Z. (2014), Research on the water resources restriction on population distribution in China,Journal of Natural Resources29(10), 1637-1648. (In Chinese)
Han, Y., Xu, S.G. and Xu, X.Z. (2008), Modeling multisource multiuser water resources allocation,Water Resource Management22,911-923.
Howe, B., Maier, D. and Baptista, A. (2003), A language for spatial data manipulation,Journal of Environmental Informatics2, 23-37.
Huang, G.H. (1996), IPWM: An interval-parameter water quality management model,Engineering Optimization26, 79-103.
Huang, G.H. and Loucks, D.P. (2000), An inexact two-stage stochastic programming model for water resources management under uncertainty,Civil Engineering and Environmental Systems17, 95-118.
Jenkins, M.W. and Lund, J.R. (2000), Integrating yield and shortage management under multiple uncertainties,Journal of Water Resources Planning and Management126(5), 288-297.
Jia, Y. and Culver, T.B. (2006), Robust optimization for total maximum daily load allocations,Water Resources Research42,W02412.
Li, C.Y. and Zhang, L. (2015), An inexact two-stage allocation model for water resources management under uncertainty,Water Resources Management29(6), 1823-1841.
Li, W., Liu, M., Wu, S.Z. and Xu, Y. (2015), An inexact optimization model associated with two robust programming approaches for water resources management,International Journal of Environmental Science and Technology12(7), 2401-2414.
Li, Y.P. and Huang, G.H. (2007), Inexact multistage stochastic quadratic programming method for planning water resources systems under uncertainty,Environmental Engineering Science24(10), 1361-1377.
Liu D., Liu, W.T., Fu, Q., Zhang, Y.J., Li, T.Q., Imran, K.M. and Abrar, F.M. (2017), Two-stage multi-water sources allocation model in regional water resources management under uncertainty,Water Resources Management, 31(2), 1-19.
Liu, Y., Guo, H.C., Zhou, F. and Qin, X.S. (2007), An inexact chance-constrained linear programming model for optimal water pollution management at the watershed scale,Journal of Water Resources Planning and Management (ASCE)134, 347-356.
Maqsood, I., Huang, G.H. and Yeomans, J.S. (2005), An interval-parameter fuzzy two-stage stochastic program for water resources management under uncertainty,European Journal of Operational Research167, 208-225.
Qin, X.S., Huang, G.H., Zeng, G.M., Chakma, A. and Huang, Y.F. (2007), An interval-parameter fuzzy nonlinear optimization model for stream water quality management under uncertainty,European Journal of Operational Research180(3), 1331-1357.
Song, X.S., Shi, P.J. and Jin, R. (2005), Analysis on the contradiction between supply and demand of water resources in China owing to uneven regional distribution,Arid Zone Research22(2), 163-166. (In Chinese)
Wagner, J.M., Shamir, U. and Marks, D.H. (1994), Containing groundwater contamination: Planning models using stochastic programming with recourse,European Journal of Operational Research7, 1-26.
Wilchfort, O. and Lund, J.R. (1997), Shortage management modeling for urban water supply systems,Journal of Water Resources Planning and Management123(4), 250-258.
Xu, Y., Huang, G.H. and Qin, X.S. (2009), An inexact two-stage stochastic robust optimization model for water resources management under uncertainty,Environmental Engineering Science26, 1765-1776.
Xu, Y., Huang, G.H. and Xu, T.Y. (2012), Inexact management modeling for urban water Supply systems,Journal of Environmental Informatics20(1), 34-43.
Xu, Y. and Huang, G.H. (2016), A risk-based interval two-Stage programming model for agricultural system management under uncertainty,Mathematical Problems in Engineering7438913.
Xu, Y., Li, W. and Ding, X.W. (2017), A stochastic multi-objective chance-constrained programming model for water supply management in Xiaoqing river watershed,Water14(2), 171-183.
 Journal of Environmental Accounting and Management2018年1期
Journal of Environmental Accounting and Management2018年1期
- Journal of Environmental Accounting and Management的其它文章
- The Relationship Between Environment Operational Performance and Environmental Disclosure of Nigerian Listed Companies
- The Relationships Between Contextual Variables and Perceived Importance and Benefits of Environmental Management Accounting (EMA) Techniques
- Analyzing Structure and Driving Force of Steel Consumption in China
- Ecological Interstate Systems as an Object of Legal Research
- Examining the Effect of Emotion to the Online Shopping Stores’ Service Recovery: A Meta-Analysis
- Disclosure of Environmental Matters – Galp Energy
