任意平面阵干涉仪二维测向方法*

张 敏，刘金彦，郭福成

(1.国防科技大学电子科学学院，湖南 长沙 410073； 2.武警警官学院，四川 成都 610200)

0 引言

估计信号来波方向(AOA)，又称之为测向，在电子侦察、监视、预警、通信等领域受到广泛关注和研究[1-4]。其中基于相位干涉仪的测向技术，由于其原理简单、测向精度高，应用越来越广泛[3 ]。当基线长度大于信号半倍波长时，相位差测量可能会出现2π模糊。解相位差的2π模糊是干涉仪测向研究中的主要问题[4]之一。

一种常用的方法是采用长短基线干涉仪形成多基线实现解模糊。如文献[5]基于长短组合基线、文献[6]基于剩余定理互质基线和文献[7]虚拟基线的解模糊方法，但这都要求多组基线之间有一定的几何约束关系，因此限制了干涉仪基线的布阵，且通常仅适用于线阵，较难推广到任意平面阵。

文献[8]的无模糊长基线解模糊方法，仅适用于特定的平面阵型，且该方法中对相位差的多次代数运算造成了较大的测向误差。文献[9]聚类法和文献[10]立体基线解模糊方法通常可适用于任意平面阵，但此类方法仅由特定的几组基线得到多个待定的角度估计，利用剩余基线在此待定角度中选取一个值作为估计值，不能达到测向理论精度。

文献[11]相关干涉仪测向方法可适用于任何阵型干涉仪，且使用了所有基线用于测向，但是基于网格搜索的相关干涉仪测向方法需要将网格划分得足够小，才能得到较好的结果，特别是二维测向条件下，计算量大，实时性差。粒子群优化(PSO)等智能方法虽然运算量有所降低，但由于采用随机搜索策略，在粒子数量较少的情况下，全局寻优能力并不是十分可靠[12]。

文献[13]中的最小二乘(LS)测向适用于任何阵型干涉仪，且使用了所有基线用于测向，但要求相位差无模糊。在主动雷达中，文献[14]中直接利用多个观测站上的干涉仪测量的模糊相位差，对运动目标进行定位跟踪。文献[15]中利用旋转干涉仪模糊相位差直接对固定辐射源定位。这说明直接利用模糊相位差进行测向估计具有可行性。

在此思路下，本文提出了一种多假设非线性最小二乘(Multiple Hypothesis Taylor Series，MHTS)干涉仪测向算法。该算法使用所有基线用于测向，无需事先解相位差模糊，直接利用模糊相位差进行测向，对干涉仪几何构型无特殊要求。

首先给出后文一些数学符号定义：T表示矩阵转置运算，mod表示取模运算，·表示向下取整运算，|·|表示取绝对值运算，‖·‖表示取2范数运算，IN表示N×N维单位矩阵，0N表示N×N维零矩阵。

1 数学模型

1.1 测向模型

本文中方位角α∈[-π,π]定义为入射信号在XOY平面上的投影射线OT′与Y轴正方向的夹角；俯仰角β∈[0,π/2]定义为入射信号与其在XOY平面上的投影射线OT′之间的夹角，如图1所示。

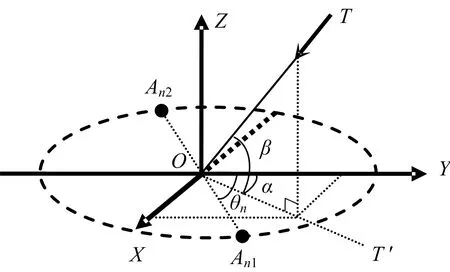
图1 入射角度定义示意图

对应的干涉仪到辐射源的视线矢量为：

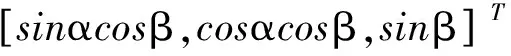
(1)

接收天线An1和An2构成的干涉仪基线n长度为dn，方位安装角为θn，对于二维平面阵，俯仰安装角εn=0，对应的基线指向矢量为：

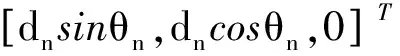
(2)

因此不妨将视线矢量和基线矢量写为：

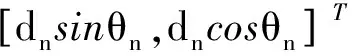
(3)

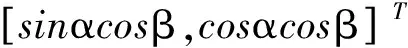
(4)

由此可得干涉仪测量得到的无模糊相位差为：

φn=gnθ+δn，n=1,2,…,N

(5)

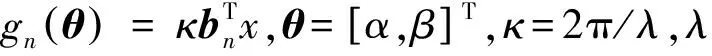
当干涉仪基线长度dn>λ/2时，相位差测量可能会出现2π模糊，因此有：

φn=gnθ+δnmod2π

(6)

式中，φn∈-π,π。

将无模糊相位差写成矩阵形式：

Θ=Gθ+E

(7)

将对应的模糊相位差的矩阵形式为：

Φ=Gθ+Emod2π

(8)

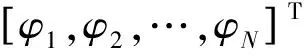
模糊相位差中包含了辐射源角度信息，干涉仪测向问题即是如何利用N组干涉仪基线测量得到模糊相位差，估计出方位和俯仰角。

1.2 相位差噪声模型

多通道干涉仪如图2所示，接收通道对天线接收的信号进行低噪声放大、混频、滤波、A/D等处理，经过FFT等处理得到接收信号到达不同天线的初相位。通过对不同基线的两个天线的初相位相减得到相位差。

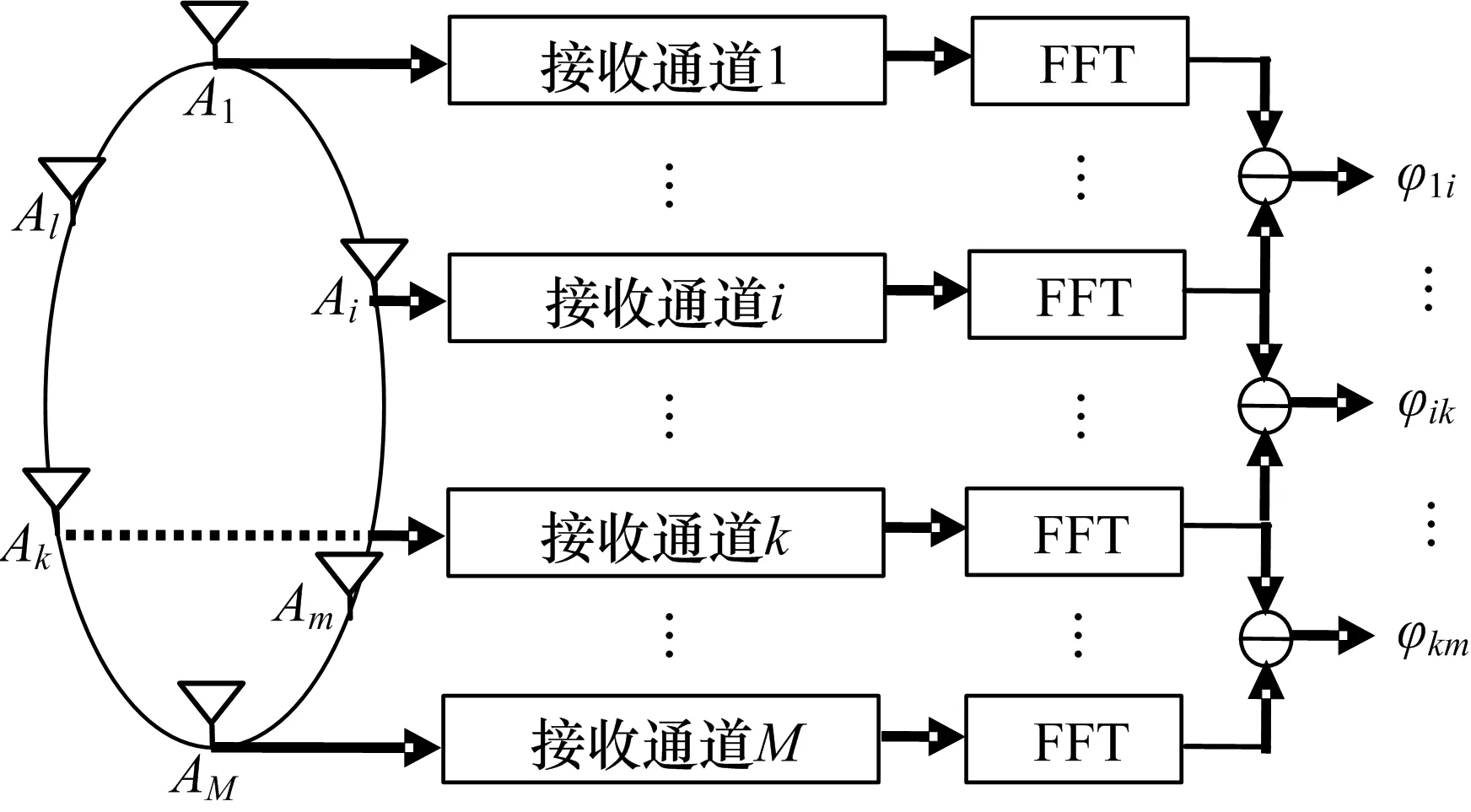
图2 多通道干涉仪示意图

由于各天线和接收通道相互独立，因此接收信号处理后得到的初相位之间可认为近似独立的：

E(ξiξk)=0，i,k=1,2,…,M,i≠k

(9)

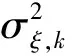
在此条件下，相位差为：

φik=ψi-ψk+δikmod2π

(10)

式中，ψi和ψk为天线i和天线k对应的初相，δik=ξi-ξk对应基线的相位差测量误差。

由此可得相位差噪声特性为：

(11)

式中，l,m=1,2,…,M,l≠m。

本文将此条件下的相位差噪声模型称为相位差的相关噪声模型。

通过机械旋转[16]或电子切换[17]等方式形成时变基线维干涉仪进行测向，通常仅需要2个接收通道，对通道幅/相一致性要求和系统复杂度大为降低。如图3所示的双通道切换干涉仪，在观测时刻tn，通过M选2切换开关，选通2根天线构成干涉仪基线。由于测量的相位差是在不同观测时刻tn，利用不同接收信号在不同基线上得到的，因此测量误差之间可近似看作独立的。在此条件下，相位差为：

φn=ψn1-ψn2+δnmod2π

(12)

式中，ψn1和ψn2为天线1和天线2在观测时刻tn对应的初相，ξn1和ξn2为对应天线初相测量误差，δn=ξn1-ξn2对应基线的相位差测量误差。

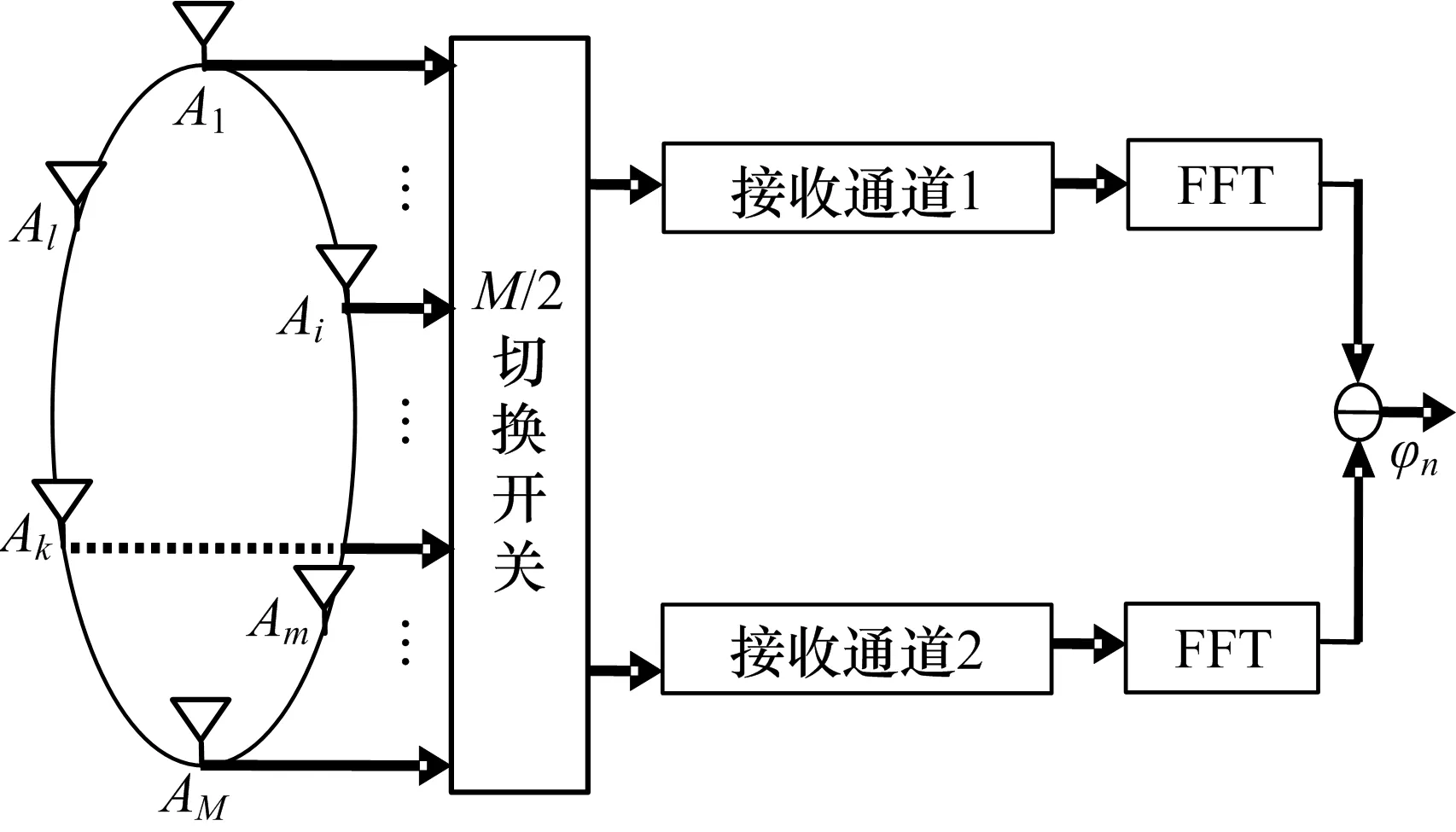
图3 双通道切换干涉仪示意图

由此可得相位差噪声特性为：

(13)

式中，c=1,2,…,N。

本文将此条件下的相位差噪声模型称为相位差的独立噪声模型。

2 测向方法

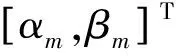
Gθ≈Gθm+Pmθ-θm

(14)

式中，Jacobi矩阵Pm=∂Gθm/∂θm：

Pm=HJm

(15)

式中，H=[κb1,κb2,…,κbN]T，Jm为视线矢量xm关于θm的Jacobi矩阵：

(16)

同时利用初始值得到相位差预测值：

Θm=Gθm

(17)

从而得到相位差测量值和预测值之间的残差：

zm=Φ-Θmmod2π

(18)

利用最小二乘可得：

(19)

需要注意的是，在上述计算中，只有当初值在真值附近时，(18)式中的2π取模运算才能去掉。但由于无法事先获知这一先验信息，受文献[15]中利用干涉仪模糊相位差定位方法的启发，若能在观测空间内选取多个初值，对每个初值采用Taylor级数方法计算，只要有一个初值落在真值附近，通过选取最小代价函数即可确定方位和俯仰角估计值。此即本文提出的多假设Taylor级数(MHTS)测向方法的基本思路。

下面给出测向算法的主要流程：

Step1：确定辐射源来波方向初始值θm=[αm,βm]T，m=1,2,…,M。初始时刻令m=1。

Step2：利用(15)式计算相位差关于θm的Jacobi矩阵Pm。

Step3：利用(17)式计算相位差预测值Θm，利用(19)式计算测量值和预测值之间的残差zm。

Step6：计算估计值对应的检验量Cm：

(20)

Step7：判断m若等于M则转入Step8，否则令m=m+1，转入Step2继续处理剩余初始值。

Step8：将检验量C(m)最小值对应的估计值作为视线矢量的估计值：

(21)

3 初值选取方法

上述算法中，关键是如何获得角度初始值。针对二维干涉仪阵的特点，进行初始值选取。首先选择利用具有一定夹角(如90°)和一定基线波长比(如10～20之间或最长的几组基线中)的2个模糊相位差φi和φl，以及方位安装角θi和θl。

根据φi和φl对应的基线长度di和dl确定模糊相位差各自的取值范围k∈[-di/λ,di/λ]，h∈[-dl/λ,dl/λ]。通过遍历模糊数k和h，根据相位差与来波方向的关系，计算得到初始值。

对每组模糊数k和h，由φi和φl以及对应的方位安装角θi和θl，计算无模糊相位差和系数矩阵：

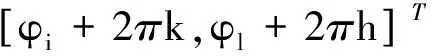
(22)

(23)

根据最小二乘可得：

(24)

若‖xkh‖大于1，不能构成单位视线矢量，因此舍去该组模糊数对应的初值。否则计算得到对应的方位和俯仰角的初始值：

(25)

(26)

由此可获得M≤(2di/λ+1)(2dl/λ+1)组方位和俯仰角初值。该初始化方法可推广到一维测向初值的选取。

4 仿真分析

通过计算机仿真，对不同干涉仪阵型以及一维和二维测向场景下，对本文测向方法性能进行验证。为评估测向性能，采用Monte Carlo重复试验统计定位误差。仿真中，定义方位角和俯仰角的均方根(RMS)误差为：

(27)

(28)

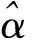
场景条件如下：一维测向中假设辐射源来波的方位角30°，信号频率3GHz。二维测向场景中，假设辐射源来波的俯仰角32°，其余参数与一维测向场景中相同。本文测向算法最大迭代次数为3。

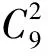
独立噪声模型下，两个接收通道通过9选2电子切换开关在不同切换时刻接收辐射源信号，在每组基线停留时间为1ms。相关噪声模型下，9个天线连接9个接收通道。各个通道测量得到初始相位，进而得到各组基线相位差。

仿真分析不同算法的二维测向性能。采用文献[10]中聚类测向方法，仿真中采用了夹角为4π/9的4组最长基线用于聚类，其余基线用于解模糊，并将各组基线中与聚类结果最接近的角度取均值作为估计值。采用文献[12]中的PSO方法用于相关干涉仪测向，利用本文方法中的代价函数进行，其中方位角搜索范围为[-π,π]，俯仰角搜索范围为[0,π/2]，粒子数量与本文方法初始点数量相同，最大迭代步数为400，惯性权重ω由0.9递减到0.6，学习率c1和c2均为2.1。

仿真图例中，Clstr表示聚类方法仿真结果； PSO表示PSO相关干涉仪方法仿真结果；MHTS表示本文算法仿真结果；CRLB表示测向误差克拉美-罗下限，计算方法可参见文献[18]；MSE表示测向理论均方误差。仿真中，测向估计值与真值的误差大于5倍理论误差则判定为测向模糊。

1)仿真一：独立噪声模型下二维测向

图4给出相位差独立噪声模型下，测量误差3°～40°范围内，不同算法的二维测向解模糊概率。

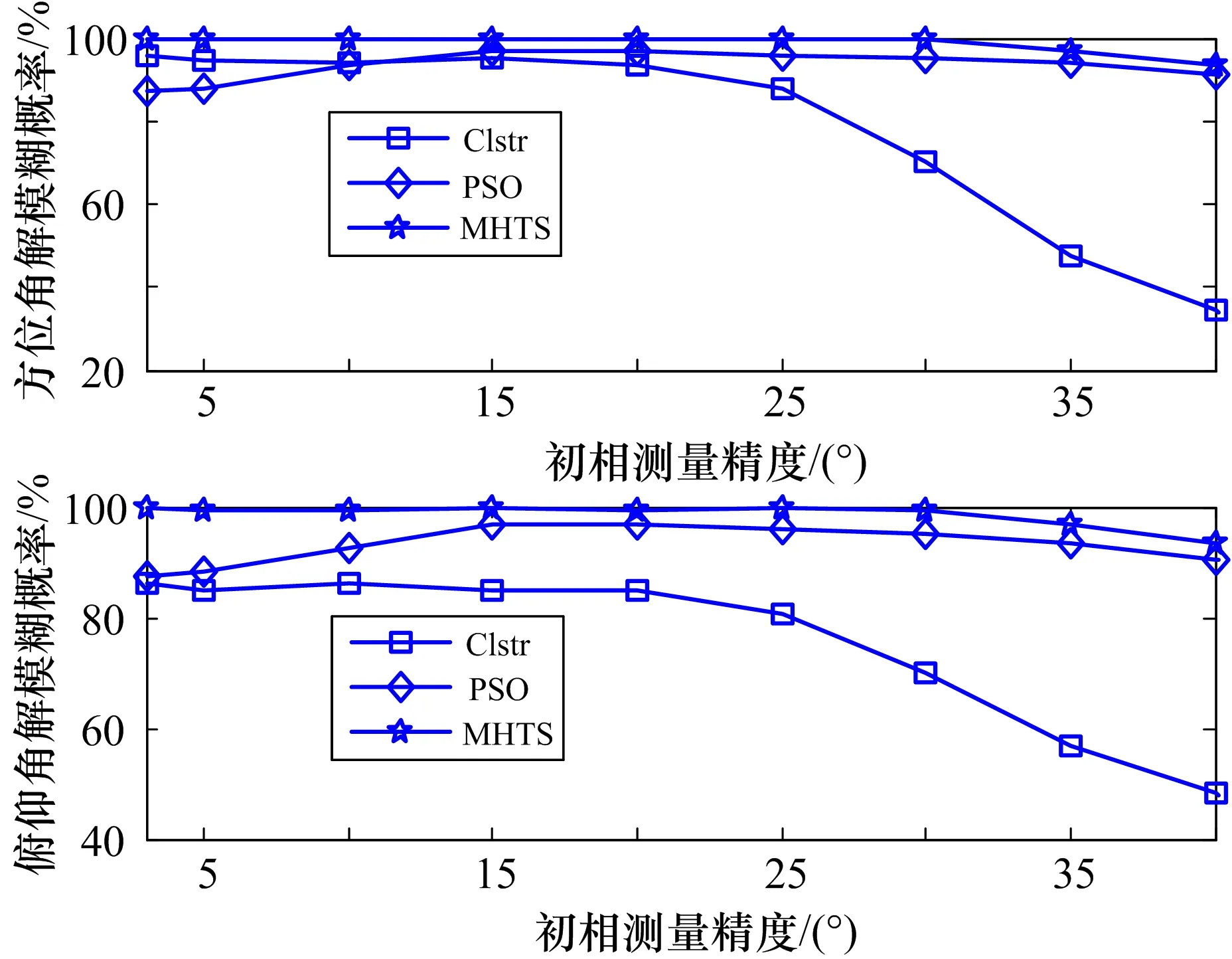
图4 独立噪声下不同算法二维测向解模糊概率

从图4可以看出，PSO方法由于随机搜索引起的个别局部极值，因此在相位差误差3°～30°范围内，解模糊概率不能达到100%。聚类方法本质上与相关方法相同，虽使用了多组基线，但仍未有效地使用所有基线。相位差误差3°～40°条件下，本文的测向方法解模糊概率优于聚类法和PSO方法。

图5给出相位差独立噪声模型下，测量误差3°～40°范围内，不同算法的二维测向精度。需要说明的是，图5和后文中的图7给出的统计误差，是剔除野值后得到的RMS误差。

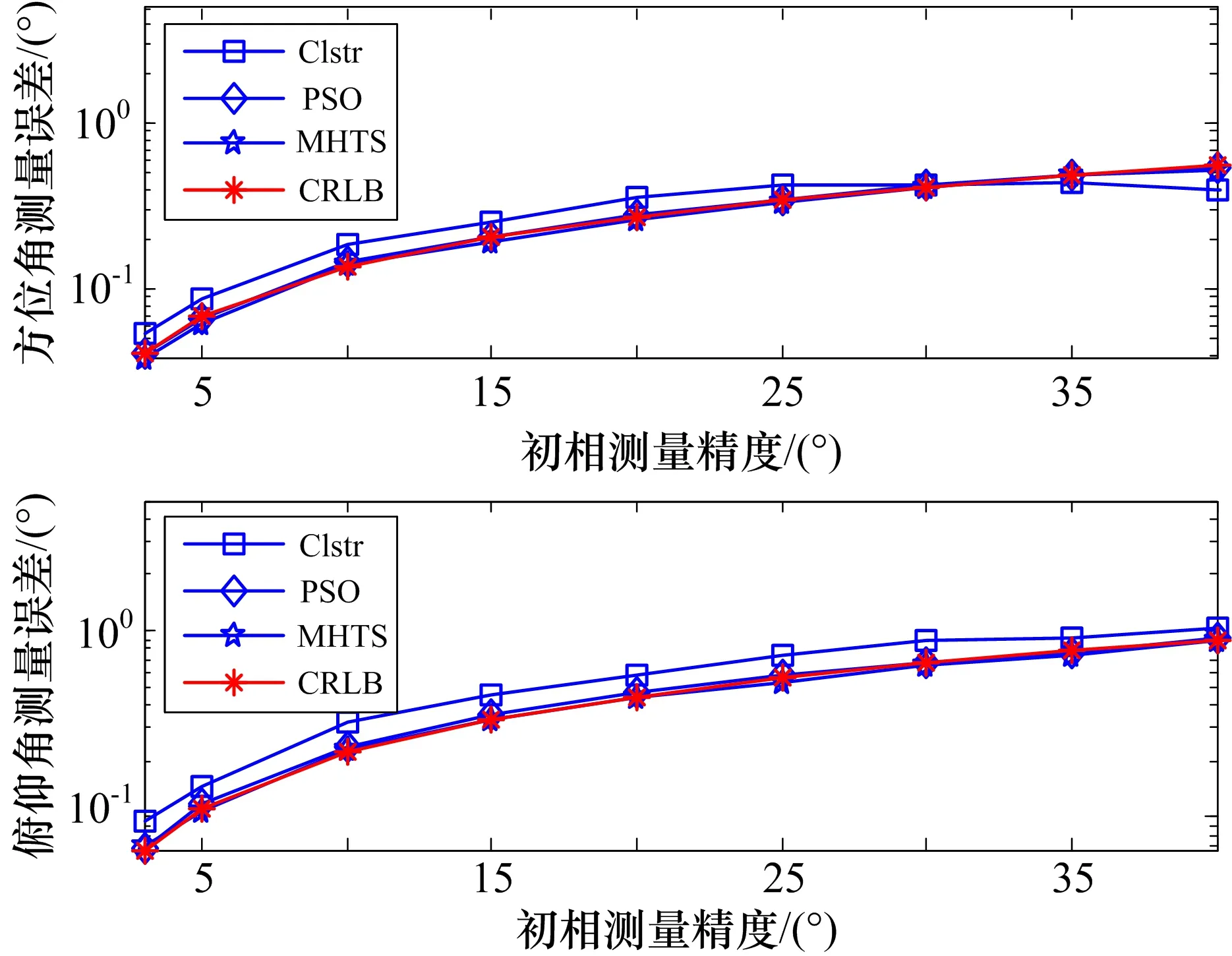
图5 独立噪声下不同算法二维测向性能

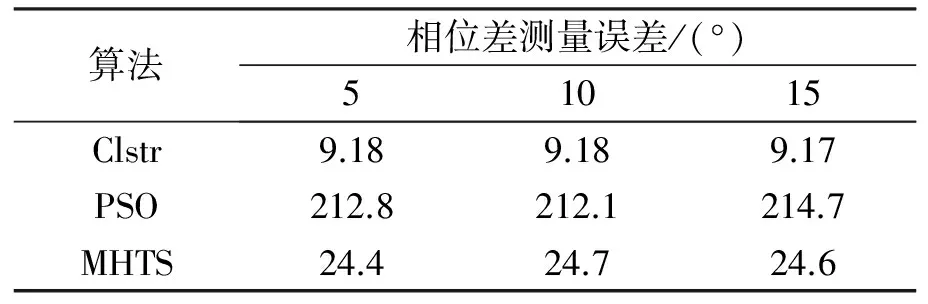
表1给出了二维测向方法仿真运算时间。

表1二维测向算法运行时间比较ms

算法相位差测量误差/(°)51015Clstr9．189．189．17PSO212．8212．1214．7MHTS24．424．724．6

计算机操作系统为Microsoft Windows XP，硬件配置为Intel®CoreTMi5 CPU 750@2.67GHz , 2.66GHz，内存3.24GB，使用Matlab®软件进行计算。

从表1和图5中可以看出， PSO方法运算时间高于其它方法一个数量级。聚类方法运算时间虽然优于本文方法，但未有效地使用所有基线，因此测向性能不能达到CRLB。本文方法在相位差误差3°～40°之间，方位角和俯仰角测量精度都可到达CRLB。

2)仿真二：相关噪声模型下二维测向

图6给出相位差相关噪声模型下，测量误差3°～30°范围内，不同方法的二维测向解模糊性能。

图7给出相位差相关噪声模型下，测量误差3°～30°范围内，不同方法的二维测向精度。

从图7可以看出，在相关噪声模型下，在剔除野值后，聚类方法和本文方法的测向精度相当，且都可接近理论测向精度；PSO方法在初相测向误差较小时，测向误差略大于理论误差。然而从图6可以看出， PSO方法仍然由于随机搜索引起的个别局部极值，导致解模糊概率不能达到100%；而本文方法的解模糊概率优于其它两种方法。

5 结束语

本文提出的一种适用于任意平面阵干涉仪的多假设Taylor级数(MHTS)测向方法，直接利用模糊相位差进行测向，无需事先解相位差模糊，对二维干涉仪几何构型无特殊要求。该方法利用相位差所包含的角度信息作为初值，采用Taylor级数方法进行计算，运算量适中。理论分析和数字仿真表明本文方法测向精度可接近理论测向精度。■

[1] Rong Yang, Pek Hui Foo, Boon Poh Ng, et al. RF emitter geolocation using amplitude comparison with auto-calibrated relative antenna gains [J]. IEEE Trans. on Aerospace and Electronic System, 2011, 47 (3): 2098-2110.

[2] Schmidt R. Multiple emitter location and signal parameter estimation[J]. IEEE Trans. on Antennas and Propagation, 1986, 34(3):276-280.

[3] Macphie RH, Tae Ho Yoon. On using the compound interferometer to obtain the power pattern of a conventional receiving array[J]. IEEE Trans. on Antennas and Propagation, 2009, 10(57):3356-3359.

[4] Ching-Sung Shieh, Chin-Teng Lin. Direction of arrival estimation based on phase differences using neural fuzzy network [J]. IEEE Trans. on Antennas and Propagation, 2000, 48(7): 1115-1124.

[5] Jacobs E，Ralston EW. Ambiguity resolution in interferometry [J]. IEEE Trans. on Aerospace and Electronic System, 1981, 17 (6): 766-780.

[6] 周亚强,皇甫堪. 噪扰条件下数字式多基线相位干涉仪解模糊问题[J].通信学报,2005,26 (8) :16-21.

[7] 曲志昱, 司锡才. 基于虚拟基线的宽带被动导引头测向方法[J]. 弹箭与制导学报,2007,27(4):92-95.

[8] 宋才水, 顾尔顺. 无模糊长基线干涉仪测角的设计[J]. 现代防御技术,2006,34(2):52-54.

[9] 张亮, 徐振海,熊子源,等. 基于圆阵干涉仪的被动导引头宽带测向方法[J]. 系统工程与电子技术,2012,34(3):462-466.

[10] 张春杰, 李智东. 非均匀圆阵天线模型解模糊误差研究[J]. 系统工程与电子技术,2012,34(8): 1525-1529.

[11] Wei Hewen, Shi Yunguang. Performance analysis and comparison of correlative interferometers for direction finding [C]∥Proc. of the IEEE International Conference on Digital Object Identifier, 2010:393-396.

[12] Frans Van de Bergh. A new convergent particle swarm optimizer[C]∥IEEE International Conference on Systems, Man and Cybernetics, 2002:96-101.

[13] 翟庆伟. 最小二乘法测向技术研究[J].无线电工程,2008,38(3):55-57.

[14] Cheng Yongqiang, Wang Xuezhi, Caelli T. Tracking and localizing moving targets in the presence of phase measurement ambiguities[J]. IEEE Trans. on Signal Processing, 2011, 59(8): 3514-3525.

[15] 李腾,郭福成,姜文利. 基于旋转干涉仪模糊相位差的多假设NLS定位算法[J].电子与信息学报,2012,34(4): 956-962.

[16] Kawase S. Radio interferometer for geosynchronous satellite direction finding[J]. IEEE Trans. on Aerospace and Electronic System, 2007, 43 (2):443-449.

[17] Wu Wei,Cooper CC, Goodman NA. Switched-element direction finding [J]. IEEE Trans. on Aerospace and Electronic System, 2009, 45(3): 1209-1217.

[18] Kay SM. Fundamentals of statistical signal processing, estimation theory [M]. Englewood Cliffs, New Jersey: Prentice Hall, 1993:30-36.