基于盲信号处理的MIMO雷达对抗

汤永浩，孙建东，黄和国，王成海

(中国航天科工集团8511研究所，江苏 南京 210007)

0 引言

MIMO雷达由于其发射波形多样性带来的额外自由度，能够提高系统目标检测、参数估计以及抗干扰等性能[1-2]。根据阵元配置，MIMO雷达可分为：集中式MIMO雷达和分布式MIMO雷达。集中式MIMO雷达阵列配置与传统相控阵类似，且同时发射不同的信号波形。利用波形多样性信息，集中式MIMO雷达在接收端能够依靠信号传输通道的正交性，获取额外自由度，形成虚拟大口径天线以提高雷达的空间分辨率[3]。分布式MIMO雷达的发射和接收阵元的间距都很大，可认为每个阵元发射的信号之间都是相互独立的。这种配置的MIMO雷达能够收集目标的空间多样性信息，缓解由于目标闪烁引起检测性能下降等问题[4]。

尽管目前针对MIMO雷达的研究仍然处于理论研究为主、少量实验室验证阶段，但已有不少学者在MIMO雷达对抗方面展开了相关研究工作。文献[5～6]对MIMO系统的盲源个数估计进行了研究。文献[7]等基于盲信号分离提出了对MIMO雷达信号的侦察与识别方法，但并未考虑噪声的影响。针对MIMO雷达信号的多样性与复杂性，本文开展了MIMO雷达侦察与干扰技术初步研究，给出了一种基于盲信号分离的MIMO雷达对抗分布式系统的原理框架，初步研究了该框架下的MIMO雷达信号分选识别方法。同时，介绍了利用盲信号处理的结果、结合数字射频存储(DRFM)技术，对单双基地MIMO雷达进行有效欺骗干扰的可行手段，并给出了仿真结果。

1 信号模型

MIMO雷达的概念起始于通信理论中的多通道模型，与传统雷达的显著区别在于其不同的阵元能够发射任意的波形、接收阵元能够同时处理接收到的不同信号(通常为正交信号)。不妨假设一部具有M个发射阵元和N个接收阵元的MIMO雷达，天线发射任意信号sm(t),m=1,…,M。同时，假设空间远场位置存在一个目标，则MIMO雷达接收回波信号模型可以描述为：

y(t)=αGKTs(t)+n(t)

(1)

式中，α为目标散射系数，G为N×1维接收通道传输系数，K为M×1维发射通道传输系数，s(t)=(s1(t),s2(t),…,sM(t))T为M维信号矩阵，n(t)为N×1维噪声向量。值得注意的是，式(1)为MIMO雷达的通用信号模型，对于集中式和分布式MIMO雷达，其区别在于G和K的定义不同。对于集中式MIMO雷达而言，G和K即为明确可知的相应阵列天线的接收和发射导向性矢量。

类似地，不妨假设MIMO雷达侦察系统具有N个接收机，参考式(1)可得侦察系统的输出信号为：

y(t)=Hs(t)+n(t)

(2)

式中，H为N×M维传输通道系数矩阵。比较分析式(1)和式(2)可知，MIMO雷达侦察系统尽管具有与MIMO雷达相似的信号模型，但是雷达信号s(t)与传输矩阵H均为未知数。对于MIMO雷达对抗系统来说，不仅要能判断出是否为MIMO雷达体制，而且还要能够掌握MIMO雷达的具体细节，如信号参数、阵列配置等，从而对MIMO雷达实施有效干扰，其关键在于对MIMO雷达波形的分选与识别。因此需要突破常规雷达信号侦察手段，对混叠在一起的复杂MIMO雷达信号进行盲分离处理。

2 MIMO雷达盲信号分离问题

2.1 问题建模

近年来，盲信号处理算法已经在无线通信、语音处理、神经网络等方面有了广泛应用研究。“盲”主要指源信号及其混合方式均未知，而盲信号处理算法则是指仅依靠观测获得的混合数据恢复出源信号及其混合矩阵的一类算法。按照源信号混合方式，盲源分离研究可分为瞬时线性混叠、卷积混叠及非线性混叠盲分离3类。MIMO雷达信号的盲分离恰恰属于最简单的瞬时线性混叠方式，其模型为：

y(t)=As(t)

(3)

x(t)=Wy(t)

(4)

式中，s(t)为未知源信号矩阵，A为混合矩阵，y(t)为已知观测信号矩阵，W为分离矩阵，x(t)为分离信号。理想情况下，满足W=A-1，即意味着能够获得未知源信号的最佳估计。

目前关于盲源分离算法研究很多，本文主要分析超定盲分离的情况。独立成分分析(ICA)是求解超定盲分离问题的成熟算法，针对MIMO雷达信号盲分离问题的求解有以下要求限制：

1) 源信号的各个分量为相互统计独立的零均值平稳随机变量；

2) 混合矩阵列满秩，且观测信号维数不少于源信号维数；

3) 混合信号中最多只能有一个高斯分量。

在满足上述3个条件的假设下，ICA算法能够实现对源信号的分离及混合矩阵的估计。MIMO雷达通常发射正交波形，这是MIMO雷达的显著特征，因此条件1)显然满足。为了满足条件2)，可以采用分布式多接收站来实现，即在空间不同位置进行多点采样，利用空间分集特性获得列满秩的混合矩阵，同时节点数需要大于源信号数。比较式(2)和式(3)模型可以发现，对MIMO雷达盲信号处理问题应用ICA算法，无法避免高斯噪声带来的影响，并且高斯噪声维数与观测信号维数相同，因此无法满足条件3)。不妨对式(2)中的MIMO雷达侦察信号模型进行一定的变换，即改写为：

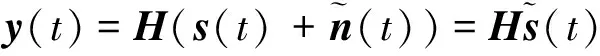
(5)

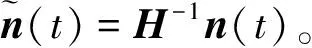
2.2 盲信号分离算法

目前盲信号分离的算法较多，其中快速不动点ICA算法(FastICA)具有收敛速度快、精度高等特点，因此本文以FastICA算法为例简要分析。基于FastICA算法[8]的MIMO雷达盲信号分离算法如下：

1) 对观测数据进行降噪或降维处理，利用PCA、MDL或AIC等准则[9]估计独立成分个数m；

2) 对数据进行白化处理，并选择非高斯性度量函数为gy=y3；

3) 选择具有单位范数的初始化向量wp(随机选择)；

5) 对分离向量进行正交化和标准化：

6) 如果wp尚未收敛，返回步骤4)；

7)p=p+1，若p≤m，返回步骤4)；

8) 计算分离信号x(t)=Wy(t)，W=(w1,w2,…,wm)T。

3 基于盲信号处理的MIMO雷达对抗系统,

3.1 系统架构

基于盲信号处理的MIMO雷达对抗系统示意框图如图1所示。该系统采用N个接收机对MIMO雷达进行信号侦收，其具体实现方式可以为分布式布阵，如无人机集群侦察系统，也可以由一架侦察飞机在飞行路径中的多个位置进行多次分时采样获得。截获数据可采用分布式或集中式进行处理。根据盲信号处理的结果，对分离出的信号分别进行聚类、融合等处理。根据侦察处理结果，结合数字射频存储(DRFM)技术，可对干扰信号的各独立分量进行单独调制，实现对MIMO雷达的所有通道进行有效干扰。若综合考虑不同信道的相关性，合理调制各个干扰分量，可实现对MIMO雷达在时间和空间上具有良好相关性特征的欺骗式干扰。

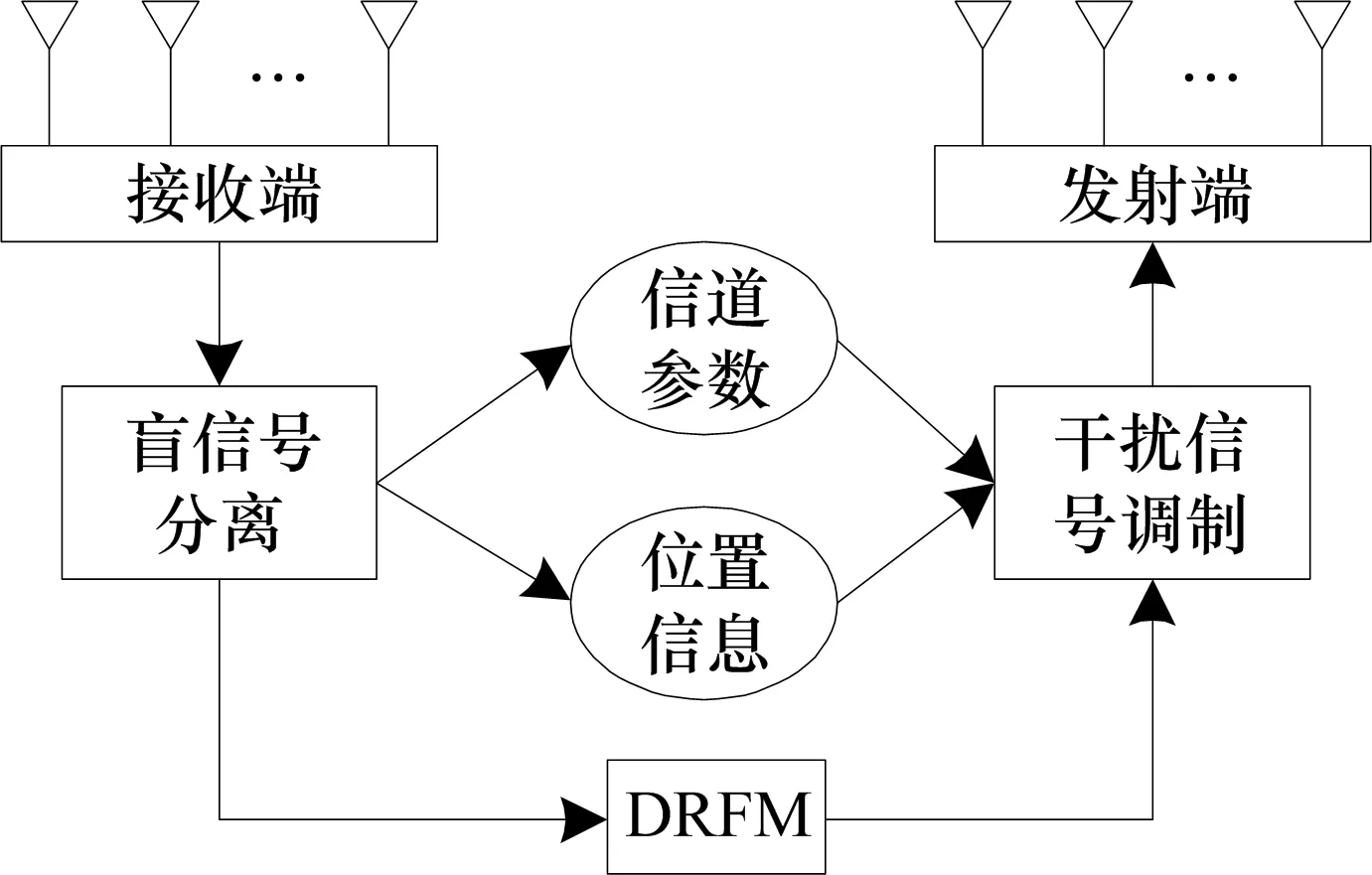
图1 基于盲信号处理的MIMO雷达对抗系统示意图

该系统对MIMO雷达的对抗处理步骤如下：

1) 对截获的信号经由盲信号分离模块处理，提取各个信号的频率、脉宽、幅度、波形调制等信息；

2) 对信号脉冲参数进行分选，对辐射源进行识别、定位等计算；

3) 通过信号相关性和信道估计，判断MIMO雷达工作体制和模式；

4) 判断MIMO雷达威胁程度，选择合适的干扰方式和样式进行干扰；

5) 监测MIMO雷达信号变化，调整干扰策略。

3.2 基于分离信号的MIMO雷达识别

按照目前理论研究的主流观点，MIMO雷达主要有集中式和分布式两大类。两种MIMO雷达无论是在阵列布局和发射波形，还是在接收信号处理方式上，都存在着明显的差别。其中，分布式MIMO雷达各个发射阵列分布范围较广，其发射信号的正交性可以由频率分集、空间分集或波形分集等得以保证。集中式MIMO雷达在传统相控阵雷达的基础上发展而来，因此其发射阵列与相控阵类似，但是其仍然可能被布置成单基地或双/多基地雷达。此外，传统的集中式MIMO雷达每个阵元发射正交信号，但是近年来有不少研究学者提出了发射部分相关信号的MIMO雷达体制，因而集中式MIMO雷达具有发射功率均匀分散的搜索模式和发射功率相对集中的跟踪模式两种工作模式。因此，对抗方若要对MIMO雷达实施精确、有效的干扰，必须要先对截获的信号进行仔细分析，对雷达工作体制及工作模式进行识别。

采用图1所示的处理框架，分离出MIMO雷达所采用的所有正交波形，依据正交波形数量即可推断出MIMO雷达采用的通道数(阵元天线或子阵数量)。对分离出的单个正交波形进行单独检测，利用多站点时差定位、交叉定位等技术，则可对相应的发射阵列天线位置分别进行估计。融合所有定位结果，可判断MIMO雷达属于集中式还是分布式配置；同时，定位结果还可以帮助对抗方进行精确、有针对性的电子干扰。此外，利用分离矩阵对发射信道参数的估计，还能够判断集中式MIMO雷达的工作模式。这是因为集中式MIMO雷达工作于搜索模式时，雷达能量信号空间均匀分散，信噪比较低，信道参数变化不大；而当其工作于跟踪模式时，波束具有高增益，信道参数与角度信息具有强相关性。

3.3 单双基地MIMO雷达的干扰

单双基地MIMO雷达体制上属于集中式MIMO雷达，因而具有与相控阵类似的天线阵列结构。该体制的MIMO雷达在搜索模式时，通常采用正交发射波形，发射端不进行波束形成，而在接收端进行接收波束形成和虚拟发射波束形成，称之为收发联合波束形成。这种MIMO雷达最为显著的一个优势为：能够利用发射信号传输通道的正交性，进行收发联合波束形成，获得更大的虚拟口径，以提高系统的角度分辨率。其点目标接收信号模型可以表示为：

z(t)=αbθraT(θt)s(t)+n(t)

(6)

式中，α为目标散射系数，b(θr)为接收阵列导向性矢量，θr为目标相对接收阵列的方位角，a(θt)为发射阵列导向性矢量，θt为目标相对发射阵列的方位角。通过对接收信号z(t)进行适当处理，如MUSIC、ESPRIT算法等，可以获得对目标方位角θt和θr的准确估计。

分析式(6)可以发现，若采用传统调制转发式欺骗干扰，即对混合信号aT(θt)s(t)进行调制转发，调制系数将会与散射系数α类似，不会对MIMO雷达的DOA和DOD估计造成影响。而采用本文提出的盲信号处理架构，可实现对所有正交信号通道进行单独调制，即对s(t)的每一行元素进行不同的调制，即MIMO雷达接收到的干扰信号模型为：

z(t)=αb(θr)(a(θt)diag(φ1,φ2,…,φM))Ts(t)+n(t)

(7)

式中，φm表示对m个正交信号的调制系数。由式(7)可知，发射导向矢量受到干扰调制系数的影响，MIMO雷达的DOD估计将会产生较大误差，从而收发联合波束形成将会受到较大的角度欺骗干扰影响。

4 数值仿真分析

本节从数值仿真上验证MIMO雷达对抗系统采用盲信号处理及角度干扰的有效性。

假设一集中式MIMO雷达采用M=4个发射接收阵元，发射频分正交线性调频信号，起始频率分别为10MHz，每个信号间隔5MHz，带宽均为4MHz，脉宽为80μs，信噪比设置为20dB。侦察方采用N=5个接收站进行分布式侦收，采用2.2节中的算法对混叠的MIMO雷达信号进行盲分离。图2～4分别给出了MIMO雷达源信号、某路接收到的空间混合信号以及盲分离后的信号的时频分析结果。为了方便比较，图2和图4中将4路正交信号拼接画在了同一图中。分析可知，尽管分离信号的顺序与原始信号不一致，但是该算法能够在源信号和混合矩阵均未知的情况下，较好地实现信号分离，并且从图5可知，分离信号保持了较好的自相关性(如图5(a)～(d)所示)和互不相关性(如图5(e)～(j)所示)。

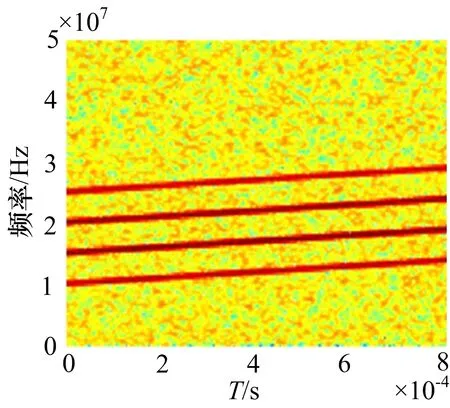
图3 某路接收混合信号时频分析图

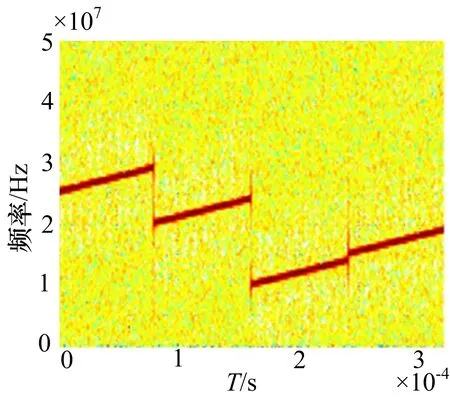
图4 分离信号时频分析图

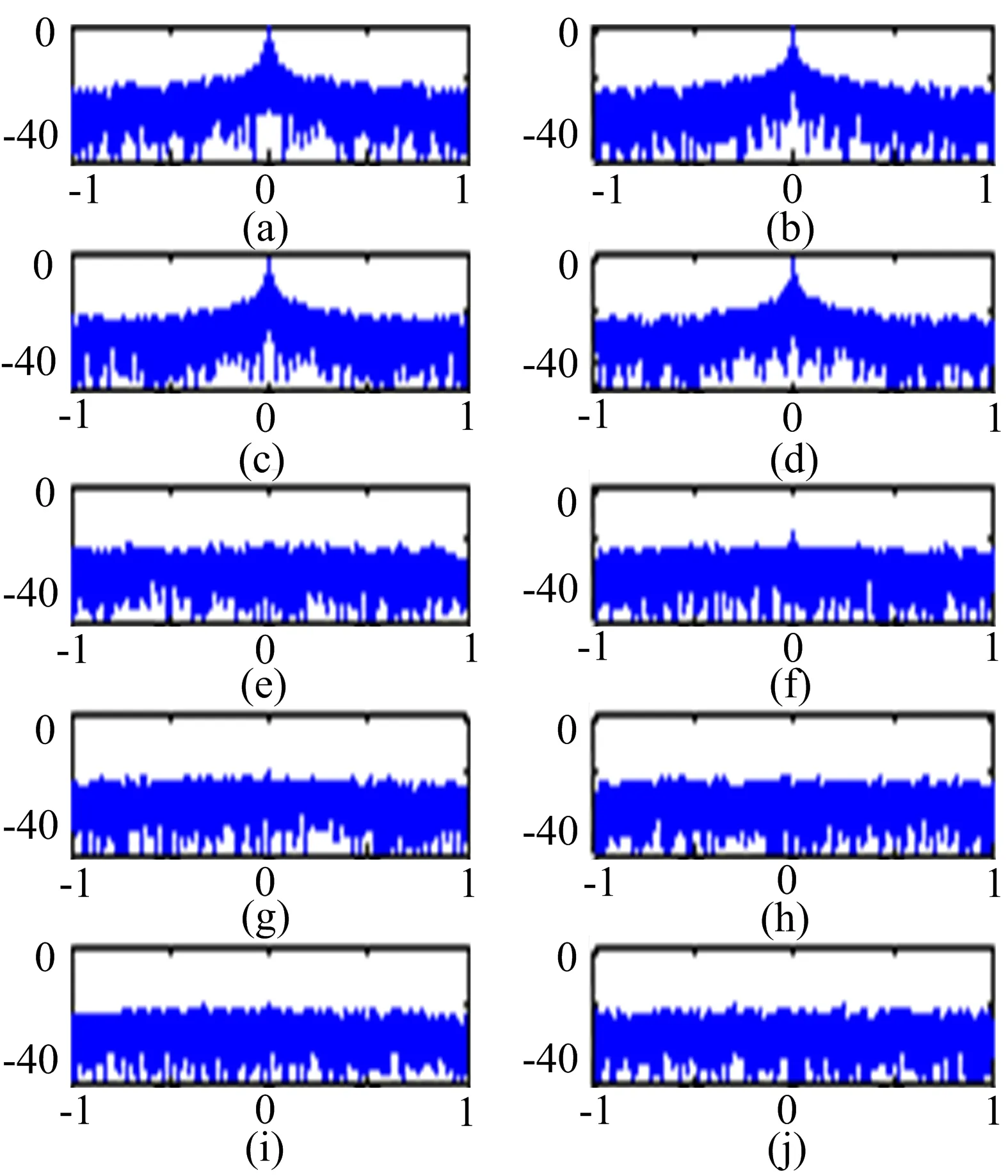
图5分离信号的相关性

MIMO雷达通常在接收端利用收发联合虚拟阵列的信号处理方式，并采用诸如MUSIC、ESPRIT等算法进行空间谱估计。根据本文提出的MIMO雷达对抗架构，对分离获得的信号进行单独的随机相位调制，实现对MIMO雷达收发正交通道的干扰，即雷达接收端接收到的信号如式(7)所示，在发射导向性矢量中引入了相位干扰φm，经过MUSIC算法处理后，本应在-10°方向形成尖锐的谱峰，却得到了杂乱无章的谱估计图，如图6所示。这就说明，本文提出的方法，能够对MIMO雷达进行有效的角度干扰。

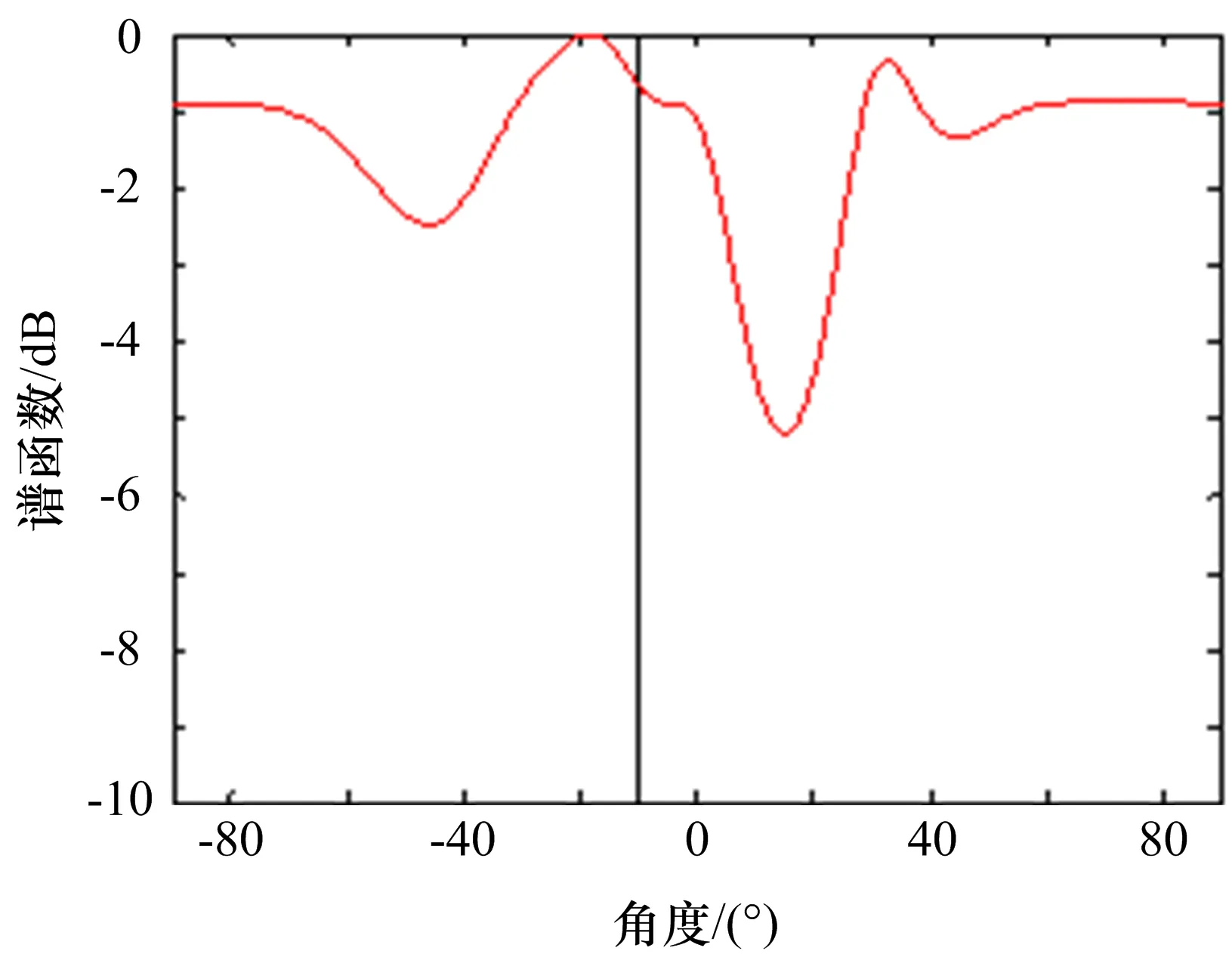
图6 MIMO雷达接收端进行收发联合谱估计结果

5 结束语

本文简要分析了MIMO雷达与MIMO雷达侦察的信号模型，对比了其区别，提出了基于盲信号处理的MIMO雷达对抗系统模型，对MIMO雷达侦察与干扰方法进行了一定的分析，并给出了仿真结果。但是，针对噪声背景下的混叠信号盲分离算法以及分布式对抗原理系统实现等问题，仍亟待后续深入研究。■

[1] Fishler E, Haimovich A, Blum R,et al.MIMO radar:an idea whose time has come[C]∥Proc.IEEE Radar Conf., 2004:71-78.

[2] Daum F, Huang J. MIMO radar: snake oil or good idea?[J].IEEE Aerospace and Electronic Systems Magazine,2009,24(5)：8-12.

[3] Li J, Stoica P. MIMO radar with co-located antenna: review of some recent work[J]. IEEE Signal Processing Magazine, 2007,24:106-114.

[4] Haimovich M, Blum RS, Cimini LJ. MIMO radar with widely separated antennas[J].IEEE Signal Processing Magazine, 2008,25,:116-129.

[5] Hassan K, Nsiala Nzéza C, Gautier R ,et al.Blind Detection of the Number of Transmitting[C]∥11th International Conference on ITS Telecommunications Antennas for Spatially-Correlated MIMO Systems, 2011.

[6] 胡建华.面向MIMO系统的发射天线数目盲估计[D].西安:西安电子科技大学, 2013.

[7] 方健.基于盲源分离的MIMO雷达侦察与识别[D].西安:西安电子科技大学, 2014.

[8] 海韦里恩,卡尔胡恩. 独立成分分析[M].北京：电子工业出版社，2014.

[9] 冷巨昕.盲信号处理中信源个数估计方法研究[D].成都：电子科技大学, 2009.