大坝服役性态安全监控的GA-RBF组合模型
杜 辉 赵二峰 郭 珅 姓海涛 张 敏
(1. 河海大学 水文水资源与水利工程科学国家重点实验室,南京 210098;2. 河海大学 水资源高效利用与工程安全国家工程研究中心,南京 210098;3. 四川省水利水电勘测设计研究院,成都 610000;4. 南京市溧水区水务局,南京 211200)
神经网络具有很强的非线性逼近能力,近年来被越来越多的应用在非线性拟合领域内,并取得了丰硕的成果[1].其中应用最为广泛的是径向基函数神经网络.径向基函数神经网络(Radial Basis Function Neural Network,RBFNN)是一种3层前馈神经网络,具有单个隐层结构.RBF神经网络有极高的局部最佳非线性逼近能力[2];比其他神经网络更简单的结构[3];在学习过程中,RBF网络可以调整局部神经元个数,具备较高的学习效率[4].诸多特点使RBF网络得到了广泛的应用[5].张伟储等[6]将RBF网络应用于大坝应变预报中;王德文等[7]将RBF网络应用于大坝位移监控中,都取得了很高的预测精度.任何事物都有两面性,有优点就有缺点,RBF网络也同样存在缺点.如果目标函数十分复杂,在用普通的RBF网络进行训练时,容易陷入局部最优.而遗传算法是一种模仿生物自然进化过程的算法,可以通过全局并行搜索摆脱局部最优的困扰,搜索到目标函数最优解[8].而大坝服役性态影响因素广泛,干扰因素众多,具有非线性、变量多的特性,难以准确的用普通数学模型刻画其服役性态.为了能更好的模拟大坝服役过程,分析服役机理,有效的对大坝服役过程进行预报,并提前预警,本文在RBF网络的基础上,用遗传算法对其网络参数进行优化,并将该新模型应用于大坝服役性态安全监控中.
1 RBF神经网络
径向基函数神经网络为3层神经网络.基本构成为输入层、隐含层和输出层.各层单元数分别设为m、l、n,有n个输出值的RBF神经网络结构如图1所示.相邻层的两个神经元可以互相连接,并从低层向高层传输信号.输入数据通过非线性函数由低维的输入层变换到高维的隐含层,然后再从高维空间线性映射到输出层.从理论上讲,该网络可以拟合任意连续函数,并且精度取值可以任意.径向基函数神经网络的拓扑结构和参数对网络性能有很大的影响作用.通常来说,m由输入变量个数确定,n由输出变量个数确定,而l根据问题设定确定.隐含层的传输函数称作径向基函数,常用的传输函数有高斯函数、多二次函数和逆多二次函数.本文取高斯函数为传输函数.
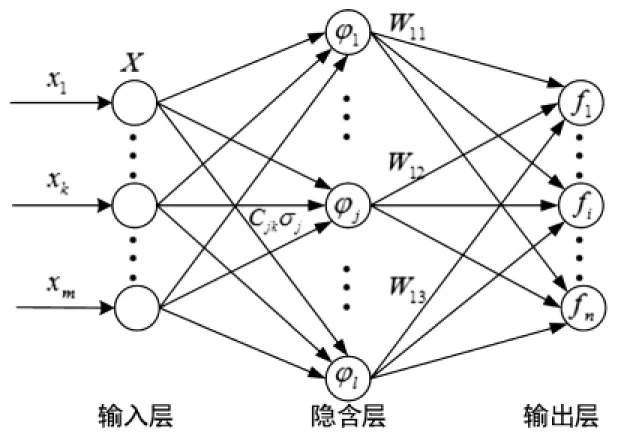
图1 RBF神经网络结构图
选取p个样本,若给定输入模式Xk=(x1,x2,…,xm),则隐含层单元输出由公式(1)得到:
(1)
式中,φ(·)为高斯函数;Cj=(Cj1,Cj2,…,Cjk,…,Cjm)是第j个隐层节点的中心矢量,其维数等于输入变量的个数;σj是第j个隐层节点的中心宽度.
RBF网络由隐含层通过公式(2)得到输出值:
(2)
式中,fi(X)是第i个输出层的输出;Wij为连接权值.
为了更好的得到RBF网络参数,本文用遗传算法优化Cjk、σj和Wij.
2 遗传算法
遗传算法(Genetic Algorithm,GA)起源20世纪60年代,是模拟生物在自然环境中的遗传和进化而形成的一种在问题空间进行全局并行的、随机的搜索优化,使得种群全局最优收敛的算法[9].
遗传算法的基本操作分为染色体编码、适应度函数设计、选择及交叉和变异.基本操作步骤如下:
①染色体编码.本文中由于需要对较大实数进行操作,用实数编码较为方便.每一个待寻优的参数表示一个基因,所有待寻优的参数组合成一条染色体,每条染色体都对应一个完整的RBF网络.单个染色体可表示为:C11C21…Cl1C12C22…Cjk…C1mσ1σ2…σj…σlW11W21…Wn1W12…Wij…Wnl,种群规模为p,即共有p个染色体.
②适应度函数设计.我们取输出值与网络预测值误差平方和的倒数作为染色体质量的评判函数,所有个体的适应度值均为非负.单个染色体适应度为:
(3)
式中,fi是网络输出值;yi是目标值.
③选择操作.选择操作是从旧群体中以一定的概率选择优良个体组成新的种群,并繁殖下一代,也就是按照一定条件的复制操作.第t个染色体被选择的概率为:
(4)
式中,Ft为第t个个体的适应度.本文采用轮盘赌的选择方法.先计算出各个个体的Pt,然后随机产生一个r∈[0,1]的数,若P1+P2+Pt-1 ④交叉和变异.交叉是两个个体进行性状组合,产生新的基因型个体.交叉是产生新个体的主要途径.由于该算法对Cjk、σj、Wij进行优化,采用多点交叉法较为妥当.从种群中按照概率随机选择两个个体,按交叉概率分别对Cjk、σj、Wij这3种类型的基因部位分别产生一个交叉点,进行交叉操作.交叉概率Pc一般取0.65~0.9.变异是产生新个体的次要手段.具体操作是以一定的概率从父代种群选择1对个体,再分别对3种类型的基因值以一定的概率随机改变.变异操作可以有效的防止有用基因在进行遗传操作中丢失.变异概率Pm一般取0.01~0.1. 为了更好的用RBF网络对大坝服役性态进行模拟,我们用遗传算法优化RBF神经网络参数.基本思路是先用遗传算法训练RBF网络的Cjk、σj和Wij,找到一个较优解,然后将结果作为初始参数对RBF网络进行训练.算法的主要步骤如下: ①对原始数据进行归一化处理,便于后续操作,并选取合适的数据作为训练样本. ②染色体采用实数编码,单个染色体包含m+n+l个基因,并生成初始种群P(g),进化代数记为g=0,并确定最大进化代数G. ③解码染色体,得到Cjk、σj、Wij,由式(2)计算输出层值fi(X). ④用式(3)计算得到每个个体的适应度值F,以此评价网络的性能,若满足终止条件g>G,则结束,否则转步骤⑤. ⑤计g=g+1,并进行遗传操作. a)根据个体的适应度F,用轮盘赌法选择个体进入下一代种群P(g+1),适应度值大的个体可以直接复制到子代,同时对其他染色体进行两两配对. b)以概率Pc对父代染色体进行交叉操作,得到新的染色体. c)以概率Pm对选定的染色体三种基因进行变异操作,获得新的染色体. ⑥通过步骤⑤产生新种群,转入步骤④,直到g>G则结束计算. 具体算法流程如图2所示. 图2 GA-RBF算法流程 某双曲拱坝位于四川雅砻江,坝体的具体数据见表1.本算例取13号坝段正垂线坝顶测点PL13-1测点2014年1月到2016年11月径向位移监测资料进行分析. 表1 大坝参数 图3 上游水位及PL13-1径向位移实测过程线 本算例中,选取上述的水压、温度、时效方面的8个因子作为输入变量,径向位移y作为输出变量,组建成输入层为8、输出层为1、隐含层为8的RBF网络.用遗传算法优化Cjk、σj、Wij,将优化后的Cjk、σj、Wij作为RBF网络初始值,进行训练、预测.2014年1月到2016年11月的监测数据共有139组,选取2016年1月24日前共计100组数据作为训练样本,2016年1月24日至2016年11月的39组数据作为测试样本.通过不断实验,综合分析考虑,遗传算法的各项参数设置见表2.用标准的RBF模型和GA-RBF模型分别进行训练及预测,并做出曲线图,如图4所示.两种模型比较结果见表3. 表2 模型参数 图4 两种模型拟合曲线 通过比较模型的均方误差(MSE)和相关系数(R)来确定这两个模型的优劣.均方误差按下式计算: (5) 式中,f为神经网络输出值,y为监测值. 表3 两种模型比较 从图4可以看出:GA-RBF模型比标准RBF拟合效果好,GA-RBF模型预测效果比标准RBF模型更为接近实际测值.从表3可以看出:在拟合部分,RBF模型的均方误差值略优于GA-RBF模型,在预测部分,GA-RBF模型的均方误差值远优于RBF模型,对所有样本数据来看,GA-RBF模型仍优于RBF模型较多.此外,GA-RBF模型的相关系数也优于RBF模型的相关系数.综合均方误差和相关系数分析,可以表明本文用遗传算法对RBF神经网络参数进行优化可以提高RBF网络的拟合及预测精度,该模型可以应用在大坝的位移监控方面. 近年来,在大坝服役形态安全监控方面的研究越来越多,并取得了很好的研究成果.越来越多的新方法、新理论被应用于大坝安全监控方面.其中以神经网络最为火热.本文介绍了RBF神经网络以及遗传算法的原理,并讨论了各自的优缺点.为了解决标准RBF网络容易陷入局部最优,本文提出了一种新的大坝服役性态安全监控模型,即用遗传算法优化RBF网络的Cjk、σj和Wij.该组合算法模型充分发挥了遗传算法全局寻优能力,可以有效预防RBF陷入局部最优.将此模型用于拟合大坝服役形态的位移过程,结果表明,GA-RBF网络的各项拟合指标均优于标准RBF网络,使得RBF神经网络可以更加有效地用于大坝非线性系统服役性态的建模分析.本文的研究内容还有不足之处,可以在此基础进行更为深入、系统的研究,得到更好的安全监控模型. [1] 司春棣,练继建,郑 杨.土石坝渗流安全监测的遗传支持向量机方法[J].水利学报,2007,38(11):1341-1346. [2] Park J,Wsandberg J. Universal Approximation Using Radial Basis Functions Network[J]. Neural Computation,1991(3):246-257. [3] Lee S, Kil R M. A Gaussian Potential Function Network with Hierarchically Self-organizing Learning [J]. Neural Networks,1991,4(2):207 - 224. [4] Moody J, Darken C J. Fast Learning in Network of Locally-tuned Processing Units[J]. Neural Computation, 2014,1(2):281-294. [5] 乔俊飞,韩红桂.RBF神经网络的结构动态优化设计[J].Acta Automatica Sinica, 2010, 36(6):865-872. [6] 张 伟,储冬冬,余新洲.RBF神经网络在大坝应变预报中的应用[J].人民黄河,2011,33(2):124-125. [7] 王德文,李智录,卢瑞章.RBF神经网络在线学习方式及其在大坝位移监测中的应用[J].西北农林科技大学学报(自然科学版),2006,34(12):226-230. [8] 姜鹏飞,蔡之华.基于遗传算法和梯度下降的RBF神经网络组合训练方法[J].计算机应用,2007,27(2):366-368. [9] 赵志刚,单晓虹.一种基于遗传算法的RBF神经网络优化方法[J].计算机工程,2007,33(6):211-212. [10] 顾冲时,吴中如.大坝与坝基安全监控理论和方法及其应用[M].南京:河海大学出版社,2006.3 RBF网络的遗传算法优化
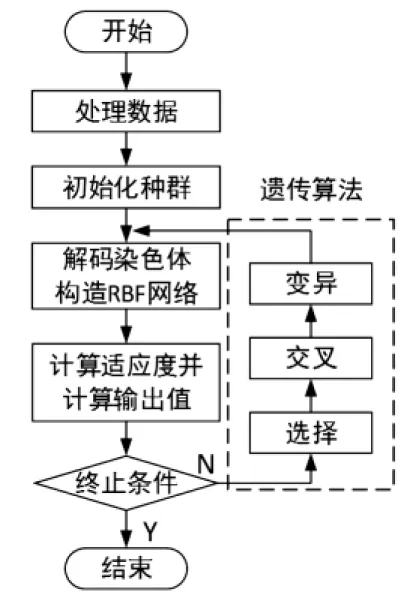
4 工程实例


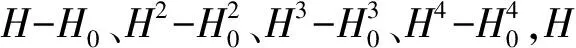


5 结 语

