改进的Poyting-Thomson岩石蠕变模型研究
杨广雨 王 伟 赵 腾 李学浩 秦志军
(1. 河海大学 岩土力学与堤坝工程教育重点实验室,南京 210098;2. 河海大学 岩土工程科学研究所,南京 210098; 3. 山西省交通规划勘察设计院, 太原 030012)
在岩土工程中,岩石流变是影响着工程安全稳定性的重要因素,因此岩石流变的研究也就显得越来越重要,其中元件模型是研究岩石流变性质的重要工具.传统的力学元件无法有效地模拟岩石加速蠕变阶段的蠕变特性,因此很多学者在已建立的岩石流变模型的基础上通过引进可以模拟加速蠕变特性的非线性元件,然后将非线性元件与传统流变模性进行适当地组合,从而能够很好地模拟岩石的3个阶段的蠕变过程.
目前,对岩石非线性流变阶段的元件模型研究已经取得了一定的成果,康永刚等[1]构建一种非牛顿体特性的力学元件,然后利用这些元件建立蠕变模型,很好地模拟了加速蠕变过程;周家文[2]等在广义Bingham模型的基础上结合能反映岩石加速蠕变特点的非线性函数,从而可以较好地模拟岩石加速蠕变特性;殷德顺等[3]通过引进Riemann-Liouville分数阶微积分算子理论,构造出一种可以反映岩石加速蠕变特性的力学元件;李成波[4]等提出了一种非定常参数粘弹性模型,从而较好地模拟岩石非线性蠕变过程;朱昌星等[5]提出了一种黏滞系数为非定常参数的岩石蠕变模型,该模型能够反映岩石加速蠕变特性流变模型;徐卫亚等[6]构造了一种非线性黏弹塑性力学元件,并由此建立了"河海模型",该模型能够很好地模拟了岩石加速蠕变特性.宋勇军等[7]构造了一种含有分数阶的软体元件即FC元件,该元件能够较好地描述岩石加速蠕变阶段的力学特性;曹平等[8]通过结合流变力学理论,对传统的黏性元件进行改进,从而能够很好地反映岩石加速蠕变特性;曹文贵等[9]通过引用损伤理论来模拟岩石加速蠕变;康永刚等[10]通过将一种非定常黏壶替换伯格斯模型中的定常黏壶,从而有效地模拟岩石加速蠕变阶段的岩石特性.本文通过引进一种非线性黏塑性元件并将其进行改进,然后将此改进后的元件与饱依丁-汤姆逊体(Poyting-Thomson)进行串联,建立起能够反映岩石蠕变全过程的蠕变模型,并结合岩石蠕变试验数据对其进行验证.
1 模型的建立
1.1 传统的Poyting-Thomson模型
经典的Poyting-Thomson模型是由一个Maxwell体与一个胡克体并联组成,该模型不仅结构形式简单,而且可以较好地模拟岩石蠕变的前两个阶段,同时由于模型中有着两个胡克体并联的结构形式,所以可以反映岩石在受力瞬间所产生的初始弹性变形,Poyting-Thomson力学模型如图1所示.

图1 Poyting-Thomson流变模型
(1)

根据其本构方程再结合Laplace变换可以求得相应的蠕变方程(具体的推导过程见下文),当应力为σ0并保持不变时,可以推求模型的蠕变方程为
(2)


图2 Poyting-Thomson蠕变曲线示意图
由上图2的模型蠕变曲线特点可知,传统的Poyting-Thomson模型不仅可以能够很好地模拟岩石衰减蠕变及稳态蠕变[11]阶段,而且可以反映岩石瞬时弹性变形,但是却无法有效模拟岩石亚稳态蠕变阶段及加速蠕变阶段.
1.2 改进后的Poyting-Thomson模型
由于传统的Poyting-Thomson模型中的元件都是线性元件,这也决定了其无法模拟岩石蠕变的加速蠕变阶段,因此本文在原模型的基础上通过再构建一个非线性元件,使得改进后的Poyting-Thomson模型能够模拟岩石蠕变全阶段.
本文通过在徐卫亚等[12]提出的非线性元件的基础上进行改进后,提出了新的黏性元件,该元件如图3所示.
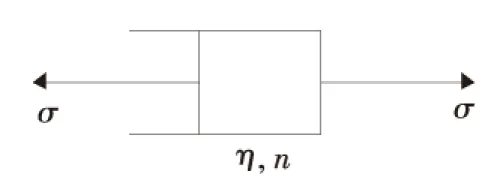
图3 本文所用的非线性流变元件示意图
改进后的黏性元件的应力-应变关系满足下式:
(3)

将改进后的非线性元件与Poyting-Thomson模型进行串联,得到四元件非线性黏弹塑性流变模型即改进的Poyting-Thomson模型,该力学模型如图4所示.

图4 本文构建的非线性黏弹塑性流变模型
1)当σ≤σs时,改进的四元件模型就相当于一个线性牛顿体黏壶与Poyting-Thomson模型串联,由此可得模型的状态方程为
(4)
2)当σ>σs时,本文建立的模型就变成一个非线性黏弹塑性流变模型,此时该模型的状态方程变为
(5)

通过对上述(4)、(5)式的整理,可以得出该模型的本构方程为
1)当σ≤σs时,模型本构方程为
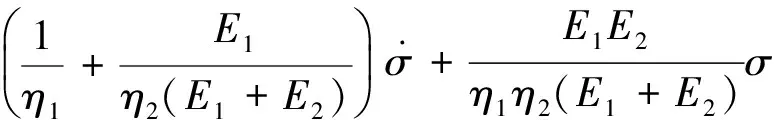
2)当σ>σs时,模型本构方程为


1.3 改进后的流变模型蠕变方程及其特性
当t=0时,σ=σ0,此时改进的四元件的流变模型需要满足以下初始条件:
(8)

将上述初始条件带入本构方程内,并利用Laplace变换可得到改进后的Poyting-Thomson模型的蠕变方程为
(10)

当σ0≤σs时,对应变分别求一阶导数与二阶导数可得
(12)

当σ0>σs时,分别对其求一阶导数与二阶导数可得
(14)


对改进后的Poyting-Thomson模型中的参数分别赋予合适的值,这里取E1=E2=10 MPa,η2=10 MPa·d,σ0=10 MPa,η1分别不同大小的的值,可以得到不同情况下的模型蠕变曲线.
当σ0≤σs时,改进的Poyting-Thomson模型的蠕变曲线如图5所示.

图5 改进的模型的蠕变曲线示意图
当σ0>σs时,E1=E2=10 MPa,σ0=10 MPa,η2=η2=10 MPa·d,n取不同大小的值,从而可以得到改进的Poyting-Thomson模型的蠕变曲线如图6所示.
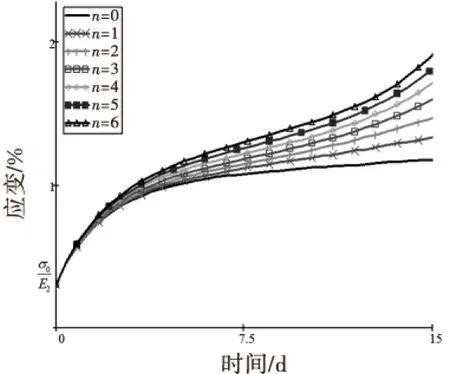
图6 不同n值下的模型蠕变曲线
根据图2、图5与图6中的蠕变曲线特点可知,当应力σ0>σs时,改进后的Poyting-Thomson模型不仅可以模拟稳态蠕变阶段,而且可以模拟亚稳态蠕变阶段,当σ0>σs时,通过对模型中的参数赋予不同的值,新模型可以模拟岩石的不同性态的蠕变全过程.
2 模型参数的确定
2.1 模型参数辨识方法
本文建立的四元件模型中共有5参数,所以参数的确定与其他模型参数确定相比具有很大的优势,这5个参数分别为;η1,n,E1,E2,η2,当σ0≤σs时,此时流变模型中只有η,E1,E2,η24个参数,利用试验曲线结合最小二乘法可以准确地确定这4个参数,当σ0>σs时,由于式中含有t的幂函数,为了得到更加精确的参数值,不宜再用最小二乘法,而是采用流变曲线分解法,即通过分析试验曲线中的应变率的变换特点,从而可以得出稳定蠕变与加速蠕变的临界时间tc,在tc之前利用最小二乘法拟合得到η,E1,E2,η24个参数,然后利用这4个参数得到岩石蠕变全程曲线,然后将试验曲线与得到的全程模拟曲线进行做差可以得到相应的差值,该差值为时间的函数,将该差值对时间t进行幂函数形式的拟合,从而可以得到流变指数n,至此,流变模型中的所有参数全部得出.
2.2 四元件非线性黏弹塑性模型参数辨识
本文通过引用邱贤德等[13]人的长山岩蠕变试验数据曲线以及邓荣贵等[14]人的岩石蠕变数据来进行验证模型的可靠性与正确性.初始应力为14.72 MPa条件下的长山岩单轴压缩蠕变试验曲线如图7所示.

图7 岩石蠕变试验曲线
为了检验本文所改进的Poyting-Thomson模型的正确性及可靠性,这里拟用经典的Burgers模型,未改进的Poyting-Thomson模型,以及改进的Poyting-Thomson模型分别对图7中的长山岩蠕变曲线进行拟合,拟合结果如图8所示.

图8 岩石试验数据及模型拟合曲线
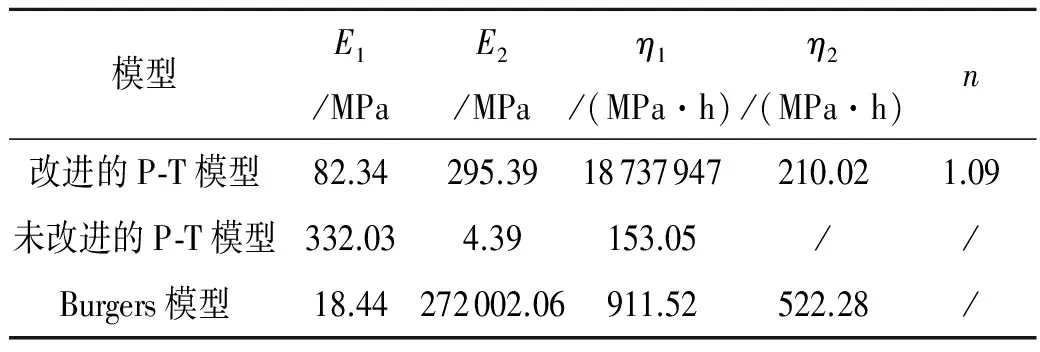
模型E1/MPaE2/MPaη1/(MPa·h)η2/(MPa·h)n改进的P⁃T模型82.34295.3918737947210.021.09未改进的P⁃T模型332.034.39153.05//Burgers模型18.44272002.06911.52522.28/
本文这里还对邓荣贵等人的岩石蠕变试验曲线进行拟合,该试验是在单轴压力为0.7 MPa下的岩石蠕变试验,其岩石蠕变数据如图9所示.

图9 岩石蠕变试验曲线
这里仍用上述3种模型对蠕变试验数据进行拟合,模型拟合结果如图10所示.

图10 岩石试验数据及模型拟合曲线

模型E1/MPaE2/MPaη1/(MPa·h)η2/(MPa·h)n改进的P⁃T模型26.5271.08771483.864908.090.42未改进的P⁃T模型88.191.9468.06//Burgers模型363.1452317.63673.7197.28/
通过图8与图10中模型的拟合曲线可知,改进后的Poyting-Thomson流变模型较未改进的Poyting-Thomson流变模型以及经典的Burgers模型对岩石的蠕变数据拟合程度更好,这表明改进后的Poyting-Thomson模型的正确性及可靠性.
3 结 论
1)本文通过在Poyting-Thomson流变模型的基础上引进非线性流变元件,建立新的四元件形式的非线性黏弹塑性流变模型,并推导了对应的本构方程及蠕变方程,并且对其流变特性进行了深入的探究,从中得出该模型具有以下特点:当σ0≤σs时,该模型能够较好地描述岩石蠕变的衰减阶段及稳定阶段,当σ0>σs时,该模型能够较好地模拟岩石蠕变全过程.
2)将本文建立的模型、传统的Poyting-Thomson流变模型以及经典Burgers模型分别对与长山岩与水电站坝区断层岩石蠕变试验曲线进行拟合.根据拟合结果可知,改进后的Poyting-Thomson模型对岩石的蠕变数据拟合程度更高,这表明了本文建立的改进后的Poyting-Thomson模型的正确性.
[1] 康永刚,张秀娥.一种改进的岩石蠕变本构模型[J].岩土力学,2014,35(4):1049-1055.
[2] 周家文,徐卫亚,杨圣奇.改进的广义Bingham岩石蠕变模型[J].水利学报,2006,34(7):827-830.
[3] 殷德顺,任俊娟,和成亮,等.一种新的岩土流变模型元件[J].岩石力学与工程学报,2007,26(9):1899-1903.
[4] 李成波,李建新,施行觉.高温下砂岩稳态蠕变规律的实验研究[J].科学技术与工程,2015,26(15):201-205.
[5] 朱昌星,阮怀宁,朱珍德,等.岩石非线性蠕变损伤模型的研究[J].岩土工程学报,2008,30(10):1510-1513.
[6] 徐卫亚,杨圣奇,褚卫江.岩石非线性黏弹塑性流变模型(河海模型)及其应用[J].岩石力学与工程学报,2006,25(3):433-447.
[7] 宋勇军,雷胜友.基于分数阶微积分的岩石非线性蠕变损伤力学模型[J].地下空间与工程学报,2013,9(1):91-95.
[8] 曹 平,刘业科,蒲成志,等.一种改进的岩石黏弹塑性加速蠕变力学模型[J].中南大学学报(自然科学版),2011,42(1):142-146.
[9] 曹文贵,袁靖周,王江营,等.考虑加速蠕变的岩石蠕变过程损伤模拟方法[J].湖南大学学报(自然科学版),2013,40(2):15-20.
[10] 康永刚,张秀娥.基于Burgers模型的岩石非定常蠕变模型[J].岩土力学,2011(S1):424-427.
[11] 张治亮,徐卫亚,王如宾,等.含弱面砂岩非线性黏弹塑性流变模型研究[J].岩石力学与工程学报,2011,30(S1):2634-2639.
[12] 徐卫亚,杨圣奇,谢守益,等.绿片岩三轴流变力学特性的研究(II):模型分析[J].岩土力学,2005,26(5):693-698.
[13] 邱贤德,姜永东,阎宗岭,等.岩盐的蠕变损伤破坏分析[J].重庆大学学报(自然科学版),2003,26(5):106-109.
[14] 邓荣贵,周德培,张倬元,等.一种新的岩石流变模型[J].岩石力学与工程学报,2001,20(6):780-784.

