基于ESO的BTT飞行器多变量解耦控制方法研究

杜立夫，张 瑞，赵志芳，闵 勇

(北京航天自动控制研究所，北京 100854)

0 引言

倾斜转弯(BTT)飞行器采用高升阻比的面对称气动外形,能产生高升力、大过载，在机动性、稳定性、升阻比特性和冲压发动机进气口设计的兼容性等方面，相比侧滑转弯(STT)飞行器有显著的性能优势[1-2], 受到国内外相关研制单位的高度重视,且发展迅速。

BTT飞行器的机动过程是：利用滚动通道快速将飞行器最大升力面滚转到所要求的机动方向;利用俯仰通道控制飞行器，使其在最大升力面内产生相应的攻角,获取需要的过载；利用偏航通道严格控制侧滑角，协调控制俯仰通道和滚转通道的运动，使侧向过载和侧滑角近似为零。故BTT飞行器的滚动角速率和滚动角度比STT飞行器大很多。另外，侧向风引起的斜吹力矩和不确定性因素会产生相应的瞬间侧滑角，致使飞行器俯仰通道、偏航通道和滚转通道之间严重耦合,从而使飞行器系统成为一个强耦合、复杂的多变量系统[3]。传统的三通道独立控制设计已不再适用于BTT飞行器,控制系统设计时须考虑运动学耦合、惯性耦合、气动耦合和控制作用耦合等多自由度耦合问题。

随着控制理论与应用的不断发展，越来越多的先进控制技术(如鲁棒控制、滑模控制、非线性动态逆控制等)被应用到BTT飞行器的解耦控制中。文献[4]中建立BTT导弹线性变参数模型,将耦合视为扰动，运用最小灵敏度特征值配置的鲁棒方法完成控制器设计，但控制方法较为繁琐，不易实现；文献[5]中运用变结构控制方法完成BTT导弹解耦控制，展示出良好的控制效果，但控制量具有抖动，需要进一步解决；文献[6]中运用非线性动态逆设计解耦控制器，解决了BTT飞行器的耦合问题和快速跟踪问题，动态逆方法是一种有效的非线性控制方法，但非线性动态逆在设计过程中对模型不确定性较敏感，需要增加系统的鲁棒性。

自中科院韩京清研究员提出自抗扰控制技术[7](ADRC)以来，该技术在理论和工程上取得了巨大的成果[8-9]。这得益于自抗扰控制技术中核心部分——扩张状态观测器(ESO)的引入，它可将系统的不确定性、未建模动态和外部扰动等视为“总和扰动”，并将其扩张成系统变量，然后设计状态观测器以实现对扰动的估计, 将其输出补偿到控制系统中，从而提高系统的性能。ESO不需要精确的模型信息，结构简单，易于实现，故其通用性较高，并在理论和工程实践中得到不断的发展和应用[10-12]。

通常，解决多变量耦合控制方法有两种。一种是将耦合视为扰动，通过设计增加控制器的鲁棒性来抑制耦合扰动的影响，增加了控制器的复杂程度，增大了控制器的负担，耦合大时解耦效果会受到一定的影响；另一种是建立耦合量的先验模型，通过补偿方法完成解耦控制[13]，模型的精确度会影响解耦控制的效果。为此，本文提出一种基于ESO的BTT飞行器多变量解耦控制方法，用反馈机制建立能观测耦合扰动作用的扩张状态观测器，该扩张状态观测器并不依赖生成耦合扰动的具体数学模型，也无须直接测量其作用，利用已知三通道独立设计控制器模型即可完成扩张状态的观测，不需要其他模型量即可实现对耦合扰动的估计与补偿，进一步设计独立三通极点配置的闭环反馈控制器，完成多变量的解耦控制，是一种通用、实用、便于工程实现的方法。

1 数学模型的建立

(1)

式中：α为攻角；β为侧滑角；γv为速度倾侧角；δx为滚动舵偏角；ωz为俯仰角速度；ωy为偏航角速度；ωx为滚转动角速度；δy为偏航舵偏角；δz为俯仰舵偏角；C、B为动力学方程系数，下角标f,p,g分别表示俯仰通道、偏航通道和滚转通道。显然，BTT飞行器数学模型是一个多变量耦合系统。

2 基于ESO的多变量解耦控制

将式(1)中的全部耦合项去掉，并将耦合项视为扰动，利用已知独立三通道模型设计ESO，观测耦合扰动，通过补偿方法进行解耦，进一步设计稳定的、独立三通极点配置的闭环反馈控制器，完成基于ESO的多变量解耦控制。

2.1 ESO的设计介绍

ESO是自抗扰控制技术[7]的重要组成部分，它可较为精确地估计出系统当前的不确定性，将这种不确定性补偿到控制系统中，从而增加系统的抗干扰能力。下面将阐述ESO的设计过程。

以2阶系统为例，多变量线性系统模型可表示为

(2)

式中：F(x1,x2)和G(x1,x2)为系统关于x1和x2的非线性函数向量模型，x1∈Rn、x2∈Rn均为系统状态向量，u∈Rm为控制输入向量。假设系统的一部分模型已知，把这个模型称作名义模型，则式(2)可改写为

(3)

式中：F0(x1,x2)、G0(x1,x2)为名义模型，而Fu(x1,x2)、Gu(x1,x2)为未知模型。则需要扩张的状态向量可表示为

d=Fu(x1,x2)+Gu(x1,x2)u

(4)

根据式(3)和式(4)，ESO设计式为

(5)

式中：向量z1为对系统向量x1的估计；向量z2为对系统向量x2的估计；z3为对不确定性向量d的估计；β01、β02、β03为ESO设计参数，使其均大于零即可保证扩张状态观测器稳定收敛[7]；f(e,κ,δ)为原点附近线性、连续的幂次函数，即

(6)

式中：e为ESO的偏差输入；δ为线性区间长度，一般取较小的数；κ为幂次函数的幂，一般取0.5。

由式(5)可知，把名义模型放入扩张状态观测器中，可得

(7)

此时被扩张的状态变量d的估计值z3(t)估计的就是作用于系统的不确定性部分，即ESO实时估计扰动功能，将这种扰动估计加以补偿实质就是抗干扰。

扩张状态观测是一个动态过程，观测器的结构示意图如图1所示。

图1 ESO结构示意图Fig.1 ESO structural schematic diagram

2.2 ESO的多变量解耦控制器设计

将BTT飞行器全量模型式(1)，去掉所有耦合项作为三通道独立设计的名义模型，其状态方程可表示为

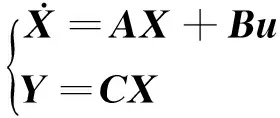
(8)

式中：状态变量X=[x1x2x3x4x5x6]T=[αβγvωzωyωx]T；控制变量u=[δxδyδz]T；输出变量Y=[αβγv]T。状态矩阵

(9)

(10)

输出矩阵C=[I3×303×3]。

把式(8)模型作为名义模型，进行ESO设计，完成状态和扰动估计，根据2.1节ESO设计介绍，ESO设计如下

(11)

(12)

式中：u0为闭环反馈控制律。

2.3 ESO的极点配置闭环反馈控制器设计

系统的性能和稳定性主要是由系统的特征根决定，即系统的极点。极点配置的状态反馈控制方法可使系统获得更优异的性能，下文运用极点配置的方法设计独立三通道控制器，完成闭环反馈控制。

由式(8)设计闭环状态反馈控制律，表达式为

u0=KX

(13)

式中：K为状态反馈控制参数向量。

将控制律具体形式展开，即

(14)

式中：kf1,kf2为俯仰通道反馈控制参数；kp1,kp2为偏航通道反馈控制参数；kg1,kg2为滚转通道反馈控制参数。

对三通道独立系统进行极点配置，俯仰通道、偏航通道和滚转通道的期望极点分别是-3±4j、-4±6j和-2±6j，由控制理论可知，系统中的特征根均分布在左半平面内，故可保证系统稳定[14]。通过MATLAB中极点配置函数K=place(A,B,p),即可得到三通道反馈控制参数向量K。

初始偏差Δα0=1°，Δβ0=1°，Δγv0=1°时的独立三通道系统的零输入响应，如图2所示,可以看出，独立三通道系统稳定，且参数很快收敛。图3为ESO的BTT飞行器解耦控制系统框图。

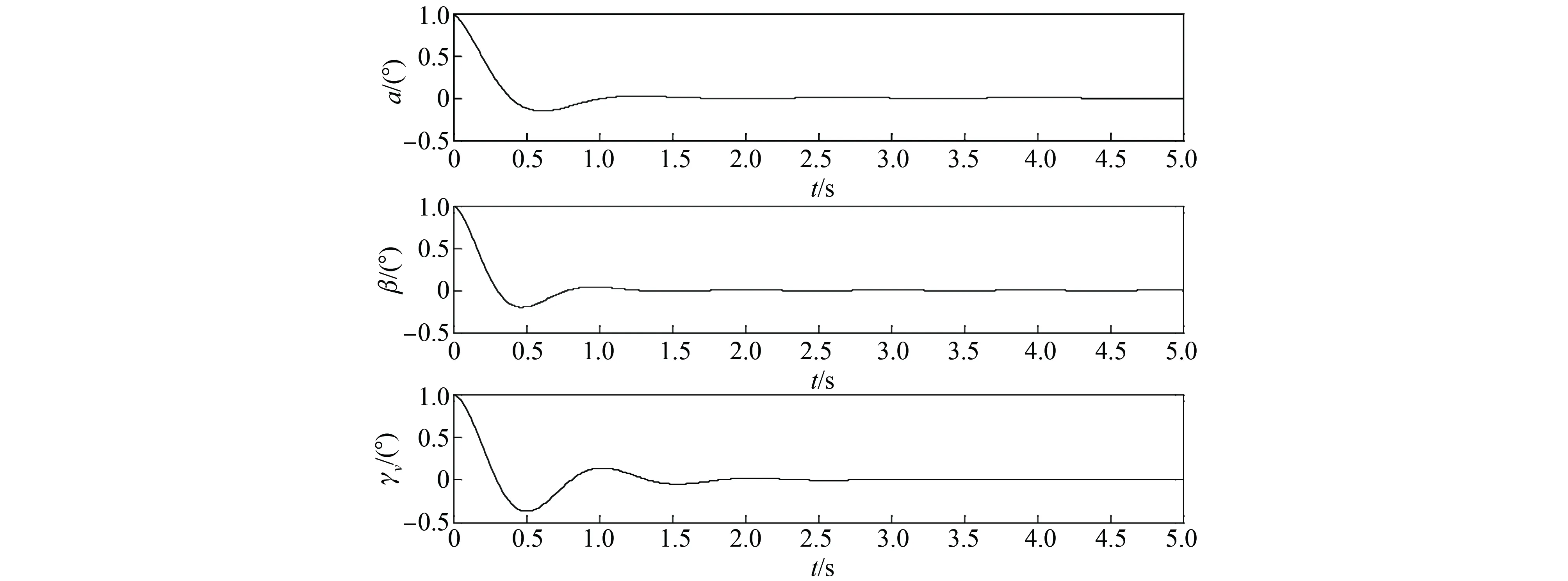
图2 独立三通道状态的零输入响应曲线Fig.2 Zero input response curve of the independent three-channel state

图3 基于ESO的BTT飞行器解耦控制系统框图Fig.3 Block diagram of decoupling control system for BTT aircraft based on ESO

3 仿真校验

基于MATLAB仿真分析BTT飞行器多变量耦合控制器，验证系统的解耦特性和控制系统性能。

3.1 仿真参数

选取BTT飞行器空域中的某特征点，其中飞行器质量、特征面积、特征长度、转动惯量参数均为已知，则飞行器的模型参数均为已知参数。

根据BTT飞行器控制要求，攻角初值取α0=0°,控制目标αcx=5°；侧滑角初值取β0=1°,控制目标βcx=0°；倾侧角初值取γv0=0°,控制目标γvcx=5°。

ESO参数设计如下

(15)

极点配置的三通道反馈控制参数如下

(16)

3.2 仿真结果

仿真周期为10 s，分别对极点配置方法设计的三通道独立控制器和ESO解耦控制器进行仿真对比，指令跟踪结果如图4～6所示。ESO对三通道耦合干扰的估计曲线如图7～9所示。

图4 攻角跟踪曲线Fig.4 Attack angle tracking curve

图5 侧滑角跟踪曲线Fig.5 Sideslip angle tracking curve

图6 倾侧角跟踪曲线Fig.6 Heeling angle tracking curve

图7 俯仰通道的ESO耦合干扰估计曲线Fig.7 ESO coupling interference estimation curve of pitching channel

图8 偏航通道的ESO耦合干扰估计曲线Fig.8 ESO coupling interference estimation curve of yaw channel

图9 滚转通道的ESO耦合干扰估计曲线Fig.9 ESO coupling interference estimation curve of rolling channel

3.3 仿真结果分析

1) 控制性能分析

图4～图6分别为攻角、侧滑角和倾侧角的跟踪曲线，当初始侧滑角不为零时，ESO解耦控制方法可使三通道输出平稳、快速、较小的超调跟踪指令信号。通过两种方法对比曲线可以看出，三通道独立控制方法跟踪性能较差，充分体现出ESO解耦控制方法的性能优势。

2) 解耦性分析

通过图4～图6可看出，三通道独立控制中偏航通道和滚转通道交连耦合严重，偏航通道的侧滑角最大值约0.5°，超调约40%；滚转通道最大值约11°，超调大于100%；俯仰通道受耦合影响较小。加入ESO解耦控制，耦合补偿可大大降低耦合影响，俯仰通道最大值有所降低；偏航通道最大值约为0.02°，超调小于2%；滚转通道不受超调影响。由此说明该方法可有效实现解耦控制。

3) ESO的观测性能分析

图7～图9分别为ESO对三通道耦合干扰的估计曲线，由图可知，ESO可较为精确地估计出耦合项干扰信号值，干扰信号值随耦合项值的变化而实时改变，这得益于ESO这种精准的耦合干扰跟踪。补偿可减少耦合影响，达到解耦的目的。此外，ESO参数取值大即提高观测器的带宽，可提高一定观测精度，但观测器带宽的增加会引入高频噪声，严重影响系统性能，故ESO参数即β01、β02取值要折中考虑。

通过控制设计和仿真分析，本文解耦控制方法由两部分组成，一个是极点配置的状态反馈控制，它主要影响系统的动态性能和稳定性；另一个是基于ESO的补偿控制，它对耦合进行估计和补偿，主要影响系统的解耦性能，当两个控制方法协调匹配时控制效果最佳。从上述分析可知，本文设计验证了基于ESO的多变量控制方法的正确性和有效性。

4 结束语

本文研究了基于ESO的BTT飞行器姿态控制系统的多变量解耦控制问题。BTT飞行器中侧滑角不为零，飞行器控制系统三通道交连耦合严重。为解决此问题，用反馈机制建立能观测耦合扰动作用的ESO，而它不依赖生成耦合扰动的具体数学模型，也无须直接测量其作用；利用已知设计控制器模型参数即可设计出扩张状态观测器，而不需要其他模型量。实现对耦合扰动的估计并对其进行补偿，进一步设计独立三通极点配置的闭环反馈控制器，完成多变量的解耦控制，是一种通用而实用的有效方法。通过数学仿真验证了所设计的多变量解耦控制方法的正确性和有效性，为BTT飞行器多变量解耦控制提供一种新思路，此方法可用于解决飞机、航天飞机、BTT导弹及高超声速飞行器等面对称的耦合姿态控制问题，具有一定的工程实用价值。此方法未考虑参数摄动的鲁棒性问题和参数变化的快时变问题，以及量测噪声的影响，后续将进一步研究和讨论。

[1] 叶振信, 傅维贤, 王万军, 等. 战术导弹BTT控制技术发展综述[J]. 航天控制, 2009, 27(5): 106-110.

[2] 张靖男, 赵兴锋, 郑志强. BTT导弹的发展现状与趋势[J]. 飞航导弹, 2006(10): 37-39.

[3] 王凌艳, 吕鸣, 孙未蒙, 等. BTT导弹的解耦问题综述[J]. 飞航导弹, 2009(6): 60-64.

[4] LEE C H, CHUNG M J. Gain scheduled state feedback control design technique for flight vehicles[J]. IEEE Transactions on Aerospace and Electronic Systems, 2001, 37(1): 173-182.

[5] 童春霞, 王正杰, 张天桥. BTT导弹的变结构解耦控制系统设计[J]. 宇航学报, 2006, 27(1): 27-30.

[6] 张艳, 段朝阳, 张平, 等. 基于动态逆的BTT导弹自动驾驶仪设计[J]. 北京航空航天大学学报, 2007, 33(4): 422-426.

[7] 韩京清. 自抗扰控制技术[M]. 北京: 国防工业出版社, 2009.

[8] CASTANEDA L A, LUVIANO-JUAREZ A, CHAIREZ I. Robust trajectory tracking of a Delta robot through adaptive active disturbance rejection control[J]. IEEE Transactions on Control Systems Technology, 2015, 23(4): 1387-1398.

[9] ZHENG Q, GAO L Q, GAO Z Q. On stability analysis of active disturbance rejection control for nonlinear time-varying plants with unknown dynamics[C]∥Proceedings of the 46th IEEE Conference on Decision and Control. New Orleans, LA, USA, 2007: 3501-3506.

[10] ZHU Z, XU D, LIU J, et al. Missile guidance law based on extended state observer[J]. IEEE Transactions on Industrial Electronics, 2013, 60(12): 5882-5891.

[11] GUO B Z, ZHAO Z L. On the convergence of an extended state observer for nonlinear systems with uncertainty[J]. Systems & Control Letters, 2011, 60(6): 420-430.

[12] ZHENG Q, GAO L Q, GAO Z Q. On validation of extended state observer through analysis and experimentation[J]. Journal of Dynamic Systems, Measurement, and Control, 2012, 134(2): 024505.

[13] 杜立夫, 黄万伟, 杨广慧, 等. 基于补偿方法的高超声速滑翔飞行器多变量输出解耦控制[J]. 航天控制, 2015, 33(4): 40-45.

[14] 胡寿松. 自动控制原理[M]. 北京: 科学出版社, 2008.