基于抛物线理论考虑多跨窜移时货运索道运行轨迹的研究

文曙东，杨 荣，景文川，马 青

(1．西南交通大学土木工程学院，四川 成都 610031；2. 北京青年政治学院计算机系，北京 100102;3. 四川电力送变电建设公司，四川 成都 610051)

架空绳索是索道设备的主要组成部分[1-2]。架空绳索力学是索道设计上不可缺少的基础知识。各国学者对悬索基础理论有不同研究：一种应用悬垂曲线理论研究，另一种应用抛物线理论研究[3-4]。前者在求悬索精确解方面取得成果，但解超越函数，在实际应用上存在一定困难。后者计算理论成熟，运算简单，在工程上被广泛应用。本文采用抛物线理论分析架空索道是建立在均匀重力场的作用下，对悬挂缆索做出一些基本假设。

a. 缆索为理想柔性的，既不能受压也不能受弯。因为索的界面尺寸与索长相比十分微小。因而界面的抗弯刚度在计算中可不考虑。索曲线有转折的地方，只要转折曲率半径不太小，局部弯曲也可不计。

b. 索的材料符合胡克定律，应力与应变符合线性关系。

c. 悬索的横截面面积及其自重在外荷载作用下的变化量十分微小，忽略不计。

d. 支撑架为刚性(即没有弹性压缩和弯曲变形)。

e. 缆索与索鞍之间可以滑动，并可在塔顶或锚碇处自由滑动或转动。

根据第e条，输变电工程中多跨索道各相邻跨悬索靠支架及鞍座承托，悬索在支点处可以窜移，主索悬挂在鞍座上，随着索道加载后受荷悬索拉力增大，鞍座发生偏摆，若鞍座两端拉力差大于此时悬索受到的最大静摩擦力，可导致悬索在不同跨之间窜移。此窜移量在计算索道货物运行轨迹时不能忽略，在计算某跨货物运行时索道的轨迹时，假定该跨前后m跨不考虑鞍座的摩擦力，悬索可以自由窜移，不考虑鞍座的偏摆情况下，本文分析各跨承载钢丝绳在货物通过的运行轨迹。另外，当悬空架设钢索的无荷中央挠度系数较小时，沿悬索曲线的均布荷重与沿弦线的均布荷重两者之间的误差是很微小的。此时，设悬索自重沿弦线均匀分布，即可导出以代数函数法表示的抛物线。在考虑多跨货运索道前后m跨悬索可以自由窜移后，利用抛物线假定，分析货物的运行轨迹对货运索道在运行中判断货物是否拖地，具有重要的现实意义。

1 悬索线型、曲线长和有荷挠度

无荷悬索的线型，取决于悬索的挠度(垂度)，挠度是衡量悬索张紧度和线型的尺度，一般以跨中垂度与跨度之比，即中挠系数S0来表征悬索的张紧程度。

悬索自重沿水平轴均布的线型任意点的挠度为

(1)

式中：l0为跨度；H0为水平分力；q0为悬索倾斜均布荷重换算成的水平均布荷重，即q0=w。

悬索曲线长度为

(2)

整理后:

(3)

(4)

2 多跨悬索平衡状态

当索道某跨悬索受到一个集中荷载作用，前后跨悬索都会向集中荷载处移动。离集中荷载越远的钢索窜移量越小，当窜移量小于一定数值后，窜移将对钢索线型和内力的计算基本不产生影响。而集中荷载前后发生显著窜移的跨数m可由试算或者根据已有工程经验给出。在实际工程中，可以试算多个m值，根据计算结果按最不利情况进行索道设计。

本文根据实际受力分析，认为各跨在窜移后承载绳水平分力相等，以此为条件，建立力的平衡方程，计算承载绳在鞍座处窜移对线型的影响。

多跨无荷悬索示意图如图1所示，其最大无荷拉力产生于最大跨上端支点，若是相同跨距，则产生最大倾角的上端支点。对于多跨索道，假定各跨在平衡状态下，悬索的水平分力相等，各跨中央挠度系数为

(5)

式中：l1、l2、l3分别为各跨斜距离；S01、S02、S03分别为各跨无荷中央挠度系数。

多跨悬索无荷拉力计算方法与单跨相同。

图1 多跨无荷悬索示意图

3 多跨悬索有荷状态下的平衡状态

货物在索道运行中，由于鞍座两端索力不平衡，会导致承重绳在鞍座上的窜移。本文假定货物在运行过程中，考虑各跨水平力相等，仅考虑m跨可以窜移，来计算窜移后的索道运行状态。

第1步：根据最大跨设定的无荷中挠系数，假定各跨水平力相等，计算各跨的无荷载线型，并计算出各跨的中挠系数，无应力长度。

第2步：考虑前后m跨内，计算荷载P作用在第i跨时，第i跨的水平力H，无应力长度。

第3步：考虑前后m跨内，非i跨，在水平力为H时，无荷载下的无应力长度。

第4步：考虑前后m跨可以窜移，窜移后各跨的无应力长度之和。

第5步：对比第1步相应跨的无应力长度之和，如果第4步计算出的无应力长度大于第1步的无应力长度，表示索道张紧程度偏松，应修正H+ΔH，否则修正为H-ΔH，ΔH为迭代步长。

第6步：修正第2步的第i跨在P作用下的水平力H，重复第2—5步，直到相应跨无应力长度相差小于一个很小的给定值为止。就得到考虑前后m跨窜移条件下各跨的状态。

4 算例

某送变电建设工地索道如图2所示，共3跨，其参数如下：

第1跨：跨度404 m，高差80.5 m

第2跨：跨度287 m，高差72.5 m

第3跨：跨度200 m，高差36.5 m

承载索数量：1 个

承载绳规格：1670 mmΦ19 mm

无荷中挠系数：0.033

吊具重量：1.00 kN

承载索荷载：21.55 kN

支架高度：10 m

图2 建设工地索道示意图

从左到右，对于跨长404 m的第1跨，该跨为该建设工地索道的计算跨。通过计算得到其无荷载下的线型、不考虑窜移集中荷载点轨迹、考虑1跨窜移和2跨窜移集中荷载点轨迹，如图3所示。

图3 第1跨线型(计算跨,横纵坐标比例1∶1)

同样，计算出其余两跨的线型如图4—图5所示。由于该建设工地索道总共为3跨，对于中间跨，考虑前后1跨窜移和考虑前后2跨窜移是相同的，故其计算的集中荷载点轨迹也相同。

通过计算，对于该建设工地索道各跨不考虑窜移、考虑前后1跨窜移、考虑前后2跨窜移的跨中挠度如表1所示。

图4 第2跨线型

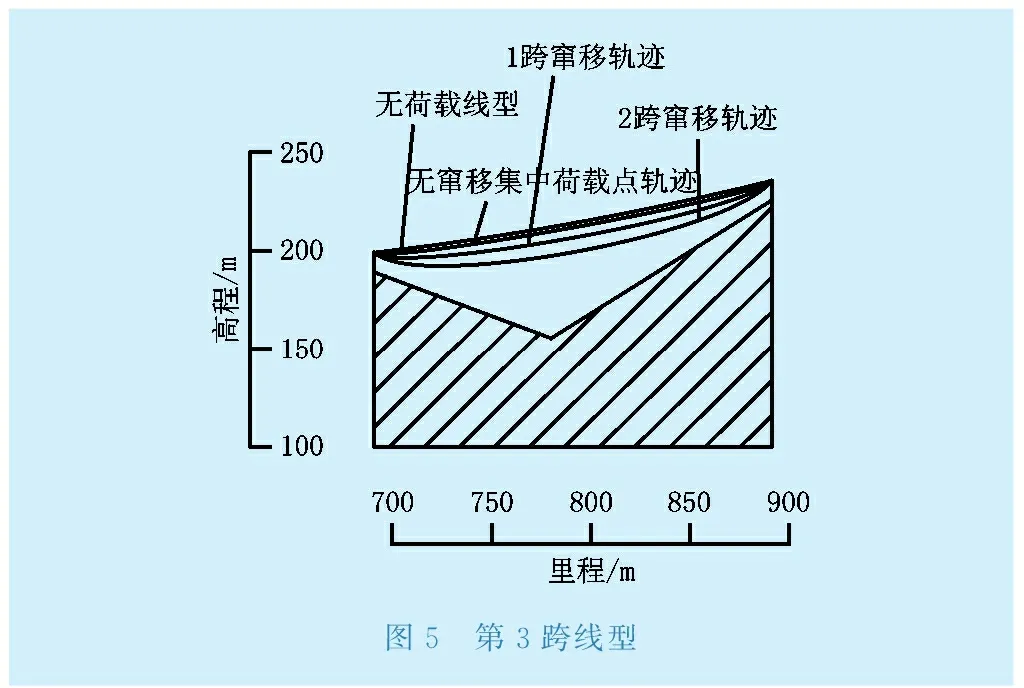
图5 第3跨线型

表1 各跨跨中挠度在不同窜移情况下的对比 m

5 结束语

当集中荷载作用在目标跨时，随着考虑窜移跨数的增加，目标跨的挠度有相应的增加。对于计算跨，其挠度增量的相对值不是很大，对于非计算跨，特别是跨度较小的跨，其挠度增量还是比较大的。不考虑鞍座的偏摆和鞍座的摩擦力，悬索可以自由窜移，所以本文计算的挠度值相对较大，偏保守。本文考虑目标跨前后特定数量跨度之间存在窜移，间接地考虑了鞍座的摩擦力。通过本文算例的比较，本文推荐在工程索道中采用考虑前后1跨窜移的计算方法。该方法简单，计算结果符合实际情况，又避免了考虑鞍座摩擦力的繁琐计算。

[1] 李志宏. 索道渡槽施工法的应用[J]. 东北电力技术，2005, 26 (5): 24-26.

[2] 张 雷.西藏昌都电网与四川电网联网输变电工程货运索道施工监理规范化管理[J]. 东北电力技术, 2016, 37(12):38-43.

[3] 加藤诚平. 林业架空索道设计法[M]. 北京: 农业出版社，1965: 48-183.

[4] 堀高夫 (日) . 悬索理论及其应用[M]. 北京: 中国林业出版社，1992:7-106.

[5] 冯建祥, 罗才英. 悬索工程[M]. 厦门：厦门大学出版社，2010:2-12.

[6] 官印生，周新年，郑丽风，等. 抛物线理论多跨索道设计模型[J]. 起重运输机械，2007(7): 12-17.