搅拌头转速对2024-T3铝合金搅拌摩擦焊接中晶粒生长的影响

，

(大连理工大学 1.工程力学系工业装备结构分析国家重点实验室；2.国际计算力学研究中心,大连 116024)

0 引 言

搅拌摩擦焊接(FSW)是一种利用高速旋转的搅拌探头与工件摩擦产生的热量使被焊材料局部塑化的新型固相焊接工艺，于1991年由英国焊接研究所发明，最初主要用于航空、航天工业铝及铝合金的焊接，现广泛应用于船舶制造工业、轨道交通及陆路交通工业等领域[1-2]。

搅拌摩擦焊接接头的显微组织及微观形貌主要取决于搅拌头的形状、搅拌头转速、焊接速度、轴肩压力和被焊材料的固有特性等因素。PAN等[3]采用光滑粒子法(SPH)模拟了镁合金的搅拌摩擦焊接过程，结合经验公式模拟出了镁合金在搅拌摩擦焊接过程中的晶粒变化。CHANG等[4]通过对AZ31镁合金搅拌摩擦焊接的试验研究，揭示了接头搅拌区晶粒尺寸与Zener-Hollomon参数的关系。张昭等[5]研究了搅拌针对搅拌摩擦焊接区晶粒尺寸的影响。张晓宁[6]在不考虑钉扎效应的条件下，运用蒙特卡洛法研究了钢在退火状态下晶粒的长大。CHO等[7]运用多晶体塑性和计算流体动力学模型来预测搅拌摩擦焊接区组织的演变。邹青峰等[8]研究了搅拌头形状对搅拌摩擦焊接接头显微组织和拉伸性能的影响。张昭等[9]采用有限元模拟研究了搅拌头尺寸对搅拌摩擦焊接材料流动及残余应力的影响。窦作勇等[10]采用X射线分析仪测定了铝合金搅拌摩擦焊接接头内部的残余应力。张昭等[11]基于ABAQUS计算平台研究了搅拌头转速对搅拌摩擦焊接区晶粒尺寸的影响。

在现有的试验研究中主要借助光学显微镜和扫描电子显微镜来观察材料的显微组织，也有基于动态再结晶经验公式来预测搅拌摩擦焊接区域的晶粒尺寸，但是目前国内外有关晶体生长过程模拟的研究还很少，而且大多为二维模拟，因此有必要建立数字化的、易于观测的搅拌摩擦焊接区域三维显微组织结构的计算模型。为此，作者基于2024-T3铝合金搅拌摩擦焊接的三维流体网格模型，将三维蒙特卡洛方法应用于焊核区的晶粒生长过程，模拟了不同搅拌头转速下焊核区晶粒尺寸的变化，并与相同焊接条件下的试验值进行对比。

1 计算模型

焊接试样为2个尺寸均为160 mm×37.5 mm×3 mm的2024-T3铝合金板。设定搅拌摩擦焊设备的轴肩直径为12 mm，搅拌头直径为4 mm，搅拌头的长度为2.4 mm，压入焊接试件表面的深度为0.3 mm，利用fluent软件的前处理器gambit建立模型，如图1所示。在流体力学模型中，搅拌头通常简化为流动边界条件，其接触区域的流动速度等效为搅拌头转速。采用分块网格划分法将搅拌区的网格细化，设定边界条件并导入fluent软件中进行计算。在计算时，取焊接构件中面p1、p2、p3、p4、p5等5个点的数据进行对比分析，其中p1点位于前进侧距焊缝2.1 mm处，p2点位于前进侧距焊缝1 mm处，p3点位于焊缝中心线，p4点位于后退侧距焊缝1 mm处，p5点位于后退侧距焊缝2.1 mm处。

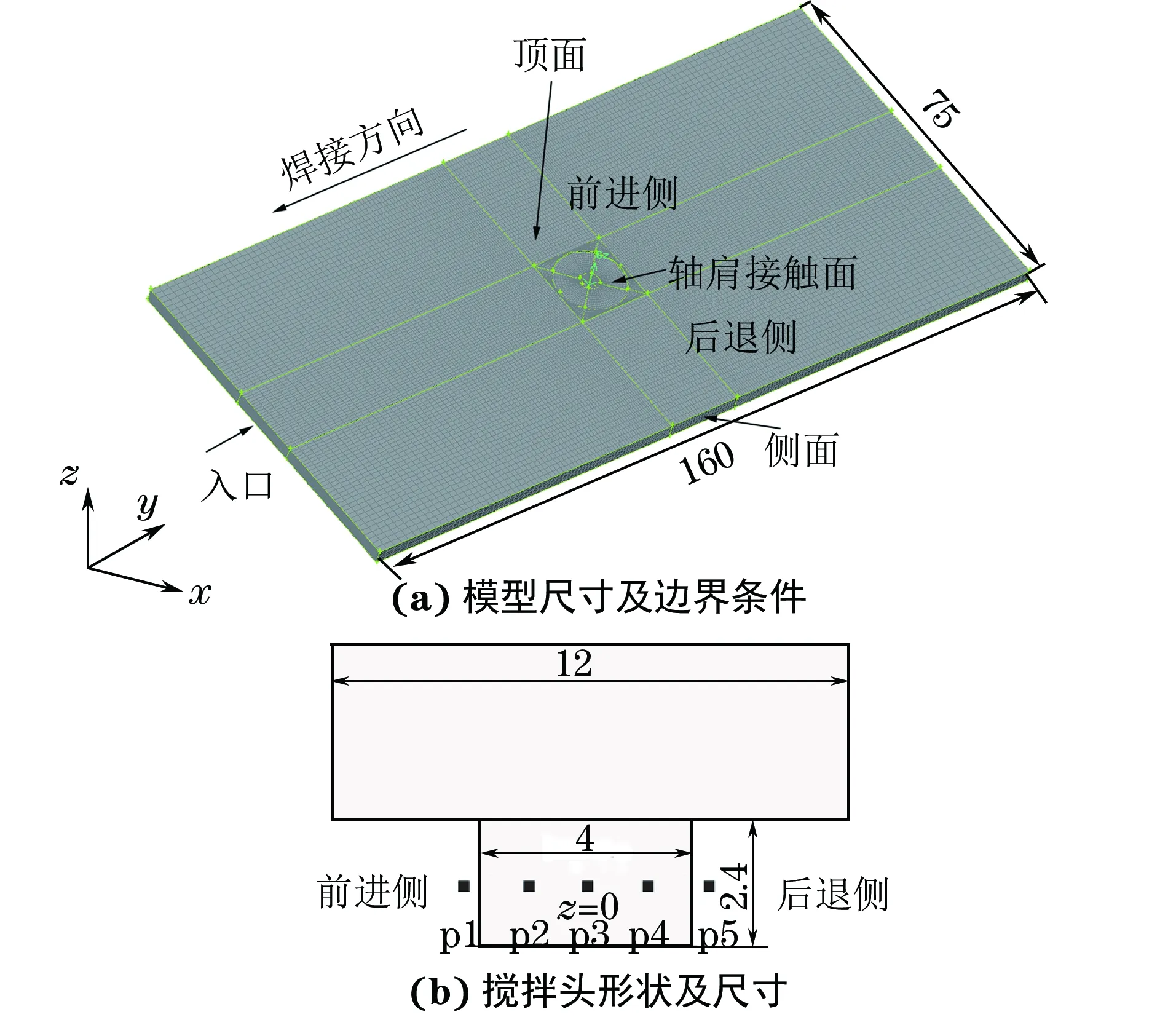
图1 搅拌摩擦焊接的计算模型Fig.1 Computing model of friction stir welding: (a) model size and boundary conditions and (b) shape and size of the stirring head

搅拌头的焊接速度为50 mm·min-1，搅拌头转速分别设置为400，600，800，1 000，1 200，1 500 r·min-1。中面处厚度坐标值z设为0。

在焊接过程中，轴肩和搅拌头底部所产生热量q0的计算公式[12]为

q0=β2[δτy+(1-δ)μfp0](ωr-Usinθ)

(1)

搅拌头侧面所产生热量q1的计算公式为

q1=β2[δτy+(1-δ)μfp0sinα](ωr-Usinθ)

(2)

式中：p0为轴肩和搅拌头底部的压力；μf为摩擦因数；τy为剪切屈服应力；δ为滑移率；β2为热转换效率；α为搅拌头的倾角；ω为搅拌头转速；U为焊接速度；θ为搅拌头轴线到任意点水平方向向量和焊接方向之间的夹角；r为摩擦接触点到搅拌头轴线的距离。

采用三维蒙特卡洛方法模拟焊接接头中的晶粒生长过程，该方法将需要模拟的焊核区离散成规则分布的点阵(N×N×N)，每个格点随机赋予1到Q的整数，用来代表该格点处晶粒的取向，在模拟中N取120，Q取30，对空间尺寸50 μm区域的晶粒生长过程进行模拟。若相邻格点的取向相同，则表示这两个格点处于一个晶粒内部；相邻格点的取向不同，则表示这两个格点处于晶界，晶界从两点之间穿过。晶界能的降低驱动着晶粒长大，晶界能由哈密顿函数[13]来描述，其函数为

(3)

采用逐步迭代方法模拟晶粒的生长过程，每一次蒙特卡洛迭代均在点阵中随机选取一个格点，将该格点的晶粒取向Si随机改为邻近取向(从邻近取向中随机选取)Sj，通过计算概率p来判断是否接受该改变，其计算公式为

(4)

式中：ΔE为改变前后的能量变化；k为玻尔兹曼常数；T为热力学温度;n2为改变前，与邻近取向不同的数目;n3为改变后，与邻近取向不同的数目。

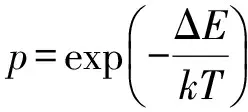
通过蒙特卡洛模拟，得到晶粒尺寸与蒙特卡洛步数(MMCS)之间的经验公式[15]

L=K1λ(MMCS)n1

(5)

式中：L为平均晶粒尺寸；λ为初始格点长度；K1为生长曲线的截距；n1为生长曲线的最大斜率。

边界迁移速度与晶粒尺寸变化速率呈正相关，假设其关系[14]为

(6)

式中：t为时间；v为边界迁移速度；α为比例常数，取1；n为比例常数，取0.49。

将蒙特卡洛模拟过程与搅拌摩擦焊接各区域晶粒生长过程相结合，建立蒙特卡洛步数与焊接区域的温度历程、晶粒生长过程和时间历程的关系。而实际晶粒的生长由晶粒边界的运动来驱动，其边界迁移速度[16]可表示为

(7)

式中：Vm为原子的摩尔体积，1.0×10-5m3·mol-1；Z为边界面平均原子个数，4.31×1020个·m-2；h为普朗克常数，6.624×10-34J·s；Na为阿伏伽德罗常数，6.02×1023mol-1；R为气体常数，8.31 J·K-1·mol-1；T为热力学温度；ΔSf为熔化熵，11.5 J·mol-1·K-1；Q为2024铝合金的激活能，148.88 kJ·mol-1；γ为边界能，0.5 J·m-2[12,17-20]。

联立式(5)～式(7)，得到蒙特卡洛步数与温度历程、时间历程的关系[14]。

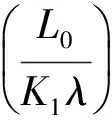
(8)

(9)

式中：Ti为每个时间段的平均温度；ti为时间段；L0为再结晶初始形核大小，在该模型中取0.49 μm；K1取1；n1取0.4；λ取0.42。

由式(8)可以看出，蒙特卡洛迭代步数的变化主要取决于时间和温度的变化。

在搅拌摩擦焊接过程中，搅拌头转速较高，焊核区母材被高速搅拌，从而发生塑性变形，并且由于焊核区与搅拌头直接接触，晶粒被破碎细化，导致该区域由搅拌所产生的塑性变形最为剧烈、热量最多，因此焊核区经历了类似动态回复再结晶的过程。

对铝合金的搅拌摩擦焊核区进行晶粒生长模拟，由图2可知，焊核区平均晶粒尺寸的对数值与蒙特卡洛步数的对数值呈线性关系，晶粒生长指数为0.45，与理论值0.5[13]非常接近，这验证了三维蒙特卡洛模型的有效性。

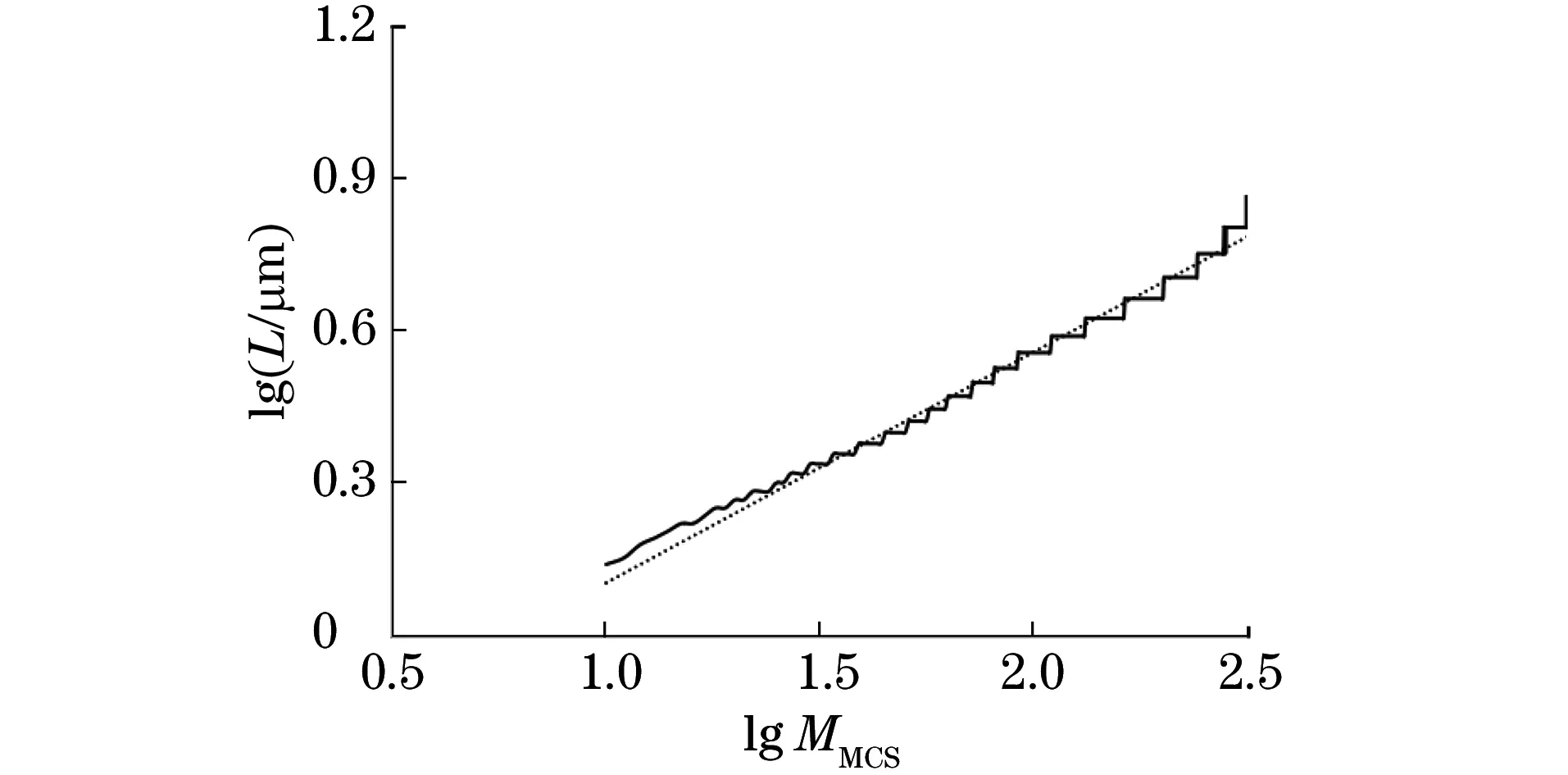
图2 焊核区蒙特卡洛步数与平均晶粒尺寸的关系Fig.2 Relationship between Monte-Carlo steps and the average grain size in stirring zone

2 计算结果与分析

由图3可知：随着搅拌头转速的增加，铝合金搅拌摩擦焊接温度升高；当搅拌头转速为400，600，800，1 000，1 200，1 500 r·min-1时，最高焊接温度分别为720，732，761，772，783，788 K。由图4可知，搅拌摩擦焊接中最高焊接温度随搅拌头转速的增加而升高，但当搅拌头转速较高时，继续增加搅拌头转速对最高焊接温度的影响减弱，这说明继续提高搅拌头转速并不能持续、有效地增加焊接温度，反而导致热效率下降。

由图5可知：随着搅拌头转速的增加，铝合金的流动速度随之增加，这是因为随着搅拌头转速的增加，焊核区温度升高，铝合金的黏度降低，焊核区的流动速度提高；当搅拌头转速为400，600，800，1 000，1 200，1 500 r·min-1时，铝合金的最高流动速度分别为120，170，220，260，320 mm·s-1；由速度场的流动速度方向可看出搅拌头附近铝合金的流动趋势。

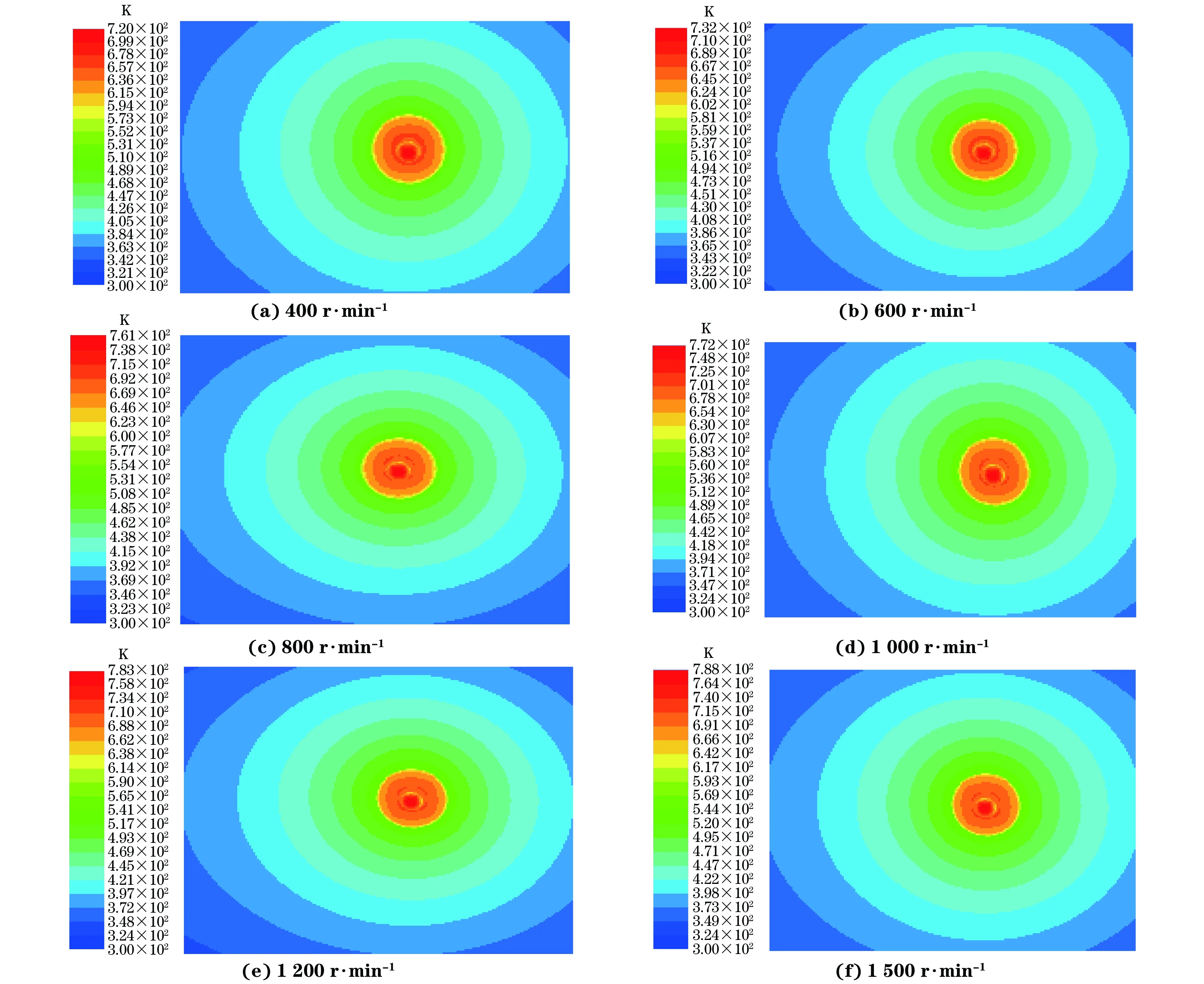
图3 不同搅拌头转速下焊核区的温度云图(z=1 mm)Fig.3 Temperature contours of the stirring zone at different rotating speeds of stirring head(z=1 mm)

图4 焊核区的搅拌头转速与最高焊接温度的关系曲线Fig.4 Rotation speed of stirring head vs peak welding temperature curve in stirred zone

铝合金的晶粒生长发生在焊接升温与焊后退火过程中，因此焊接温度历程显著影响其最终晶粒尺寸。将焊接后的铝合金数据导入到tecplot中进行处理，得到如图6所示的不同搅拌头转速下的中面流线图，其流线数据即为模拟截面的温度、时间历程。将温度历程代入式(8)，可以确定铝合金不同位置晶粒生长所对应的蒙特卡洛步数。

图7为搅拌摩擦焊接区域示意[21]，图中SZ为焊核区，TMAZ为热力影响区，HAZ为热影响区，BM为母材区。在搅拌头剧烈的旋转搅拌作用下，母材晶粒被破碎细化，生成细小致密的晶粒。在同一工况下提取多组焊核区的流线数据，提取点为图1(b)中的p1、p2、p3、p4、p5等5点，将温度、时间数据代入式(8)中得到对应的蒙特卡洛步数。由计算结果可知，焊核区前进侧晶粒尺寸略大于后退侧的。由图6可以看出，焊核区物质粒子的流动行为是不同的，搅拌头前进侧铝合金随着搅拌头转动而发生绕流。而由式(8)可知，温度历程是搅拌摩擦焊接晶粒生长中的一个重要影响因素,搅拌头前进侧铝合金明显比后退侧经历更长的高温时间，因此前进侧晶粒尺寸略大于后退侧的。由模拟晶体生长的蒙特卡洛步数所对应的晶粒尺寸计算结果得到蒙特卡洛模拟下的平均晶粒尺寸。

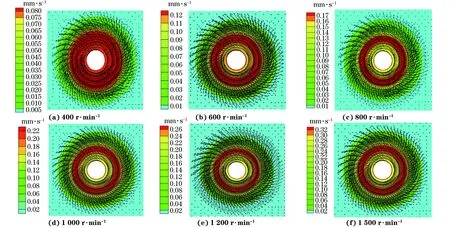
图5 不同搅拌头转速下焊核区的流动速度场(z=0)Fig.5 Velocity field of stirring zone at different rotation speeds of stirring head (z=0)

图6 不同搅拌头转速下的中面流线图(z=0)Fig.6 Streamlines of middle surface at different rotation speeds of stirring head (z=0)

图7 搅拌摩擦焊接区域示意Fig.7 Diagram of friction stir welding zone

图8 焊核区晶粒尺寸的试验值与预测值的对比Fig.8 Comparison of experimental and predicted grain size

在相同焊接条件下，将晶粒尺寸的试验值[21]与模拟预测值进行对比。由图8可以发现，焊核区晶粒尺寸的模拟预测值与试验值吻合良好，这说明三维蒙特卡洛模型可以很好地模拟不同搅拌头转速下焊核区的晶粒尺寸和晶粒生长过程。在式(8)中，α和n是在搅拌头转速为800 r·min-1时进行取值的，因此偏离该工况越远，计算误差越明显。

由于搅拌摩擦焊接焊核区大部分热量由搅拌头与铝合金间的摩擦而产生，随着与轴肩距离的增加，温度逐渐降低。当搅拌头转速为800 r·min-1时，计算得到焊核区中缝处上表面的平均晶粒尺寸为5.8 μm，略大于中面的5.3 μm和下表面的5.2 μm。CHANG等[4]、NORMAN等[22]也得到类似的结论，验证了蒙特卡洛模型的准确性。当搅拌头转速为800 r·min-1时，由焊核区中缝处上表面、中面、下表面的蒙特卡洛模拟结果得到其晶粒尺寸及分布，如图9所示。

当搅拌头转速为400，1 000，1 500 r·min-1时，得到焊核区中缝处中面的蒙特卡洛步数分别为139，263，352，平均晶粒尺寸分别为3.7，6.7，7.2 μm，平均晶粒尺寸随搅拌头转速的增加而增大。不同搅拌头转速下焊核区中缝处中面的晶粒生长过程如图10所示。

图9 搅拌头转速800 r·min-1时铝合金焊核区中缝处不同位置的晶粒分布Fig.9 Grain distributions at different positions of the center seam in the stirring zone at the rotation speed of stirring head of 800 r·min-1： (a) top surface; (b) middle surface and (c) bottom surface

图10 不同搅拌头转速时焊核区中缝处中面晶粒生长过程模拟示意Fig.10 Simulating diagrams of the grain growth process on the middle surface of the center seam in the stirring zone at different rotation speeds of stirring head

3 结 论

(1) 采用三维蒙特卡洛模型模拟2024-T3铝合金搅拌摩擦焊接焊核区晶粒生长过程，可以较好地反映不同搅拌头转速下的晶粒尺寸变化，焊核区平均晶粒尺寸的模拟预测值与相同焊接条件下的试验值吻合良好，实现了焊核区域晶粒组织的三维可视化。

(2) 焊核区平均晶粒尺寸随搅拌头转速的增加而增大；在相同焊接条件下，搅拌头前进侧铝合金随着搅拌头转动而发生绕流，相较于同一层面的后退侧经历更长的高温时间，导致搅拌头前进侧的晶粒尺寸略大于后退侧的；焊核区中缝处上表面的平均晶粒尺寸略大于中面的，下表面的平均晶粒尺寸最小。

[1] MISHRA R S, MA Z Y. Friction stir welding and processing [J]. Materials Science and Engineering R Reports, 2005, 50(1/2):1-78.

[2] NANDAN R, DEBROY T, BHADESHIA H K D H. Recent advances in friction-stir welding—Process, weldment structure and properties [J]. Progress Materials Science, 2008, 53(6):980-1023.

[3] PAN W X, LI D S, TARTAKOVSKY A M,etal. A new smoothed particle hydrodynamics non-Newtonian model for friction stir welding: Process modeling and simulation of microstructure evolution in a magnesium alloy [J]. International Journal of Plasticity, 2013, 48(3): 189-204.

[4] CHANG C I, LEE C J, HUANG J C. Relationship between grain size and Zener-Holloman parameter during friction stir processing in AZ31 Mg alloys [J]. Scripta Materialia, 2004, 51(6):509-514.

[5] 张昭, 吴奇. 搅拌针对搅拌摩擦焊接搅拌区晶粒影响研究[J]. 兵器材料科学与工程，2014, 37(5): 32-35.

[6] 张晓宁. 蒙特卡洛法模拟Ti-IF钢退火状态下的晶粒长大[J]. 金属热处理, 2015, 40(7):172-175.

[7] CHO H H, HONG S T, ROH J H,etal. Three-dimensional numerical and experimental investigation on friction stir welding processes of ferritic stainless steel [J]. Acta Materialia, 2013, 61(7):2649-2661.

[8] 邹青峰, 钱炜, 安丽, 等. 搅拌针形状对2A14铝合金搅拌摩擦焊接头组织和拉伸性能的影响[J]. 机械工程材料, 2015， 39(5):37-41.

[9] 张昭, 陈金涛, 张洪武. 搅拌头尺寸变化对搅拌摩擦焊接的影响[J]. 材料工程, 2006, 34(1): 19-23.

[10] 窦作勇, 张鹏程, 李云, 等. 铝合金搅拌摩擦焊接头内部残余应力的短波长X射线测试[J]. 机械工程材料, 2015, 39(3):107-110.

[11] 张昭, 吴奇, 张洪武. 转速对搅拌摩擦焊接搅拌区晶粒尺寸影响[J]. 材料工程, 2015, 43(7): 1-7.

[12] SU H, WU C S, PITTNER A,etal. Thermal energy generation and distribution in friction stir welding of aluminum alloys [J]. Energy, 2014, 77: 720-731.

[13] YANG Z, SISTA S, ELMER J W,etal. Three dimensional Monte Carlo simulation of grain growth during GTA welding of titanium [J]. Acta Materialia, 2000, 48(20): 4813-4825.

[14] 张昭, 吴奇, 万震宇, 等. 基于蒙特卡洛方法的搅拌摩擦焊接晶粒生长模拟[J]. 塑性工程学报, 2015，22(4): 172-177.

[15] SISTA S, YANG Z, DEBROY T. Three-dimensional Monte Carlo simulation of grain growth in the heat-affected zone of a 2.25Cr-1Mo steel weld [J]. Metallurgical and Materials Transaction B, 2000, 31(3): 529-536.

[16] GAO J H, THOMPSON R G. Real time-temperture models for Monte Carlo simulations of normal grain growth[J]. Acta Materialia, 1996, 44(11):4565-4570.

[17] DRIVER G W, JOHNSON K E. Interpretation of fusion and vaporisation entropies for various classes of substances, with a focus on salts [J]. Journal of Chemical Thermodynamics, 2014, 70:207-213.

[18] YANG C C, ROLLETT A D, MULLINS W W. Measuring relative grain boundary energies and mobilities in an aluminum foil from triple junction geometry [J]. Scripta Materialia, 2001, 44(12):2735-2740.

[19] KIRCH D M, JANNOT E, MORA L A B,etal. Inclination dependence of grain boundary energy and its impact on the faceting and kinetics of tilt grain boundaries in aluminum [J]. Acta Materialia, 2008, 56(18):4998-5011.

[20] 梅平, 甘光奉, 雷秀斌,等. 估算金属熔化热和熔化熵的经验公式[J]. 科学通报, 1989(8):80-80.

[21] KHODIR S A, SHIBAYANAGI T, NAKA M. Microstructure and mechanical properties of friction stir welded AA2024-T3 aluminum alloy [J]. Materials Transactions, 2006, 47(1): 185-193.

[22] NORMAN A F, BROUGH I, PRANGNELL P B. High resolution EBSD analysis of the grain structure in an AA2024 friction stir weld[C]//Materials Science Forum. Switzerland: Trans Tech Publications, 2000: 1713-1718.