基于改进诱导有序加权调和平均(IOWHA)算子的传染病组合预测模型研究

，

在我国，疾病导致死亡的因素中传染病占了很大的比重。而且传染病的危害也越来越严重，因此在分析研究传染病爆发规律的基础上，及时采取科学有效的方法对传染病的发病率及其发展规律进行预测，能够为制定有效的预防措施和控制传染病的发展提供科学的依据。随着人们对健康越来越重视，对传染病预测精度的要求也越高。然而传染病存在大量复杂的不确定影响因素，因此不容易获得高精度的预测结果。

目前，传染病预测方法很多，不同的预测模型具有不同的适应特征[1]。组合预测模型在提高精度方面比单个模型有明显的优势，因此如何选取恰当的单个模型和采取哪种组合形式将直接影响最终的预测精度。单一模型如ARIMA模型[2]、支持向量机[3]、灰色模型[4]、神经网络模型[5]等的应用最广泛。蔡海洋[6]构建了一种ARIMA- LSSVM组合预测模型，并将这两个模型的预测值采用LSSVM方法确定合适的权重，得出预测结果，预测值明显优于这两个单个模型；叶晓军[7]建立了基于GRNN的组合预测模型，通过GRNN模型将残差修正GM(1,1)和ARIMA季节模型拟合的肺结核月发病率赋予变化的权重系数进行组合预测，拟合结果理想；严薇荣[8]采用串联的方式建立了兼有ARIMA和GRNN模型优点的组合预测模型，神经网络因具有自学习和高度非线性逼近能力而被广泛用于预测；周玲玲[9]构建了混合ARIMA-NARNN模型预测人类血吸虫病的流行趋势，为检测和防控血吸虫病感染提供依据；吴文博[10]构建了遗传算法优化的ARIMA-BP组合预测模型对手足口传染病进行预测。

组合预测模型最核心的问题在于如何确定权重系数，使组合模型更高效地提高预测精度。组合方法有神经网络方法[7]、串联组合[8]、遗传算法[10]、非线性组合方法[11]、变权重组合方法[12]等。虽然上述组合预测模型在组合单个模型时，都提出了确定权重系数的行之有效的方法，但依然存在缺陷，不管是哪种组合方法赋予各单项模型的权重系数都只与第i种预测方法有关，而与时间t无关。实际上同一个单项模型在不同时刻的预测结果并不相同，在某一时刻预测精度高，在另一时刻可能低。为了克服组合预测模型赋权问题的缺陷，本文在诱导有序加权调和平均(IOWHA)算子[13]的基础上，将Theil不等系数与IOWHA算子[14]相结合，提出了一种改进IOWHA算子的SARIMA-GM相结合的组合预测模型。该模型是依据每个单项模型在各个时间点的预测精度的高低按顺序赋予权重，总体提高预测精度，同时通过实例应用证明了该方法的有效性。

1 基本理论

1.1 ARIMA季节模型

差分自回归移动平均模型(ARIMA)是一种专门针对非平稳复杂时间序列模式的预测方法，综合考虑了时间序列的周期变化、趋势特征，是时间序列预测中常用且精度又高的一种方法。ARIMA差分自回归移动平均模型记为ARIMA(p,q,d)，常用于医学领域[15]、计算机领域[16]及交通领域[17]。其中p和q表示时间序列的自回归阶数和移动平均阶数，d表示时间序列成为平稳序列所做的差分次数。若时间序列存在季节性周期波动，则采用乘积季节性差分自回归移动平均模型[18]，消除季节性差分，估计季节参数。ARIMA乘积季节模型记为ARIMA(p,d,q)(P,D,Q)，其中P、Q表示时间序列的季节自回归阶数和季节移动平均阶数，D表示时间序列成为平稳序列所做的季节差分次数。

ARIMA(p,d,q)(P,D,Q)模型记为：

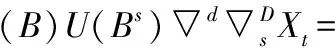
(1)

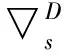
U(Bs)=1-Γ1Bs-Γ2B2s-…-ΓPBPs

(2)

V(Bs)=1-H1Bs-H2B2s-…-HQBQs

(3)

(4)

ARIMA模型的预测分为5个步骤。

数据的预处理：判断原始数据的平稳性，并将数据进行平稳性处理。

模型识别：判断时间序列服从的时序模型，根据其统计特征确定初步的模型结构，即判断模型和确定阶数p、q、d、P、Q、D的大小，通常采用AIC准则或BIC准则来确定选择参数。

模型估计：对识别的模型进行参数估计及确定，参数估计的方法有最小二乘法、极大似然法和矩向量估计。

模型检验：模型的显著性检验，即残差序列是否为白噪声序列，模型参数的显著性检验，即参数是否有效。

模型应用：参数确定后以及模型检验能够使用后，便可以用该模型对时间序列进行预测。预测流程如图1 所示。

1.2 灰色预测模型理论

GM(1,1)模型是灰色模型中最基础也是最常用的一种预测模型。因其建模过程简单、易于求解、预测效率好且精度高等特性而被广泛应用于各个领域的预测问题，如用电量预测[19]、建筑安全事故预测[20]和疾病预测[4]等。具体的建模过程如下：设原始序列X(0)为

X(0)=[X(0)(1),X(0)(2),…,X(0)(n)]

(5)

对X(0)做一次累加(1-AGO)，累加的目的是为了弱化随机序列的波动性和随机性，得到新的序列：

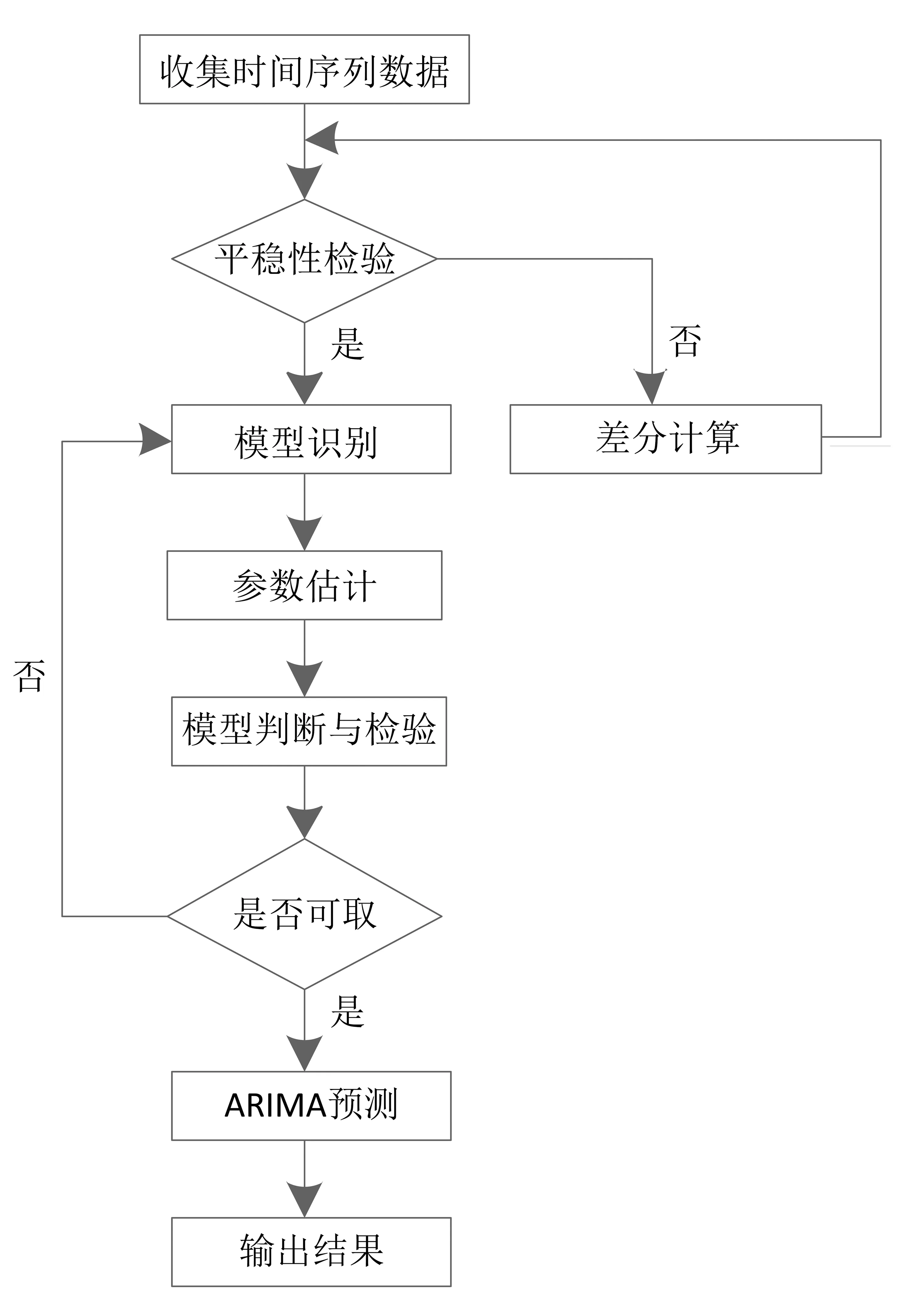
图1 ARIMA模型的预测流程

X(1)=[X(1)(1),X(1)(2),…,X(1)(n)]

(6)

对X(1)做邻均值生成等权数列：

Z(1)=[Z(1)(1),Z(1)(2),…,Z(1)(n)]

(7)

根据灰色理论建立灰色模型GM(1,1)的微分方程模型为：

x(0)(k)+az(1)(k)=b

(8)

式中，X(0)(k)称为灰导数；a为灰系数，表示X(0)的增长速度；b为灰作用量，表示序列X(0)的数据变化。对累加生成数据做均值生成B与常数项向量Y

(9)

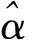
2 基于Theil不等系数的IOWHA算子组合预测模型

2.1 IOWHA算子和Theil不等系数

2.1.1 IOWHA算子

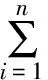
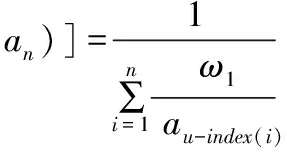
(10)

则函数fω被称为u1,u2,…,un所产生的n维诱导有序加权调和平均算子，简称为IOWHA算子。ui为ai的诱导值，u-index(i)是u1,u2,…,un中按从大到小的顺序排列的第i个大的数的下标。从公式中可以看出IOWHA算子是对诱导值u1,u2,…,un按从大到小的顺序排列后所对应的a1,a2,…,an进行有序加权调和平均。权系数ωi与ai的大小及位置无关，而与其相对应的诱导值所在的位置有关。

2.1.2 Theil不等系数

Theil不等系数是一种衡量模型预测精度的评价指标，其计算公式为：

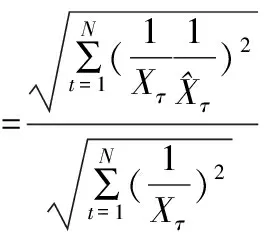
(11)

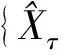
2.2 改进IOWHA算子的ARIMA-GM组合预测模型

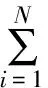
(12)

式中，ait表示第i种单项预测方法在第t时刻的预测精度，且ait。∈[0,1]。我们把预测精度看作是预测值的诱导值，从而得到组合模型中n种单项预测方法在第t时刻的预测精度与其在样本区间的预测值构成了n个二维数组(a1t,X1t)，(a2t,X2t),…，(ant,Xnt)。设a-index(it)表示n种单项预测方法在第t时刻的预测精度序列按从大到小的顺序排列后的第i个大的数的下标，则n种单项预测模型在第t时刻的预测精度序列的IOWHA组合预测值公式如下：

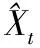
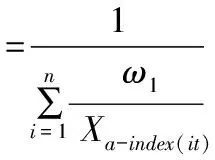
(13)

从式中看出，组合预测模型的权重系数与单项预测方法类别无关，而与各个单项预测方法在各个时刻点的预测精度大小密切相关。

结合上式(13)令

式中，et表示组合预测值在第t时刻与实际值之间的倒数误差，i=1,2,...,n，t=1,2,...,N。

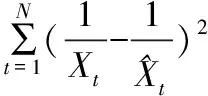
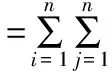
(15)

式中，F=(Fij)n×n表示n阶IOWHA算子的组合预测协方差信息方阵。所以基于IOWHA算子的组合预测值倒数序列与实际值倒数序列的Theil不等系数τ可表示为：

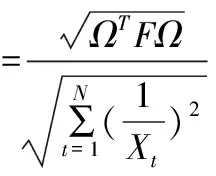
(16)

上式表明基于Theil不等系数的IOWHA算子组合预测值序列与实际观察值序列的Theil不等系数为组合预测方法的权重系数ω1,ω2,…,ωn的函数，τ(ω1,ω2,…,ωn)，τ(ω1,ω2,…,ωn)越小，则组合预测模型的精度就越高。所以基于Theil不等系数的IOWHA算子组合预测模型表达式如下：

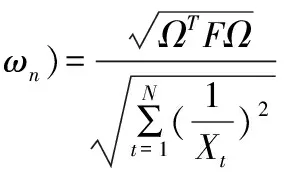
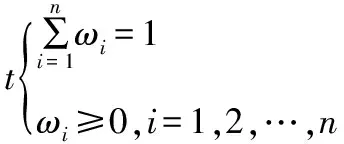
(17)

该模型实际上是一个线性规划问题，可用MATLAB进行求解。只有当τ(ω1,ω2,…,ωn)<τmin，该组合预测模型的结果才是优性的，其中τmin表示n种单项预测倒数值序列与实际值倒数序列的Theil不等系数的最小值。

组合预测模型的基本步骤如图2所示。

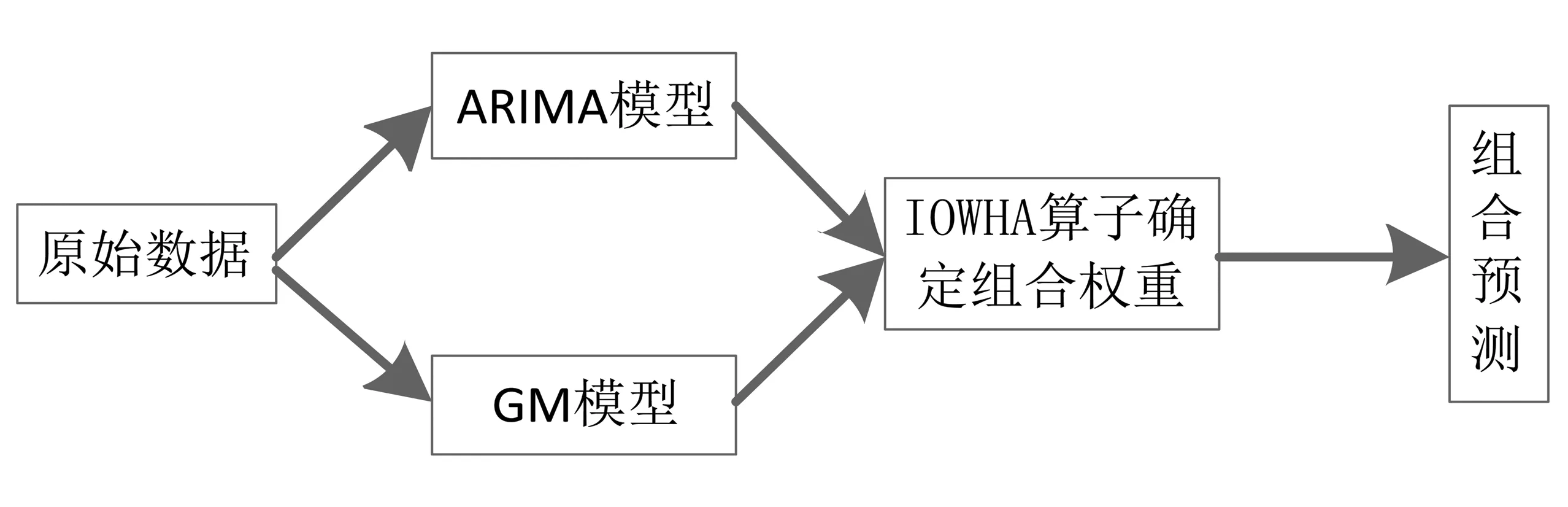
图2 组合模型预测的基本步骤

3 实例应用

3.1 数据来源与评价指标

本文数据来源于公共卫生科学数据中心，它是国家人口健康科学数据共享平台的主要数据中心之一。选取了2005-2015年河南省流行性感冒的月发病率为研究数据，共计132个样本。其中选取前120个(2005-2014年)数据作为训练样本，其余12个(2015年)数据作为检验样本，对其预测值与实际值进行比较分析，来判断组合预测模型的精度。

为了评价预测模型的预测效果和验证预测结果的精确度，通常选取均方误差(MSE)、平均绝对相对误差(MAE)、平均绝对百分比误差(MAPE)等评价指标进行模型评价。指标表达式如下：

(18)

(19)

(20)

3.2 ARIMA预测模型的建立与预测

3.2.1 数据的平稳化

采用SPSS24.0件构建ARIMA预测模型。首先判断数据序列是否具有季节性趋势。根据序列图(图3)可以看出，2005-2014年流行性感冒的月发病率呈现出比较明显的季节成分，周期长度为12个月，而且具有不平稳性，存在着一定的上升趋势。对序列进行平稳化处理，经过一阶季节差分(D=1)和一阶差分(d=1)处理后，得到的新数据序列基本稳定(图4)。

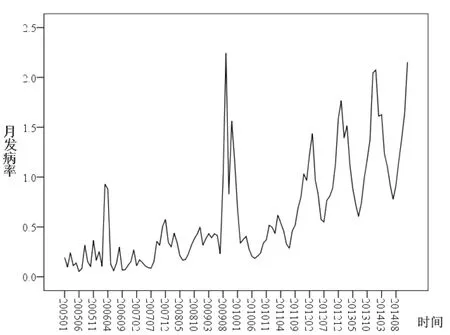
图3原始数据的序列图

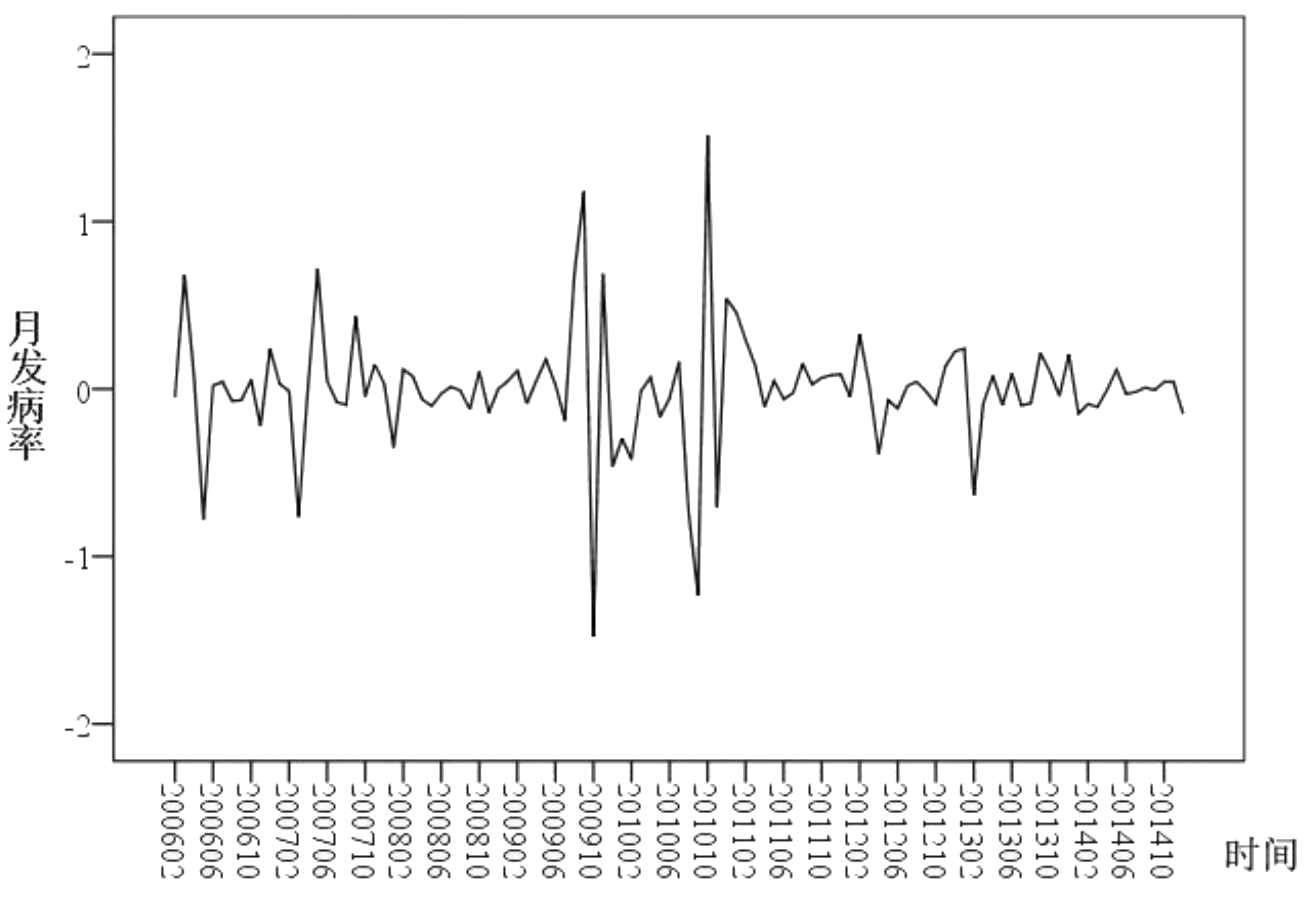
图4 一阶季节差分和一阶差分差分处理后的序列图

3.2.2 模型识别

经过一阶季节差分和一阶差分处理后，差分序列基本均匀分布在0刻度线上下两侧，差分序列是平稳的，D=1，d=1，因此可建立ARUNA(p,1,q)(P,1,Q)12(图5)。从月发病率的自相关图(ACF)和偏自相关图(PACF)可以看出，q=1，p=0、1或2，Q=0或1，P=0或1，采用BIC信息准则，即BIC值越小，模型精确度越高。各备选模型的正态化BIC值如表1所示。通过比较得出ARIMA(1,1,1)(0,1,1)12的正态化BIC值最小，即拟合效果最好。拟合效果如图6所示。由图6可以看出，实际发病率基本都在预测值95%置信区间内。

表1 模型比较

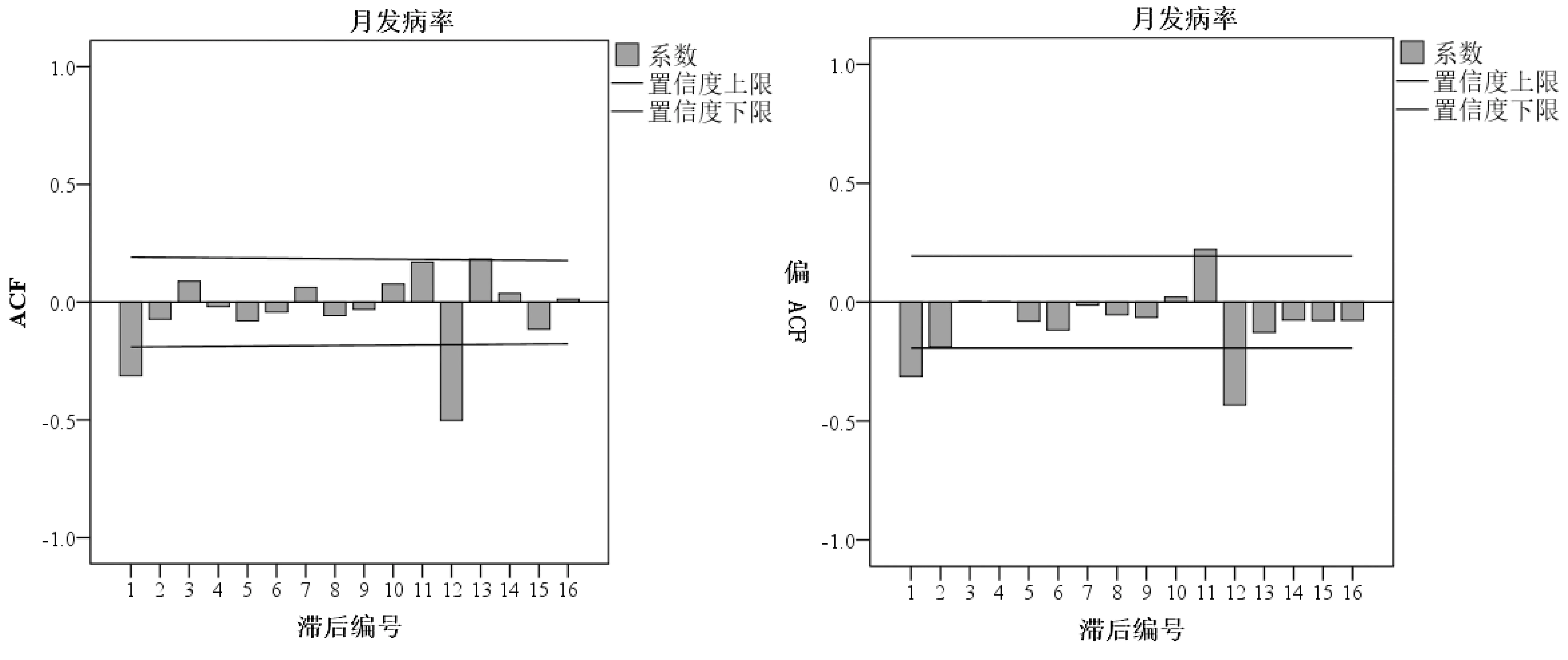
图5 月发病率的自相关图与偏自相关图

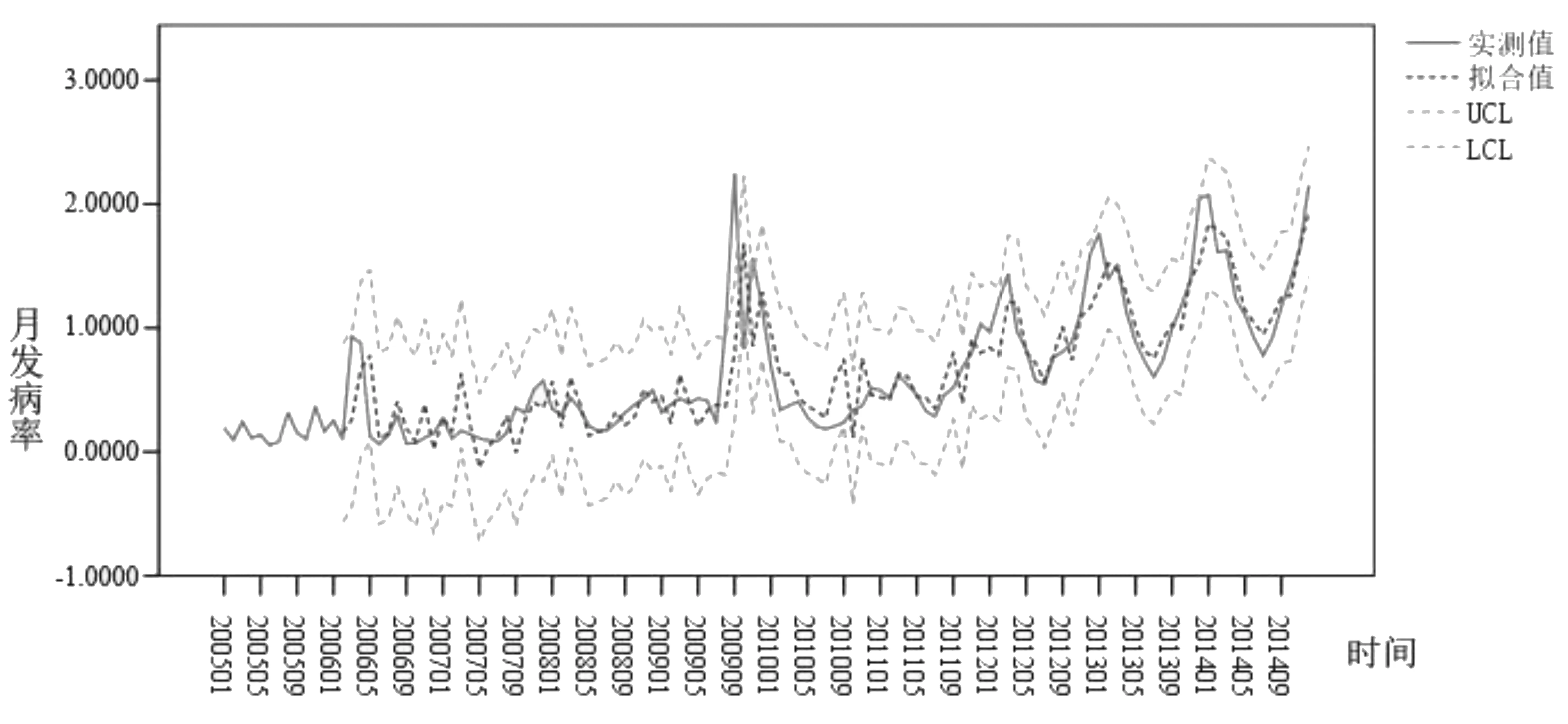
图6 ARIMA(1，1，1)(0，1，1)12模型拟合效果图

3.2.3 模型预测

利用ARIMA(1,1,1)(0,1,1)12模型预测2015年1-12月河南省流行性感冒的月发病率情况。模型预测值与实际值比较如表2所示。从表2中可以看出，实际值均落在预测值95%的置信区间内，12个月中有7个月的预测精度都在80%以上，2月、9月、10月的预测精度在70%多，只有6月、7月的预测精度在60%多。虽然预测值的波动情况和实际值相比存在差异，但总体来说，模型的预测效果较好。

表2 2015年河南省流行性感冒发病率实际值与ARIMA模型预测值(1/10万)

3.3 GM(1,1)模型预测

采用MATLAB构建GM(1,1)模型，对河南省2005-2015年流行性感冒月发病率进行预测。由原始数据的序列图可知，该序列具有较明显的周期性趋势，而灰色模型对波动大、周期型数据的预测效果并不好。我们根据周期性特征将原数据按月分为12组，即12组数据序列。根据灰色模型GM(1,1)的高预测精准性，分别对2005-2014年每月的流行性感冒发病率进行拟合，并预测出2015年每月的发病率。最后整体的拟合效果如图7所示。

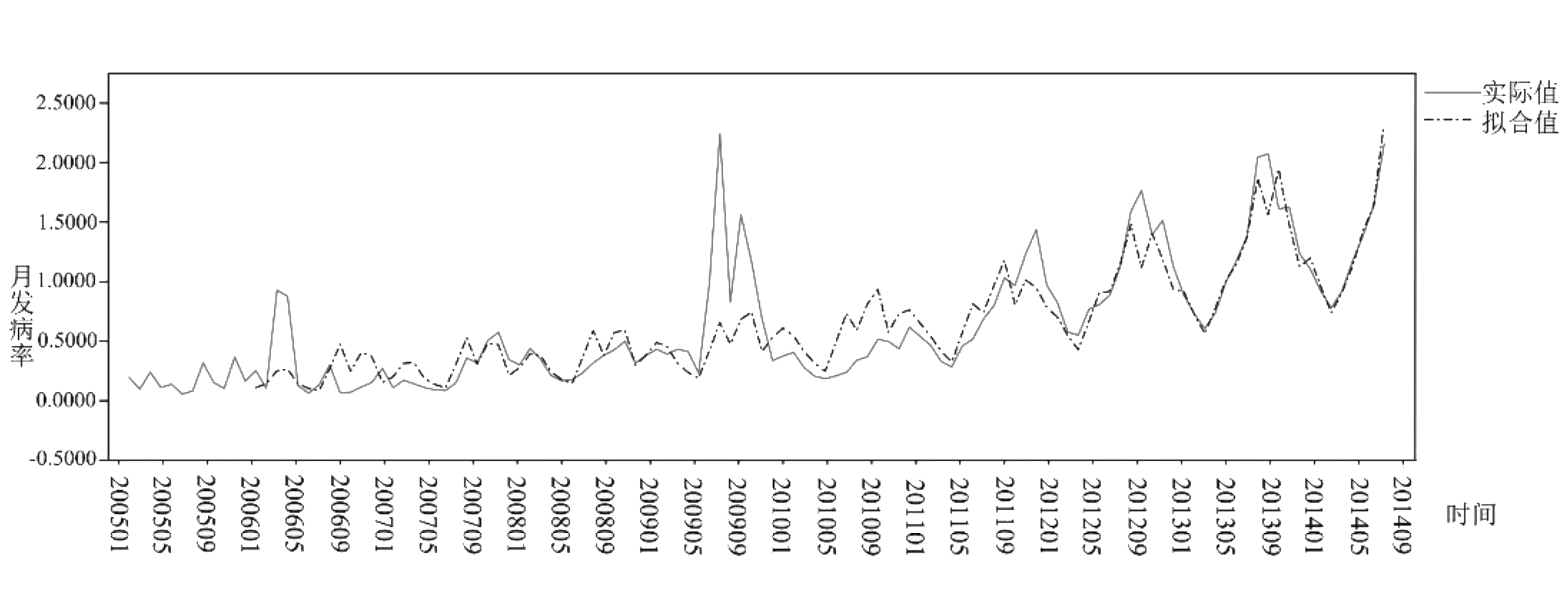
图7 GM(1,1)模型拟合效果图

从图7可以看出，除个别峰值外，拟合效果良好，说明对于季节性数据序列，灰色模型采用这种方式也能得出很好的预测效果。灰色模型对2015年每月流行性感冒发病率的预测值与实际值如表3所示。从预测精度来看，除了2月和12月的预测精度在70%以下，其他月份的预测精度都在70%以上，其中有3个月达到90%多。因此预测效果较好，但从整体来看预测性不稳定。

表3 2015年河南省流行性感冒发病率实际值与GM(1,1)模型预测值(1/10万)

3.4 改进IOWHA算子的组合模型预测值及各模型结果对比分析

根据ARIMA预测方法和为GM(1,1)预测方法，构建第t时刻预测精度与其对应模型的预测值的二维数组(a1t,X1t)，(a2t,X2t),t=1,2,…,12，代入公式(13)中计算IOWHA算子组合预测值为：

… …

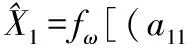
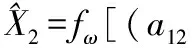
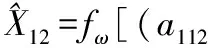
式中，ω1,ω2表示两种单项模型在组合预测模型中的加权向量。

分别算出每月基于IOWHA算子的组合预测值，将结果代入到基于Theil不等系数的IOWHA算子组合预测模型表达式中：

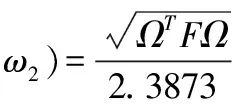
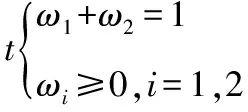
利用MATLAB求解得出组合预测模型的最优权重系数ω1=0.8564，ω2=0.1426，代入到IOWHA算子组合预测值表达式中计算得到2005年-2014年每月的流行性感冒发病率和整体的组合预测模型拟合效果(图8)及预测的2015年河南省流行性感冒月发病率(表4)。

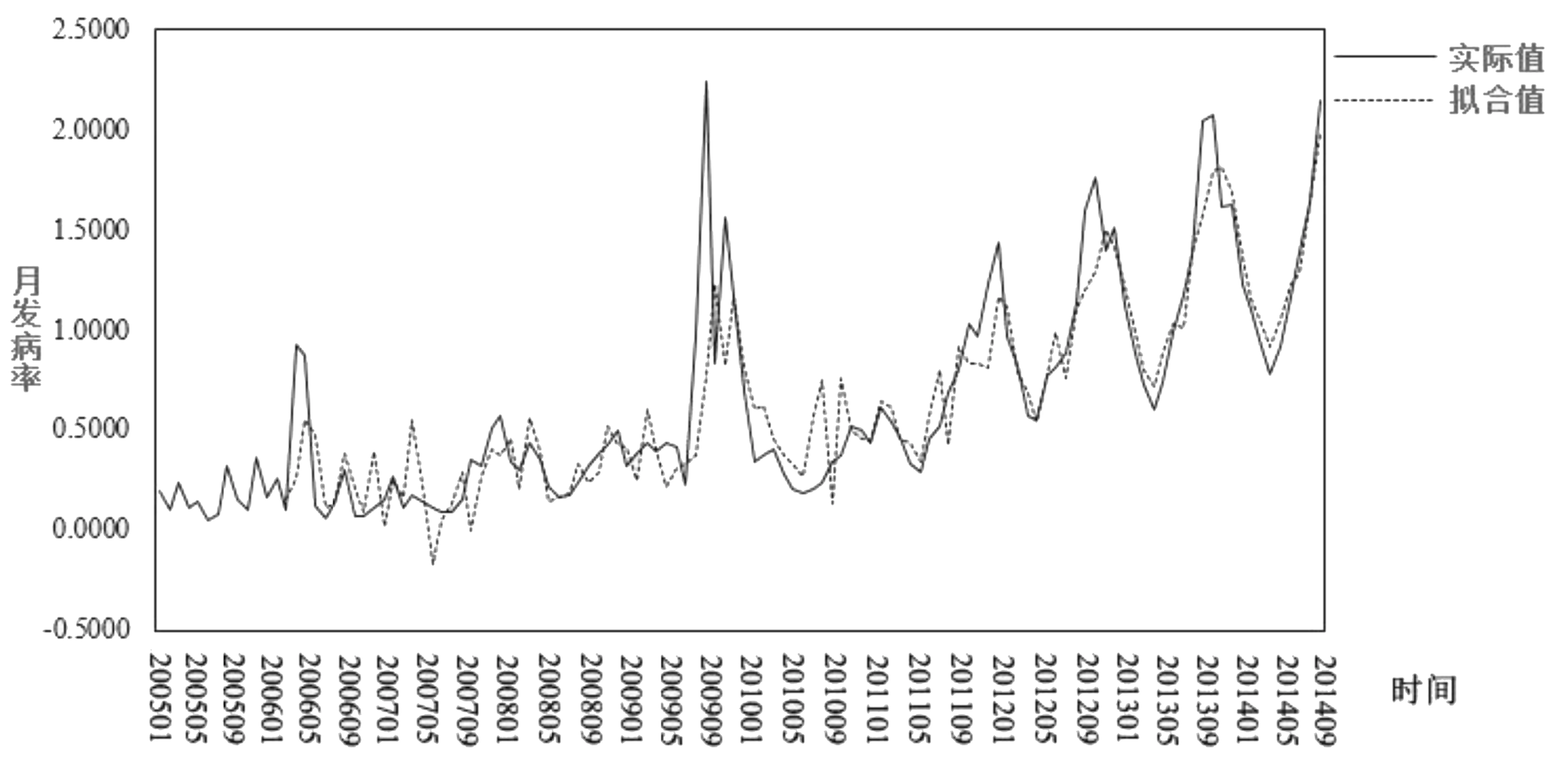
图8 组合预测模型拟合效果图

从图8中可以看出，实际值与拟合值很相近，拟合效果更好。从表4中可以看出，使用改进的IOWHA算子组合预测模型的预测值与实际值最接近，精度都在70%以上，比单项预测方法稳定且预测效果好。为了更明显地评价各种预测方法的预测效果和精确度，按照选取的预测方法评价指标，计算各种预测方法的预测效果评价结果(表5)。

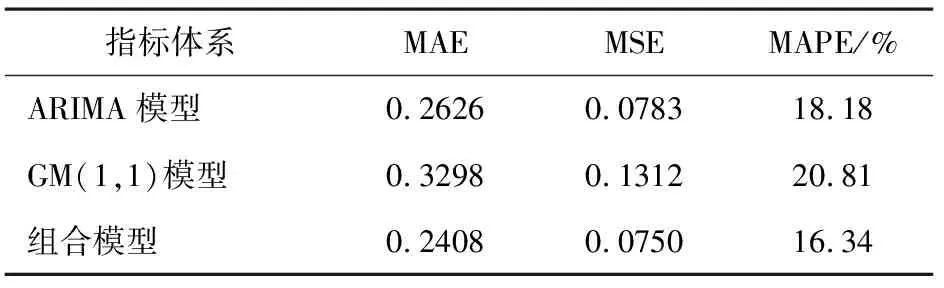
表5 各种预测方法的预测效果评价指标体系

从表5可以看出，本文创建的基于改进IOWHA算子的组合预测模型的各项指标值都低于ARIMA模型和GM(1,1)模型的指标值，说明组合模型的预测精度高于单项模型及Theil不等系数与IOWHA算子结合的组合方法的有效性和可行性。从各项指标值的大小与文献[7]中相应的各指标值相比，明显偏小，进一步证明本文的方法在一定程度上优于该文的组合预测模型，预测效果更好。另外，改进IOWHA算子的组合预测模型可以有效提高流行性感冒发病率预测的精度，并且为实现传染病发病率预测提供了可行性。

4 结语

针对传染病发病率时间序列具有非平稳性及如何提高发病率的预测精度，本文提出了一种Theil不等系数与IOWHA算子结合的组合预测模型。该模型是依据每个单项模型在各个时间点的预测精度的高低顺序赋予不同的权重，与每个时刻不同预测方法的预测精度密切相关，弥补了单项模型在预测时的缺陷。相比于目前使用的ARIMA预测模型、GM(1,1)预测模型等单项预测方法以及传统组合方法和神经网络组合方式，改进的IOWHA算子组合方式能更好地预测传染病发病率的波动趋势。通过对河南省流行性感冒发病率预测的实例，组合预测模型的预测效果评价值以及预测精度的稳定性与研究的ARIMA模型和GM(1,1)2单项模型相比，都相对更好，验证了组合预测模型的实用性。文献[7]中的ARIMA模型和GM(1,1)两个单项模型，采用的是GRNN神经网络的组合方法。从其效果评价指标MAE、MSE、MAPE的大小与本文相比可以看出，本文提出的改进IOWHA算子组合预测模型的预测精度更高，预测效果更好，可为传染病预测模型的选择提供参考。但在发病率波动较大的几个月，组合预测模型的预测精度仅有70%多，这是由传染病的随机性和非平稳性导致的。本文只考虑了历史数据中发病率的波动趋势，如果能将影响传染病的其他因素考虑在内，就可以进一步跟踪发病率的波动趋势，提高传染病发病率的预测精度。

下一步将探索预测精度更高、效果更好的单项模型，然后采用本文提出的组合预测方法进行组合验证最后的预测精度的有效性，并在本文研究基础上进一步设计和实现传染病预测系统，为传染病的预测和防控提供帮助。