基于经验模态分解的我国布鲁菌病月发病率预测研究

乔贺倩，李维德*，于国伟

布鲁菌病（Brucellosis，简称布病）是由布鲁菌属的细菌侵入机体，引起传染-变态反应性的人畜共患传染病。自1905年我国首次报告布病发病患者以来，感染布病的人数逐年增加，尤其是90年代后期，布病疫情越发严重，引起我国有关部门的关注，而预防和控制布病成为当前的重要课题［1］。当前学者对布病的研究主要侧重于对已发生的疾病案例进行流行病学特征分析［2］和时空分布研究［3］，对布病发病率预测的研究较少，而发病率的预测可以改善传染病的预防工作，更好地控制疫情［4］。布病发病率为每10万人中感染布病的人数，发病率预测属于时间序列分析，主要方法有乘积季节模型（SARIMA）［5］、GM（1，1）灰色模型［6］、状态空间模型［7］、趋势外推法［7］、支持向量机（SVM）模型［8］、神经网络［9］等。这些单一模型预测误差大，不能对发病率做出准确预测，为了提高预测精度，可以将组合模型用于发病率预测［10］。此外，基于原始时间序列的建模很难处理序列的非线性、非平稳特征，近年来提出的经验模态分解（EMD）可以突出序列局部特征，具有自适应的优点［11］。本研究将EMD和时间序列分析方法结合起来，首先用EMD把发病率序列分成高低频本征模态函数（IMF）分量和趋势项，然后用SVM预测IMF分量，用自回归移动平均模型（ARIMA）预测趋势项，最后，将各个模型的预测值进行加权求和，得出布病月发病率预测值，结果表明，本研究提出的方法能够有效提高预测精度，降低预测误差。现报道如下。

1 资料与方法

1.1 数据来源 本研究数据来源于2004年1月—2016年12月全国布病月发病率序列（共156组），其中2004年1—12月布病发病率数据来源于公共卫生科学数据中心的统计资料，2015年1月—2016年12月发病人数数据来源于国家卫生计生委疾病预防控制局全国法定传染病疫情概况，并且根据2014、2015年年末常住人口总数分别计算2015、2016年布病月发病率。

实证过程中，选取2004年1月—2015年12月（共144组）的数据作为训练集以建立预测模型，2016年1—12月（共12组）的数据作为测试集以验证模型和算法的有效性。

1.2 相关理论知识

1.2.1 EMD EMD是1998年美国华裔工程师HUANG等提出的［12］，其是一种新型自适应信号时频分析方法，特别适用于非线性、非平稳信号的分析处理。EMD算法可以将时间序列分解成若干个IMF，即将原信号分解为许多窄带分量，每一分量被称为IMF，也就是说，一个多重信号（s）由若干IMF和1个残余信号（r）组成：，其中，s(t)表示原始信号，imfi(t)表示第i个本征模态函数，i=1,…, n，rn(t)表示残余信号。

IMF需要满足以下2个条件：（1）信号中的零点数目和极值点数目相等或至多相差1个；（2）极大值包络线和极小值包络线的均值相等且为零。

EMD过程中，随着分解程度的加深，IMF分量的波动频率不断降低，从而产生了高频IMF分量和低频IMF分量。EMD得到的重构信号与原始信号之间只相差一个趋势项，因而用EMD算法分解时间序列可以准确地提取序列不同时间段的波动特征，为进一步的预测提供准确的数据支持［12］。

1.2.2 SVM模型 SVM模型是由VAPNIK提出的［13］，主要用于模式分类和线性回归，其通过不同核函数，把低维数据映射到高维特征空间中，使低维线性不可分转换成高维线性可分。用SVM模型进行回归预测时，惩罚参数c和核函数参数g会影响预测准确率，因此选择合适的参数才可以达到理想的预测效果；比较常见的参数寻优方法有遗传算法（GA）和粒子群优化算法（PSO）等。参数寻优结束后，就可以构建SVM模型，具体建模过程见图1［13］。

1.2.3 ARIMA

1.2.3.1 疏系数模型 ARIMA中，如果有部分自相关系数或部分移动平均系数缺省，那么该模型就称为疏系数模型。如果自相关系数缺省，疏系数模型简记为ARIMA((p1,…,pm),d,q)；移动平均系数缺省，模型简记为ARIMA(p,d,(q1,…,qn))；二者均缺省，模型简记为ARIMA((p1,…,pm),d,(q1,…,qn))。疏系数模型可以更好地拟合序列不规则波动，改善ARIMA的预测精度［13］。

1.2.3.2 SARIMA SARIMA可以用于处理复杂季节效应，即序列的季节效应、长期趋势和随机波动之间有复杂的交互影响关系。当序列具有短期相关性时，通常用低阶ARMA(p,q)提取；当序列具有季节效应时，季节相关性用以周期步长为单位的ARMA(P,Q)提取。SARIMA一般简记为ARIMA(p,d,q)×(P,Q,D)s［14］。

1.2.4 模型评价标准 根据绝对百分比误差（APE）、均方根误差（RMSE）、平均绝对误差（MAE）、平均绝对百分比误差（MAPE）评价模型的预测精度，计算公式为：。其中yi为实际值，为^y预测值，n为样本数。

1.3 本研究我国布病月发病率预测方法 本研究基于EMD和时间序列分析进行我国布病月发病率预测，其步骤如下：（1）用EMD算法分解2004年1月—2016年12月全国布病月发病率序列，得到n个高、低频IMF分量和1个余量（趋势项）。（2）选取2004年1月—2015年12月的IMF分量和趋势项，对每个IMF分量建立SVM模型，对趋势项建立ARIMA（疏系数模型）；根据所建立的模型得到2004—2015年n个IMF分量和趋势项的拟合值；然后选择合适的权重，对拟合值进行线性加权，得出2004—2015年的布病月发病率。（3）根据所建立的模型，计算2016年1—12月的n个IMF分量和趋势项的预测值，用上一步中确定的权重将这些预测值线性加权，得出2016年1—12月的布病发病率预测值，最后比较预测值和实际值之间的差异，计算模型预测误差。（4）采用上述模型预测2017年1—12月的n个IMF分量和趋势项，加权得出2017年各月布病发病率预测值。

1.4 统计学方法 采用Matlab 2012a和Eviews 7.0软件进行数据分析，SVM模型建立使用SVM_GUI工具箱。采用t检验判断ARIMA模型参数是否显著。以P＜0.05为差异有统计学意义。

2 结果

2.1 EMD 对2004年1月—2016年12月全国布病月发病率原始序列（见图2）进行EMD，得到4个IMF分量和1个趋势项，不同IMF分量的波动程度有很大差异，IMF1、IMF2和IMF3代表高频分量，波动幅度比较大，IMF4代表低频分量，波动幅度较小；趋势项表明布病月发病率呈逐年上升趋势（见图3）。

2.2 建立模型

2.2.1 SVM模型 对IMF1～IMF4分别构建SVM模型。以2004年1月—2015年12月的布病发病率作为训练数据（以2004年1月—2015年11月的布病发病率作为输入自变量，2004年2月—2015年12月的布病发病率作为输出因变量），2016年1—12月的布病发病率作为测试数据（以2015年12月—2016年11月的布病发病率作为输入自变量，2016年1—12月的布病发病率作为输出因变量），对IMF1～IMF4进行预处理，并用智能算法寻找建立SVM模型的最优参数c、g，方法和结果见表1。

选取最优参数后，用这些参数训练4个SVM模型，最后得出2004年1月—2015年12月IMF1～IMF4的拟合值和2016年1—12月IMF1～IMF4的预测值，根据2016年1—12月IMF1～IMF4的预测值和实际值，做出对比曲线。结果显示，2016年1—5月IMF1～IMF4的预测值和实际值有较小差异，2016年6—12月，IMF1～IMF4的预测值和实际值很接近，说明SVM模型可以准确预测IMF1～IMF4的实际值，而且模型较为稳定（见图4～7）。

2.2.2 ARIMA 对趋势项建立ARIMA疏系数模型，先对趋势项进行单位根（ADF）检验，发现趋势项是非平稳序列，再对其进行一阶差分使趋势项成为平稳序列，之后根据一阶差分后的序列判断ARIMA的阶数，通过赤池信息量准则（AIC），得出最优模型为ARIMA((1,12,24),1,0)，模型参数均有统计学差异（P＜0.05，见表2）。

图1 SVM模型构建过程Figure 1 Building process of SVM model

图2 布病发病率原始序列Figure 2 Original sequence of monthly incidence of brucellosis in China during January 2004 to December 2016

图3 EMD后的各分量和趋势项Figure 3 Each IMF component and trend term after EMD

表1 数据预处理方法和参数寻优算法Table 1 Algorithm of data preprocessing and parameter optimization

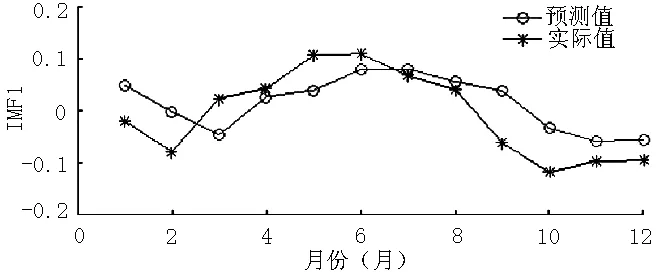
图4 2016年1—12月IMF1的预测值和实际值Figure 4 Predicted value and actual value of IMF1 in 2016

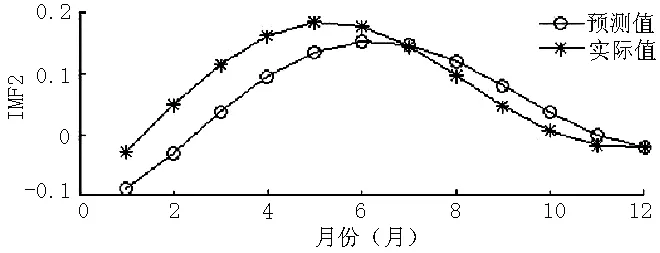
图5 2016年1—12月IMF2的预测值和实际值Figure 5 Predicted value and actual value of IMF2 in 2016

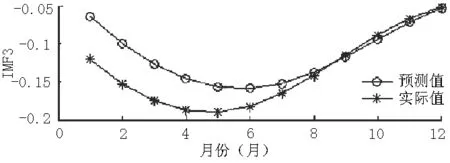
图6 2016年1—12月IMF3的预测值和实际值Figure 6 Predicted value and actual value of IMF3 in 2016

图7 2016年1—12月IMF4的预测值和实际值Figure 7 Predicted value and actual value of IMF4 in 2016

根据最优模型ARIMA((1,12,24),1,0)，预测2016年1—12月的趋势项，与实际值进行对比，结果显示，2016年1—12月趋势项的预测值和实际值之间几乎重合，表明所建立的ARIMA疏系数模型预测准确度较高（见图8）。

2.3 模型预测 在IMF1～IMF4和趋势项的模型建立完成之后，将这5个模型输出值相加，即可得出最终布病发病率预测值。IMF1～IMF4的权重根据SVM训练数据集的均方误差（MSE）计算得出，结果见表3。计算过程中，给MSE较小的IMF1和IMF4较大的权重，MSE较大的IMF2和IMF3较小的权重，这样可以避免预测误差较大的分量影响发病率的预测。趋势项的权重设为0.8时预测效果较好，即W5=0.8。

分量和趋势项权重确定之后，把训练数据集2006年2月—2015年12月的各分量和趋势项线性加权相加，得出相应的全国布病月发病率拟合值，发现如果将拟合值滞后一期，可以提高拟合效果。所以对于测试数据集，把2016年1—12月的各分量和趋势项的预测值加权求和之后，同样滞后一期，最终得出测试样本布病月发病率预测值，并与布病月发病率实际值进行对比，结果显示，2016年1—11月的布病月发病率的预测值和实际值相差较小（见图9）。再计算2016年1—11月的布病月发病率预测值的APE，结果显示，2016年1—11月布病月发病率预测值的MAPE为0.066 5，各月的APE大多＜0.070 0，数值偏小（见表4），表明本研究方法可以准确预测我国布病月发病率。

表2 ARIMA参数估计结果Table 2 Parameter estimation of ARIMA

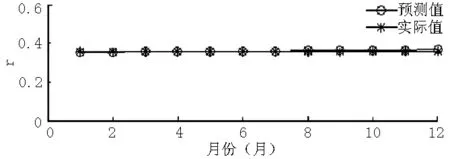
图8 2016年1—12月趋势项的预测值和实际值Figure 8 Predicted value and actual value of r in 2016

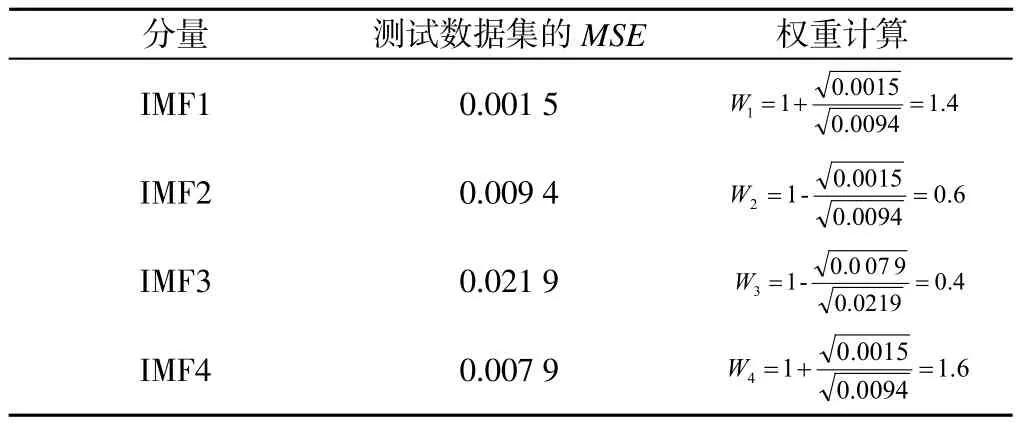
表3 IMF1～IMF4的RMSE及权重计算Table 3 MSE of IMF1～IMF4 and weight calculation

为了对比本研究提出方法的预测效果，选择单一SVM模型和SARIMA对未分解的序列建模［15］，并预测2016年1—11月布病发病率，根据RMSE、MAE、MAPE这3个指标评价模型的预测精度，结果显示，本文提出的基于EMD的分析方法，明显优于未分解的单一模型，预测误差均减小，预测精度较高（见表5）。

最后根据本研究提出的预测方法，对2017年1—12月的布病月发病率进行预测，预测结果见表6。

3 讨论

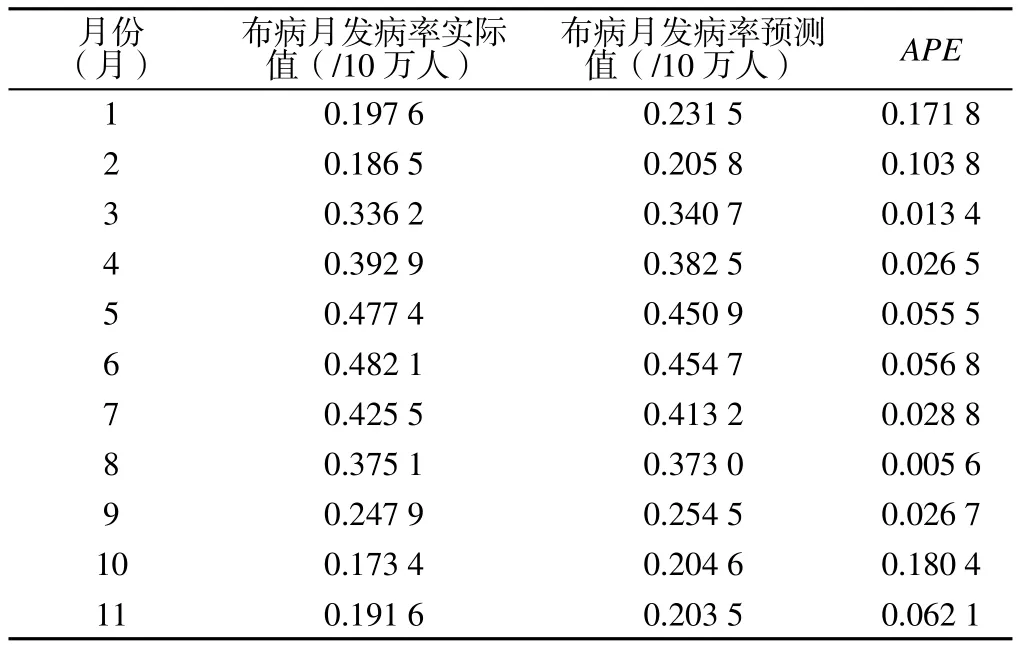
表4 2016年1—11月布病月发病率预测值的APETable 4 APE of predicted value of monthly incidence in China from January to November 2016

表5 三种模型预测精度比较Table 5 Prediction accuracy of three models

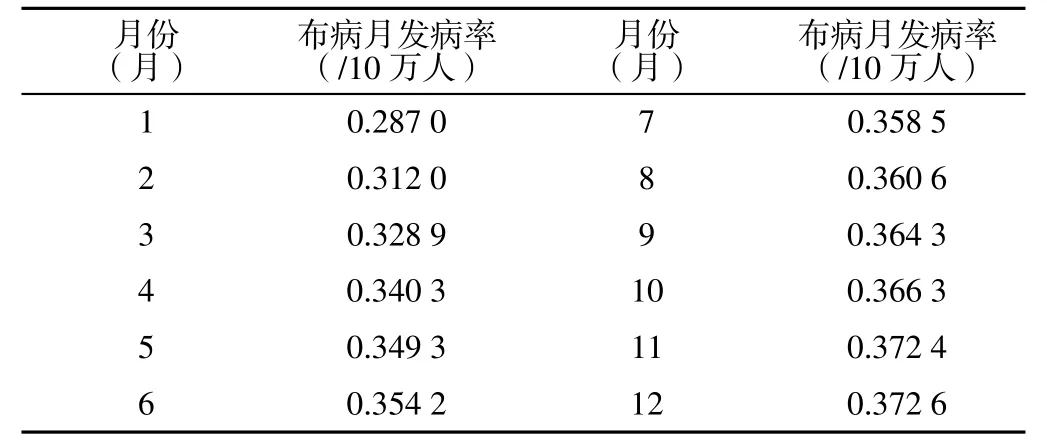
表6 2017年1—12月布病月发病率预测结果Table 6 Predicted value of monthly incidence of brucellosis in China in 2017

3.1 我国布病发病率的时间特征 本研究结果显示，2004—2016年布病月发病率逐年上升，全国范围内感染布病的病例数不断增加，表明布病传染没有得到很好的控制［16］，以后要着重完善布病的预防控制工作。此外，布病月发病率有很明显的季节性特点。一般而言，各年份1～4月布病发病率不断上升，5、6月到达发病高峰期，7～12月发病率逐渐降低，这表明季节因素对布病月发病率有很大影响，因而预测模型必须充分考虑季节因素的影响，提取不同时间段布病发病率波动的特征。本研究提出的预测方法精度较高，可以准确反映布病月发病率的时间波动。

3.2 本研究方法的创新性和不足之处 本研究根据我国布病月发病率数据的波动特性，采用EMD算法将其分解为IMF1～IMF4和趋势项，对IMF1～IMF4建立SVM模型，对趋势项建立ARIMA疏系数模型，之后将上述5个模型输出值进行线性加权求和，得出布病月发病率预测值，结果表明，和针对未分解序列的单一SVM模型、SARIMA相比，本研究所提出的方法能有效地提高预测精度，降低预测误差。并且，本研究还给出了2017年1—12月的布病发病率预测值。近年来，大多数对发病率进行预测的文献，均是对原始发病率序列进行建模，如黄德生等［17］、朱杰等［18］用SVM模型预测肾出血热和肝炎发病率。本文通过EMD将原始发病率序列分成4个高、低频IMF分量和1个趋势项，没有直接使用原始序列，分解之后的序列反映了发病率不同时间段的波动特征，针对每个序列的不同，选择合适的模型进行预测，最后将预测值线性加权后得出发病率。这种分析方法可以准确预测发病率的季节波动，提高预测精度。然而，布病作为一种传染病，其传播会受到其他各种外界因素如温度、湿度、自然和人文环境等的影响，本研究预测时只考虑了时间因素对发病率的影响，没有考虑外生变量。在以后的研究中，可以将其他影响因素加入到模型中，以更加准确地预测布病月发病率［19］。

综上所述，本研究根据相关发病率数据构建了基于EMD和时间序列分析的我国布病月发病率预测模型，其预测误差较小，预测准确度较高；2017年1—12月布病发病率预测值为0.287 0/10万人～0.372 6/10万人。以本研究结果可以为我国布病预防控制工作提供一定的数据支持。

作者贡献：乔贺倩、李维德、于国伟进行文章的构思与设计；乔贺倩、于国伟负责研究的实施与可行性分析、数据收集、数据整理和结果的分析与解释；乔贺倩撰写论文；李维德、于国伟进行论文的修订，负责文章的质量控制及审校，并对文章整体负责，监督管理。

本文无利益冲突。

［1］王大力，李晔.布鲁杆菌病防控策略的回顾与思考［J］.中华地方病学杂志，2015，34（5）：313-314.DOI：10.3760/cma.j.issn.2095-4255.2015.05.001.

WANG D L，LI Y.Review and consideration of brucellosis prevention and control strategy［J］.Chinese Journal of Endemiology，2015，34（5）：313-314.DOI：10.3760/cma.j.issn.2095-4255.2015.05.001.

［2］李淑梅，李东春.绥中县2004—2012年布鲁氏菌病流行病学分析［J］.中国公共卫生，2014，30（2）：237-239.DOI：10.11847/zgggws2014-30-02-36.

LI S M，LI D C.Prevalence of brucellosis in Suizhong county from 2004 to 2012［J］.Chinese Journal of Public Health，2014，30（2）：237-239.DOI：10.11847/zgggws2014-30-02-36.

［3］曹宁，闫涛，朱浩，等.2010—2014年锡林郭勒盟重点人群布病发病率趋势分析［J］.世界最新医学信息文摘（电子版），2016，16（76）：50-51.DOI：10.3969/j.issn.1671-3141.2016.76.025.

CAO N，YAN T，ZHU H，et al.Variation tendency analysis of prevalence of incidence rate of human brucellosis for key populations in Xilin Gol League During 2010—2014［J］.World Latest Medicine Information （Electronic Version），2016，16（76）：50-51.DOI：10.3969/j.issn.1671-3141.2016.76.025.

［4］石凌云.2011—2015年武陟县布鲁氏杆菌病流行动态及疫情分析［J］.医学理论与实践，2016，29（14）：1960-1961.DOI：10.19381/j.issn.1001-7585.2016.14.083.

SHI L Y.Epidemic dynamics and situation analysis of brucellosis in Wuzhi County during 2011—2015［J］.The Journal of Medical Theory and Practice，2016，29（14）：1960-1961.DOI：10.19381/j.issn.1001-7585.2016.14.083.

［5］田德红，丁国武，于国伟，等.自回归求和移动平均乘积季节模型在我国布鲁菌病短期月发病人数预测中的应用［J］.中 国 全 科 医 学，2015，18（33）：4100-4104.DOI：10.3969/j.issn.1007-9572.2015.33.017.

TIAN D H，DING G W，YU G W，et al.Application of multiple seasonal ARIMA model in forecasting monthly prevalence of brucellosis in China［J］.Chinese General Practice，2015，18 （33）：4100-4104.DOI： 10.3969/j.issn.1007- 9572.2015.33.017.

［6］杨永利，毛赛彩，薛源，等.GM（1，1）和趋势外推模型在我国艾滋病发病率预测中的应用［J］.中国卫生统计，2014，31（6）：952-954.

YANG Y L，MAO S C，XUE Y，et al.Prediction on the incidence rate of AIDS in China with gray model（1，1） and trend extrapolation model［J］.Chinese Journal of Health Statistics，2014，31（6）：952-954.

［7］陈友春，朱文婕.状态空间模型及其在传染病发病率预测中的应用［J］.南京医科大学学报（自然科学版），2015，35（2）：275-278.DOI：10.7655/NYDXBNS20150233.

CHEN Y C，ZHU W J.State space model and its application on forecasting in incidence of infectious disease［J］.Journal of Nanjing Medical University（Natural Science），2015，35（2）：275-278.DOI：10.7655/NYDXBNS20150233.

［8］谢骁旭，袁兆康.基于R的江西省肺结核发病率ARIMA-SVM组合预测模型［J］.中国卫生统计，2015，32（1）：160-162.

XIE X X，YUAN Z K.Using R to fit a hybrid ARIMA and support vector machines model in tuberculosis incidence forecasting of Jiangxi Province［J］.Chinese Journal of Health Statistics，2015，32（1）：160-162.

［9］叶晓军，沈毅，任茹香，等.基于GRNN的组合预测模型在传染病发病率预测中的应用［J］.浙江预防医学，2012，24（1）：8-13.DOI：10.3969/j.issn.1007-0931.2012.01.003.

YE X J，SHEN Y，REN R X，et al.Application of a combination forecasting model based on GRNN for incidence of pulmonary tuberculosis［J］.Zhejiang Journal of Preventive Medicine，2012，24（1）：8-13.DOI：10.3969/j.issn.1007-0931.2012.01.003.

［10］谢骁旭.基于R的江西省肺结核发病率ARIMA-SVM组合预测模型［D］.南昌：南昌大学，2015.

［11］王韶，杨江平，李逢兵，等.基于经验模式分解和神经网络的短期风速组合预测［J］.电力系统保护与控制，2012，40（10）：6-11，18.DOI：10.3969/j.issn.1674-3415.2012.10.002.

WANG S，YANG J P，LI F B，et al.Short-term wind speed forecasting based on EMD and ANN［J］.Power System Protection and Control，2012，40（10）：6-11，18.DOI：10.3969/j.issn.1674-3415.2012.10.002.

［12］岳相臣.经验模态分解算法应用研究［D］.西安：西安电子科技大学，2013.

［13］王小川，史峰，郁磊，等.MATLAB神经网络43个案例分析［M］.北京：北京航空航天大学出版社，2013：102-179.

［14］王燕.应用时间序列分析［M］.3版.北京：中国人民大学出版社，2013：141-152.

［15］田中大，李树江，王艳红，等.经验模式分解与时间序列分析在网络流量预测中的应用［J］.控制与决策，2015，30（5）：905-910.DOI：10.13195/j.kzyjc.2014.0453.

TIAN Z D，LI S J，WANG Y H，et al.Network traffic prediction based on empirical mode decomposition and time series analysis［J］.Control and Decision，2015，30（5）：905-910.DOI： 10.13195/j.kzyjc.2014.0453.

［16］蒲秀华，陈睿.1967—2013年甘肃省高台县人间布鲁氏菌病防治效果分析［J］.疾病预防控制通报，2014，29（2）：46-47.DOI：10.13215/j.cnki.jbyfkztb.1312022.

PU X H，CHEN R.Control effect of human brucellosis in Gaotai County of Gansu province in 1967—2013［J］.Bulletin of Disease Control and Prevention （China），2014，29（2）：46-47.DOI：10.13215/j.cnki.jbyfkztb.1312022.

［17］黄德生，沈铁峰，吴伟，等.基于支持向量机的肾综合征出血热疫情预测［J］.中国媒介生物学及控制杂志，2008，19（6）：557-559.DOI：10.3969/j.issn.1003-4692.2008.06.020.

HUANG D S，SHEN T F，WU W，et al.The prediction of hemorrhagic fever with renal syndrome based on support vector machine［J］.Chinese Journal of Vector Biology and Control，2008，19（6）：557-559.DOI：10.3969/j.issn.1003-4692.2008.06.020.

［18］朱杰，朱昆鹏，沈迎.使用最小二乘支持向量机技术预测传染病发病率的研究［J］.职业与健康，2012，28（21）：2662-2664.DOI：10.13329/j.cnki.zyyjk.2012.21.010.

ZHU J，ZHU K P，SHEN Y.Study on a forecasting model for infectious disease incidence rate based on least squares support vector machine［J］.Occupation and Health，2012，28（21）：2662-2664.DOI：10.13329/j.cnki.zyyjk.2012.21.010.

［19］WEI W，JIANG J，LIANG H，et al.Application of a combined model with Autoregressive Integrated Moving Average（ARIMA）and Generalized Regression Neural Network（GRNN） in forecasting hepatitis incidence in Heng County，China［J］.PLoS One，2016，11（6）：e0156768.DOI：10.1371/journal.pone.0156768.