施工期应变计组监测资料分析

刘千驹

（中国电建集团西北勘测设计研究院有限公司，陕西西安，710065）

0 引言

大量的工程实践表明［1］，混凝土应力应变监测资料分析可以有效评估相应结构物运行的安全状况，其反馈的信息还可以对设计、施工及运行管理等起到一定的指导作用。混凝土应力应变采用应变计（组）监测，在混凝土中按需要通常埋设九向、五向、三向、二向应变计组及单向应变计。应变计（组）监测的是传感器埋设方向的应变，该应变包含温度应变、混凝土自生体积应变、徐变应变等。工程上往往更关注的是结构物混凝土承受应力状况。而混凝土应力计算主要是利用应变计（组）监测到的混凝土应变，扣除旁边配套埋设的无应力计的应变测值后，依据广义胡克定律换算成单轴应变，然后根据混凝土的弹模和徐变试验资料，用变形法计算出各方向正应力，再用正应力计算剪应力，并求得主应力及其方向余弦。

结合国内某水电工程施工期厂房坝段安装的五向应变计组测值，运用变形法，并基于MATLAB计算及绘图程序，综合分析该工程施工期厂房坝段监测断面应力分布及变化状况。

1 混凝土应力计算

现以五向应变计组为例进行应力分析，其他应变计组可依此类推。五向应变计组安装埋设示意图见图1。

图1 五向应变计组安装埋设示意图Fig.1 Installation of the five-direction strain gauge

1.1 应变计组测值平衡修正

混凝土是粘塑弹性体，应变计测值为综合应变，包括应力引起的应变及非应力引起的应变，通常可用下式表示：

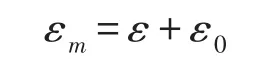
式中：εm——应变计测值；ε——混凝土应力应变；ε0——无应力计测值。

在大体积混凝土内部埋设的应变计组，一般认为是代表点应力状态的一个测点，而混凝土被认为是均质的各向同性体，根据弹性理论，点应力的任何三正交轴向的应变量之和均应相等。即：

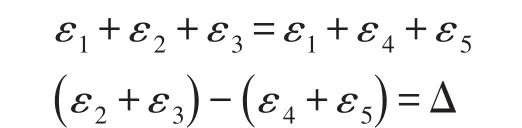
式中：Δ——不平衡量，是观测误差（包括过失误差、偶然误差以及系统误差）。设修正后的应变量分别为 δ2、δ3、δ4、δ5。其中：δi=εi-Δ 4。

依据五向应变计组的空间布置，推出正应变与剪应变的计算公式。

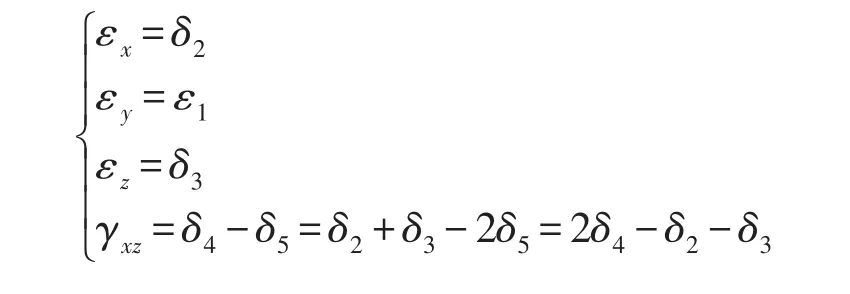
1.2 空间应变换算单轴应变

由于混凝土徐变试验是在单轴条件下进行的，应力状态为简单的单向应力状态，而大坝内部的应变计各测点往往处在复杂的空间应力状态，因此根据广义胡克定律将空间状态下各测点应变换算成单轴应变。单轴应变公式如下：

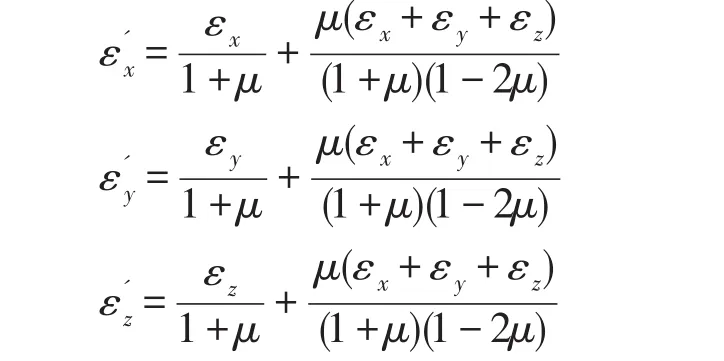
式中：εx、εy、εz——应变计扣除无应力计x、y、z方向的测值，——对应的单轴应变；μ——泊松比。

1.3 变形法计算正应力

在单向受力情况下，混凝土试件在时间t内的单轴应力应变可以表示为：

ε'(t)=εc(t)+εe(t)

式中：εc(t)——徐变弹变；εe(t)——弹性应变。

将单轴应变换算成单轴应力时，还需采用应变计埋设处的混凝土弹模和徐变试验资料［2］。根据徐变试验资料，将时间划分n个时段，每个时段的起始和中止时刻（龄期-）分别为：τ0,τ1,τ2,…,τn-1,τn，各时间段的中点龄期：τi=(τi+τi-1) 2。各时刻对应的单轴应变为。则混凝土徐变应变在一维应力状态下的表达式为：

将式中 Δσi和 ε'(n)移项后，可得出在龄期的应力增量为：

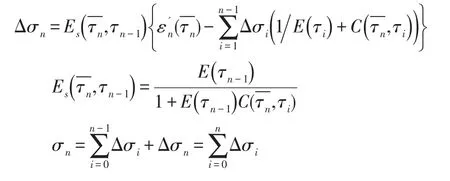
1.4 主应力计算

对于五向应变计组，只有ZX面有45°和135°应变计，因此，只能计算XZ平面内的主应力：

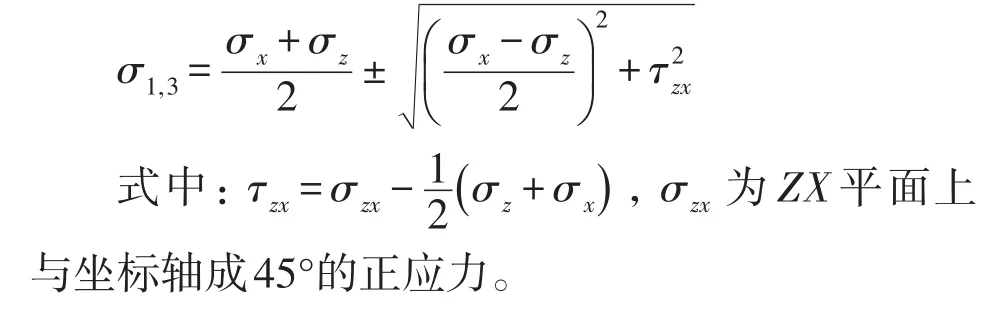
2 MATLAB应力算法实现

根据上述五向应变计组测值的应力计算过程，采用MATLAB编写应力计算程序并绘图。程序流程如下：

（1）监测数据可靠性检查甄别，通过绘制监测数据过程线，人工对跳变的数据进行粗差剔除或修正。

（2）根据应变计组各方向的应变计测值，按1.1节，对测值进行弹性力学平衡验证，对不满足条件的五向应变计组测值进行平衡修正。

（3）根据1.2节公式将五向应变计组空间应变转换成混凝土徐变试验条件下的单轴应变。

（4）依据变形法的递推公式，计算应变计组各方向的徐变应力值。

（5）依据1.4节理论计算五向应变计组各方向的主应力。

3 工程实例

现以国内在建的某碾压混凝土坝工程为例进行计算。该工程以发电为主，拦河坝最大坝高75.0m，坝顶高程1 820.50 m，电站装机容量420 MW（3×140 MW）。坝体内部混凝土应力应变监测主要采用五向应变计组，五向应变计基本布置在厂房坝段。目前施工期部分五向应变计测值较大，接近仪器的量程。结合混凝土相关试验资料对已安装的4套五向应变计组进行混凝土应力计算。五向应变计组具体安装埋设位置见图2和表1。

表1 五向应变计埋设位置统计表Table 1 Statistics of the embedment location of the five-direction strain gauges

3.1 五向应变计监测资料分析

根据五向应变计组实测值绘制的混凝土应变及温度变化过程线见图3。

从过程线可以看出：混凝土应变测值受温度影响较大，两者具有高度的相关性。经应变平衡计算，S512-CF应变不平衡量基本在120 με左右，其余各应变计组的应变不平衡量基本在60 με以内，应变计组应变不平衡量偏大。应变计组应力应变测值主要受温度变化影响，而温度在混凝土浇筑初期受水化热变化影响较大，导致初期应力应变变化较大，随后变化逐步趋于平稳。目前除应变计组S512-CF外，其余应变计组的应力应变测值在-200～150 με之间，测值变化总体稳定；S512-CF应变测值变化偏大，其测值在-200～1 000 με之间。目前最大变形发生在S512-CF应变计组2号（XZ平面45°）和4号测点所在部位。在厂房坝段肘管下部，沿坝轴线方向为拉应变。埋设在相同部位钢筋计拉应力值较大，测值在113.1～131.7 MPa之间。

图2 五向应变计安装埋设位置示意图Fig.2 Embedment locations of the five-direction strain gauges

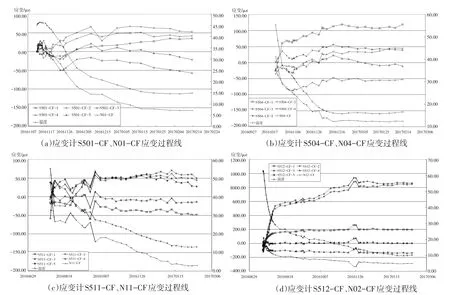
图3 五向应变计组应变及温度测值变化过程线Fig.3 Graph of temperature and the strain monitored by the five-direction strain gauges

埋设的4支无应力计主要监测混凝土自生体积变化情况。自生体积变化过程是混凝土在水化过程中由于化学作用而产生的形变，随着水化过程结束而逐渐趋向稳定，基本上保持单调收缩变化。如图3中有个别测点出现了不单调变化，初步分析可能是受外界温度影响，造成无应力计测值中包含温度应变，不完全是无应力状态。

综上分析，各应变计组的应变不平衡性较大，且无应力计测值包含温度应变，两者对混凝土应变计算的成果精度存在一定影响。

3.2 应力计算结果分析

根据混凝土应变计算并绘制混凝土应力测值过程线见图4，应力特征值统计见表2。

由上述图表可以看出，S512-CF应变计所在部位混凝土应力较大，最大拉应力达3.00 MPa，最大压应力0.89 MPa，测值变化目前趋于稳定状态。依据混凝土配合比试验报告，厂房坝段混凝土28 d抗拉强度3.51 MPa，拉应力还在允许范围内。其余各测点由于仪器监测时间较短，测值变化明显，但量值不大，均在混凝土应力允许范围内，拉应力均在0.3 MPa以下，压应力在0.1 MPa以内。

垂直方向（Z向）应力分析成果：在应变计组埋设初期，测点部位混凝土呈现受拉状态，随着混凝土浇筑高程的升高，Z向混凝土压应力保持缓慢增加。目前测值在-0.09～0.3 MPa之间，测值较小，表明坝踵被拉裂的可能性很小。

上下游方向（Y向）应力分析成果：除S511-CF所在部位混凝土表现为受压状态外，其余测点部位混凝土均处于受拉状态，目前测值在-0.10～0.87 MPa之间，在混凝土抗拉（压）的允许范围内变化。

左右岸方向（X向）成果：各部位测点混凝土均表现为拉应力。从测值过程线看，除S512-CF所在部位测值变化稳定，拉应力在2.38 MPa左右，其余各测点混凝土的拉应力在缓慢减小，目前量值较小，在0.14～0.19 MPa之间。该方向混凝土目前均表现为拉应力，测值在混凝土抗拉允许范围内变化。

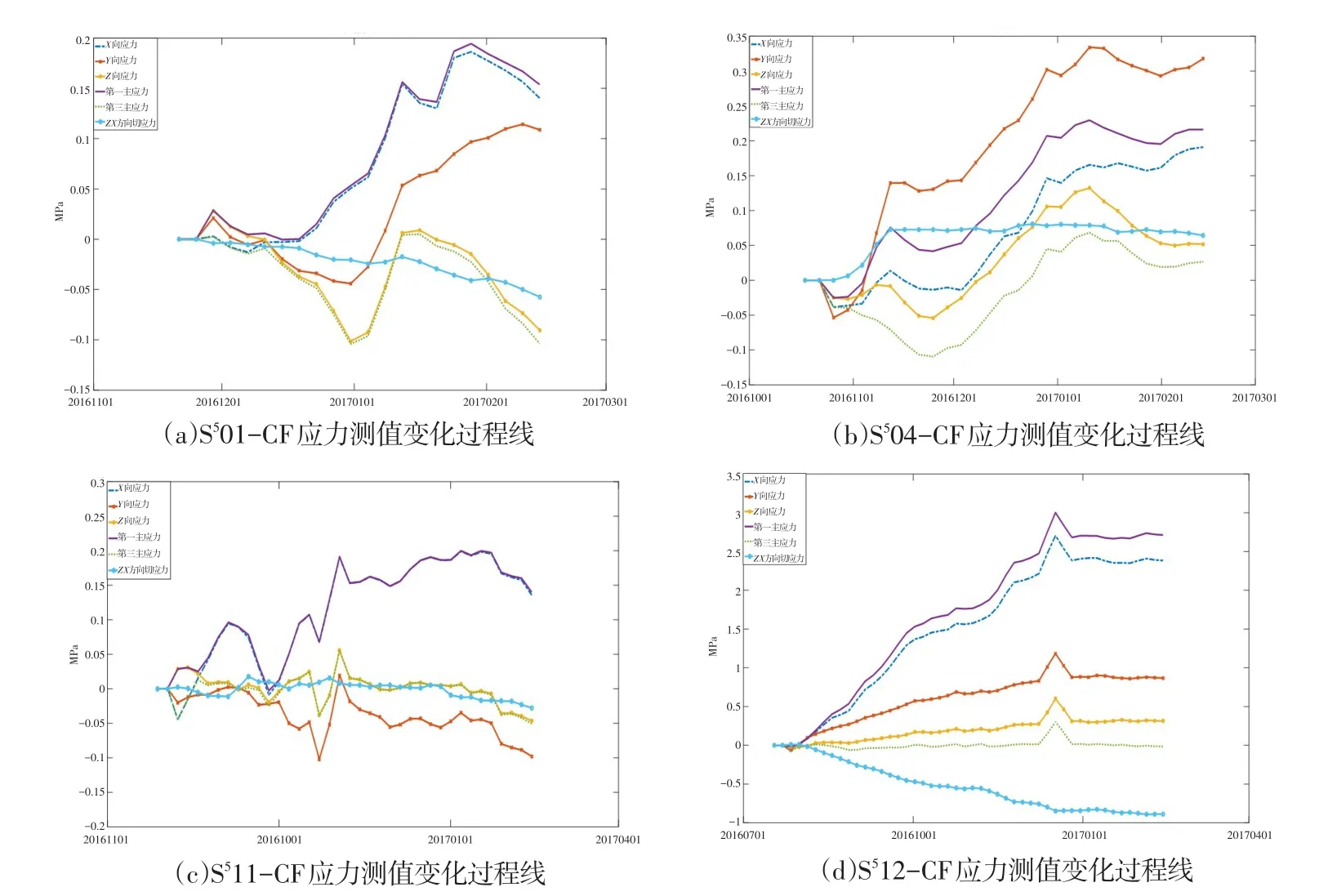
图4 五向应变计组所在部位混凝土应力测值过程线Fig.4 Graph of the concrete stress where the five-direction strain gauges embedded

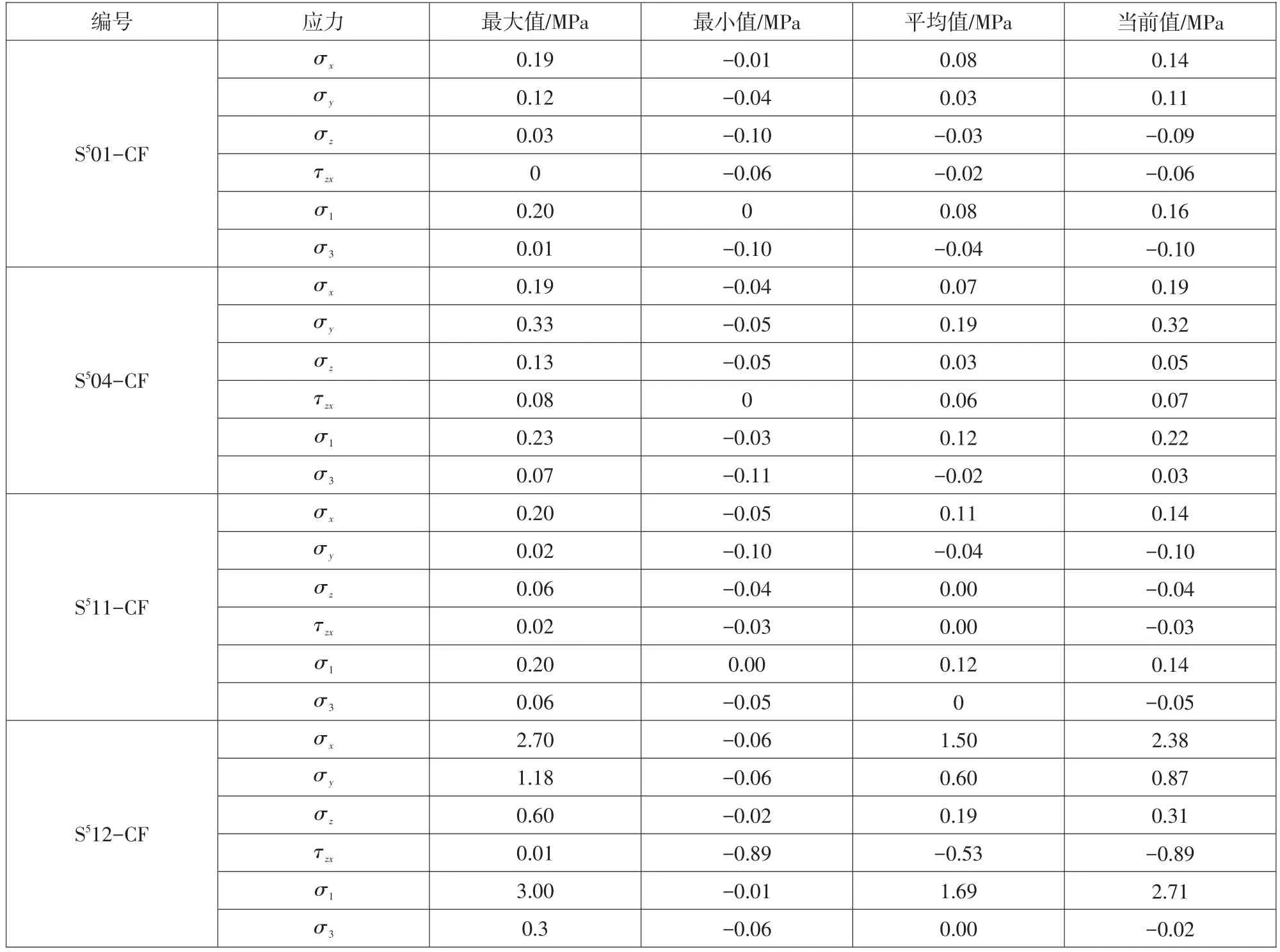
表2 混凝土应力特征值统计表Table 2 Statistics of the eigenvalues of concrete stress

4 结语

（1）通过采用变形法，应用MATLAB计算及绘图程序语言，对国内某工程厂房坝段埋设的五向应变计组的施工期监测资料进行了分析。监测分析发现，S512-CF所在部位混凝土的应力应变测值较大，但应力测值尚在允许范围内，目前已趋于稳定状态，混凝土结构物的运行状况正常。

（2）分析认为，各应变计组的应变不平衡性较大，无应力计测值中包含温度应变，以及应力计算时缺少施工期混凝土徐变试验结果，这些因素对混凝土应力的计算精度均会产生一定影响，需做进一步的改进，以提高计算混凝土应力应变的准确性。 ■

[1]武先伟.高拱坝应力应变监测关键技术问题研究及其应用[D].宜昌：三峡大学,2014.

[2]DL/T 5209-2005,混凝土坝安全监测资料整编规程[S].

[3]朱伯芳.混凝土的弹性模量、徐变度与应力松弛系数[J].水利学报,1985(9)：54-61.