基于工程长期运行监测的地下工程三维渗流场优化反演分析

倪绍虎，田 伟，赵毅锋，魏盛夏子，赵瑞存，郑海圣

（1.中国电建集团华东勘测设计研究院有限公司,浙江杭州，311122；2.浙江省抽水蓄能工程技术研究中心，浙江杭州，311122；3.华东天荒坪抽水蓄能有限责任公司，浙江湖州，313300）

0 引言

地下水的影响是地下工程设计中必须考虑的关键环节之一。一方面地下水通过物理力学作用软化岩体，改变其物理力学特性，另一方面也是结构主要荷载，直接关系到工程稳定及结构安全，渗流作用下隧洞突水突泥、内水外渗发生渗漏、外水渗漏等诸多问题，均为地下水渗流引起。因此，当地下水较丰富时，为全面了解地下水分布及其对工程的影响，通常需要进行三维渗流场分析[1-2]。

地下水渗流分析最为关键的环节是通过大量的工程地质、水文地质探查、勘测，查明地下水的发育程度、空间分布特征及区域岩体的渗透性。通常采用现场地质钻孔进行原位试验，这些现场试验获得的结果能较好地反映试验区渗透特性。然而岩土介质是十分复杂的非均一介质，试验成果往往离散性较强，代表性较差。同时原位试验也需要耗费大量人力和物力，因此，利用原位观测、监测获取的地下水数据信息进行渗流场反分析，反演获得各渗透分区渗透系数、渗流场分布、涌水量、渗漏量等指标，具有很好的工程实用性和应用价值。

反演分析方法已广泛应用于工程渗流分析中。朱岳明等[3]通过优化算法反演分析了岩体渗透系数张量。刘先珊等[4]提出模拟退火算法神经网络，对大坝渗流场进行了反分析。盛金昌等[5]运用序列二次优化方法，反演了工程区域的天然渗流场。谢红强等[6]结合工程区域水文地质资料，反演分析了岩体各向异性渗流场。张璇等[7]采用正交设计参数样本，利用遗传神经网络反演了工程区域的初始渗流场。段斌等[8]采用二次规划反演，对天然渗流场进行了反演分析。魏进兵等[9]采用BP网络对滑坡体进行了非饱和渗流反演。

然而岩土工程反演多维多极值问题的求解是一个极其复杂的问题。为了得到理想可靠的渗流反演结果，对软、硬件两方面都有相当高的要求，需要一种高效适用的数学或仿生智能优化方法，能够实现对多参数多维问题的多目标优化快速搜索。基于此，运用有限单元法进行三维渗流场分析，提出采用粒子群智能优化算法进行复杂三维渗流场优化反演分析，显著提高反演计算效率和可靠性，可有效应用于地下岩土工程渗流分析、渗流控制及水文地质条件评价中。

1 三维渗流场优化反演分析

1.1 等效连续介质渗流分析的基本前提

严格来讲，岩体是非连续介质，其渗流问题多属于裂隙渗流问题，完整的岩块渗透性极低，岩体渗流主要受其内部结构面和微裂隙控制。但裂隙网络渗流比较复杂，裂隙网络分布及参数基本不可能准确获得。因此，通常在满足一定条件时，可采用等效连续介质的方法将裂隙岩体渗流概化为连续介质模型。对于岩体渗透性表征单元体存在且相对计算模型很小时，采用等效连续介质渗流模型是可行的、高效的[10-11]，同时也完全能满足工程需要。

渗流问题能否视为等效连续介质渗流问题的关键在于分析域的渗流表征单元体积，即尺寸效应。尺寸效应是裂隙岩体的典型特征，如图1所示。岩体中的微裂纹、节理、裂隙等不连续结构面的存在，使不同试件尺寸以及不同结构面发育程度的岩体的特性各异。不同研究范畴的裂隙岩体的表征单元体积不同，其物理力学特性和渗透特性有不同的表征单元体积，分别代表岩体力学特性的尺寸效应和渗透特性的尺寸效应，称渗透特性的表征单元体积为渗透表征单元体积（permeability representative element volume，PREV），如图2所示。土体等孔隙介质中固体颗粒间的孔隙很小，其PREV非常小，渗流分析时通常可作为连续介质考虑。而裂隙岩体不同，其空隙结构主要为孔隙较大的裂隙网络，其PREV一般较大甚至不存在，因此，在多数情况下不能等效为连续介质，而应按照非连续介质考虑，即使在某些情况下可以按等效连续介质考虑，也必须考虑其渗透各向异性。

WEI Z Q等人[12-13]提出了裂隙岩体PREV估算方法，当模型尺寸大于10倍任意节理的隙间距St时，裂隙岩体的渗透性趋于稳定；当模型尺寸大于50倍任意节理的隙间距St时，岩体的渗透性变化很小。单组裂隙PREV可表示为：

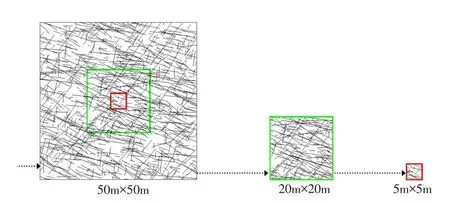
图1 裂隙岩体尺寸效应示意图Fig.1 Size effect of the fractured rock

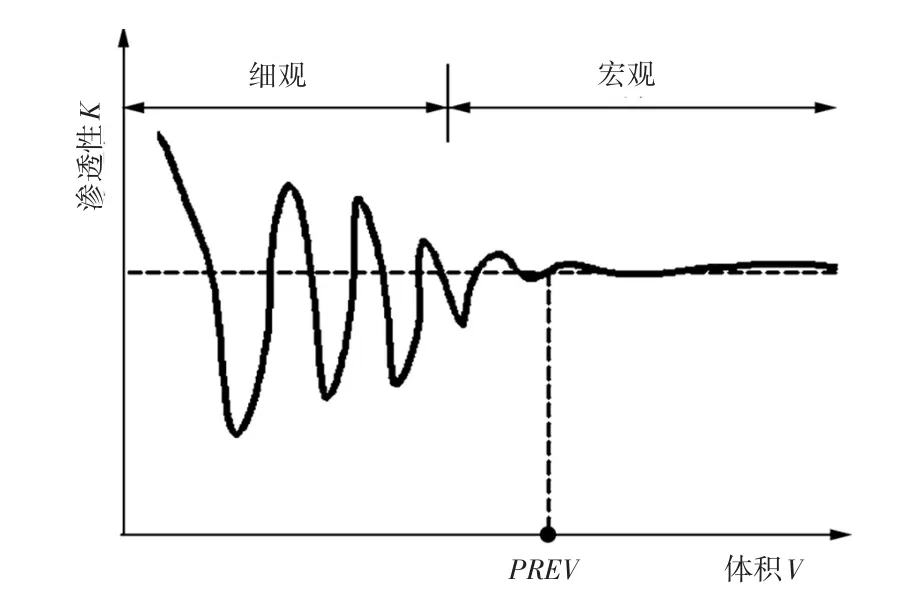
图2 裂隙岩体渗透表征单元体积示意图Fig.2 Volume of the permeability representative element of the fractured rock mass

式中，St为单组裂隙平均间距。对于几何特性和分布不同的多组裂隙，可用多组裂隙的平均间距Sa0代替St，并可表示为：

在裂隙岩体PREV存在且远小于研究区域尺寸时，可以等效为连续介质考虑，通过裂隙岩体的渗透张量来描述裂隙岩体的渗透各向异性及裂隙网络的水力学行为。若表征单元体不存在或过大，可考虑将研究区域进行渗透性分区，再确定分区岩体的渗透性表征单元体。若表征单元体确实不存在或太大，则不能采用等效连续介质模型。

1.2 渗流有限单元法基本原理

采用等效连续介质渗流模型进行三维稳定渗流场反演分析，计算方法采用有限单元法。对于稳态渗流问题，其有限单元法基本方程可表示为：

式中，[K]为渗透传导矩阵；{h}为节点势列阵；{F}为节点流量列阵。

1.3 渗流优化反演分析方法

岩体渗流反分析通常分为直接法和间接法两大类。直接法要求实测数据较为完备且准确性较高，应用较少。间接法则利用正问题解的适定性，通过数学方法将计算值逐步逼近观测值，运用广泛。优化反演时，研究区域内测点的计算值与实测值的误差，表示为：

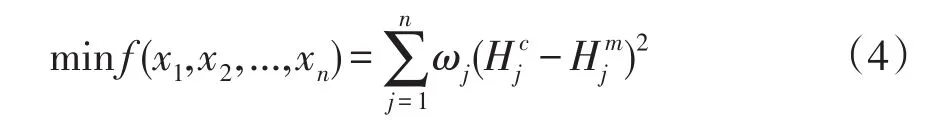
式中：n为测点总数；xi(i=1,2,...,n)为一组反映岩体渗流场的水文地质参数，如导水系数、给水度等多种初始参数；ωj为第 j测点的权重因子为第 j测点处的水头（流量）计算值；为第 j测点处的现场水头（流量）监测值。

2 粒子群优化算法

优化反演需借助数学方法，即优化算法，采用改进的粒子群优化算法进行渗流场优化反演分析。算法基于种群的全局搜索策略，根据粒子自身速度指导优化搜索，粒子群根据记忆调整搜索策略，以实现路径最优。

粒子群算法中，各粒子均是搜索空间中的一个解。采用“群体”和“进化”的概念，依据粒子个体的适应值大小进行操作。根据粒子自身的飞行经验和同伴粒子的飞行经验，调整粒子飞行策略和路径。每个粒子通过飞行过程的最好位置以及粒子群体经历过的最好位置，不断更新自己调整飞行轨迹，从而产生新一代群体，再进入下一次飞行。对于第k次迭代，每一个粒子按下式更新：

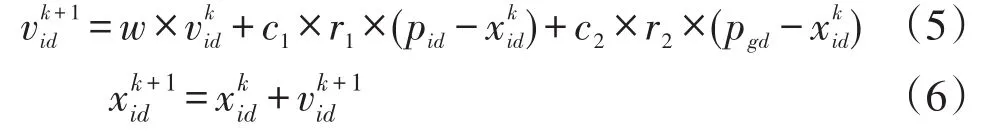
式中：i=1,2,…,M，M为群体中粒子的总数；w为惯性权重系数；为第k次迭代粒子i飞行速度矢量的第d维分量；为第k次迭代粒子i位置矢量的第d维分量；pid为粒子i个体最好位置的第d维分量；pgd为群体最好位置的第d维分量；c1、c2为学习因子，通常取[0,4]的两个定常数，推荐取为c1=c2=2.0；r1、r2为[0,1]的相互独立的随机数。

3 工程运用

将上文所述的粒子群优化算法运用于浙江省天荒坪一级抽水蓄能电站长期运行期的三维渗流场优化反演分析中。

3.1 工程概况及水文地质条件

天荒坪抽水蓄能电站位于浙江省安吉县天荒坪镇境内，距离杭州57 km，距离上海175 km，接近华东电网的负荷中心。电站枢纽主要由上水库、下水库、输水系统、地下厂房洞室群和开关站组成，安装6台300 MW的抽水蓄能机组，总装机容量1 800 MW。

输水系统由上水库进/出水口、斜井、混凝土岔管、钢支管、尾水隧洞及下水库进/出水口等组成，引水隧洞采用一洞三机布置型式，尾水隧洞采用一洞一机布置型式。

输水系统皆处于地下水位线以下。由于沿线地形陡峻，地下水补给条件差～较差，岩体完整～较完整，赋水性差，开挖过程中初始地下水出露点不多见，沿结构面渗出，多呈滴水，局部可见小股线流，流量小，初始洞内除几处出水点外，部分洞段潮湿，大部分洞段干燥。

输水系统沿线基岩为凝灰岩，后期侵入花岗斑岩及煌斑岩脉。围岩完整性好，岩质坚硬。根据工程建设期地下岩体灌前压水试验数据，围岩渗透系数反演范围为K=1.0×10-9～1.0×10-7m/s。根据地下岩体灌前压水试验数据，固结灌浆和灌浆帷幕渗透系数反演范围为K=1.0×10-10～1.0×10-8m/s。

电站自1998年充水发电以来，电站运行安全。运行近20年，获得了大量地下水、渗漏量等实测数据和资料。利用这些实测数据，反演工程区域三维渗流场，对地下水分布、渗控效应、帷幕防渗效果评价、修复方案制订等有重要参考意义。

3.2 三维渗流场优化反演分析模型

三维渗流场反演计算区域选取上库到下库范围，包含引水发电系统地下洞室群所有建筑物。X轴与引水钢管轴线平行，指向下游为正；Y轴与引水钢管轴线垂直，从1号钢管指向6号钢管为正；Z轴与大地坐标重合，指向上为正。整体模型范围：X方向从-615.61到472.14共1 087.75 m；Y方向从-266.70到347.20共613.90 m；Z方向从64.94到1 049.59共984.65 m。模型采用空间8节点等参单元，共划分等参单元230 732个。计算模型如图3和图4所示。

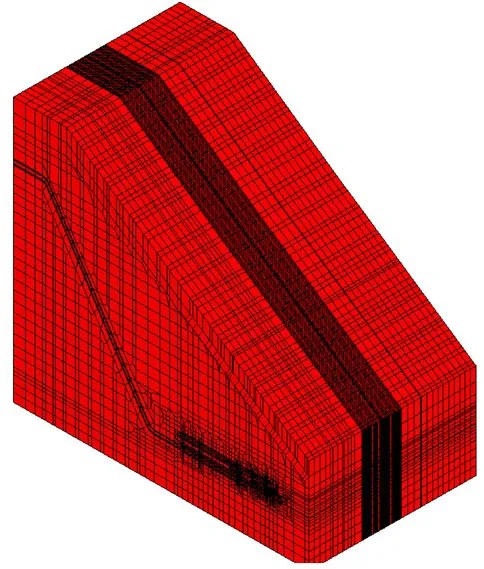
图3 三维渗流反演分析有限元计算模型Fig.3 FEM model of 3D seepage back analysis

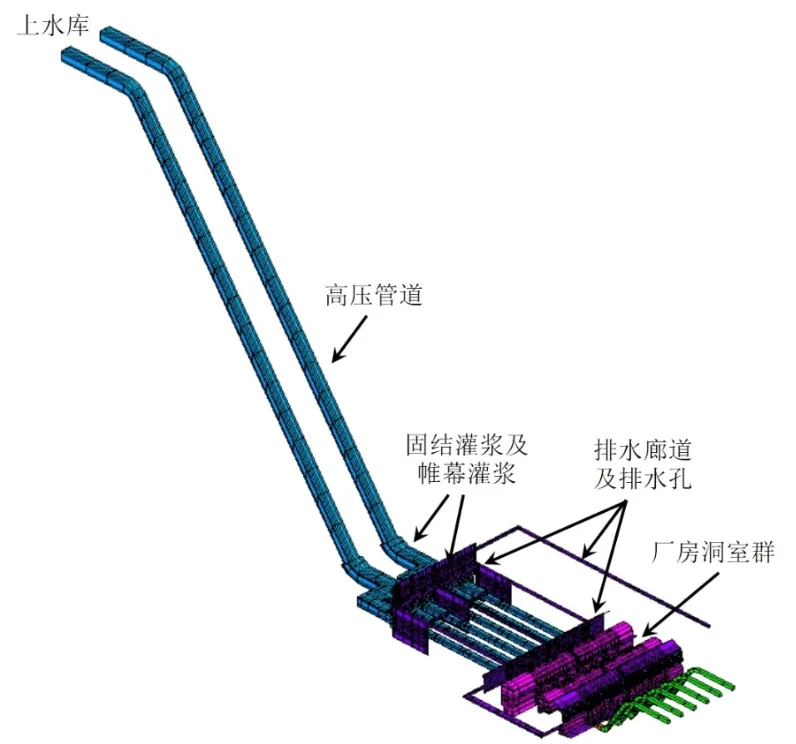
图4 三维渗流反演分析地下洞室有限元计算模型Fig.4 FEM model of the underground caverns and tunnels in 3D seepage back analysis

3.3 三维渗流场优化反演分析结果

以地下水位测孔、平硐量水堰作为反演主要依据。通过100代例子反演，达到收敛标准。反演所得上下部围岩和固结灌浆渗透系数如表1所示，反演结果均在钻孔实测范围之内。从渗透系数量值大小上看，上部围岩最大，下部围岩次之，固结灌浆最小。结合地质勘察资料，在斜井以上部位发育多条断层，从宏观上来看，上部围岩渗透系数要比下部围岩大。固结灌浆提高围岩整体性的同时也降低了透水性，因而其渗透系数理论上要比围岩小。因此，反演的参数大小关系合理。

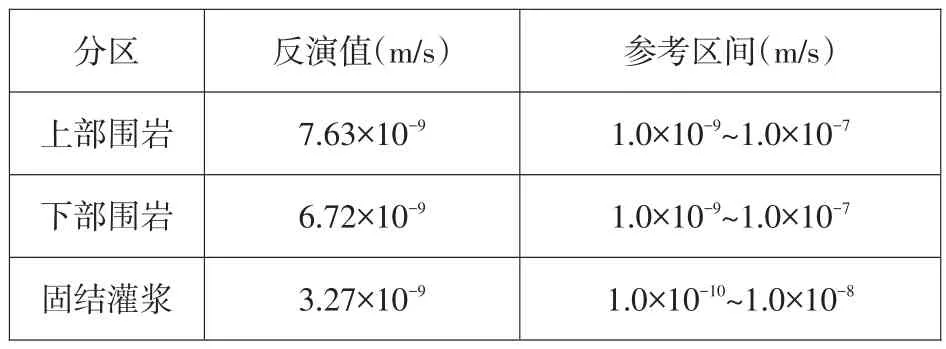
表1 反演渗透系数表Table 1 Permeability coefficients in the back analysis

反演各水位测孔相对误差均在5%以内，反演结果合理。个别水位测孔误差较大，主要原因是复杂的地质条件，各种断层、节理等的分布对渗流场都会产生影响，是导致误差的一个重要原因。

工程区大范围渗流等水头线光滑，从上库到下库呈现逐渐减小的趋势。在上下部围岩交界面上，渗流等水头线出现微小折线，反映了两种围岩渗透系数的差异。在输水系统高压管道附近，渗流等水头线出现了上壅的趋势，反映了斜井内水外渗导致上体地下水位壅高的效应。由于山体陡峭，上体地下水位和下库水位相对都较高，厂房区位于自由水面之下，这与实际观测中厂房顶拱渗水相吻合。在岔管和钢衬接头处，渗流等水头线密集，说明该处渗流坡降大，渗透荷载消散较快。而在钢管段和厂房段，渗流等水头线稀疏，说明该处渗流坡降较小，这说明灌浆帷幕和排水孔幕很好地阻止了斜井的地下水渗漏到高压岔管段和厂房段，其阻排水效果显著。在厂区完善的排水廊道、排水孔和灌浆帷幕的排水、阻水作用下，整个地下厂房周围渗透水头很小。

总体来看，反演结果与实测资料相差不大，反演所得渗流场可以反映工程区大范围的实际地下水分布和渗流状态，此渗流反演结果可用于指导工程运行、维护和检修。

4 结语

基于工程区域长期实测水位、流量数据，采用粒子群智能优化算法进行渗流场优化反演，显著提高了复杂三维渗流场的反演分析效率和计算精度，应用于实际工程的三维渗流场反演分析中，较好地解决了复杂三维渗流场反演难题。

（1）对于渗透性表征单元体存在且相对计算模型较小的岩土工程渗流问题，可按等效连续介质模型进行渗流分析。

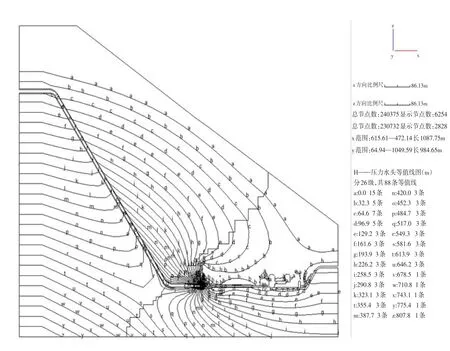
图5 运行期输水发电系统反演三维渗流场压力水头分布Fig.5 Distribution of water head along water transmission and power system in 3D seepage field back analysis

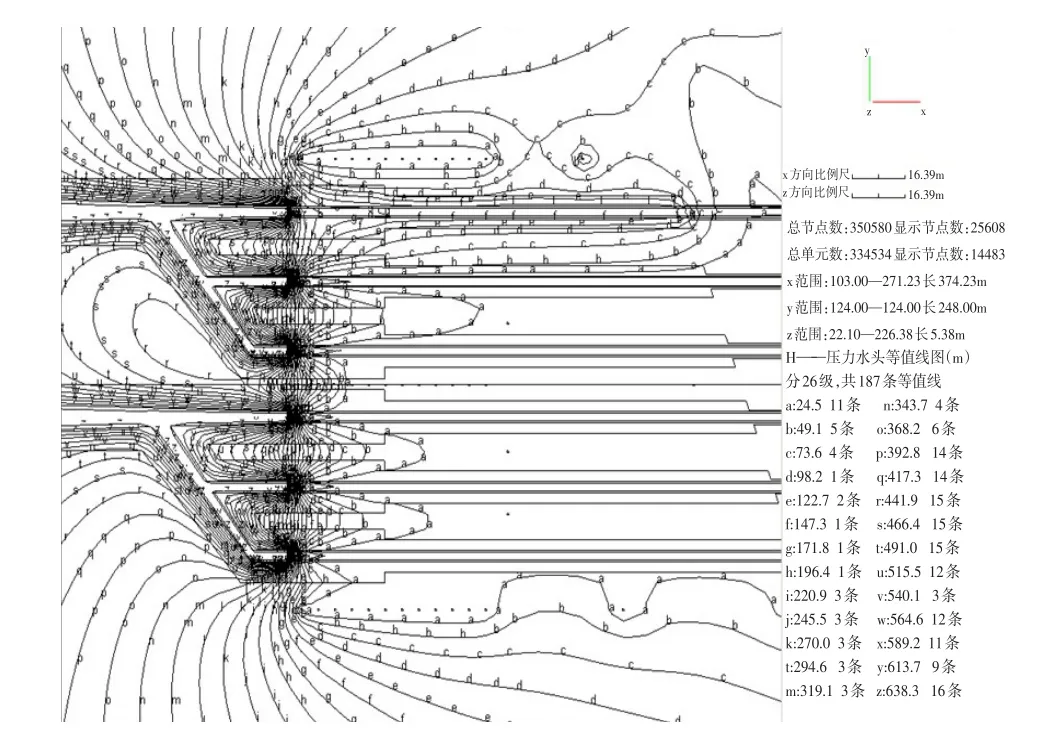
图6 运行期高压管道区域反演三维渗流场压力水头分布Fig.6 Distribution of water head around the high pressure bifurcated tunnel during operation in 3D seepage field back analysis

（2）基于连续介质的有限单元法，采用粒子群优化算法进行渗流场反演，对于边界条件能相对准确确定的问题，通过文中所述优化反演分析方法，反演获得的参数及渗流场分布是比较准确和可靠的，反演精度基本能满足工程需要。

（3）三维渗流场反演分析方法可有效应用在岩土工程地下水分析中，但对实测数据准确性、合理性要求较高。实测数据信息越准确，反演结果越精确，同时实测数据信息越多，反演结果也越可信。

（4）反演分析方法除应用于地下岩土工程渗流反演分析外，也可应用于大坝、边坡等工程渗流反演分析中。 ■

[1]杜延龄,许国安.渗流分析的有限单元法和电网络法[M].北京：水利电力出版社,1992：1-2.

[2]张有天.岩石水力学与工程[M].北京：中国水利水电出版社,2005：8-25.

[3]朱岳明,张燎军,吴愔.裂隙岩体渗透系数张量的反演分析[J].岩石力学与工程学报,1997,16(5)：461-470.

[4]刘先珊,周创兵,张立君.基于模拟退火的Gauss-Newton算法的神经网络在渗流反分析中的应用[J].岩土力学,2005,26(3)：404-414.

[5]盛金昌,速宝玉,詹美礼.三维天然渗流场反演分析及工程应用[J].岩石力学与工程学报,2003,22(2)：203-207.

[6]谢红强,何江达,符文熹,等.大岗山水电站厂坝区各向异性渗流场反演分析[J].四川大学学报（工程科学版）,2007,39(增)：132-135.

[7]张璇,李毅,罗琳,等.基于遗传神经网络的坝区初始渗流场反分析[J].水电能源科学,2012,30(12)：74-77.

[8]段斌,张林,何江达,等.复杂裂隙岩体天然渗流场反演分析[J].水力发电学报,2012,31(3)：188-198.

[9]魏进兵,邓建辉,高春玉,等.三峡库区泄滩滑坡非饱和渗流分析及渗透系数反演[J].岩土力学,2008,29(8)：2262-2266.

[10]Duncan C Wyllie,Christopher W Mah.Rock Slope Engineering(4th edition)[M].London：Spon Press,2005：74-78.

[11]倪绍虎,何世海,汪小刚,等.裂隙岩体水力学特性研究[J].岩石力学与工程学报,2012,31(3),488-498.

[12]WEI Z Q，HUDSON J A.Permeability of jointed rock masses[C].Proceeding of ISRM Symposium：Rock Mechanics and Power Plants,Madrid：Romana，1988：613-625.

[13]WEI Z Q，EGGER P，DECOEUDRES F.Permeability predictions for jointed rock masses[J].International Journal of Rock Mechanics and Mining Sciences&Geomechanics Abstract，1995，32(3)：251-261.

[14]周志芳,王锦国.裂隙介质水动力学[M].北京：水利电力出版社,2004：241-245.

[15]Kennedy J,Eberhart R C.Particle swarm optimization[C].Conf.on Neural NetworksⅣ,1995：1942-1948.

[16]Shi Y H,Eberhat R C.Parameter selection in particle swarm optimization[J].In Evolutionary ProgrammingⅦ：1998：591-600.

[17]Shi Y H,Eberhat R C.A modified particle swarm optimizer[C].Proceedings of the IEEE International Conference on Evolutionary Computation,1998：591-600.

[18]高玮.基于粒子群优化的岩土工程反分析研究[J].岩土力学，2006,27(5)：795-798.

[19]倪绍虎,肖明.基于围岩松动圈的地下工程参数场位移反分析[J].岩石力学与工程学报,2009,28(7)：1439-1446.

[20]倪绍虎,肖明,王继伟.改进粒子群算法在地下工程反分析中的运用[J].武汉大学学报（工学版）,2009,42(6)：326-330.

[21]常晓林,喻胜春,马刚,等.基于粒子迁徙的粒子群优化算法及其在岩土工程中的应用[J].岩土力学,2011,32(4)：1077-1082.

[22]倪绍虎,肖明,何世海,等.地下工程并行优化反演分析及算例验证[J].岩石力学与工程学报,2013,32(3)：501-511.