一个二重积分的计算方法探讨

景慧丽，屈 娜

(火箭军工程大学 理学院, 陕西 西安 710025)

0 引言

二重积分是多元函数积分学中最基本、最重要的概念之一，能正确地计算二重积分是学员学习多元函数积分学必须掌握的基本能力之一，因为三重积分和两类曲面积分的计算都要借助于二重积分，平面曲线积分通过格林公式也可转化成二重积分，可以说二重积分的计算是多元积分学的基础.计算二重积分的基本方法是把二重积分转化为二次积分(即两次定积分)[1]240，当然有时候也可以利用对称性来简化二重积分的计算，有时候还需要选择恰当坐标系和积分次序，而另一方面，有的二重积分又可以用多种方法来计算.因此二重积分的计算问题就显得比较开放，这种开放性又可以用来培养学员的发散思维.所以，在教学中教员可以通过二重积分的计算来培养学员的发散思维.本文针对一个二重积分的计算问题进行探讨，提出5种计算方法，进而培养学员的发散思维.

1 转化为直角坐标系下先对y后对x的二次积分

注2：解法1是最基本也是最常用方法，大部分初学者首先考虑的就是这种方法，这类方法的关键和核心是二次积分中两个定积分的积分限的确定.可以利用“穿越定限法”来确定积分限，“穿越定限法”要领是“后积先定限，限内画条线，先交下限写，后交上限见”.意思是，如果积分区域D是X-型域，就要先确定x的积分限，然后再确定y的积分限，y的积分限的确定方法是：用垂直于x轴的直线从下向上穿过区域，直线与区域的边界先交的就是y的下限，后交的就是y的上限；如果积分区域D是Y-型域，就要先确定y的积分限，然后再确定x的积分限，x的积分限的确定方法是：用垂直于y轴的直线从左向右穿过区域，直线与区域的边界先交的就是x的下限，后交的就是x的上限.这种“穿越定限法”思想可以完全推广到三重积分.

注3:化二重积分为二次积分时，不管选择哪一种积分次序，内层和外层的积分限都必须上限大于下限.一般情况下，内层积分的积分限可以依赖于外层积分的积分变量，但外层积分限必须是确定的，即绝不能依赖于内层积分变量[2]216.

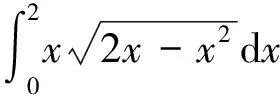
2 转化为极坐标系下先对ρ后对θ的二次积分

注5:利用极坐标系(ρ,θ)计算二重积分也是一种常用的非常重要的方法.在极坐标系下也是把二重积分转化为二次积分来计算的，并且往往是化为先对ρ、后对θ的二次积分，二次积分的积分限的确定方法也是“穿越定限法”，只是这里“限内画条线”是从极点出发穿过区域画线.

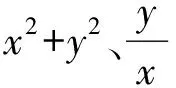
注7:解法1和解法2在计算定积分时，都应用了定积分的对称性来简化计算，其实对二重积分也可以利用对称性来简化计算.

3 先利用重积分的线性性质再利用对称性最后利用极坐标系化为二次积分

因此

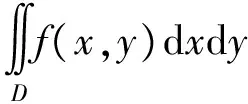
1)积分区域D关于坐标轴具有对称性；

2)被积函数f(x,y)关于变量x或y具有奇偶性；

3)被积函数的奇偶性要与积分区域的对称性“相匹配”.

“相匹配”是指如果积分域D关于x轴对称，被积函数f(x,y)则要关于变量y具有奇偶性.如果积分域D关于y轴对称，被积函数f(x,y)则要关于变量x具有奇偶性.只要上述三个条件有一个不满足，就不能应用对称性来简化二重积分的计算.

注9:利用对称性计算二重积分的思想可以完全推广到三重积分、第一类曲线积分和第一类曲面积分，对三重积分和曲面积分来说，积分域要关于坐标面具有对称性.

4 先利用重积分的线性性质再利用对称性最后利用直角坐标系化为二次积分

5 利用形心公式

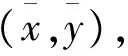
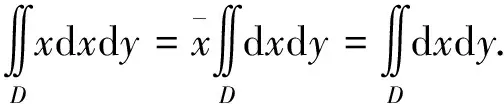
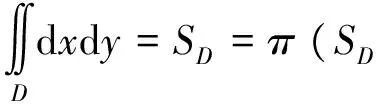
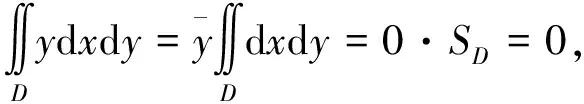
注10:也可以利用形心公式计算三重积分、第一类曲线积分、第一类曲面积分.

6 结语

由上述计算方法可以看出，对一道题目的解法往往有不同的思路，知识点之间表面上看是相互独立的，实际上它们具有一定的联系.另外，《高等数学》课程中很多题目都可以用多种思路和方法来求解，教员在应用这类一题多解的题目组织教学时，必须以学员为本，鼓励学员积极参与教学活动，鼓励学员敢于标新立异，勇于提出问题、开展交流和讨论，这样才有利于学员突破思维的局限性，培养学员的发散思维和综合能力[3]26.

[1] 同济大学数学系.高等数学(下)[M].7版.北京：高等教育出版社,2014.

[2] 崔荣泉.高等数学重点内容重点题[M].1版.西安：西安交通大学出版社，2004.

[3] 景慧丽，杨宝珍，刘 华，等.一个不等式的证明方法探讨[J].重庆工商大学学报(自然科学版)，2014,31(8).