基于矩阵的多粒度粗糙集上、下近似表示

汪小燕，彭 刚，沈家兰，申元霞

（安徽工业大学 计算机科学与技术学院，安徽 马鞍山 243032）

粗糙集理论[1]是波兰学者Pawlak教授于1982年提出的分析不完整、不精确知识的数学工具。经过几十年来的发展，与粗糙集相关的研究已经取得了巨大的进步，并成功地运用于数据挖掘、神经网络、智能计算等领域。

多粒度粗糙集[2-9]是近些年粗糙集研究的一个重要方向，是Pawlak粗糙集理论的发展，它利用多个粒度空间对目标概念进行近似逼近，使得目标概念的表示精度进一步提高，并可以与其他处理不确定知识的理论结合。多粒度粗糙集模型中的关键理论是上、下近似，计算上、下近似对获取决策知识具有重要的意义。一般上、下近似求取是根据定义中提供的公式来计算，计算过程不直观且容易出错。矩阵在粗糙集中应用广泛，如：属性约简[10]，属性值分类[11]等。笔者提出多粒度二进制矩阵，利用矩阵获取集合的上、下近似，计算简单、直观，而且很容易计算关于不同粒度组合的上、下近似。

1 基本概念

粒计算是近些年发展起来的一门学科，钱宇华等学者将粗糙集理论进行扩展，打破传统的单粒度结构，采用多个知识粒近似表示目标概念，提出了多粒度粗糙集模型，包括乐观多粒度粗糙集和悲观多粒度粗糙集。目前，多粒度粗糙集已成为研究粒计算的重要工具。

定义 1[2]设信息系统 IS＝＜U，AT，V，f＞，A={A1，A2，…，Am}是 AT 的 m 个属性子集，∀X⊆U，则 X 关于属性子集A的乐观多粒度粗糙集的下、上近似定义为

定义 2[2]设信息系统 IS＝＜U，AT，V，f＞，A={A1，A2，…，Am}是 AT 的 m 个属性子集，∀X⊆U，则 X 关于属性子集A的悲观多粒度粗糙集的下、上近似定义为

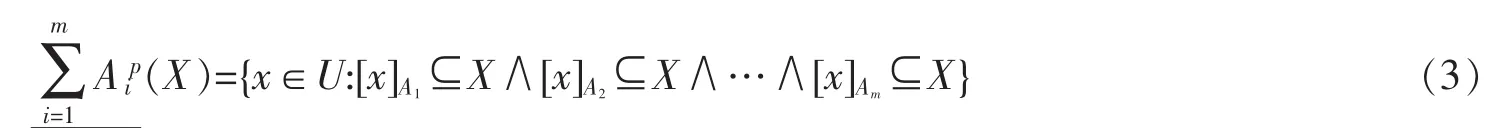
2 多粒度粗糙集二进制矩阵

定义 3设 S＝＜U，AT，V，f＞是一个信息系统，其中 A1，A2，…，Am⊆AT，D 为决策属性，A={A1，A2，…，Am}，U/D={Y1，Y2，…，Yn}，则多粒度粗糙集二进制矩阵 M={mij}定义为

根据定义1、定义2中乐（悲）观多粒度粗糙集的上、下近似定义，结合多粒度粗糙集二进制矩阵，可得如下推论。

推论1M是多粒度粗糙集二进制矩阵，A是所有条件属性粒度集合，若某个对象x∈U与某个决策类Y∈U/D所对应的元素mij包含1，则

推论2 多粒度粗糙集二进制矩阵M中，A是所有条件属性粒度集合，对Y∈U/D，则Y∈U/D列包含1的元素mij所对应的对象x}。

推论3M是多粒度粗糙集二进制矩阵，A是所有条件属性粒度集合，若某个对象x∈U与某个决策类Y∈U/D所对应的元素mij不包含1，则

推论4M是多粒度粗糙集二进制矩阵，A是所有条件属性粒度集合，U/D＝{Y1，Y2}，若某个对象x∈U与决策类Y2所对应的元素mij不包含1，则

推论5M是多粒度粗糙集二进制矩阵，A是所有条件属性粒度集合，U/D＝{Y1，Y2}，则U：Y2列不包含1的元素mij所对应的对象x}。

推论6M是多粒度粗糙集二进制矩阵，A是所有条件属性粒度集合，若某个对象x∈U与某个决策类Y∈U/D所对应的元素mij包含m个1，则

推论7多粒度粗糙集二进制矩阵M中，A是所有条件属性粒度集合，对Y∈U/D，则Y∈U/D列包含m个1的元素mij所对应的对象x}。

推论8M是多粒度粗糙集二进制矩阵，A是所有条件属性粒度集合，若某个对象x∈U与某个决策类Y∈U/D所对应的元素mij包含0，则

推论9M是多粒度粗糙集二进制矩阵，A是所有条件属性粒度集合，U/D＝{Y1，Y2}，若某个对象x∈U与决策类Y2所对应的元素mij含有0，则U：Y2列包含0的元素mij所对应的对象x}。

推论10M是多粒度粗糙集二进制矩阵，A是所有条件属性粒度集合，U/D＝{Y1，Y2}，则

3 实例分析

设决策系统 IS＝＜U，AT，V，f＞，其中对象集 U={x1，x2，…，x9}，条件属性 AT={c1，c2，c3，c4}，d 为决策属性，见表 1。由表 1 知 U/IND（{d}）={D1，D2}，其中 D1＝{x1，x3，x5，x7，x9}，D2＝{x2，x4，x6，x8}，设决策信息系统的属性子集族如下：A＝{A1，A2，A3}={{c1，c2，}，{c2，c3}，{c3，c4}}。

根据定义3建立多粒度粗糙集二进制矩阵见表2。

表1 决策系统

表2 二进制矩阵

由表2可获得多粒度粗糙集的下近似、上近似分别为

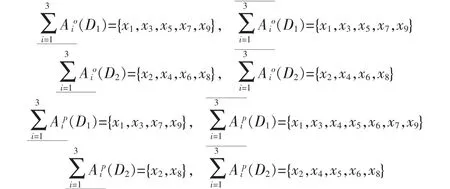
当粒度组合B={A1，A3}时，计算B关于D1，D2下近似、上近似时，只需要关注表2中每个mij的第一和第三个元素，现针对悲观多粒度粗糙集，以决策类D1为例。

4 结语

研究了多粒度粗糙集的上、下近似计算，提出了多粒度粗糙集二进制矩阵，该矩阵反映了不同粒度分类是否包含于决策类情况，根据矩阵元素值可确定相应对象是否属于上、下近似，也可以快速计算不同粒度组合的上、下近似。并通过实例证明了用矩阵表达上、下近似的有效性。

[1]PAWLAK Z.Rough sets[J].International Journal of Computer and Information Science，1982，11（5）：341-356.

[2]QIAN Yuhua，LIANG Jiye，YAO Yiyu，et al.MGRS：A multi-granulation rough set[J].Information Sciences，2010，180（6）：949-970.

[3]QIAN Yuhua，LIANG Jiye，DANG Chunying.Incomplete multi-granulation rough set[J].IEEE Transaction on SystemsManand Cybernetics：Part A，2010，40（2）：420-431.

[4]QIAN Y，LI S，LIANG J，et al.Pessimistic rough set based decisions：A multi-granulation fusion strategy[J].Information Sciences An International Journal，2014，264（6）：196－210.

[5]LIN Guoping，QIAN Yuhua，LIANG Jiye.NMGRS：Neighborhood-based multi-granulation rough sets[J].International Journal of Approximate Reasoning，2012，53（7）：1080－1093.

[6]YANG Y，SONG X，CHEN Z，et al.Multi-granulation Rough sets in incomplete information system[J].International Journal of Machine Learning&Cybernetics，2012，3（3）：223-232.

[7]XU Weihua，WANG Qiaorong，LUO Shuqun.Multi-granulation rough sets based on tolerance relations[J].Soft Computing，2013，17（7）：1241-1252.

[8]徐怡，杨宏健，纪霞.基于双重粒化准则的邻域多粒度粗糙集模型[J].控制与决策，2015，30（8）：1469-1478.

[9]沈家兰，汪小燕，申元霞.可变程度多粒度粗糙集[J].小型微型计算机系统，2016，37（5）：1012-1016.

[10]汪小燕，程泽凯，申元霞.一种新的决策表属性值分类方法[J].苏州科技大学学报（自然科学版），2016，33（1）：61-64.

[11]汪小燕，杨思春，申元霞.变精度粗集模型的属性约简研究[J].计算机工程与应用，2015，51（14）：95-98.