ARIMA乘积季节模型在财政收入预测中的应用
蒋泽迪,程毛林
(苏州科技大学 数理学院,江苏 苏州 215009)
财政收入是衡量一个国家综合经济实力的重要指标之一,是国家制定相关经济政策的重要参考标准之一。对财政收入进行提前预测,有利于国家对未来的财政支出作出更加合理的预算,有利于国家制定与未来经济走势更加吻合的经济财政政策。国家财政季度收入是随着时间变化的一组随机数字序列,序列的整体变化呈现一定的规律性。因此,可以利用时间序列分析方法,对国家财政季度收入建立模型,利用建立的模型对未来的财政季度收入进行预测。
文中介绍了ARIMA乘积季节模型的基本知识,通过乘积季节模型对2004年第一季度至2016年第三季度的中国国家财政收入的季度数据进行建模,利用建立的模型对未来国家财政的季度收入进行预测,得到了未来国家财政季度收入的预测值,可以为国家制定合理的财政政策提供一定的参考。
1 ARIMA乘积季节模型结构与建模步骤
ARMA模型是由美国学者博克斯(George Box)和英国统计学家詹金斯(Gwilym Jenkins)共同建立的,也称为博克斯-詹金斯法,简称B-J法[1]。ARMA模型主要的组成部分包括了AR自回归模型与MA移动平均模型。
1.1 ARIMA 模型[2-3]结构
如果时间序列{Yt}是一个非平稳序列,通过对其进行d阶的差分运算,可以使其成为一个平稳的时间序列,那么就称{Yt}是一个具有阶p,d,q的求和自回归移动平均模型(ARIMA),模型的结构为

其中,▽d=(1-B)d,B 为后移算子,BYt=Yt-1,▽为差分运算,▽=(1-B),d 为差分阶数,Φ(B)=1-φ1B-φ2B2-…-φpBp,φ1,φ2,…,φp为自回归系数,Θ(B)=1-θ1B-θ2B2-…θqBq,θ1,θ2,…,θq为移动平均系数,E(εt)=0,Var(εt)=σt2,∀s≤t,E(Yt·εt)=0。
1.2 乘积季节ARIMA模型[4-5]结构
季节性时间序列的典型特征主要表现为在时间间隔为周期长度S的两个时间点上的随机变量有相对较

其中,D 是非负整数,▽SD=(1-BS)D,S 为季节性周期,D 为季节性差分阶数,▽S=1-BS为季节差分算子,U(BS)=1-Γ1BS-Γ2B2S-…-ΓPBPS,Γ1,Γ2,…,ΓP为季节自回归系数,V(BS)=1-H1BS-H2B2S-…-HQBQS,H1,H2,…,HQ为季节移动平均系数。
如果假设 εt是 ARIMA(p,d,q)模型,那么(1)式可以改写为

称(2)式为乘积季节 ARIMA 模型[2],其中,Φ(B)=1-φ1B-φ2B2-…-φpBp,U(BS)=1-Γ1BS-Γ2B2S-…-ΓPBPS,▽d=(1-B)d,▽SD=(1-BS)D,Θ(B)=1-θ1B-θ2B2-…θqBq,V(BS)=1-H1BS-H2B2S-…-HQBQS。
1.3 建模的基本步骤
(1)数据的获取:通过国家统计局网站获得2004年到2016年的国家财政收入的相关数据,经过计算和处理得到2004年第一季度到2016年第三季度的国家财政收入的季度数据,建立财政收入的时间序列;
(2)数据的平稳性检验及处理:利用ADF单位根检验的方法,对时间序列进行单位根检验,确定序列是否为平稳的时间序列,如果序列是非平稳的时间序列,则需要对原序列进行普通差分和季节差分[6],使其成为平稳的时间序列;
(3)模型的识别与建立:利用Box-Jenkins方法对乘积季节模型的阶数和模型的参数进行估计,通过观察时间序列的自相关、偏自相关函数的截尾或者拖尾特性,确定模型的参数p、d、P、D;
(4)模型的检验与诊断:对建立模型的残差序列进行诊断,判断残差序列是否是白噪声序列,如果残差序列不是白噪声序列,则需要对已经建立的模型进行修改,重新建立模型;
(5)预测:利用已经建立的模型对序列在未来某个时刻的取值进行预测,比较预测值与实际值的相对误差[7-8],如果相对误差小于5%,则说明已经建立的模型的预测精度比较高,对未来的预测值比较准确。强的相关性。如果时间序列{Yt}是一个季节性时间序列,关于{Yt}的季节性模型结构为
2 模型的建立
2.1 数据来源
文中的财政数据来源于中国国家统计局网站,通过对历年财政收入(亿元)的数据进行计算与处理,得到了2004年第一季度到2016年第三季度的中国国家财政收入的51个季度数据,将51个季度数据构成的时间序列记为X。
2.2 数据的平稳性检验和处理[9]
通过软件Eviews8.0对数据的平稳性进行检验,将由2004年第一季度到2016年第三季度的中国国家财政收入的51个季度数据所构成的时间序列X导入到Eviews8.0[10-11]中,对序列X做对数处理,记为Y=log(X),生成新的序列Y,对序列Y作出时间序列折线图(图1)。通过对Y序列折线图的观察,可以发现序列Y具有趋势性和季节性波动。采用ADF单位根检验的方法对序列Y进行平稳性检验(图2),通过观察可以发现,检验t统计量的值为-2.729 691,大于显著性水平为5%的临界值-2.928 142。因此,认为序列Y存在着单位根,是非平稳序列。

图1 Y序列的时间序列折线图
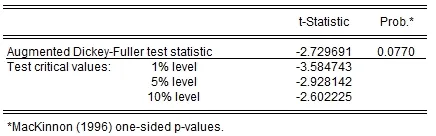
图2 Y序列的ADF单位根检验结果
所以,下面对序列Y做一阶差分处理,记为DY,对DY采用ADF单位根检验的方法进行检验,如图3。可以观察到t统计量的值为-3.210 999,小于显著性水平在5%的临界值-2.928 142,对应的概率为0.025 8,小于0.05,所以认为序列DY不存在单位根,是平稳的序列。通过对DY的自相关和偏自相关分析图(图4)的观察,可以发现,序列DY的趋势基本消除,但季节性依旧存在。
为了消除序列DY的季节性影响,需要对序列DY做一阶季节差分,记为SDY,绘制序列SDY的自相关和偏自相关分析图(图5)。由图观察发现,序列SDY的季节性基本消除,采用ADF单位根检验的方法对SDY进行单位根检验(图6)。从图6中可以看出,统计量t的值为-5.367 031,小于显著性水平1%的临界值-3.592 462,对应的概率为0.000 1,远远小于0.05,所以SDY是平稳序列。
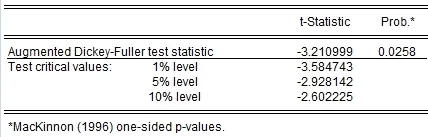
图3 序列DY的ADF单位根检验结果

图4 时间序列DY的自相关和偏自相关图

图5 时间序列SDY的自相关和偏自相关图

图6 序列SDY的ADF单位根检验结果
2.3 模型的识别与建立
笔者发现序列Y经过一阶差分和一阶季节差分之后,序列的周期性和季节性基本消除,所以d=1,D=1。由图5可以知道,s=4的时候,偏自相关系数显著不为0,所以选择P=1。自相关系数显著不为0,所以选择Q=1,初步判断ARIMA乘积季节模型为(p,1,q)×(1,1,1)4。 根据对图 5 关于 SDY 的自相关和偏自相关图的观察,可以发现SDY的自相关和偏自相关图都是拖尾的,结合ARMA(p,q)模型定阶的基本原则,主要考虑的模型[12-13]为 ARIMA(4,1,4)×(1,1,1)4,ARIMA(4,1,3)×(1,1,1)4,ARIMA(3,1,3)×(1,1,1)4。 模型选择之后,就要对选择的模型的参数进行显著性检验,并且根据AIC准则选择最优模型。三个模型的参数估计结果分别如图7,图8和图9,比较三个模型的参数检验结果,可以发现模型 ARIMA(4,1,4)×(1,1,1)4为最优模型,AIC=-2.795 602为最小的,SC值也比较小,R2值达到了最大,所以选择第一个模型 ARIMA(4,1,4)×(1,1,1)4是合适的。

图 7 ARIMA(4,1,4)×(1,1,1)4
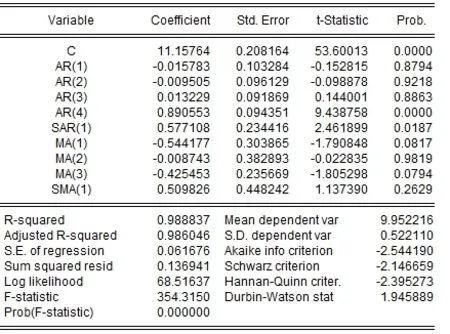
图 8 ARIMA(4,1,3)×(1,1,1)4

图 9 ARIMA(3,1,3)×(1,1,1)4
根据图 7 可以得到模型 ARIMA(4,1,4)×(1,1,1)4的参数估计,从而得到模型的拟合方程为

2.4 模型的检验与诊断[14-15]
通过模型的识别与建立,笔者选择了模型 ARIMA(4,1,4)×(1,1,1)4作为最佳模型。 现在对模型 ARIMA(4,1,4)×(1,1,1)4进行残差检验,如果残差为白噪声序列,说明已经建立的模型 ARIMA(4,1,4)×(1,1,1)4包含了原始序列的所有趋势,提取了原始数据中所包含的信息,则模型通过适应性检验。如果残差序列不是白噪声序列,那么说明模型还需要改建,需要重新进行模型的识别和建立。对模型 ARIMA(4,1,4)×(1,1,1)4的残差序列进行检验,作出模型 ARIMA(4,1,4)×(1,1,1)4残差序列的自相关和偏自相关图(图10),如图所示。残差序列的各滞后阶数的自相关系数和偏自相关系数都接近于零;对残差序列进行单位根检验,检验结果如图11。检验t统计量的值为-6.542 360,小于显著性水平为1%的临界值,残差序列为白噪声序列,所以 ARIMA(4,1,4)×(1,1,1)4模型通过了残差检验,该模型可以很好的拟合时间序列的变化趋势。

图10 残差序列的自相关和偏自相关图

图11 残差序列的ADF单位根检验结果

表1 财政收入预测数值与实际数值的比较
2.5 预测
通过运用已经建立的 ARIMA (4,1,4)×(1,1,1)4模型进行预测。将预测的数值进行指数变换,即可得到2015年第一季度到2017年第三季度的财政收入季度数据的预测数值,并将预测数值与实际数值进行比较分析,结果如表1所示。同时,通过模型可以得到X时间序列的所有预测值,画出时间序列X的真实值和模型预测值的时间序列图(如图 12)。
通过对表1的观察可以发现,将2015年第一季度到2016年第三季度的预测数值与实际数值进行比较,相对误差都在 5%以内,说明模型 ARIMA(4,1,4)×(1,1,1)4的拟合效果比较好。同时,由图12可以看出X序列的真实数值和预测数值的变化趋势基本一致,预测数值与实际数值基本吻合。所以,文中建立的模型的拟合效果比较好,预测精度比较高。

图12 X序列真实值和预测值
3 结语
通过对2004年第一季度到2016年第三季度的财政收入数据进行时间序列分析,运用Eviews8.0软件进行探究财政收入趋势性和季节性的内在变化规律,建立 ARIMA 乘积季节模型 ARIMA(4,1,4)(1,1,1)4。该模型很好的拟合了财政收入季度数据时间序列的趋势性和季节性,可以在短期内预测国家的财政收入,对政府制定相应的宏观经济政策和财政政策都具有一定的参考意义。
[1]易丹辉.时间序列分析方法与应用[M].北京:中国人民大学出版社,2011:48-54.
[2]史代敏,谢小燕.应用时间序列分析[M].北京:高等教育出版社,2011:138-142.
[3]薛冬梅.ARIMA模型及其在时间序列分析中的应用[J].吉林化工学院学报,2010,27(3):80-83.
[4]王黎明,王连,杨楠.应用时间序列分析[M].上海:复旦大学出版社,2012:156-185.
[5]GEORGE E P BOX,JENKINS G M.Time Series Analysis:Forecasting and Control[M].San Francisco:Holden 2 day,2005.
[6]王燕.应用时间序列分析[M].2版.北京:中国人民大学出版社,2008.
[7]BROCKWELL P J,DAVIS R A.时间序列的理论与方法[M].田铮,译.北京:高等教育出版社,2001.
[8]何书元.应用时间序列分析[M].北京:北京大学出版社,2003.
[9]刘晓宏,金丕焕,陈启明.ARIMA模型中时间序列平稳性的统计检验方法及应用[J].中国卫生统计,1998,15(3):12-4.
[10]李嫣怡,刘荣,丁维岱.EViews统计分析与应用[M].北京:电子工业出版社,2013:295-305.
[11]樊欢欢,刘荣.Eviews统计分析与应用[M].2版.北京:机械工业出版社,2014:138-167.
[12]CHRISTODOULOS CHARISIOS,MICHALAKELIS CHRISTOS,VAROUTAS DIMITRIS.Forecasting with limited data:Combining ARIMA and diffusion models[J].Technological Forecasting and Social Change,2010,77(4):558-565.
[13]梁鑫.乘积季节模型在商品房市场中的应用研究[J].广西师范学院学报,2006,23(2):8-12.
[14]BOWERMAN B L,O'CONNELL R T.Forecasting and TimeSeries:An Applied Approach[M].3th ed.Beijing:China Ma2chine Press,2003:117-156.
[15]王振龙,胡永宏.应用时间序列分析[M].北京:科学出版社,2007.

