基于改进的PSO-SVM项目安全预测模型仿真与验证
李书全,刘世杰
(天津财经大学管理科学与工程学院,天津300222)
0 引言
近年来,基于粒子群算法优化的支持向量机(PSOSVM)在预测模型中得到了广泛应用[1,2],该模型预测误差小,精度高,具有较快的收敛速度,实现方便,适用于小样本和非线性的预测问题。建筑施工活动具有复杂性、分散性和人员流动性的特点,因此该模型比较适用于建筑施工项目的安全预测,能够取得较好的效果。传统的PSO-SVM模型在对SVM参数寻优过程中容易陷入局部最优,进而影响预测的精度[3]。鉴于此,本文以施工企业项目部为研究对象,并引入社会资本作为重要影响因素,利用粗糙集属性约简的方法辨识影响施工项目安全的要素,在此基础上将改进的粒子群算法与支持向量机相结合,建立了基于改进PSO-SVM的安全预测模型。并进行了仿真模拟,验证了该模型的有效性和实用性,为施工项目的安全预测提供科学的理论依据。
1 模型算法优化
支持向量机(SVM)是Vapnik于1995年提出来的一种计算机模型,可有效解决复杂的非线性回归问题,其基本思想是运用非线性映射将数据映射到高维特征空间里,然后在此高维特征空间对其进行线性回归[2]。粒子群(PSO)算法由Eberhart和Kenney于1995年提出的一种基于群体智能的优化算法,它是模拟鸟群随机搜寻食物的捕食行为,并从这种行为中得到启示并用于解决优化问题[1]。SVM的惩罚参数和核函数参数的选择是非常重要的问题,直接影响SVM的精度。使用传统的网格搜索方法选取SVM参数,该方法精度低且花费时间较长。将PSO应用于SVM的参数优化问题,可以得到SVM的最佳惩罚参数和核函数参数,进而可以提高施工项目安全预测模型的训练速度和准确度。但是传统PSO算法存在全局寻优能力较差,容易发生早熟收敛的问题[4]。为了解决这些问题,本文结合了惯性权重的自适应调整[5]和高斯扰动[4]的思想,对PSO算法进行了改进,在此基础上利用改进的粒子群算法(PSO)优化支持向量机(SVM)的参数,构建项目安全预测模型。改进后的PSO-SVM模型有效解决了粒子群陷入局部最优点的问题,预测精度更高,误差更小,可用于建筑施工项目安全预测模型的构建。
1.1 惯性权重的自适应调整
首先定义标准适应度(Normalized Fitness Value,NFV)的概念[5]来引导粒子更快地收敛到全局最优粒子位置。

式(1)中,fgbest为种群全局最优适应度;fmax为粒子个体的历史最大适应度;fmin为粒子个体的历史最小适应度。在此基础上,将惯性权重w定义为:
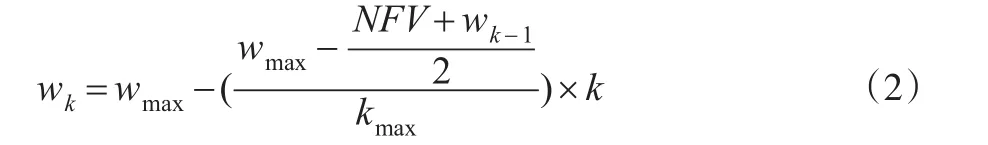
式(2)中,wk为第k次迭代中的w值,wk-1为第k-1次迭代中的w值,wmax为w的最大值,kmax为最大迭代次数。由式(2)可知,如果在第k次迭代中的NFV优于上一次迭代的值,表明该粒子所在区域存在优于全局最优值的概率较大,因此减小w的值以提高算法的局部寻优能力;反之,为了跳出当前区域,增加w的值以提高算法的全局搜索能力。这种根据适应度值调整惯性权重的方法,避免了粒子陷入局部极值点,提高了收敛速度。
1.2 高斯扰动的PSO算法
在标准PSO算法中,粒子根据如下公式来更新自己的速度和位置。

式(3)中,xid(t)为第t次迭代中粒子的位置;νid(t)为第t次迭代中粒子的速度;pid(t)和pgd(t)为第t次迭代中的粒子个体最优位置和种群全局最优位置;w为惯性权重;c1和c2为学习因子;r1和r2为[0,1]范围内均匀分布的随机数。采用高斯扰动策略,在公式(3)中,用全部粒子的含有高斯扰动项的个体最优位置总和的平均值代替pid(t)[4]。改进后的粒子速度更新公式如下所示:

式(5)中Gaussid(t)为在第t次迭代中的高斯扰动项,式(6)中Gaussian(μ,σ2)为服从高斯分布N(μ,σ2)的随机数,N为种群规模大小,r3为[0,1]范围内均匀分布的随机数。这种方法可有效增强粒子的逃逸能力,有利于粒子之间最优位置信息的共享,进而提高算法收敛精度。
2 模型仿真模拟
为了验证模型的可行性,本文参考已有研究成果的问卷调查数据,从中选取87个有效样本进行模型的仿真模拟。选取前60组样本数据作为模型的训练数据,将该60组数据中影响施工项目安全绩效的关键因素作为自变量,将项目安全绩效评价值作为因变量。然后选取另外27组样本数据作为测试数据,并使用mapminmax函数分别对训练数据及测试数据进行归一化处理。
2.1 PSO参数寻优流程
利用PSO参数寻优的流程如下:
(1)设置PSO的参数,包括种群数量sizepop、最大迭代次数maxgen、局部搜索能力参数c1、全局搜索能力参数c2、惯性权重w。
(2)产生初始粒子的位置x(i)和速度v(i)。
(3)计算初始粒子的适应度fitness(i),适应度取值为对训练集进行交叉检验时的平均均方误差(Mean Squared Error,MSE)。
(4)根据初始粒子适应度确定个体极值local_x和群体极值global_x。
(7)根据公式νid(t+1)=wνid(t)+Gaussid(t)+c2r2(pgd(t)-xid(t))更新粒子速度,根据公式xid(t+1)=xid(t)+νid(t+1)更新粒子位置。
(8)计算粒子的适应度值。
(9)将粒子的当前适应度值和个体极值比较,更新个体极值;将粒子的个体最优值和群体极值比较,更新群体极值。
(10)判断是否达到算法终止条件,即是否达到最大进化代数或小于给定精度。如果满足终止条件,算法停止运行并输出最优粒子的位置参数,即SVM的最优惩罚系数c和核函数参数g,否则转到(5)继续运行。
在算法进行初始化时,设定种群数量为20,迭代次数为100次,c1=1.5,c2=1.7,w=1。核函数参数c设定的范围为[0.1,100],参数g设定的范围为[0.01,1000][6]。PSO参数寻优的过程如图1所示。

图1 PSO寻找最佳参数的适应度曲线
从图1中可看出,参数寻优后得到的最佳参数c=18.5079,最佳参数g=0.01,最佳平均MSE=0.00041968。
2.2 回归拟合分析
本文使用MATLAB2012b和LIBSVM工具箱实现SVM模型。SVM核函数选择径向基核函数(RBF),因为无论是小样本还是大样本,高维还是低维等情况,RBF核函数均适用。在确定核函数和参数c、g后,利用LIBSVM的训练命令svmtrain对60组样本数据进行训练,得到训练模型。然后利用预测命令svmpredict对27个样本的测试数据进行回归预测,模型原始数据和回归预测数据对比图、误差图如图2所示。
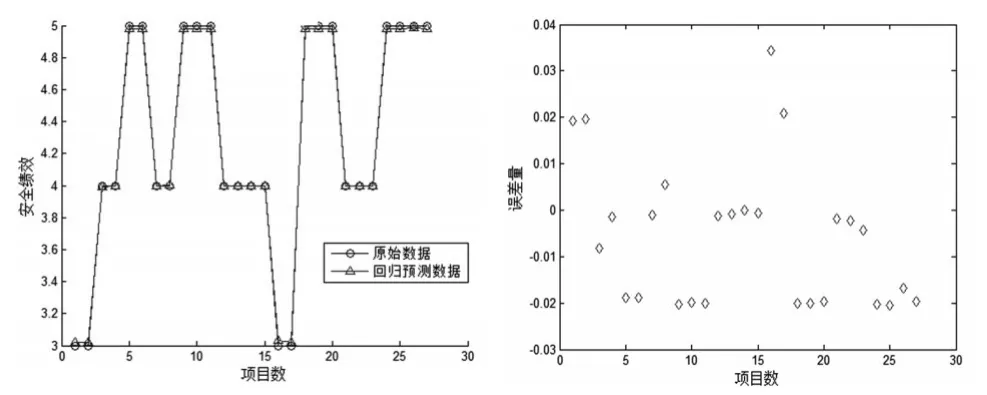
图2 改进的PSO-SVM模型仿真模拟结果
结果显示该模型预测的MSE=0.000659123,拟合相关系数=99.2974%,,绝对误差值分布在-0.03到0.04之间。结果表明本模型具有较高的预测精度,可用于施工项目安全预测建模。
3 模型验证分析
3.1 数据来源及处理
社会资本理论认为,组织或个体之间存在的信任、沟通、非正式规范等对企业绩效有积极的影响[7]。所以本文引入社会资本作为重要影响因素,从而针对建筑施工活动的特殊性做出合理的安全预测。基于安全人机工程学、安全管理学和社会资本理论,本文认为影响建筑施工安全绩效的主要因素包括:社会资本、员工安全能力、安全管理、施工设备和材料和环境条件这5个因素。本文在借鉴国内外相关文献研究[8,9]的基础上,通过现场访谈的形式确定了相对应的测量量表的维度划分。在通过专家和课题组对初始量表的讨论后,形成了本文调查的最终问卷。问卷共包括三部分内容,第一部分为项目的基本信息,第二部分为影响建筑施工项目安全绩效的因素量表,第三部分为被调查者的基本信息。题项采用李克特量表五分法,用非常不同意(1分)到非常同意(5分)来表示。本文在北京、天津、河北、河南、四川、江苏、山东等省份及直辖市进行问卷调查,调查对象包括建设施工单位的项目经理、副经理、安全经理、安全员、工长。本次问卷发放数量为360份,涉及15个省共90个项目,对无效问卷进行剔除后得到有效问卷300份,问卷有效率为83%。
采用Cronbach's α系数来检验量表的信度,结果显示各量表的Cronbach's α系数均高于0.8,量表整体的信度达到0.923,表明此项研究的量表信度值较高,具有良好的内部一致性。问卷在编制过程和多位专家进行了讨论并对题项进行了修改,可以认为量表的内容效度是可接受的。运用AMOS计算各量表的收敛效度即检验各潜在变量测量模型的适配度[10]。对各模型进行检验的结果显示:各变量测量模型的测量题项因素负荷量的C.R.值均大于1.96,各测量模型的卡方自由度比值都小于临界值3,RMESA值都小于临界值0.08,GFI值都大于临界值0.9,AGFI值都大于临界值0.9,均达到模型适配标准,表示测量模型可以与样本数据契合,说明量表具有很好的收敛效度。
ROSETTA是一种可视化很强易于操作的RS工具。将回收的300份有效问卷的结果作为RS处理的基本数据。根据RS理论将数据中的属性分为条件属性和决策属性,文中数据的条件属性即影响施工项目安全绩效的因素,共54个。决策属性即被调查者对项目安全绩效的总体评价值。首先使用ROSETTA软件中最高可信度填补法补齐原始数据中缺失的属性数据,然后采用等频率划分算法对问卷数据进行离散化处理,最后采用遗传算法对条件属性进行属性约简,最终得到35个重要因素,具体的结果如表1所示。
3.2 检验结果分析
为判断安全预测模型的有效性,本文利用前面经过RS处理过的300份样本数据,选取前200组样本数据作为模型的训练数据,然后选取另外100组样本数据作为测试数据,分别进行归一化处理。模型的参数设置如下:种群数量为20,迭代次数为200,c1=1.5,c2=1.7,w=1,核函数参数c的变化范围为[0.1,100],惩罚参数g的变化范围为[0.01,1000]。PSO参数寻优的过程如下页图3所示。

表1 影响建筑施工项目安全绩效的关键因素

图3 PSO寻找最佳参数的适应度曲线
从图3中可看出,参数寻优后得到的最佳参数c=14.6759,最佳参数g=0.01,最佳平均MSE=0.00035982。在确定核函数和参数c、g后,利用LIBSVM对200组样本数据进行训练,然后对100个样本的测试数据进行回归预测,模型原始数据和回归预测数据对比图、误差图如图4所示。
结果显示该模型预测的MSE=0.000461458,拟合相关系数=99.5853%,精度和拟合度较好。绝对误差值大多数分布在-0.03到0.03之间,误差很小。结果表明本模型具有很好的预测效果和泛化能力,也同时证明了关键因素筛选的正确性、安全预测模型的有效性和实用性。
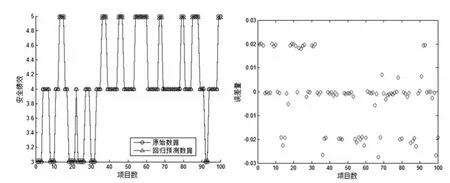
图4 改进的PSO-SVM模型验证分析结果
4 结论
(1)本文将改进的PSO算法对SVM中的参数进行优化,通过引入惯性权重的自适应调整和高斯扰动的思想,能有效解决PSO算法陷入局部最优的问题,能增强粒子的逃逸能力,可有效提高模型的训练速度和预测精度,使模型具有很好的非线性拟合能力,并减少预测误差。(2)改进的PSO-SVM模型可以有效预测建筑施工项目的总体安全绩效。模型学习速度快、预测效果好、泛化能力强、参数设置简单,在项目安全预测方面有明显的优势。实证分析的结果表明该模型具有较高的预测精度和较好的适用性,在建筑施工安全管理中有很好的应用价值。(3)社会资本是影响施工项目安全绩效的重要因素。通过调查访问,利用RS筛选出关键要素,通过对模型的仿真模拟和验证分析,检验了社会资本作为关键因素的正确性和合理性。社会资本一方面为管理者提供施工安全状况作为预测依据,另一方面为安全管理政策的执行以及形成良好的安全文化提供了无形的途径。
[1]肖智,李玲玲.PSO-SVM在高速公路交通量预测中的应用[J].管理评论,2011,23(12).
[2]吕军,王德运,魏帅.中国石油安全评价及情景预测[J].中国地质大学学报:社会科学版,2017,17(2).
[3]范振东,崔伟杰,郭芝韵等.基于改进的PSO-SVM法的大坝安全非线性预警模型研究[J].水电能源科学,2014,32(11).
[4]艾兵,董明刚.基于高斯扰动和自然选择的改进粒子群优化算法[J].计算机应用,2016,36(3).
[5]Kumar N,Vidyarthi D P.A Model for Resource-constrained Project Scheduling Using Adaptive PSO[J].Soft Computing,2016,(20).
[6]王小川,史峰,郁磊.MATLAB神经网络43个案例分析[M].北京:北京航空航天大学出版社,2013.
[7]边燕杰,丘海雄.企业的社会资本及其功效[J].中国社会科学,2000,(2).
[8]Koh T Y,Rowlinson S.Project team Social Capital,Safety Behaviors,and Performance:A Multi-level Conceptual Framework[J].Procedia Engineering,2014,(85).
[9]Cheng E W L,Ryan N,Kelly S.Exploring the Perceived Influence of Safety Management Practices on Project Performance in the Construction Industry[J].Safety Science,2012,50(2).
[10]吴明隆.结构方程模型——AMOS的操作与应用[M].重庆:重庆大学出版社,2010.

