复合Linex损失下不同先验分布中参数的Bayes估计

王敏

（贵州师范大学数学科学学院，贵阳550001）

0 引言

Linex损失是由Varian(1975)[1]提出的对称损失函数，文献[2]研究了在复合Linex对称损失下正态均值以及指数分布参数的Bayes估计问题。艾拉姆咖分布是武器装备维修理论中的常用分布，俄罗斯在研究武器装备的维修时间时引进了艾拉姆咖分布。文献[3]研究了在定数截尾场合下不同先验对艾拉姆咖分布参数估计的影响,但是该文是在平方损失下做出的估计，在平方损失中不再引入新的参数，而在复合Linex损失函数中，还需要对尺度参数α做出估计。

本文在复合Linex对称损失下，分别以伽玛分布、共轭先验以及无信息先验为艾拉姆咖参数的先验分布、得到了艾拉姆咖分布参数的唯一贝叶斯估计。通过对玛分布分布中的超参数做了灵敏性分析及对共轭先验艾拉姆咖分布中的参数给出了估计方法。并给出了艾拉姆咖分布参数的估计值，通过对比确定了一个较优的先验分布。

1 艾拉姆咖分布参数的估计

单参数艾拉姆咖分布的概率密度函数与分布函数分别为：

F(x)=1-(1+λx)e-λx,其中x＞0，且λ＞0是参数。

由式（1）易知来自艾拉姆咖总体的样本X1,X2,…,Xn的联合概率密度为：

复合Linex对称损失函数[2]形式为：

其中δ为λ的估计，a≠0是该损失函数的尺度参数。

引理1[2]：对于形状参数已知的伽玛分布，在给定尺度参数λ的先验分布π(λ)和对称损失函数（3）下，若存在估计δ，其贝叶斯风险r(δ)＜∞，则λ有唯一的贝叶斯估计：

1.1 先验分布为伽玛分布的参数估计

定理1：设x1,x2,…,xn是来自艾拉姆咖分布的一组样本观察值，参数λ的先验分布π1(λ)服从伽玛分布Γ(θ,β)，则λ具有唯一的贝叶斯估计：

证明：因为参数λ的先验分布π1(λ)服从Γ(θ,β)，则λ的密度函数为：

而样本似然函数为：

于是λ的后验密度为：

证毕。

1.2 共轭先验下的参数估计

定理2：设x1,x2,…,xn是来自艾拉姆咖分布的一组样本观察值，参数λ的先验分布π2(λ)也服从艾拉姆咖分布，则λ具有唯一的贝叶斯估计：

证明：因为参数λ的先验分布π2(λ)服从共轭先验，则λ的密度函数为：

π2(λ)=λ2αexp{-αλ}，其中α为超参数

于是λ的后验密度为：

在复合Linex损失下，λ的Bayes估计为：

证毕。

1.3 无信息先验下的参数估计

定理3：设x1,x2,…,xn是来自艾拉姆咖分布的一组样本观察值，参数λ的先验分布π3(λ)服从无信息先验，则λ具有唯一的贝叶斯估计：

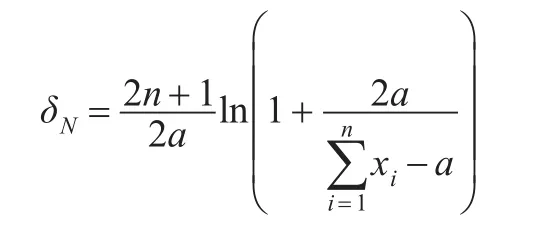
证明：参数λ的先验分布π3(λ)为无信息先验，即π3(λ)=1，于是λ的后验密度为：

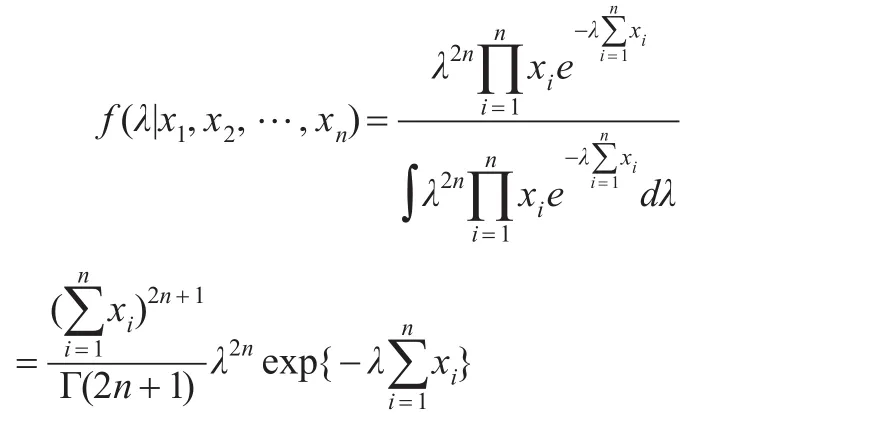
在复合Linex损失下有：

证毕。

2 先验分布中参数的估计

对于复合Linex损失中尺度参数a的估计，可以参见文献[4]中的讨论，a取正负值对参数λ的后验估计影响不大，因此本文取a=0.1。

2.1 伽玛分布中两个参数的估计

对于先验分布伽玛中的参数β与θ，取参数λ=1，样本容量为20的艾拉姆咖样本0.1586，0.4090，0.7420，1.0671，1.1866，1.3045，1.6034，1.6388，1.9408，2.0155，2.3368，2.3827，2.6109，2.7747，2.7836，2.7894，2.8058，2.8369，3.1529，3.2694.本文利用R软件，随机分别从一到十中重复取值1000次，得到β与θ的取值如下页图1所示，依次代入得到参数λ的均值为1.012044，均方差为0.08991331，由此看出参数β与θ并不灵敏，其取值对参数λ的影响不大，因此本文在后文的随机模拟中直接取β=1与θ=1。

图1

2.2 共轭艾拉姆咖分布中参数的估计

本文用极大似然法估计共轭先验中的超参数α。

用f(x|α)代替式（1），则式（2）在此时为：

取自然对数并求导得到关于α的方程：

下文随机模拟的估计中将通过R软件解式（5），得到α的估计值再代入式（4）得到λ的E-Bayes估计δα。

3 随机模拟

本文利用R软件，通过Monte-Carlo法模拟产生两组服从艾拉姆咖分布的随机样本。方法为随机抽服从均匀分布的随机变量值u，这里u～U(0,1)，再由u=F(x)=1-(1+λx)e-λx，计算出x的取值，从而得到表1。

表1 参数的Bayes估计

从表1中看出，对于λ的不同取值，各不同先验下估计都是一样精确的。对于不同的样本容量而言，样本容量越大估计越精确，在样本容量较小时，估计有一定的偏差。相比较而言，先验分布为共轭先验，即也为艾拉姆咖分布时，得到参数λ的Bayes估计最接近真值。

4 结束语

本文主要讨论的是先验分布对参数估计的影响，具体分析了在复合Linex对称损失下，对拉姆咖分布参数的先验分布为伽玛分布、共轭先验及无信息先验进行了对比，并用R语言进行了模拟分析，得出各种先验分布下分布参数的Bayes估计值，结果显示，当先验为共轭先验时，估计值最接近艾拉姆咖分布参数的真值。

[1]Varian.A Bayes Approach to Real Estate Assessment[A].Fienberg S E,ZELLENER A.Studies in Bayesian Economics and Statistics in Honour of Lenoard J.Savage[C].Amesterdam:North Holland,1975.

[2]张睿.复合Linex损失下的参数估计[D].大连:大连理工大学硕士论文,2007.

[3]龙兵.不同先验分布下艾拉姆咖分布参数的Bayes估计[J].数学的实践与认识,2015,(4).

[4]龙兵.不同损失函数下艾拉姆咖分布参数的Bayes估计——全样本情形[J].重庆师范大学学报：自然科学版,2013,(5).