极端事件的重现间隔和风险估计

张 驰，王 飞

（东南大学 经济管理学院，南京 211102）

0 引言

极端事件是指量级显著超过平均值的事件，与一般事件不同，极端事件发生的概率较低，但产生的影响巨大[1]。在很长一段时间内，极端事件通常被认为是自发性的，即相互之间互不影响。然而，越来越多的研究表明，极端事件的发生并非互相独立。相反，极端事件之间相互聚集，如气温异常、暴雨连降和金融市场中价格剧烈波动均集中在较短的时间区间内。在金融市场中，极端事件发生的频率要高于正态分布并带有复杂特征，投资者很难通过分散投资使自己保持完全对冲状态[2]。极端事件的发生也会对市场造成巨大伤害，市场动荡严重时国家经济的正常运行也会受到影响。因此，了解极端事件的特征对市场管理和风险控制都至关重要。在时间序列分析中，极端事件一直是重要的研究问题，然而，极端事件发生的低概率使得数据不足以支撑从统计学意义上对其进行研究[3]。为了解决数据不足问题，本文使用重现间隔方法进行分析。

重现间隔是指发生在两个连续极端事件之间的时间间隔。目前，重现间隔分析已被广泛应用于诸多系统的时间序列中[4-6]。近年来，大量的金融时间序列数据的产生使得能够通过重现间隔分析对金融市场的极端事件进行相对准确的分析。通过研究金融市场极端事件之间的重现间隔，能够更好地理解金融市场的波动特征和进行风险估计。从2015年开始，中国股市经历了金融危机之后不曾有过的剧烈波动，价格的大幅波动为使用重现间隔分析方法提供了大量数据，通过对数据进行分析，市场和政府可以预测此类波动是否会再次发生。因此，不同幅度波动之间的时间间隔也成为了市场和政府关心的内容。波动之间是否具有相关性，对短期和长期时间范围内的其他波动如何影响？能否通过已经发生的波动对未来波动发生的时间和幅度做出预测？波动如何帮助风险度量？通过研究波动之间的重现间隔，可以为了解中国股市提供重要的学术价值和指导意义。本文以中证500股指期货为例，研究股市的波动规律。

1 模型设计与数据描述

1.1 模型设计

重现间隔τ是指给定某一阈值q时，低于（或超过）阈值的两个连续的波动之间的等待时间。假设t时刻波动幅度大于q，由于此处q为负值，因此有R(t)＜q。则重现间隔可以表示为：

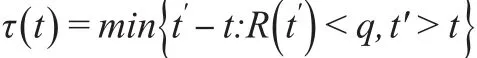
其中,t、t'代表时刻，R(t')为标准化处理过后的波动序列。重现间隔分析则是针对重现间隔τ所包含的性质进行研究的过程。

1.2 数据描述

中证500股指期货合约标的为中证指数有限公司编制和发布的中证500指数，交易代码为IC。中证500股指期货合约仿真交易自2014年3月21日开始，合约交割月份分别为交易当月起连续的两个月份，以及三月、六月、九月、十二月中两个连续的季月，共四期，同时挂牌交易。

中证500股指期货交易采用集合竞价和连续竞价两种交易方式。集合竞价时间为每个交易日9:10—9:15，其中9:10—9:14为指令申报时间，9:14—9:15为指令撮合时间。连续竞价时间为每个交易日9:15—11:30（第一节）和13:00—15:15（第二节），最后交易日连续竞价时间为9:15—11:30（第一节）和13:00—15:00（第二节）。

本文中，中证500股指期货价格数据来自于通达信数据库，样本周期始于2014年5月19日，终于2016年10月31日，去除周末以及节假日，最终样本包括97501条数据。随后对价格序列取对数并做一阶差分处理，即，其中 p(t)是在第t分钟时股指期货的价格。由于使用的是1分钟高频数据，因此∆t取1，取对数并一阶差分处理之后的时间序列见图1。图1中清晰地显示出了存在波动聚集的现象，说明存在长期相关性。其统计学特征见表1。

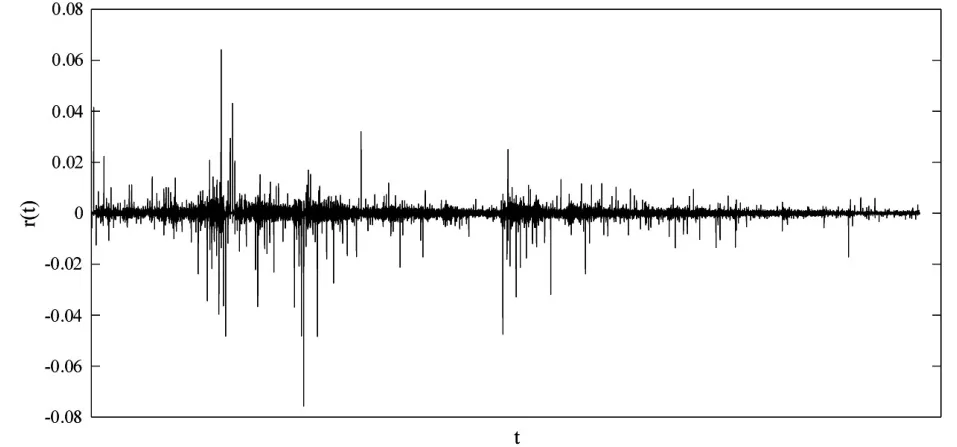
图1 中证500股指期货对数一阶差分值

表1 中证500股指期货对数一阶差分值的统计学特征

2 实证分析

2.1 经验概率分布

首先对r(t)进行标准化处理：

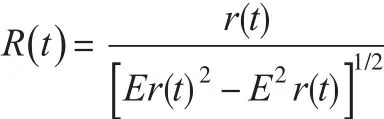
中证500股指期货波动的重现间隔的概率密度函数使用广延指数函数进行拟合[7，8]，其中是给定阈值q时的重现间隔均值，其余参数通过最大似然法进行估计，结果见表2。

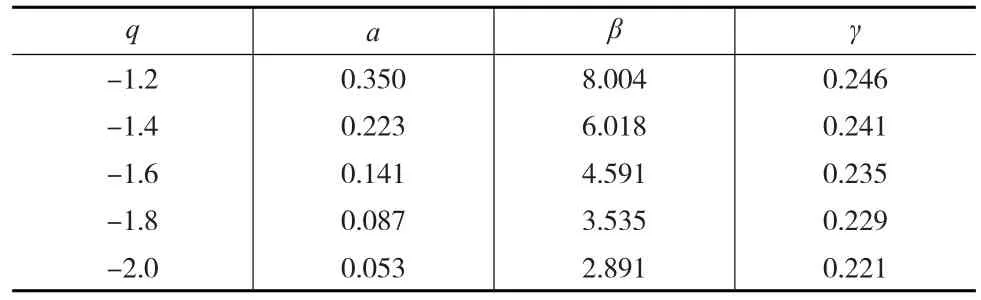
表2 拉伸式指数函数参数估计

图2显示了不同阈值q下波动重现间隔τ的经验概率分布Pq(τ)。随着阈值|q|的上升，重现间隔中长间隔的数量增加而短间隔的数量减少，这意味着愈加剧烈的波动，两次波动之间时间间隔长度更有可能增加而不是减小。从图2中还可以看出，虽然阈值不同，但每个阈值的重现间隔的概率密度函数拟合曲线却有着相似的形状。因此，重现间隔τ的概率分布函数之间是否存在可能的标度行为也就成为了本文关心的重点。

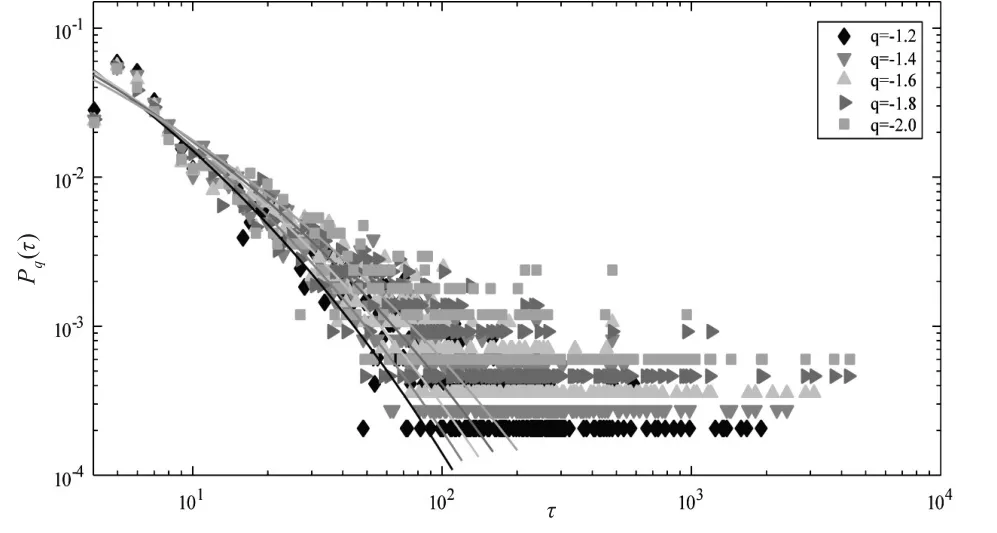
图2 中证500股指期货波动重现间隔概率密度分布

根据 Yamasaki[9]的研究，本文使用标度重现间隔 τ/进行研究，且标度重现间隔的概率分布服从其中为平均重现间隔，当阈值 q 不同时，也会随之变化，且有，说明随着波动幅度的加剧，重现间隔的平均时长也会增加，这也和事实相符。如果函数独立于 q，那么将存在单一函数 f(x)，使得对于不同的阈值q有，即标度重现间隔的概率分布会向单一曲线收敛且重现间隔具有标度行为。为了检验这一点，本文在图3中列出了作为函数的散点图。从图3中可以清楚地看出，对于不同的阈值并未向同一条曲线收敛。也说明此处重复间隔并不具有标度行为，无法通过标度处理使得可以根据小波动行为推测出大波动行为。

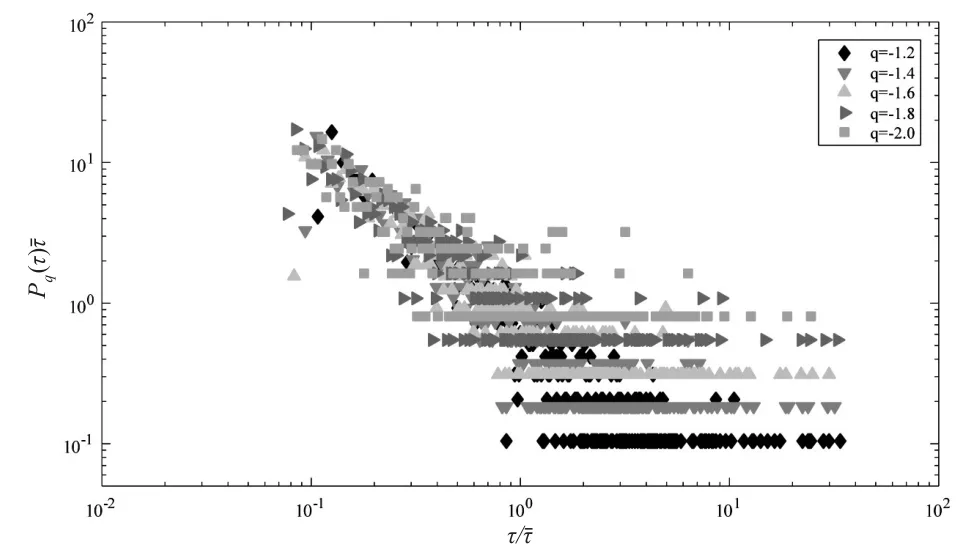
图3 中证500股指期货波动重现间隔的标度概率密度分布

2.2 记忆效应

2.2.1 短期相关性

为了研究重现间隔的短期相关性，本文首先分析条件概率密度分布函数，是指给定阈值q时，在重复间隔τ0之后出现重复间隔τ的概率。如果重现间隔中不存在短期相关性，则独立于τ0。为了得到更好的数据，本文并不选择单一数值的τ0进行研究，而是针对某一范围的τ0进行分析。

对于给定的阈值q，将其重现间隔按照递增序列进行排列，得到集合Q，将集合Q分为大小相同的四个子集，,且。则重现间隔最小的1/4集中在Q1中而最大的1/4集中在Q4。本文估计了条件概率密度函数，如果重现间隔之间不存在短期相关性，则可以得出

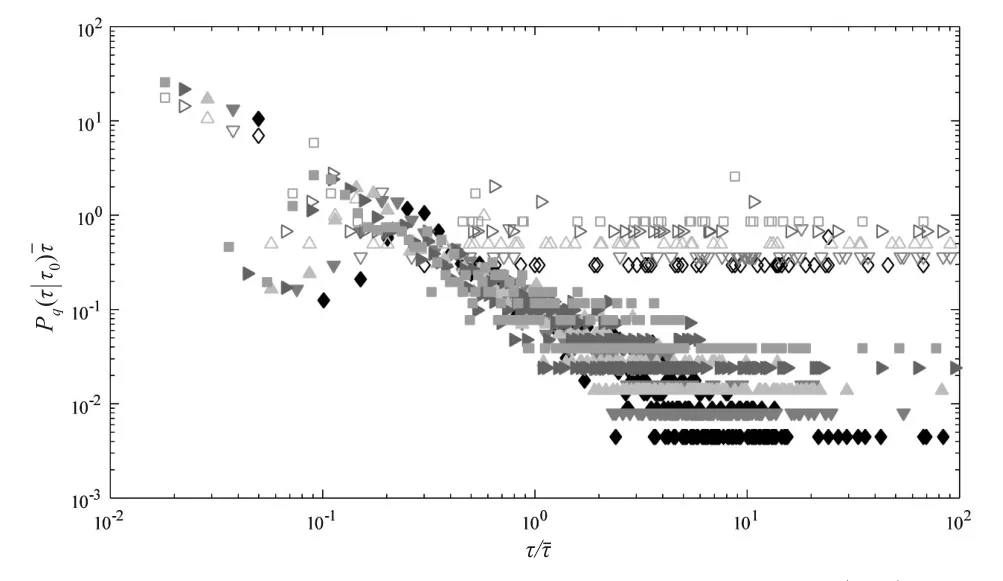
图4 中证500股指期货波动重现间隔条件概率密度函数Pq(τ|τ0)

2.2.2 长期相关性

为了研究重现间隔中可能存在的长期相关性，本文采用消除趋势波动分析法（Detrended fluctuation analysis）进行研究[10]。Chen和Hu[11,12]的研究表明，消除趋势波动分析法是检验时间序列是否存在长期相关性的有效方法。DFA通过计算消除趋势波动函数F(s)进行判别，其中s是时间单位，并且F(s)与s满足幂律关系，即F(s)～sH。H为Hurst指数，如果H＞0.5，说明序列存在长期相关性；如果H=0.5，则说明序列不存在长期相关性。图5在双对数坐标系中给出了F(s)的拟合情况，可以看出F(s)与s满足F(s)～sH关系，而Hurst指数可以通过估计拟合曲线的斜率获得，参数估计结果见表3。表3的结果显示，每一条拟合曲线的Hurst指数均大于0.5，说明重现间隔之间存在长期相关性，也证实了在中证500股指期货的高频数据中存在长期相关性。

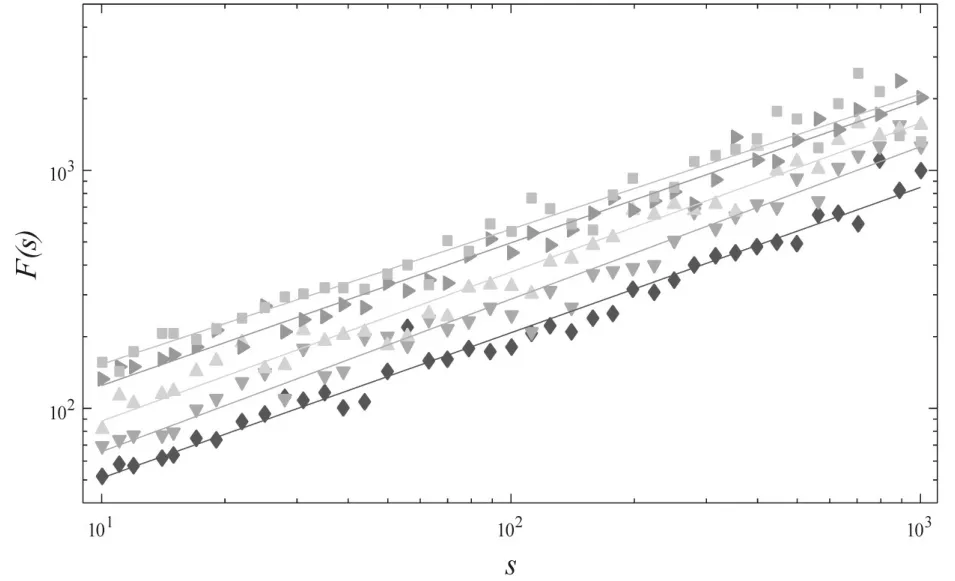
图5 消除趋势波动函数拟合情况

表3 Hurst参数估计结果

2.3 风险估计

图6显示了Wq(1|t)与t的函数关系，散点部分为实际计算值，实线部分为理论计算值。从散点部分可以看出，随着t从1增加到60时间单位内，Wq(1|t)呈缓慢下降趋势，符合之前内容和所验证的存在长期相关性这一事实。给定某一阈值q，即可计算极端事件再次发生的概率。在实线部分，可以看出当t较大时，理论值与实际值更加接近。t愈大，差异愈小，这说明风险函数Wq(∆t|t)的理论计算值在短时期内会高估风险。

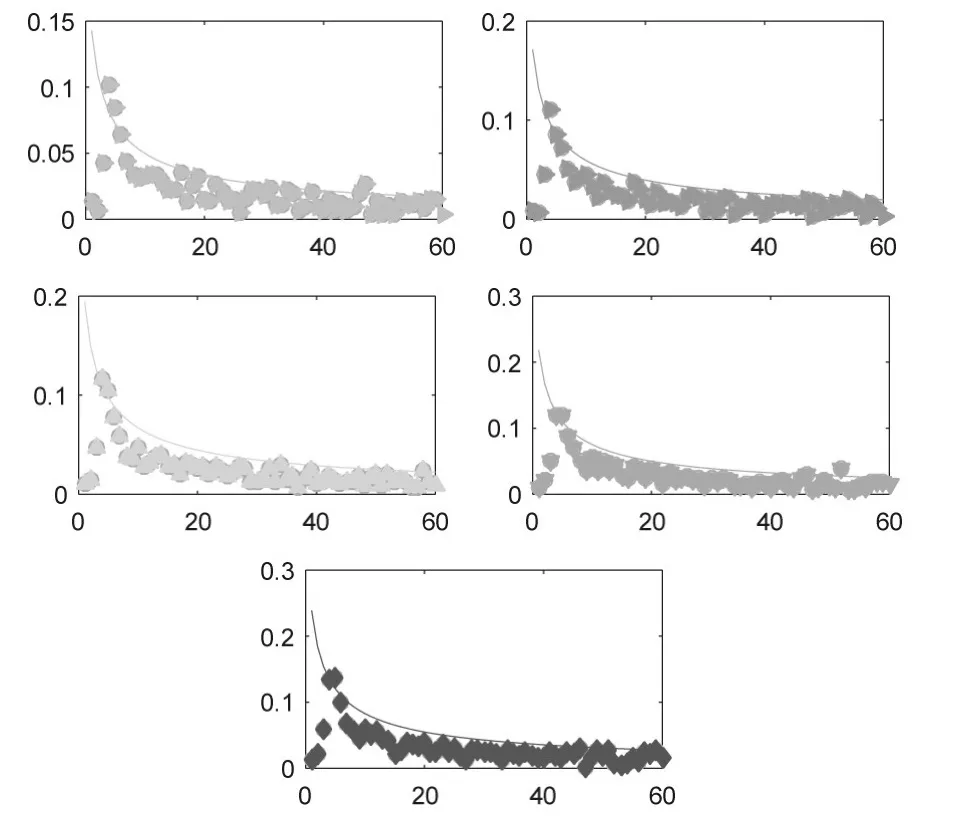
图6 Wq(1|t)理论值(实线)和实际计算值(散点标志)

在金融市场中，风险的常用指标为VaR（在险价值），因此本文使用重现间隔分析中的损失概率密度函数对VaR进行估计。VaR公式为，其中q为损失水平，P*为损失概率，P(R)是标准化序列R(t)的概率密度函数。在上文中，由于将平均重现间隔定义为，Nq是低于q的重现间隔的数量，因此约等于R(t)中的样本总数，Nq+1等于R(t)＜q样本的数量，因此可以得出平均重现间隔和VaR之间的函数关系，这意味着定义了风险水平q损失概率。图7为半对数坐标轴散点图。如果投资者想知道损失概率为1%时所对应的风险程度时，可以找到=1%所对应q值，即是所求的VaR值。

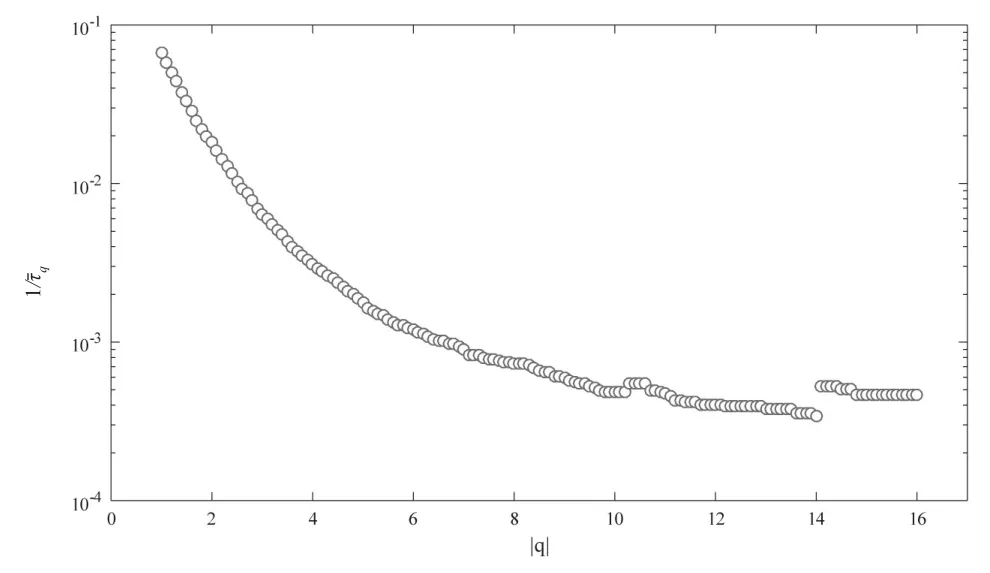
图7 中证500股指期货极端事件平均重现间隔和闭值绝对值的函数关系

3 结论

本文对中证500股指期货时间序列在低于不同阈值时，波动之间的重现间隔特征进行研究，以期进一步理解金融市场的大幅波动行为，本文主要研究了重现间隔的概率分布和记忆效应。通过研究，首先发现在不同阈值情况下，重现间隔的概率密度函数服从广延指数函数分布，但是不同阈值下概率分布函数之间不存在标度行为，无法通过标度处理以单一函数形式表示。其次，对重现间隔分别使用条件概率密度函数和消除波动趋势分析发现重现间隔之间存在短期和长期相关性，与观察到的波动之间相互集聚这一事实相符。最后，构建风险函数对中证500股指期货进行了风险估计，提供了相对准确的风险估计，风险函数Wq(∆t|t)的理论值和实际值随着时间增加愈加接近，随后建立了损失概率和VaR之间的关系。后续分析可以通过获取多个目标期货的数据进行相关性研究以及扩展样本期间继续完善，以帮助投资者更好地进行风险评估。

[1]Bogachev M I,Bunde A.Memory Effects in the Statistics of Interoc⁃currence Times Between Large Returns in Financial Records[J].Phys⁃ical Review E Statistical Nonlinear&Soft Matter Physics,2008,(78).

[2]Sornette D.Why Stock Markets Crash[M].New Jersey：Princeton Uni⁃versity Press,2009.

[3]Kotz S,Nadarajah S.Extreme Value Distributions[M].London：Imperi⁃al College Press,2000.

[4]Bunde A,Eichner J F,Kantelhardt J W,et al.Long-term Memory:A Natural Mechanism for the Clustering of Extreme Events and Anoma⁃lous Residual Times in Climate Records[J].Physical Review Letters,2005,94(4).

[5]Saichev A,Sornette D.“Universal”Distribution of Interearthquake Times Explained[J].Physical Review Letters,2006,97(7).

[6]Liu C,Jiang Z Q,Ren F,et al.Scaling and Memory in the Return In⁃tervals of Energy Dissipation Rate in Three-dimensional Fully Devel⁃oped Turbulence[J].Physical Review E Statistical Nonlinear&Soft Matter Physics,2009,80(2).

[7]Xie W J,Jiang Z Q,Zhou W X.Extreme Value Statistics and Recur⁃rence Intervals of NYMEX Energy Futures Volatility[J].Economic Modelling,2014,36(1).

[8]Suo Y Y,Wang D H,Li S P.Risk Estimation of CSI 300 Index Spot and Futures in China from a New Perspective[J].Economic Model⁃ling,2015,(49).

[9]Yamasaki K,Muchnik L,Havlin S,et al.Scaling and Memory in Vola⁃tility Return Intervals in Financial Markets[J].Proceedings of the Na⁃tional Academy of Sciences of the United States of America,2005,102(26).

[10]Peng C K,Buldyrev S V,Havlin S,et al.Mosaic organization of DNA Nucleotides[J].Physical Review E Statistical Physics Plasmas Flu⁃ids&Related Interdisciplinary Topics,1994,49(2).

[11]Chen Z,Pch I,Hu K,et al.Effect of Nonstationarities on Detrended Fluctuation Analysis[J].Physical Review E Statistical Nonlinear&Soft Matter Physics,2002,65(1).

[12]Hu K,Ivanov P C,Chen Z,et al.Effect of Trends on Detrended Fluc⁃tuation Analysis[J].Physical Review E Statistical Nonlinear&Soft Matter Physics,2001,64(1).

[13]Bogachev M I,Eichner J F,Bunde A.Effect of Nonlinear Correla⁃tions on the Statistics of Return Intervals in Multifractal Data Sets[J].Physical Review Letters,2007,99(24).